No CrossRef data available.
Article contents
THE FLOOR OF THE ARITHMETIC MEAN OF THE CUBE ROOTS OF THE FIRST 
$n$ INTEGERS
Published online by Cambridge University Press: 08 January 2020
Abstract
Zacharias [‘Proof of a conjecture of Merca on an average of square roots’, College Math. J.49 (2018), 342–345] proved Merca’s conjecture that the arithmetic means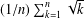 
$(1/n)\sum _{k=1}^{n}\sqrt{k}$ of the square roots of the first 
$n$ integers have the same floor values as a simple approximating sequence. We prove a similar result for the arithmetic means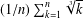 
$(1/n)\sum _{k=1}^{n}\sqrt[3]{k}$ of the cube roots of the first 
$n$ integers.
Keywords
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 261 - 267
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
The authors were supported by the Faculty of Science, Burapha University, Thailand.
References
Gould, H. W., ‘Evaluation of sums of convolved powers using Stirling and Eulerian numbers’, Fibonacci Quart. 16 (1978), 488–497.Google Scholar
Merca, M., ‘On the arithmetic mean of the square roots of the first n positive integers’, College Math. J. 48 (2017), 129–133.CrossRefGoogle Scholar
Ramanujan, S., ‘On the sum of the square roots of the first n natural numbers’, J. Indian Math. Soc. 7 (1915), 173–175.Google Scholar
Shekatkar, S., ‘The sum of the 
$r$th roots of the first $n$ natural numbers and new formula for factorial’, Preprint, 2013, arXiv:1204.0877.Google Scholar
$r$th roots of the first 
$n$ natural numbers and new formula for factorial’, Preprint, 2013, arXiv:1204.0877.Google ScholarWihler, T. P., ‘Rounding the arithmetic mean value of the square roots of the first $n$ integers’, Preprint, 2018, arXiv:1803.00362.Google Scholar
$n$ integers’, Preprint, 2018, arXiv:1803.00362.Google ScholarZacharias, J., ‘Proof of a conjecture of Merca on an average of square roots’, College Math. J. 49 (2018), 342–345.CrossRefGoogle Scholar