Published online by Cambridge University Press: 09 November 2020
For an infinite Toeplitz matrix T with nonnegative real entries we find the conditions under which the equation 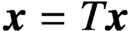 $\boldsymbol {x}=T\boldsymbol {x}$
, where
$\boldsymbol {x}=T\boldsymbol {x}$
, where 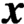 $\boldsymbol {x}$
is an infinite vector column, has a nontrivial bounded positive solution. The problem studied in this paper is associated with the asymptotic behaviour of convolution-type recurrence relations and can be applied to problems arising in the theory of stochastic processes and other areas.
$\boldsymbol {x}$
is an infinite vector column, has a nontrivial bounded positive solution. The problem studied in this paper is associated with the asymptotic behaviour of convolution-type recurrence relations and can be applied to problems arising in the theory of stochastic processes and other areas.