Published online by Cambridge University Press: 11 January 2023
Celebrating 100 years of the Banach contraction principle, we prove some fixed point theorems having all ingredients of the principle, but dealing with common fixed points of a contractive semigroup of nonlinear mappings acting in a modulated topological vector space. This research follows the ideas of the author’s recent papers [‘On modulated topological vector spaces and applications’, Bull. Aust. Math. Soc. 101 (2020), 325–332, and ‘Normal structure in modulated topological vector spaces’, Comment. Math. 60 (2020), 1–11]. Modulated topological vector spaces generalise, among others, Banach spaces and modular function spaces. The interest in modulars reflects the fact that the notions of ‘norm like’ but ‘noneuclidean’ (and not even necessarily convex) constructs to measure a level of proximity between complex objects are frequently used in science and technology. To prove our fixed point results in this setting, we introduce a new concept of Opial sets using analogies with the norm-weak and modular versions of the Opial property. As an example, the results of this work can be applied to spaces like 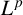 $L^p$ for
$L^p$ for 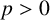 $p> 0 $, variable Lebesgue spaces
$p> 0 $, variable Lebesgue spaces 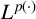 $L^{p(\cdot )}$ where
$L^{p(\cdot )}$ where  $1 \leq p(t) < + \infty $, Orlicz and Musielak–Orlicz spaces.
$1 \leq p(t) < + \infty $, Orlicz and Musielak–Orlicz spaces.