Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-16T18:48:22.135Z Has data issue: false hasContentIssue false
  • English
  • Français

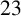$23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  23 December 2022

DAVID PENNISTON
DAVID PENNISTON*
Affiliation:
Department of Mathematics, University of Wisconsin Oshkosh, Oshkosh, WI 54901-8631, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A partition of a positive integer n is called 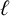$\ell $-regular if none of its parts is divisible by 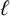$\ell $. Denote by 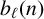$b_{\ell }(n)$ the number of 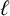$\ell $-regular partitions of n. We give a complete characterisation of the arithmetic of 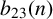$b_{23}(n)$ modulo 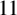$11$ for all n not divisible by 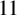$11$ in terms of binary quadratic forms. Our result is obtained by establishing a relation between the generating function for these values of 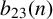$b_{23}(n)$ and certain modular forms having complex multiplication by 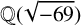${\mathbb Q}(\sqrt {-69})$.

Keywords

partitionscongruencesmodular forms

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 254 - 263
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlgren, S. and Lovejoy, J., ‘The arithmetic of partitions into distinct parts’, Mathematika 48(1–2) (2001), 203–211.10.1112/S0025579300014443CrossRefGoogle Scholar
Boll, E. and Penniston, D., ‘The $7$ -regular and $13$ -regular partition functions modulo $3$ ’, Bull. Aust. Math. Soc. 93(3) (2016), 410–419.10.1017/S0004972715001434CrossRefGoogle Scholar
Gordon, B. and Ono, K., ‘Divisibility of certain partition functions by powers of primes’, Ramanujan J. 1(1) (1997), 25–34.10.1023/A:1009711020492CrossRefGoogle Scholar
Ono, K. and Penniston, D., ‘The $2$ -adic behavior of the number of partitions into distinct parts’, J. Combin. Theory Ser. A 92(2) (2000), 138–157.10.1006/jcta.2000.3057CrossRefGoogle Scholar
Penniston, D., ‘Arithmetic of $\ell$ -regular partition functions’, Int. J. Number Theory 4(2) (2008), 295–302.10.1142/S1793042108001341CrossRefGoogle Scholar
Penniston, D., ‘ $11$ -regular partitions and a Hecke eigenform’, Int. J. Number Theory 15(6) (2019), 1251–1259.10.1142/S1793042119500696CrossRefGoogle Scholar
Serre, J.-P., ‘Sur la lacunarité des puissances de $\eta$ ’, Glasg. Math. J. 27 (1985), 203–221.10.1017/S0017089500006194CrossRefGoogle Scholar
Sturm, J., ‘On the congruence of modular forms’, in: Number Theory, Lecture Notes in Mathematics, 1240 (eds. Chudnovsky, D. V., Chudnovsky, G. V., Cohn, H. and Nathanson, M. B.) (Springer, Berlin–Heidelberg, 1984), 275–280.Google Scholar
Treneer, S., ‘Congruences for the coefficients of weakly holomorphic modular forms’, Proc. Lond. Math. Soc. (3) 93(2) (2006), 304–324.10.1112/S0024611506015814CrossRefGoogle Scholar
Webb, J. J., ‘Arithmetic of the $13$ -regular partition function modulo $3$ ’, Ramanujan J. 25(1) (2011), 49–56.10.1007/s11139-010-9227-4CrossRefGoogle Scholar