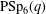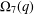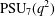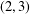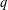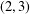Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marelli, Alessia
and
Micheloni, Rino
2016.
3D Flash Memories.
p.
281.
Chen, Yuzhu
Hu, Xun
and
Luo, Yanfeng
2016.
The finite basis property of a certain semigroup of upper triangular matrices over a field.
Journal of Algebra and Its Applications,
Vol. 15,
Issue. 09,
p.
1650177.
King, Carlisle S.H.
2017.
Generation of finite simple groups by an involution and an element of prime order.
Journal of Algebra,
Vol. 478,
Issue. ,
p.
153.
PELLEGRINI, MARCO ANTONIO
2017.
THE -GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 95,
Issue. 1,
p.
48.
Pellegrini, M.A.
and
Tamburini Bellani, M.C.
2020.
The (2,3)-generation of the finite unitary groups.
Journal of Algebra,
Vol. 549,
Issue. ,
p.
319.
Pellegrini, M.A.
and
Tamburini Bellani, M.C.
2022.
On the (2,3)-generation of the finite symplectic groups.
Journal of Algebra,
Vol. 598,
Issue. ,
p.
156.
Pellegrini, Marco Antonio
and
Tamburini Bellani, Maria Chiara
2022.
The (2, 3)-generation of the finite 8-dimensional orthogonal groups.
Journal of Group Theory,
Vol. 0,
Issue. 0,
PELLEGRINI, MARCO ANTONIO
and
TAMBURINI BELLANI, MARIA CHIARA
2024.
THE
$\boldsymbol {(2,3)}$
-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS.
Journal of the Australian Mathematical Society,
Vol. 117,
Issue. 2,
p.
130.