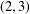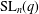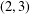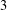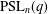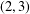Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
King, Carlisle S.H.
2017.
Generation of finite simple groups by an involution and an element of prime order.
Journal of Algebra,
Vol. 478,
Issue. ,
p.
153.
Burness, Timothy C.
2019.
Groups St Andrews 2017 in Birmingham.
p.
200.
Nuzhin, Ya. N.
2019.
Generating Sets of Involutions of Finite Simple Groups.
Algebra and Logic,
Vol. 58,
Issue. 3,
p.
288.
Pellegrini, M.A.
and
Tamburini Bellani, M.C.
2020.
The (2,3)-generation of the finite unitary groups.
Journal of Algebra,
Vol. 549,
Issue. ,
p.
319.
Boschheidgen, Jan
Klopsch, Benjamin
and
Thillaisundaram, Anitha
2020.
Generating pairs of projective special linear groups that fail to lift.
Mathematische Nachrichten,
Vol. 293,
Issue. 7,
p.
1251.
Vsemirnov, M.
and
the author
2021.
On (2,3)-generation of matrix groups over the ring of integers, II.
St. Petersburg Mathematical Journal,
Vol. 32,
Issue. 5,
p.
865.
Pellegrini, M.A.
and
Tamburini Bellani, M.C.
2022.
On the (2,3)-generation of the finite symplectic groups.
Journal of Algebra,
Vol. 598,
Issue. ,
p.
156.
Pellegrini, Marco Antonio
and
Tamburini Bellani, Maria Chiara
2022.
The (2, 3)-generation of the finite 8-dimensional orthogonal groups.
Journal of Group Theory,
Vol. 0,
Issue. 0,
Vsemirnov, M. A.
and
Nuzhin, Ya. N.
2023.
Generating Triples of Conjugate Involutions for Finite Simple Groups.
Algebra and Logic,
Vol. 62,
Issue. 5,
p.
379.
Gvozdev, R. I.
2023.
Generating Sets of Conjugate Involutions of Groups PSLn(9).
Algebra and Logic,
Vol. 62,
Issue. 4,
p.
319.
PELLEGRINI, MARCO ANTONIO
and
TAMBURINI BELLANI, MARIA CHIARA
2024.
THE
$\boldsymbol {(2,3)}$
-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS.
Journal of the Australian Mathematical Society,
Vol. 117,
Issue. 2,
p.
130.