No CrossRef data available.
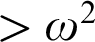 ${>}\ \omega ^2$-Fickle Recursively Enumerable Turing Degrees
${>}\ \omega ^2$-Fickle Recursively Enumerable Turing DegreesPublished online by Cambridge University Press: 28 February 2022
Given a finite lattice L that can be embedded in the recursively enumerable (r.e.) Turing degrees 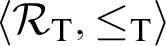 $\langle \mathcal {R}_{\mathrm {T}},\leq _{\mathrm {T}}\rangle $
, we do not in general know how to characterize the degrees
$\langle \mathcal {R}_{\mathrm {T}},\leq _{\mathrm {T}}\rangle $
, we do not in general know how to characterize the degrees 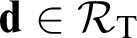 $\mathbf {d}\in \mathcal {R}_{\mathrm {T}}$
below which L can be bounded. The important characterizations known are of the
$\mathbf {d}\in \mathcal {R}_{\mathrm {T}}$
below which L can be bounded. The important characterizations known are of the 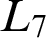 $L_7$
and
$L_7$
and 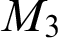 $M_3$
lattices, where the lattices are bounded below
$M_3$
lattices, where the lattices are bounded below 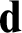 $\mathbf {d}$
if and only if
$\mathbf {d}$
if and only if 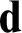 $\mathbf {d}$
contains sets of “fickleness”
$\mathbf {d}$
contains sets of “fickleness” 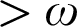 $>\omega $
and
$>\omega $
and 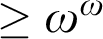 $\geq \omega ^\omega $
respectively. We work towards finding a lattice that characterizes the levels above
$\geq \omega ^\omega $
respectively. We work towards finding a lattice that characterizes the levels above 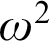 $\omega ^2$
, the first non-trivial level after
$\omega ^2$
, the first non-trivial level after  $\omega $
. We introduced a lattice-theoretic property called “
$\omega $
. We introduced a lattice-theoretic property called “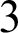 $3$
-directness” to describe lattices that are no “wider” or “taller” than
$3$
-directness” to describe lattices that are no “wider” or “taller” than 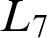 $L_7$
and
$L_7$
and 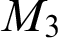 $M_3$
. We exhaust the 3-direct lattices L, but they turn out to also characterize the
$M_3$
. We exhaust the 3-direct lattices L, but they turn out to also characterize the 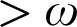 $>\omega $
or
$>\omega $
or 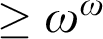 $\geq \omega ^\omega $
levels, if L is not already embeddable below all non-zero r.e. degrees. We also considered upper semilattices (USLs) by removing the bottom meet(s) of some 3-direct lattices, but the removals did not change the levels characterized. This leads us to conjecture that a USL characterizes the same r.e. degrees as the lattice on which the USL is based. We discovered three 3-direct lattices besides
$\geq \omega ^\omega $
levels, if L is not already embeddable below all non-zero r.e. degrees. We also considered upper semilattices (USLs) by removing the bottom meet(s) of some 3-direct lattices, but the removals did not change the levels characterized. This leads us to conjecture that a USL characterizes the same r.e. degrees as the lattice on which the USL is based. We discovered three 3-direct lattices besides 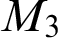 $M_3$
that also characterize the
$M_3$
that also characterize the 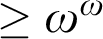 $\geq \omega ^\omega $
-levels. Our search for a
$\geq \omega ^\omega $
-levels. Our search for a 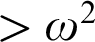 $>\omega ^2$
-candidate therefore involves the lattice-theoretic problem of finding lattices that do not contain any of the four
$>\omega ^2$
-candidate therefore involves the lattice-theoretic problem of finding lattices that do not contain any of the four 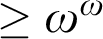 $\geq \omega ^\omega $
-lattices as sublattices.
$\geq \omega ^\omega $
-lattices as sublattices.
Abstract prepared by Liling Ko.
E-mail: [email protected]
Supervised by Peter Cholak.