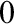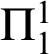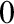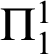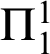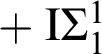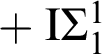1 Introduction
There are now (at least) two widespread approaches to analyzing the complexity of mathematical theorems and logical (axiomatic) systems. One is computational (recursion-theoretic) and the other is proof-theoretic. They give rise to closely related measures and hierarchies of complexity. The first grows out of recursive, computable, or constructive mathematics. Typically, we have a theorem asserting that for every object X of some kind there is another Y with specified properties. In this setting, the question one answers is how difficult (given X) is it to construct Y? The measuring rods for difficulty here are most often marked by levels of complexity with respect to computability in the sense of Turing (degrees). The second, embodied in what is now known as reverse mathematics, attempts to say how hard is it to prove the theorem. Here the measuring rods are generally axiomatic subsystems of second-order arithmetic sufficient to carry out a proof. (The standard proof-theoretically oriented text here is [Reference Simpson26]. Hirschfeldt [Reference Hirschfeldt11] gives a good view from computability theory.)
The two approaches are closely related and roughly share five basic levels of complexity that, for the first several decades of each of the two views, seemed to characterize almost all theorems of classical mathematics. Proof-theoretically, the first is a weak system of second-order arithmetic, RCA
![]() $_{0}$
which, in addition to the basic axioms about
$_{0}$
which, in addition to the basic axioms about
![]() $+$
,
$+$
,
![]() $\times $
, and
$\times $
, and
![]() $<$
, contains comprehension axioms for
$<$
, contains comprehension axioms for
![]() $\Delta _{1}^{0}$
sets and induction for
$\Delta _{1}^{0}$
sets and induction for
![]() $\Sigma _{1}^{0}$
formulas. Computationally, this corresponds to classical computable (recursive) mathematics. The other four levels are determined by adding on stronger existence/comprehension axioms. WKL
$\Sigma _{1}^{0}$
formulas. Computationally, this corresponds to classical computable (recursive) mathematics. The other four levels are determined by adding on stronger existence/comprehension axioms. WKL
![]() $_{0}$
asserts that every infinite subtree of
$_{0}$
asserts that every infinite subtree of
![]() $2^{<N}$
, the tree of finite sequences of
$2^{<N}$
, the tree of finite sequences of
![]() $0$
s and
$0$
s and
![]() $1$
s, has an (infinite) branch. The next level is ACA
$1$
s, has an (infinite) branch. The next level is ACA
![]() $_{0}$
which adds comprehension axioms for arithmetic formulas or, equivalently, requires closure under (finite iterations of) the Turing jump. The fourth level, ATR
$_{0}$
which adds comprehension axioms for arithmetic formulas or, equivalently, requires closure under (finite iterations of) the Turing jump. The fourth level, ATR
![]() $_{0}$
, extends comprehension to include transfinite iterations of arithmetic comprehension. This roughly corresponds to the transfinite iterations of the Turing jump through the recursive ordinals, i.e., the hyperarithmetic sets. The last of the basic systems is
$_{0}$
, extends comprehension to include transfinite iterations of arithmetic comprehension. This roughly corresponds to the transfinite iterations of the Turing jump through the recursive ordinals, i.e., the hyperarithmetic sets. The last of the basic systems is
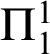 $\Pi _{1}^{1}$
-CA
$\Pi _{1}^{1}$
-CA
![]() $_{0}$
which includes comprehension for
$_{0}$
which includes comprehension for
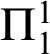 $\Pi _{1}^{1}$
formulas. This corresponds to Kleene’s hyperjump in terms of computational strength.
$\Pi _{1}^{1}$
formulas. This corresponds to Kleene’s hyperjump in terms of computational strength.
Over the past couple of decades the earlier pattern of results has been broken by a large number of constructions/theorems which are provably different from each of these “big five” systems and have unusual computational strength. They are now often called the “zoo” of reverse mathematics. (For pictures, see https://rmzoo.math.uconn.edu/diagrams/.) For ordinary theorems of classical mathematics, the large majority of these examples have been weaker than ACA
![]() $_{0}$
and so constructions recursive in a finite number of iterations of the Turing jump.
$_{0}$
and so constructions recursive in a finite number of iterations of the Turing jump.
In this communication reporting on the results in [Reference Barnes, Goh and Shore1, Reference Goh8, Reference Shore25], we discuss two related classes of mathematical theorems and logical principles that occupy neighborhoods of the reverse mathematical zoo that have had very few other denizens. They all fall outside of the big five and none are provable from ACA
![]() $_{0}$
. The first consists of what are called THAs, theorems (or theories) T of hyperarithmetical analysis (Definition 2.13). Computationally, these lie above each fixed transfinite (recursive) iteration of arithmetic comprehension but do not (proof-theoretically) imply ATR
$_{0}$
. The first consists of what are called THAs, theorems (or theories) T of hyperarithmetical analysis (Definition 2.13). Computationally, these lie above each fixed transfinite (recursive) iteration of arithmetic comprehension but do not (proof-theoretically) imply ATR
![]() $_{0}$
. While some of the THAs we study are proof-theoretically strictly weaker than ATR
$_{0}$
. While some of the THAs we study are proof-theoretically strictly weaker than ATR
![]() $_{0}$
, some are incomparable with it. Indeed, while there is a precise recursion-theoretic characterization of THAs (Definition 2.13), there can be no proof-theoretic one at least not in first-order logic. (See [Reference Van Wesep29, Theorem 2.2.2] and also [Reference Montalbán17, remarks after Definition 1.1].)
$_{0}$
, some are incomparable with it. Indeed, while there is a precise recursion-theoretic characterization of THAs (Definition 2.13), there can be no proof-theoretic one at least not in first-order logic. (See [Reference Van Wesep29, Theorem 2.2.2] and also [Reference Montalbán17, remarks after Definition 1.1].)
The study of such systems began with the work of Kreisel [Reference Kreisel15], Friedman [Reference Friedman5, Reference Friedman6, Reference Friedman7], Steel [Reference Steel28], and others in the 1960s and 1970s and continued into the last decades (as in Montalbán [Reference Montalbán17, Reference Montalbán18], Neeman [Reference Neeman20, Reference Neeman21], and others). Several axiomatic systems and logical theorems were found to be THAs and proven to lie in a number of distinct classes in terms of proof-theoretic complexity. Until now, however, there has been only one mathematical but not logical example, i.e., one not mentioning classes of first-order formulas or their syntactic complexity. This was a result (INDEC) about indecomposability of linear orderings in Jullien’s thesis [Reference Jullien13] (see [Reference Rosenstein23, Lemma 10.3]). It was shown to be a THA by Montalbán [Reference Montalbán17] and further investigated in [Reference Neeman20, Reference Neeman21].
The natural question, raised explicitly in Montalbán’s “Open Questions in Reverse Mathematics” [Reference Montalbán19, Question 30], was are there any others? The answer is provided by Barnes, Goh, and Shore [Reference Barnes, Goh and Shore1]. There is a whole family of theorems from graph-theoretic combinatorics that are THAs. The examples are primarily variations on some classical theorems of Halin [Reference Halin9, Reference Halin10] and related results in what is now called ubiquity theory. (See [Reference Diestel4, Chapter 8] for a contemporary treatment.)
The archetypical example here is what we call the Infinite Ray Theorem (IRT) from [Reference Halin9]. In more contemporary terminology, it says that any graph G which contains, for each n, a sequence
![]() $\left \langle R_{0},\ldots ,R_{n-1}\right \rangle $
of disjoint rays (a ray is a sequence
$\left \langle R_{0},\ldots ,R_{n-1}\right \rangle $
of disjoint rays (a ray is a sequence
![]() $\left \langle x_{i}|i\in N\right \rangle $
of distinct vertices such that there is an edge between each
$\left \langle x_{i}|i\in N\right \rangle $
of distinct vertices such that there is an edge between each
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{i+1}$
) also contains an infinite such sequence of rays. On its face, this sounds like a compactness theorem and so should be provable in WKL
$x_{i+1}$
) also contains an infinite such sequence of rays. On its face, this sounds like a compactness theorem and so should be provable in WKL
![]() $_{0}$
or ACA
$_{0}$
or ACA
![]() $_{0}$
. Indeed, the construction of Andreae in [Reference Diestel4, Theorem 8.2.5(i)] of the desired sequence of rays proceeds by a recursion through the natural numbers in which each step is arithmetical and so looks like a typical application of ACA
$_{0}$
. Indeed, the construction of Andreae in [Reference Diestel4, Theorem 8.2.5(i)] of the desired sequence of rays proceeds by a recursion through the natural numbers in which each step is arithmetical and so looks like a typical application of ACA
![]() $_{0}$
. We prove that it and several variations are much more complicated and indeed THAs. One collection of variations consists of consequences of a restricted version of Choice,
$_{0}$
. We prove that it and several variations are much more complicated and indeed THAs. One collection of variations consists of consequences of a restricted version of Choice,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
which is well known to be a THA (essentially [Reference Kreisel15]). The proofs that they are themselves THAs are recursion-theoretic. The analysis here led us to some related results and even a new logical system given by a restricted version of
$_{0}$
which is well known to be a THA (essentially [Reference Kreisel15]). The proofs that they are themselves THAs are recursion-theoretic. The analysis here led us to some related results and even a new logical system given by a restricted version of
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
(Definition 3.13) which is also a THA. We show by proof-theoretic arguments that another collection of variants of a version in [Reference Halin9] requiring one type of maximality of the constructed sequence which are also THAs cannot be proven in
$_{0}$
(Definition 3.13) which is also a THA. We show by proof-theoretic arguments that another collection of variants of a version in [Reference Halin9] requiring one type of maximality of the constructed sequence which are also THAs cannot be proven in
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
because each of them implies more induction than is available there. Indeed, some go beyond what is provable even in ATR
$_{0}$
because each of them implies more induction than is available there. Indeed, some go beyond what is provable even in ATR
![]() $_{0}$
. Finally we show that each of another class of variations mentioned in [Reference Halin9] that requires a different type of maximality is both proof-theoretically and computationally stronger than ATR
$_{0}$
. Finally we show that each of another class of variations mentioned in [Reference Halin9] that requires a different type of maximality is both proof-theoretically and computationally stronger than ATR
![]() $_{0}$
. Each is equivalent to
$_{0}$
. Each is equivalent to
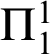 $\Pi _{1}^{1}$
-CA
$\Pi _{1}^{1}$
-CA
![]() $_{0}$
and so to closure under the hyperjump.
$_{0}$
and so to closure under the hyperjump.
We present these results in Section 3 and discuss some relations among the variations from the perspective of reverse mathematics. Almost all of these results are from [Reference Barnes, Goh and Shore1]. The technically most difficult ones that use Steel forcing to place some of these theorems (and logical systems) among the previously studied THAs with respect to proof-theoretic strength are in [Reference Goh8].
The second group of mathematical theorems and logical principles T that we study contains ones that, from the pure proof-theoretic point of view, are very weak. More precisely they are conservative over RCA
![]() $_{0}$
for a wide range of classes
$_{0}$
for a wide range of classes
![]() $\Gamma $
of sentences. (That is, for any
$\Gamma $
of sentences. (That is, for any
![]() $\varphi \in \Gamma $
, if RCA
$\varphi \in \Gamma $
, if RCA
![]() $_{0}+T\vdash \varphi $
then RCA
$_{0}+T\vdash \varphi $
then RCA
![]() $_{0}\vdash \varphi $
.) The classes
$_{0}\vdash \varphi $
.) The classes
![]() $\Gamma $
that we consider include new generalizations of the well studied one
$\Gamma $
that we consider include new generalizations of the well studied one
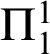 $\Pi _{1}^{1}$
and of three less studied ones,
$\Pi _{1}^{1}$
and of three less studied ones,
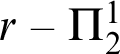 $r-\Pi_{2}^{1}$
([Reference Hirschfeldt, Shore and Slaman12]) and what we call Tanaka formulas and r-Tanaka formulas after a conjecture of Tanaka’s about the conservativity of WKL
$r-\Pi_{2}^{1}$
([Reference Hirschfeldt, Shore and Slaman12]) and what we call Tanaka formulas and r-Tanaka formulas after a conjecture of Tanaka’s about the conservativity of WKL
![]() $_{0}$
over RCA
$_{0}$
over RCA
![]() $_{0}$
proven in [Reference Simpson, Tanaka and Yamazaki27]. (See Definition 4.2.) So, in particular, none of these principles prove ACA
$_{0}$
proven in [Reference Simpson, Tanaka and Yamazaki27]. (See Definition 4.2.) So, in particular, none of these principles prove ACA
![]() $_{0}$
. On the other hand, what makes them unusual is that they each become very strong once we add ACA
$_{0}$
. On the other hand, what makes them unusual is that they each become very strong once we add ACA
![]() $_{0}$
. Many of them become THAs and these we call, ATHAs, almost theorems (theories) of hyperarithmetic analysis (Definition 2.14). These include both mathematical theorems related to the variants of Halin’s theorem and of familiar logical systems. Another collection of them forms hierarchies whose members (over ACA
$_{0}$
. Many of them become THAs and these we call, ATHAs, almost theorems (theories) of hyperarithmetic analysis (Definition 2.14). These include both mathematical theorems related to the variants of Halin’s theorem and of familiar logical systems. Another collection of them forms hierarchies whose members (over ACA
![]() $_{0}$
) prove
$_{0}$
) prove
 $\Pi _{n}^{1}$
-CA
$\Pi _{n}^{1}$
-CA
![]() $_{0}$
with n running through the natural numbers as we go up the hierarchies. At the end of these hierarchies we have principles with all these conservation properties over RCA
$_{0}$
with n running through the natural numbers as we go up the hierarchies. At the end of these hierarchies we have principles with all these conservation properties over RCA
![]() $_{0}$
which are stronger than full second-order arithmetic over ACA
$_{0}$
which are stronger than full second-order arithmetic over ACA
![]() $_{0}$
. These results are from [Reference Shore25].
$_{0}$
. These results are from [Reference Shore25].
The proofs of all of these conservativity results proceed by defining some very general classes of forcings and showing that any sentence of the desired class
![]() $\Gamma $
that can be made true in an extension of a given model of RCA
$\Gamma $
that can be made true in an extension of a given model of RCA
![]() $_{0}$
by iterating forcings from these classes must already be true in the given model. These notions of forcing include many well-known ones such as Cohen, Laver, Mathias, Sacks, and Silver forcings and many variations as well as special purpose ones introduced for specific applications to mathematical theorems related to our graph-theoretic theorems. Thus we strengthen many well-known conservativity results as well as proving new ones. The proofs (also from [Reference Shore25]) that many of these theorems are very strong over ACA
$_{0}$
by iterating forcings from these classes must already be true in the given model. These notions of forcing include many well-known ones such as Cohen, Laver, Mathias, Sacks, and Silver forcings and many variations as well as special purpose ones introduced for specific applications to mathematical theorems related to our graph-theoretic theorems. Thus we strengthen many well-known conservativity results as well as proving new ones. The proofs (also from [Reference Shore25]) that many of these theorems are very strong over ACA
![]() $_{0}$
are specific to the particular results but are usually not difficult. We view these results together as answering another question raised in [Reference Montalbán19, Section 6.1.1]. Attributing the question to Hirschfeldt, Montalbán points out that there are very few examples where natural equivalences are known to hold over strong theories but not over RCA
$_{0}$
are specific to the particular results but are usually not difficult. We view these results together as answering another question raised in [Reference Montalbán19, Section 6.1.1]. Attributing the question to Hirschfeldt, Montalbán points out that there are very few examples where natural equivalences are known to hold over strong theories but not over RCA
![]() $_{0}$
particularly if one excludes the cases where the only additional axioms needed are forms of induction. Hirschfeldt asked for more such examples. This work provides a whole array of pairs of distinct principles with a wide range of strength which are pairwise equivalent over ACA
$_{0}$
particularly if one excludes the cases where the only additional axioms needed are forms of induction. Hirschfeldt asked for more such examples. This work provides a whole array of pairs of distinct principles with a wide range of strength which are pairwise equivalent over ACA
![]() $_{0}$
but not over RCA
$_{0}$
but not over RCA
![]() $_{0}$
. Thus they provide evidence that in some settings it would make sense to take ACA
$_{0}$
. Thus they provide evidence that in some settings it would make sense to take ACA
![]() $_{0}$
as the base theory for reverse mathematical investigations rather than RCA
$_{0}$
as the base theory for reverse mathematical investigations rather than RCA
![]() $_{0}$
.
$_{0}$
.
2 Basic notions and background
2.1 Subsystems of second-order arithmetic
Formally, we are working in models
![]() $\mathcal {N}=(N,S(\mathcal {N}),+,\times ,\leq ,\in ,0,1)$
of second-order arithmetic. The first-order quantifiers range over N. The second-order ones over
$\mathcal {N}=(N,S(\mathcal {N}),+,\times ,\leq ,\in ,0,1)$
of second-order arithmetic. The first-order quantifiers range over N. The second-order ones over
![]() $S(\mathcal {N})$
which is a collection of subsets of N. The function, relations, and constants are taken to have the usual basic elementary properties. We generally abbreviate these structures as
$S(\mathcal {N})$
which is a collection of subsets of N. The function, relations, and constants are taken to have the usual basic elementary properties. We generally abbreviate these structures as
![]() $\mathcal {N}=(N,S(\mathcal {N}))$
. We are interested in ones which are models at least of RCA
$\mathcal {N}=(N,S(\mathcal {N}))$
. We are interested in ones which are models at least of RCA
![]() $_{0}$
. The standard models are those where N is
$_{0}$
. The standard models are those where N is
![]() $\mathbb {N}$
(the true natural numbers) and the remaining symbols have their standard interpretations. When we define semantics or forcing we expand the formal language to include constants for each element of N and
$\mathbb {N}$
(the true natural numbers) and the remaining symbols have their standard interpretations. When we define semantics or forcing we expand the formal language to include constants for each element of N and
![]() $S(\mathcal {N})$
and possibly some recursive (i.e.,
$S(\mathcal {N})$
and possibly some recursive (i.e.,
![]() $\boldsymbol {\Delta }_{1}^{0}$
) predicates. Unless otherwise specified, all sets and structures we consider are countable.
$\boldsymbol {\Delta }_{1}^{0}$
) predicates. Unless otherwise specified, all sets and structures we consider are countable.
The standard text here is [Reference Simpson26] to which we refer for formal details of syntax and terminology including the definitions of the basic axiom systems of reverse mathematics. The major standard axiomatic principles other than the five discussed in Section 1 that we need are variations on choice principles:
Definition 2.1.
![]() $\Sigma _{n}^{1}$
-AC is the principle
$\Sigma _{n}^{1}$
-AC is the principle
![]() $\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\Phi (A, n,Y^{[n]})]$
for every
$\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\Phi (A, n,Y^{[n]})]$
for every
![]() $\Sigma_{n}^{1}$
formula
$\Sigma_{n}^{1}$
formula
![]() $\Phi$
with free set variables A and X. In general, if Q is a principle such as this one we denote the axiomatic system RCA
$\Phi$
with free set variables A and X. In general, if Q is a principle such as this one we denote the axiomatic system RCA
![]() $_{0}+Q$
by Q
$_{0}+Q$
by Q
![]() $_{0}$
.
$_{0}$
.
2.2 Graph-theoretic notions
We take [Reference Diestel4] as our basic reference for graph theory but at times provide versions of definitions which are clearly classically equivalent to the standard ones but are better suited to reverse mathematics or complexity calculations.
Definition 2.2. A graph H is a pair
![]() $\left \langle V,E\right \rangle $
consisting of a set V (of vertices) and a set E of unordered pairs
$\left \langle V,E\right \rangle $
consisting of a set V (of vertices) and a set E of unordered pairs
![]() $\{u,v\}$
with
$\{u,v\}$
with
![]() $u\neq v$
from V (called edges). These structures are also called undirected graphs (or here U-graphs). A structure H of the form
$u\neq v$
from V (called edges). These structures are also called undirected graphs (or here U-graphs). A structure H of the form
![]() $\left \langle V,E\right \rangle $
as above is a directed graph
$\left \langle V,E\right \rangle $
as above is a directed graph
![]() $($
or here D-graph
$($
or here D-graph
![]() $)$
if E consists of ordered pairs
$)$
if E consists of ordered pairs
![]() $\left \langle u,v\right \rangle $
of vertices with
$\left \langle u,v\right \rangle $
of vertices with
![]() $u\neq v$
. To handle both cases simultaneously, we often use X to stand for undirected (U) or directed (D). We then use
$u\neq v$
. To handle both cases simultaneously, we often use X to stand for undirected (U) or directed (D). We then use
![]() $(u,v)$
to stand for the appropriate kind of edge, i.e.,
$(u,v)$
to stand for the appropriate kind of edge, i.e.,
![]() $\{u,v\}$
or
$\{u,v\}$
or
![]() $\langle u,v\rangle $
.
$\langle u,v\rangle $
.
Definition 2.3. An X-subgraph of the X-graph H is an X-graph
![]() $H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
such that
$H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
such that
![]() $V^{\prime }\subseteq V$
and
$V^{\prime }\subseteq V$
and
![]() $E^{\prime }\subseteq E$
.
$E^{\prime }\subseteq E$
.
Definition 2.4. An X-ray in H is a pair consisting of an X-subgraph
![]() $H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and an isomorphism
$H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and an isomorphism
![]() $f_{H^{\prime }}$
from N with edges
$f_{H^{\prime }}$
from N with edges
![]() $(n,n+1)$
for
$(n,n+1)$
for
![]() $n\in N$
to
$n\in N$
to
![]() $H^{\prime }$
. We say that the ray begins at
$H^{\prime }$
. We say that the ray begins at
![]() $f(0)$
. We also describe this situation by saying that H contains the X-ray
$f(0)$
. We also describe this situation by saying that H contains the X-ray
![]() $\left \langle H^{\prime },f_{H^{\prime }}\right \rangle $
. We sometimes abuse notation by saying that the sequence
$\left \langle H^{\prime },f_{H^{\prime }}\right \rangle $
. We sometimes abuse notation by saying that the sequence
![]() $\left \langle f(n)\right \rangle $
of vertices is an X-ray in H. Similarly we consider double X-rays where the isomorphism
$\left \langle f(n)\right \rangle $
of vertices is an X-ray in H. Similarly we consider double X-rays where the isomorphism
![]() $f_{H^{\prime }}$
is from the graph on
$f_{H^{\prime }}$
is from the graph on
![]() $\{\left \langle n,0\right \rangle ,\left \langle n,1\right \rangle |n\in N\}$
with edges
$\{\left \langle n,0\right \rangle ,\left \langle n,1\right \rangle |n\in N\}$
with edges
![]() $(\left \langle 0,0\right \rangle ,\left \langle 1,0\right \rangle )$
,
$(\left \langle 0,0\right \rangle ,\left \langle 1,0\right \rangle )$
,
![]() $(\left \langle n+1,0\right \rangle ,\left \langle n,0\right \rangle )$
, and
$(\left \langle n+1,0\right \rangle ,\left \langle n,0\right \rangle )$
, and
![]() $(\left \langle n,1\right \rangle ,\left \langle n+1,1\right \rangle )$
for
$(\left \langle n,1\right \rangle ,\left \langle n+1,1\right \rangle )$
for
![]() $n\in N$
, i.e., up to isomorphism the graph of the usual order relation on the integers. We use Z-ray to stand for either a (single) ray (
$n\in N$
, i.e., up to isomorphism the graph of the usual order relation on the integers. We use Z-ray to stand for either a (single) ray (
![]() $\mathrm {Z=S}$
) or double ray (
$\mathrm {Z=S}$
) or double ray (
![]() $\mathrm {Z=D}$
) and so we have, in general, Z-X-rays or just Z-rays if the type of graph (U or D) is already established.
$\mathrm {Z=D}$
) and so we have, in general, Z-X-rays or just Z-rays if the type of graph (U or D) is already established.
An X-path P in an X-graph H is defined similarly to single rays except that the domain of
![]() $f_{P}$
is a proper initial segment of N instead of N itself.
$f_{P}$
is a proper initial segment of N instead of N itself.
Definition 2.5.
H contains k many Z-X-rays for
![]() $k\in N$
if there is a sequence
$k\in N$
if there is a sequence
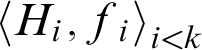 $\left \langle H_{i},f_{i}\right \rangle _{i<k}$
such that each
$\left \langle H_{i},f_{i}\right \rangle _{i<k}$
such that each
![]() $\left \langle H_{i},f_{i}\right \rangle $
is a Z-X-ray in H (with
$\left \langle H_{i},f_{i}\right \rangle $
is a Z-X-ray in H (with
![]() $H_{i}=\left \langle V_{i},E_{i}\right \rangle $
).
$H_{i}=\left \langle V_{i},E_{i}\right \rangle $
).
H contains k many disjoint (or vertex-disjoint) Z-X-rays if the
![]() $V_{i}$
are pairwise disjoint. H contains k many edge-disjoint Z-X-rays if the
$V_{i}$
are pairwise disjoint. H contains k many edge-disjoint Z-X-rays if the
![]() $E_{i}$
are pairwise disjoint. We often use Y to stand for either vertex (V) or edge (E) as in the following definitions.
$E_{i}$
are pairwise disjoint. We often use Y to stand for either vertex (V) or edge (E) as in the following definitions.
An X-graph H contains arbitrarily many Y-disjoint Z-X-rays if it contains k many such rays for every
![]() $k\in N$
.
$k\in N$
.
An X-graph H contains infinitely many Y-disjoint Z-X-rays if there is an X-subgraph
![]() $H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and a sequence
$H^{\prime }=\left \langle V^{\prime },E^{\prime }\right \rangle $
of H and a sequence
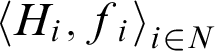 $\left \langle H_{i},f_{i}\right \rangle _{i\in N}$
such that each
$\left \langle H_{i},f_{i}\right \rangle _{i\in N}$
such that each
![]() $\left \langle H_{i},f_{i}\right \rangle $
is a Z-X-ray in H (with
$\left \langle H_{i},f_{i}\right \rangle $
is a Z-X-ray in H (with
![]() $H_{i}=\left \langle V_{i},E_{i}\right \rangle $
) such that the
$H_{i}=\left \langle V_{i},E_{i}\right \rangle $
) such that the
![]() $V_{i}$
or
$V_{i}$
or
![]() $E_{i}$
, respectively for
$E_{i}$
, respectively for
![]() $\mathrm {Y=V,E}$
, are pairwise disjoint and
$\mathrm {Y=V,E}$
, are pairwise disjoint and
![]() $V^{\prime }=\cup V_{i}$
and
$V^{\prime }=\cup V_{i}$
and
![]() $E^{\prime }=\cup E_{i}$
.
$E^{\prime }=\cup E_{i}$
.
The starting point of the work in [Reference Barnes, Goh and Shore1] is a theorem of [Reference Halin9] that we call the infinite ray theorem as expressed in [Reference Diestel4].
Definition 2.6 Halin’s Theorem
![]() $\mathrm {IRT}$
, the infinite ray theorem: Every graph H which contains arbitrarily many disjoint rays contains infinitely many.
$\mathrm {IRT}$
, the infinite ray theorem: Every graph H which contains arbitrarily many disjoint rays contains infinitely many.
We consider versions IRT
![]() $_{\mathrm {XYZ}}$
of this theorem which allow H to be an undirected (
$_{\mathrm {XYZ}}$
of this theorem which allow H to be an undirected (
![]() $\mathrm {X=U}$
) or a directed (
$\mathrm {X=U}$
) or a directed (
![]() $\mathrm {X=D}$
) graph and for the disjointness requirement to be vertex (
$\mathrm {X=D}$
) graph and for the disjointness requirement to be vertex (
![]() $\mathrm {Y=V}$
) or edge (
$\mathrm {Y=V}$
) or edge (
![]() $\mathrm {Y=E}$
). We also allow the rays to be single (
$\mathrm {Y=E}$
). We also allow the rays to be single (
![]() $\mathrm {Z=S}$
) or double (
$\mathrm {Z=S}$
) or double (
![]() $\mathrm {Z=D}$
) and consider restrictions of some of these theorems to specific families of graphs. In particular, we begin with trees. Note that we define trees as a class of graphs and so use in our basic language for our definitions the edge relation but not the induced partial order. This causes some conflict between the standard graph-theoretic terminology above and some common set-theoretic terminology. For example, a path in a tree (viewed as a graph) need not start at the root of the tree or be linearly ordered in the induced partial order on the tree. We define the branches of a tree so that they are actually the maximal linearly ordered sets in the tree with respect to the usual induced ordering as is fairly common in set-theoretic terminology.
$\mathrm {Z=D}$
) and consider restrictions of some of these theorems to specific families of graphs. In particular, we begin with trees. Note that we define trees as a class of graphs and so use in our basic language for our definitions the edge relation but not the induced partial order. This causes some conflict between the standard graph-theoretic terminology above and some common set-theoretic terminology. For example, a path in a tree (viewed as a graph) need not start at the root of the tree or be linearly ordered in the induced partial order on the tree. We define the branches of a tree so that they are actually the maximal linearly ordered sets in the tree with respect to the usual induced ordering as is fairly common in set-theoretic terminology.
Definition 2.7. A tree is a graph T with a designated element r called its root such that for each vertex
![]() $v\neq r$
there is a unique path from r to v. A branch in T is a ray that begins at its root. We denote the set of its branches by
$v\neq r$
there is a unique path from r to v. A branch in T is a ray that begins at its root. We denote the set of its branches by
![]() $[T]$
and say that T is well-founded if
$[T]$
and say that T is well-founded if
![]() $[T]=\emptyset $
and otherwise it is ill-founded. A forest is an effective disjoint union of trees, or more formally, a graph with a designated set R (of vertices called roots) such that for each vertex v there is a unique
$[T]=\emptyset $
and otherwise it is ill-founded. A forest is an effective disjoint union of trees, or more formally, a graph with a designated set R (of vertices called roots) such that for each vertex v there is a unique
![]() $r\in R$
such that there is a path from r to v and, moreover, there is only one such path. In general, the effectiveness we assume when we take disjoint unions of graphs means that we can effectively (i.e., computably) identify each vertex in the union with the original vertex (and the graph to which it belongs) which it represents in the disjoint union.
$r\in R$
such that there is a path from r to v and, moreover, there is only one such path. In general, the effectiveness we assume when we take disjoint unions of graphs means that we can effectively (i.e., computably) identify each vertex in the union with the original vertex (and the graph to which it belongs) which it represents in the disjoint union.
Definition 2.8. A directed tree is a directed graph
![]() $T=\left \langle V,E\right \rangle $
such that its underlying graph
$T=\left \langle V,E\right \rangle $
such that its underlying graph
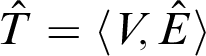 $\hat {T}=\langle V,\hat {E}\rangle $
where
$\hat {T}=\langle V,\hat {E}\rangle $
where
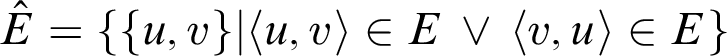 $\hat {E}=\{\{u,v\}|\langle u,v\rangle \in E\,\vee \,\langle v,u\rangle \in E\}$
is a tree. A directed forest is a directed graph whose underlying graph is a forest.
$\hat {E}=\{\{u,v\}|\langle u,v\rangle \in E\,\vee \,\langle v,u\rangle \in E\}$
is a tree. A directed forest is a directed graph whose underlying graph is a forest.
Definition 2.9. An X-graph H is locally finite if, for each
![]() $u\in V$
, the set
$u\in V$
, the set
![]() $\{v\in E|(u,v)\in E\,\vee \,(v,u)\in E\}$
of neighbors of u is finite.
$\{v\in E|(u,v)\in E\,\vee \,(v,u)\in E\}$
of neighbors of u is finite.
2.3 The hyperarithmetic hierarchy
We assume familiarity with the basic notion of relative complexity of sets and functions as given by Turing reducibility,
![]() $X \ \leq _{T}Y$
, and the Turing jump operator,
$X \ \leq _{T}Y$
, and the Turing jump operator,
![]() $X^{\prime }$
, and refer to any standard text such as [Reference Rogers22]. Iterating the jump into the transfinite brings us to hyperarithmetic theory. Here, the now standard text is [Reference Sacks24].
$X^{\prime }$
, and refer to any standard text such as [Reference Rogers22]. Iterating the jump into the transfinite brings us to hyperarithmetic theory. Here, the now standard text is [Reference Sacks24].
Definition 2.10. We represent ordinals
![]() $\alpha $
as well-ordered relations on N. Typically such ordinal notations are endowed with various additional structures such as identifying
$\alpha $
as well-ordered relations on N. Typically such ordinal notations are endowed with various additional structures such as identifying
![]() $0$
, successor, and limit ordinals and specifying cofinal
$0$
, successor, and limit ordinals and specifying cofinal
![]() $\omega $
-sequences for the limit ordinals. An ordinal is recursive (in a set X) if it has a recursive (in X) representation. For a set X and ordinal (notation)
$\omega $
-sequences for the limit ordinals. An ordinal is recursive (in a set X) if it has a recursive (in X) representation. For a set X and ordinal (notation)
![]() $\alpha $
recursive in X, we define the transfinite iterations
$\alpha $
recursive in X, we define the transfinite iterations
![]() $X^{(\alpha )}$
of the Turing jump of X by induction:
$X^{(\alpha )}$
of the Turing jump of X by induction:
![]() $X^{(0)}=X$
;
$X^{(0)}=X$
;
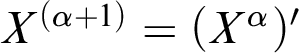 $X^{(\alpha +1)}=(X^{\alpha })^{\prime }$
; and for a limit ordinal
$X^{(\alpha +1)}=(X^{\alpha })^{\prime }$
; and for a limit ordinal
![]() $\lambda $
,
$\lambda $
,
 $X^{(\lambda )}=\oplus \{X^{(\alpha )}|\alpha <\lambda \}$
(or as the sum over the
$X^{(\lambda )}=\oplus \{X^{(\alpha )}|\alpha <\lambda \}$
(or as the sum over the
![]() $X^{(\alpha )}$
in the specified cofinal sequence).
$X^{(\alpha )}$
in the specified cofinal sequence).
Definition 2.11.
![]() $HY\!P(X)$
, the collection of all sets hyperarithmetic in X consists of those sets recursive in some
$HY\!P(X)$
, the collection of all sets hyperarithmetic in X consists of those sets recursive in some
![]() $X^{(\alpha )}$
for
$X^{(\alpha )}$
for
![]() $\alpha $
an ordinal recursive in X. These are also the sets
$\alpha $
an ordinal recursive in X. These are also the sets
![]() $\Delta _{1}^{1}$
in X.
$\Delta _{1}^{1}$
in X.
Above all the sets hyperarithmetic in X lies its hyperjump.
Definition 2.12. The hyperjump of X,
![]() $\mathcal {O}^{X}$
, is the set
$\mathcal {O}^{X}$
, is the set
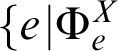 $\{e|\Phi _{e}^{X}$
is (the characteristic function of) a well-founded subtree of
$\{e|\Phi _{e}^{X}$
is (the characteristic function of) a well-founded subtree of
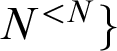 $N^{<N}\}$
.
$N^{<N}\}$
.
We can now define the primary objects of our analysis. Note that the definitions only refer to standard models.
Definition 2.13. A sentence (theory) T is a theorem
![]() $($
theory
$($
theory
![]() $)$
of hyperarithmetic analysis
$)$
of hyperarithmetic analysis
![]() $($
THA
$($
THA
![]() $)$
if
$)$
if
-
1. For every
 $X\subseteq \mathbb {N}$
,
$X\subseteq \mathbb {N}$
,
 $(\mathbb {N},HY\!P(X))\vDash T$
and
$(\mathbb {N},HY\!P(X))\vDash T$
and -
2. For every
 $S\subseteq 2^{\mathbb {N}}$
, if
$S\subseteq 2^{\mathbb {N}}$
, if
 $(\mathbb {N},S)\vDash T$
and
$(\mathbb {N},S)\vDash T$
and
 $X\in S$
then
$X\in S$
then
 $HY\!P(X)\subseteq S$
.
$HY\!P(X)\subseteq S$
.
Definition 2.14. A theorem or theory T is an almost theorem
![]() $($
theory
$($
theory
![]() $)$
of hyperarithmetic analysis
$)$
of hyperarithmetic analysis
![]() $($
ATHA
$($
ATHA
![]() $)$
, if
$)$
, if
![]() $T\nvdash \mathrm {ACA}_{0}$
but
$T\nvdash \mathrm {ACA}_{0}$
but
![]() $T+\mathrm {ACA}_{0}$
is a THA.
$T+\mathrm {ACA}_{0}$
is a THA.
3 IRT
 $_{\mathrm {XYZ}}$
and hyperarithmetic analysis
$_{\mathrm {XYZ}}$
and hyperarithmetic analysis
We analyze the strength of the variations
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
of Halin’s theorem. Classically,
$\mathrm {IRT}_{\mathrm {XYZ}}$
of Halin’s theorem. Classically,
![]() $\mathrm {IRT}_{\mathrm {UVS}}$
and
$\mathrm {IRT}_{\mathrm {UVS}}$
and
![]() $\mathrm {IRT}_{\mathrm {UVD}}$
were proved by Halin [Reference Halin9, Reference Halin10].
$\mathrm {IRT}_{\mathrm {UVD}}$
were proved by Halin [Reference Halin9, Reference Halin10].
![]() $\mathrm {IRT}_{\mathrm {UES}}$
is an exercise in [Reference Diestel4, Theorem 8.2.5(ii)] while
$\mathrm {IRT}_{\mathrm {UES}}$
is an exercise in [Reference Diestel4, Theorem 8.2.5(ii)] while
![]() $\mathrm {IRT}_{\mathrm {DVS}}$
and
$\mathrm {IRT}_{\mathrm {DVS}}$
and
![]() $\mathrm {IRT}_{\mathrm {DES}}$
may be folklore. We prove that all of these are THAs. Of the other three variants,
$\mathrm {IRT}_{\mathrm {DES}}$
may be folklore. We prove that all of these are THAs. Of the other three variants,
![]() $\mathrm {IRT}_{\mathrm {DED}}$
and
$\mathrm {IRT}_{\mathrm {DED}}$
and
![]() $\mathrm {IRT}_{\mathrm {DVD}}$
are open problems of graph theory ([Reference Bowler, Carmesin and Pott2] and Bowler (personal communication)). We do, however, have interesting and unusual results about these principles when restricted to directed forests. The remaining variant,
$\mathrm {IRT}_{\mathrm {DVD}}$
are open problems of graph theory ([Reference Bowler, Carmesin and Pott2] and Bowler (personal communication)). We do, however, have interesting and unusual results about these principles when restricted to directed forests. The remaining variant,
![]() $\mathrm {IRT}_{\mathrm {UED}}$
, was proved by Bowler, Carmesin and Pott [Reference Bowler, Carmesin and Pott2] using structural results about the topological notion of ends in graphs. All the results in this section not otherwise attributed are from [Reference Barnes, Goh and Shore1].
$\mathrm {IRT}_{\mathrm {UED}}$
, was proved by Bowler, Carmesin and Pott [Reference Bowler, Carmesin and Pott2] using structural results about the topological notion of ends in graphs. All the results in this section not otherwise attributed are from [Reference Barnes, Goh and Shore1].
We first note some reverse mathematical relations among these principles.
Theorem 3.1 RCA
 $_{0}$
$_{0}$
-
(i)
 $\mathrm {IRT}_{\mathrm {DED}}\rightarrow \mathrm {IRT}_{\mathrm {DVD}}$
,
$\mathrm {IRT}_{\mathrm {DED}}\rightarrow \mathrm {IRT}_{\mathrm {DVD}}$
,
 $\mathrm {IRT}_{\mathrm {UED}}$
,
$\mathrm {IRT}_{\mathrm {UED}}$
,
 $\mathrm {IRT}_{\mathrm {DES}}$
.
$\mathrm {IRT}_{\mathrm {DES}}$
. -
(ii)
 $\mathrm {IRT}_{\mathrm {DVD}}\rightarrow \mathrm {IRT}_{\mathrm {UVD}}$
,
$\mathrm {IRT}_{\mathrm {DVD}}\rightarrow \mathrm {IRT}_{\mathrm {UVD}}$
,
 $\mathrm {IRT}_{\mathrm {DVS}}$
.
$\mathrm {IRT}_{\mathrm {DVS}}$
. -
(iii)
 $\mathrm {IRT}_{\mathrm {DES}}\rightarrow \mathrm {IRT}_{\mathrm {DVS}}$
,
$\mathrm {IRT}_{\mathrm {DES}}\rightarrow \mathrm {IRT}_{\mathrm {DVS}}$
,
 $\mathrm {IRT}_{\mathrm {UES}}$
.
$\mathrm {IRT}_{\mathrm {UES}}$
. -
(iv)
 $\mathrm {IRT}_{\mathrm {DVS}}\rightarrow \mathrm {IRT}_{\mathrm {UVS}}$
.
$\mathrm {IRT}_{\mathrm {DVS}}\rightarrow \mathrm {IRT}_{\mathrm {UVS}}$
.
The proofs of these implications are purely combinatorial and all follow the same basic plan. To deduce
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
from
$\mathrm {IRT}_{\mathrm {XYZ}}$
from
![]() $\mathrm {IRT} _{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
we provide computable maps g, h, and k which take X-graphs G to X
$\mathrm {IRT} _{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
we provide computable maps g, h, and k which take X-graphs G to X
![]() ${}^{\prime }$
-graphs
${}^{\prime }$
-graphs
![]() $G^{\prime }$
, Y-disjoint Z-rays or sets of Y-disjoint Z-rays in G to Y
$G^{\prime }$
, Y-disjoint Z-rays or sets of Y-disjoint Z-rays in G to Y
![]() ${}^{\prime } $
-disjoint Z
${}^{\prime } $
-disjoint Z
![]() ${}^{\prime }$
-rays or sets of Y
${}^{\prime }$
-rays or sets of Y
![]() ${}^{\prime }$
-disjoint Z
${}^{\prime }$
-disjoint Z
![]() ${}^{\prime }$
-rays in
${}^{\prime }$
-rays in
![]() $G^{\prime }$
, and Y
$G^{\prime }$
, and Y
![]() ${}^{\prime }$
-disjoint Z
${}^{\prime }$
-disjoint Z
![]() ${}^{\prime } $
-rays or sets of Y
${}^{\prime } $
-rays or sets of Y
![]() ${}^{\prime }$
-disjoint Z
${}^{\prime }$
-disjoint Z
![]() ${}^{\prime }$
-rays in
${}^{\prime }$
-rays in
![]() $G^{\prime }$
to Y-disjoint Z-rays or sets of Y-disjoint Z-rays in G, respectively. These functions are designed to take witnesses of the hypothesis of
$G^{\prime }$
to Y-disjoint Z-rays or sets of Y-disjoint Z-rays in G, respectively. These functions are designed to take witnesses of the hypothesis of
![]() $\mathrm {IRT} _{\mathrm {XYZ}}$
in G to witnesses of the hypothesis of
$\mathrm {IRT} _{\mathrm {XYZ}}$
in G to witnesses of the hypothesis of
![]() $\mathrm {IRT} _{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
in
$\mathrm {IRT} _{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
in
![]() $G^{\prime }$
and witnesses to the conclusion of
$G^{\prime }$
and witnesses to the conclusion of
![]() $\mathrm {IRT}_{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
in
$\mathrm {IRT}_{\mathrm {X^{\prime }Y^{\prime }Z^{\prime }}}$
in
![]() $G^{\prime }$
to witnesses to the conclusion of
$G^{\prime }$
to witnesses to the conclusion of
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
in G. Clearly it suffices to provide such computable maps to establish the desired reduction in
$\mathrm {IRT}_{\mathrm {XYZ}}$
in G. Clearly it suffices to provide such computable maps to establish the desired reduction in
![]() $\mathrm {RCA}_{0}$
. We use these reductions to prove one of our major results: all of the
$\mathrm {RCA}_{0}$
. We use these reductions to prove one of our major results: all of the
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
have strength at least that of some THAs and that most are, in fact, themselves THAs. We discuss two other reductions not in RCA
$\mathrm {IRT}_{\mathrm {XYZ}}$
have strength at least that of some THAs and that most are, in fact, themselves THAs. We discuss two other reductions not in RCA
![]() $_{0}$
in Theorem 3.10 and Section 4.
$_{0}$
in Theorem 3.10 and Section 4.
Theorem 3.2. All single-ray variants of
![]() $\ \mathrm {IRT}\ ($
i.e.,
$\ \mathrm {IRT}\ ($
i.e.,
![]() $\mathrm {IRT}_{\mathrm {XYS}})$
and
$\mathrm {IRT}_{\mathrm {XYS}})$
and
![]() $\mathrm {IRT}_{\mathrm {UVD}}$
are theorems of hyperarithmetic analysis.
$\mathrm {IRT}_{\mathrm {UVD}}$
are theorems of hyperarithmetic analysis.
The proofs have two parts. One is recursion-theoretic. It first provides a coding into computable graphs that have arbitrarily many disjoint rays such that any sequence of infinitely many disjoint rays computes
![]() $0^{\prime }$
. Thus each of the principles implies ACA
$0^{\prime }$
. Thus each of the principles implies ACA
![]() $_{0}$
. Then we prove that, if
$_{0}$
. Then we prove that, if
![]() $0^{(\alpha )}$
exists for each
$0^{(\alpha )}$
exists for each
![]() $\alpha <\lambda $
(recursive ordinals), then
$\alpha <\lambda $
(recursive ordinals), then
![]() $0^{(\lambda )}$
exists. The method here is to use known facts of hyperarithmetic theory to construct a sequence of trees each of which has exactly one branch uniformly of degree
$0^{(\lambda )}$
exists. The method here is to use known facts of hyperarithmetic theory to construct a sequence of trees each of which has exactly one branch uniformly of degree
![]() $0^{(\alpha )}$
(or variations appropriate to the version of IRT being considered) and apply the version of IRT to get a sequence of these branches cofinal in
$0^{(\alpha )}$
(or variations appropriate to the version of IRT being considered) and apply the version of IRT to get a sequence of these branches cofinal in
![]() $\lambda $
and so construct
$\lambda $
and so construct
![]() $0^{(\lambda )}$
. This guarantees that the second clause of the definition of THA (2.13) is satisfied.
$0^{(\lambda )}$
. This guarantees that the second clause of the definition of THA (2.13) is satisfied.
The second part consists of showing that each of these versions of IRT is provable from the THA
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
. Thus the IRT variants satisfy the first clause as well. The proofs of the variants in
$_{0}$
. Thus the IRT variants satisfy the first clause as well. The proofs of the variants in
![]() $\Sigma _{1}^{1} $
-AC
$\Sigma _{1}^{1} $
-AC
![]() $_{0}$
are mostly careful analyses of standard proofs or variations on such. The basic constructions are recursions which at each step perform arithmetic operations on given or constructed graphs and apply Menger’s theorem for finite graphs. The construction for IRT
$_{0}$
are mostly careful analyses of standard proofs or variations on such. The basic constructions are recursions which at each step perform arithmetic operations on given or constructed graphs and apply Menger’s theorem for finite graphs. The construction for IRT
![]() $_{\mathrm {DES}}$
requires some additional ideas that include using line graphs to move from edge disjointness to vertex disjointness and a reduction to locally finite graphs similar to an analysis in [Reference Bowler, Carmesin and Pott2] that we discuss in Section 4.
$_{\mathrm {DES}}$
requires some additional ideas that include using line graphs to move from edge disjointness to vertex disjointness and a reduction to locally finite graphs similar to an analysis in [Reference Bowler, Carmesin and Pott2] that we discuss in Section 4.
What prevents the construction from being one in ACA
![]() $_{0}$
is the need to apply the hypothesis of IRT at step n to be able to use a sequence
$_{0}$
is the need to apply the hypothesis of IRT at step n to be able to use a sequence
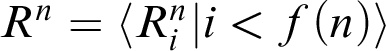 $R^{n}=\left \langle R_{i}^{n}|i<f(n)\right \rangle $
of disjoint rays of length
$R^{n}=\left \langle R_{i}^{n}|i<f(n)\right \rangle $
of disjoint rays of length
![]() $f(n)$
for some specified recursive function f. While the hypothesis tells us there is such a sequence for each n, producing the whole sequence
$f(n)$
for some specified recursive function f. While the hypothesis tells us there is such a sequence for each n, producing the whole sequence
![]() $\left \langle R^{n}\right \rangle $
to start the constructions formally seems to use some form of choice (
$\left \langle R^{n}\right \rangle $
to start the constructions formally seems to use some form of choice (
![]() $\Sigma _{1}^{1}$
-AC clearly suffices). This preliminary step is the essential source of the complexity of the IRT
$\Sigma _{1}^{1}$
-AC clearly suffices). This preliminary step is the essential source of the complexity of the IRT
![]() $_{\mathrm {XYZ}}$
. Indeed, we show that, each IRT
$_{\mathrm {XYZ}}$
. Indeed, we show that, each IRT
![]() $_{\mathrm {XYS}}$
and IRT
$_{\mathrm {XYS}}$
and IRT
![]() $_{\mathrm {UVD}}$
is equivalent (over RCA
$_{\mathrm {UVD}}$
is equivalent (over RCA
![]() $_{0}$
) to the principle that its hypothesis implies the existence of a sequence
$_{0}$
) to the principle that its hypothesis implies the existence of a sequence
![]() $\left \langle R^{n} \right \rangle $
as just described.
$\left \langle R^{n} \right \rangle $
as just described.
Definition 3.3.
![]() $\mathrm {SCR}_{\mathrm {XYZ}}$
: For every X-graph G with arbitrarily many Y-disjoint Z-rays, there is a sequence
$\mathrm {SCR}_{\mathrm {XYZ}}$
: For every X-graph G with arbitrarily many Y-disjoint Z-rays, there is a sequence
![]() $\langle R^{n} \rangle $
such that each
$\langle R^{n} \rangle $
such that each
![]() $R^{n}$
is a sequence of n many Y-disjoint Z-rays.
$R^{n}$
is a sequence of n many Y-disjoint Z-rays.
We now turn to two other types of variations on IRT that involve notions of maximality. The first actually follows the original formulation of IRT in [Reference Halin9].
Definition 3.4.
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
: Every X-graph G has a set of Y-disjoint Z-rays of maximum cardinality.
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
: Every X-graph G has a set of Y-disjoint Z-rays of maximum cardinality.
It is easy to see that the difference between
![]() $\mathrm {IRT}_{\mathrm {XYZ} }^{\ast }$
and
$\mathrm {IRT}_{\mathrm {XYZ} }^{\ast }$
and
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
is just an induction argument. It suffices to have I
$\mathrm {IRT}_{\mathrm {XYZ}}$
is just an induction argument. It suffices to have I
![]() $\Sigma _{1}^{1}$
, induction for
$\Sigma _{1}^{1}$
, induction for
![]() $\Sigma _{1}^{1}$
(rather than
$\Sigma _{1}^{1}$
(rather than
![]() $\Sigma _{1}^{0}$
) formulas.
$\Sigma _{1}^{0}$
) formulas.
Proposition 3.5. For each choice of XYZ,
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
over
$\mathrm {IRT}_{\mathrm {XYZ}}$
over
![]() $\mathrm {RCA}_{0}$
and
$\mathrm {RCA}_{0}$
and
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
implies
$\mathrm {IRT}_{\mathrm {XYZ}}$
implies
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
over
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
over
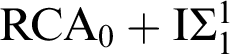 $\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
. Therefore
$\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
. Therefore
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
and
$\mathrm {IRT}_{\mathrm {XYZ}}$
and
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
are equivalent over
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
are equivalent over
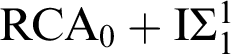 $\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
$\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
As a theory being a THA depends only on its standard models (in which full induction holds), we see that we have another collection of THAs from the literature.
Theorem 3.6. For all the
![]() $\mathrm {IRT}_{\mathrm {XYS}}$
and
$\mathrm {IRT}_{\mathrm {XYS}}$
and
![]() $\mathrm {IRT}_{\mathrm {UVD}} \ ($
which are THAs by Theorem 3.2
$\mathrm {IRT}_{\mathrm {UVD}} \ ($
which are THAs by Theorem 3.2
![]() $)$
, the
$)$
, the
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
are also THAs.
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
are also THAs.
Moreover, we can show that these IRT
![]() $_{\mathrm {XYZ}}^{\ast }$
are proof-theoretically strictly stronger than the corresponding IRT
$_{\mathrm {XYZ}}^{\ast }$
are proof-theoretically strictly stronger than the corresponding IRT
![]() $_{\mathrm {XYZ}}$
and indeed not even provable from
$_{\mathrm {XYZ}}$
and indeed not even provable from
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
.
$_{0}$
.
Theorem 3.7. For each choice of XYZ,
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
![]() $\mathrm {ACA}_{0}^{\ast }$
and so proves the consistency of
$\mathrm {ACA}_{0}^{\ast }$
and so proves the consistency of
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
. Thus none is provable in
$\mathrm {AC}_{0}$
. Thus none is provable in
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
. In particular
$\mathrm {AC}_{0}$
. In particular
![]() $\mathrm {IRT}_{\mathrm {XYS}}$
and
$\mathrm {IRT}_{\mathrm {XYS}}$
and
![]() $\mathrm {IRT}_{\mathrm {UVD}}$
are each strictly weaker than the corresponding
$\mathrm {IRT}_{\mathrm {UVD}}$
are each strictly weaker than the corresponding
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
Here ACA
![]() $_{0}^{\ast }$
is the known principle adding the instance of induction giving all finite iterations of the jump:
$_{0}^{\ast }$
is the known principle adding the instance of induction giving all finite iterations of the jump:
 ${(\forall A)(\forall n)(\exists W)(W^{[0]}=A\wedge (\forall i<n)}(W^{[i+1]}=W^{[i]^{\prime }}))$
. The proof of Theorem 3.7 shows first that ACA
${(\forall A)(\forall n)(\exists W)(W^{[0]}=A\wedge (\forall i<n)}(W^{[i+1]}=W^{[i]^{\prime }}))$
. The proof of Theorem 3.7 shows first that ACA
![]() $_{0}^{\ast }$
follows from each IRT
$_{0}^{\ast }$
follows from each IRT
![]() $_{\mathrm {XYZ}}^{\ast }$
by using [Reference Simpson26, Lemma V.5.4] and then examining the argument for [Reference Simpson26, Corollary IX.4.6] to get the consistency result.
$_{\mathrm {XYZ}}^{\ast }$
by using [Reference Simpson26, Lemma V.5.4] and then examining the argument for [Reference Simpson26, Corollary IX.4.6] to get the consistency result.
We can do more for special cases of the open questions IRT
![]() $_{\mathrm {DED}}$
and IRT
$_{\mathrm {DED}}$
and IRT
![]() $_{\mathrm {DVD}}$
. Indeed, we have that restricting these principles to various classes of graphs supplies new THAs which are strictly stronger than
$_{\mathrm {DVD}}$
. Indeed, we have that restricting these principles to various classes of graphs supplies new THAs which are strictly stronger than
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
and not provable even in
$\mathrm {AC}_{0}$
and not provable even in
![]() $\mathrm {ATR}_{0}$
.
$\mathrm {ATR}_{0}$
.
Theorem 3.8. Each of
![]() $\mathrm {IRT}_{\mathrm {DYD}}^{\ast }$
restricted to directed forests is a THA which strictly implies
$\mathrm {IRT}_{\mathrm {DYD}}^{\ast }$
restricted to directed forests is a THA which strictly implies
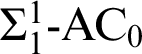 $\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
$\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
![]() $\mathrm {RCA}_{0}$
but is not provable in
$\mathrm {RCA}_{0}$
but is not provable in
![]() $\mathrm {ATR}_{0}$
.
$\mathrm {ATR}_{0}$
.
More generally, we can precisely characterize the reverse mathematical strength of all these variants.
Theorem 3.9. The following are equivalent
![]() $($
over
$($
over
![]() $\mathrm {RCA}_{0})\!:$
$\mathrm {RCA}_{0})\!:$
-
1.
 $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
 $\mathrm {AC}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
$\mathrm {AC}_{0}+\mathrm {I}\Sigma _{1}^{1}$
. -
2.
 $\mathrm {IRT}_{\mathrm {DED}}\ {}$
for directed forests
$\mathrm {IRT}_{\mathrm {DED}}\ {}$
for directed forests
 ${}+\mathrm {I}\Sigma _{1}^{1} $
.
${}+\mathrm {I}\Sigma _{1}^{1} $
. -
3.
 $\mathrm {IRT}_{\mathrm {DED}}^{\ast }\ {}$
for directed forests.
$\mathrm {IRT}_{\mathrm {DED}}^{\ast }\ {}$
for directed forests. -
4.
 $\mathrm {IRT}_{\mathrm {DVD}}^{\ast }\ {}$
for directed forests.
$\mathrm {IRT}_{\mathrm {DVD}}^{\ast }\ {}$
for directed forests. -
5.
 $\mathrm {IRT}_{\mathrm {DVD}}\ {}$
for directed forests
$\mathrm {IRT}_{\mathrm {DVD}}\ {}$
for directed forests
 ${}+\mathrm {I}\Sigma _{1}^{1} $
.
${}+\mathrm {I}\Sigma _{1}^{1} $
.
The proofs here use a new combinatorial argument to show that
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
implies
$\mathrm {AC}_{0}$
implies
![]() $\mathrm {IRT}_{\mathrm {DED}}$
for directed forests, a short coding to derive
$\mathrm {IRT}_{\mathrm {DED}}$
for directed forests, a short coding to derive
![]() $\Sigma _{1}^{1}$
-AC from IRT
$\Sigma _{1}^{1}$
-AC from IRT
![]() $_{\mathrm {DVD} }^{\ast }$
and another one to show that IRT
$_{\mathrm {DVD} }^{\ast }$
and another one to show that IRT
![]() $_{\mathrm {DVD}}^{\ast }$
implies I
$_{\mathrm {DVD}}^{\ast }$
implies I
![]() $\Sigma _{1}^{1}$
as well as several previously established implications. As I
$\Sigma _{1}^{1}$
as well as several previously established implications. As I
![]() $\Sigma _{1}^{1}$
is not provable in ATR
$\Sigma _{1}^{1}$
is not provable in ATR
![]() $_{0}$
by [Reference Simpson26, Corollary IX.4.7], we have a lower bound for IRT
$_{0}$
by [Reference Simpson26, Corollary IX.4.7], we have a lower bound for IRT
![]() $_{\mathrm {DYD}}^{\ast }$
.
$_{\mathrm {DYD}}^{\ast }$
.
More difficult combinatorial arguments show that if we consider IRT
![]() $_{\mathrm {UVD}}^{\ast }$
over RCA
$_{\mathrm {UVD}}^{\ast }$
over RCA
![]() $_{0}$
and so IRT
$_{0}$
and so IRT
![]() $_{\mathrm {UVD}}$
over RCA
$_{\mathrm {UVD}}$
over RCA
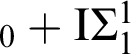 $_{0}+\mathrm {I}\Sigma _{1}^{1}$
we can derive a reduction not implied by those of Theorem 3.1 and the immediate ones of Proposition 3.5.
$_{0}+\mathrm {I}\Sigma _{1}^{1}$
we can derive a reduction not implied by those of Theorem 3.1 and the immediate ones of Proposition 3.5.
Theorem 3.10.
![]() $\mathrm {IRT}_{\mathrm {UVD}}^{\ast }$
implies
$\mathrm {IRT}_{\mathrm {UVD}}^{\ast }$
implies
![]() $\mathrm {IRT}_{\mathrm {UVS}}$
over
$\mathrm {IRT}_{\mathrm {UVS}}$
over
![]() $\mathrm {RCA}_{0}$
. Therefore
$\mathrm {RCA}_{0}$
. Therefore
![]() $\ (1) \ \mathrm {IRT}_{\mathrm {UVD}}$
implies
$\ (1) \ \mathrm {IRT}_{\mathrm {UVD}}$
implies
![]() $\mathrm {IRT}_{\mathrm {UVS}}$
over
$\mathrm {IRT}_{\mathrm {UVS}}$
over
 $\mathrm {RCA}_{0} + \mathrm {I}\Sigma _{1}^{1};$
and
$\mathrm {RCA}_{0} + \mathrm {I}\Sigma _{1}^{1};$
and
![]() $($
2
$($
2
![]() $)$
if any standard model of
$)$
if any standard model of
![]() $\mathrm {RCA}_{0}$
satisfies
$\mathrm {RCA}_{0}$
satisfies
![]() $\mathrm {IRT}_{\mathrm {UVD}}$
, then it satisfies
$\mathrm {IRT}_{\mathrm {UVD}}$
, then it satisfies
![]() $\mathrm {IRT}_{\mathrm {UVS}}$
as well.
$\mathrm {IRT}_{\mathrm {UVS}}$
as well.
We now turn to the second notion of maximality for IRT variants. Instead of asking for sets of disjoint rays of maximal cardinality we ask for ones that are maximal in the sense of containment. Of course, the existence of such sets follows immediately from Zorn’s Lemma and was so noted in [Reference Halin9]. In terms of computational and reverse mathematical strength, they are much stronger than the IRT or IRT
![]() $^{\ast }$
versions.
$^{\ast }$
versions.
Definition 3.11.
![]() $\mathrm {MIRT}_{\mathrm {XYZ}}$
: Every X-graph G has a (possibly finite) sequence
$\mathrm {MIRT}_{\mathrm {XYZ}}$
: Every X-graph G has a (possibly finite) sequence
![]() $(R_{i})_{i}$
of Y-disjoint Z-rays which is maximal, i.e., for any Z-ray R in G, there is some i such that R and
$(R_{i})_{i}$
of Y-disjoint Z-rays which is maximal, i.e., for any Z-ray R in G, there is some i such that R and
![]() $R_{i}$
are not Y-disjoint.
$R_{i}$
are not Y-disjoint.
Theorem 3.12. Each
![]() $\mathrm {MIRT}_{\mathrm {XYZ}}$
is equivalent to
$\mathrm {MIRT}_{\mathrm {XYZ}}$
is equivalent to
![]() $\Pi _{1}^{1}$
-
$\Pi _{1}^{1}$
-
![]() $\mathrm {CA}_{0}$
over
$\mathrm {CA}_{0}$
over
![]() $\mathrm {RCA}_{0}$
.
$\mathrm {RCA}_{0}$
.
We close this section with a summary of the relations between the THAs introduced here along with another new one that they suggested and others already studied in the literature. Many of our results are displayed in Figure 1.

Figure 1 Partial zoo involving known axiom systems and some IRT variants. Single arrows denote implication over
![]() $\mathrm {RCA}_{0}$
while double arrows denote strict implication over
$\mathrm {RCA}_{0}$
while double arrows denote strict implication over
![]() $\mathrm {RCA}_{0}$
. All theories are THA except for
$\mathrm {RCA}_{0}$
. All theories are THA except for
![]() $\mathrm {MIRT}$
,
$\mathrm {MIRT}$
,
![]() $\Pi ^{1}_{1}$
-
$\Pi ^{1}_{1}$
-
![]() $\mathrm {CA}_{0}$
,
$\mathrm {CA}_{0}$
,
![]() $\mathrm {ATR}_{0}$
, and
$\mathrm {ATR}_{0}$
, and
![]() $\mathrm {ACA}_{0}$
: For the IRT variants see Theorems 3.2 and 3.6; otherwise see [Reference Montalbán17]. For readability we have not displayed all variants of
$\mathrm {ACA}_{0}$
: For the IRT variants see Theorems 3.2 and 3.6; otherwise see [Reference Montalbán17]. For readability we have not displayed all variants of
![]() $\mathrm {IRT}_{}$
and
$\mathrm {IRT}_{}$
and
![]() $\mathrm {IRT}^{\ast }_{}$
. Most of the results in the figure are proved for some other
$\mathrm {IRT}^{\ast }_{}$
. Most of the results in the figure are proved for some other
![]() $\mathrm {IRT} _{\mathrm {XYZ}}$
as well (or
$\mathrm {IRT} _{\mathrm {XYZ}}$
as well (or
![]() $\mathrm {IRT}^{\ast }_{\mathrm {XYZ}}$
, as appropriate) except for (4). The unlabeled implications and nonimplications along and to the right of the vertical axis from
$\mathrm {IRT}^{\ast }_{\mathrm {XYZ}}$
, as appropriate) except for (4). The unlabeled implications and nonimplications along and to the right of the vertical axis from
![]() $\Pi ^{1}_{1}$
-
$\Pi ^{1}_{1}$
-
![]() $\mathrm {CA} _{0}$
to
$\mathrm {CA} _{0}$
to
![]() $\mathrm {ACA}_{0}$
are well-known (see [Reference Simpson26], in particular Corollary IX.4.7). (1): These are proved in [Reference Goh8]. The implications from
$\mathrm {ACA}_{0}$
are well-known (see [Reference Simpson26], in particular Corollary IX.4.7). (1): These are proved in [Reference Goh8]. The implications from
![]() $\Sigma ^{1}_{1}$
-
$\Sigma ^{1}_{1}$
-
![]() $\mathrm {AC}_{0}$
to
$\mathrm {AC}_{0}$
to
![]() $\mathrm {IRT}_{\mathrm {DES}}$
and
$\mathrm {IRT}_{\mathrm {DES}}$
and
![]() $\mathrm {IRT}_{\mathrm {UVD}}$
follow from our proof of Theorem 3.2 (see the second paragraph after Theorem 3.2). The implications from
$\mathrm {IRT}_{\mathrm {UVD}}$
follow from our proof of Theorem 3.2 (see the second paragraph after Theorem 3.2). The implications from
![]() $\Sigma ^{1}_{1}$
-
$\Sigma ^{1}_{1}$
-
 $\mathrm {AC}_{0} + \mathrm {I}\Sigma ^{1}_{1}$
to
$\mathrm {AC}_{0} + \mathrm {I}\Sigma ^{1}_{1}$
to
![]() $\mathrm {IRT}^{\ast }_{\mathrm {DES}}$
and
$\mathrm {IRT}^{\ast }_{\mathrm {DES}}$
and
![]() $\mathrm {IRT}^{\ast }_{\mathrm {UVD}}$
follow from the above and Proposition 3.5. The strict implications from
$\mathrm {IRT}^{\ast }_{\mathrm {UVD}}$
follow from the above and Proposition 3.5. The strict implications from
![]() $\mathrm {IRT}^{\ast }_{\mathrm {XYZ}}$
to
$\mathrm {IRT}^{\ast }_{\mathrm {XYZ}}$
to
![]() $\mathrm {IRT} _{\mathrm {XYZ}}$
hold by Proposition 3.5 and Theorem 3.7. (2): Theorems 3.14 and 3.7. (3): Theorem 3.1. (4): Theorem 3.10; strictness follows from Theorem 3.7. The strict implications (5) follow from our proof of Theorem 3.2 (see the first paragraph after Theorem 3.2). (6): Theorem 3.12. (7): Theorem 3.9 (the subscript DF indicates that we restrict
$\mathrm {IRT} _{\mathrm {XYZ}}$
hold by Proposition 3.5 and Theorem 3.7. (2): Theorems 3.14 and 3.7. (3): Theorem 3.1. (4): Theorem 3.10; strictness follows from Theorem 3.7. The strict implications (5) follow from our proof of Theorem 3.2 (see the first paragraph after Theorem 3.2). (6): Theorem 3.12. (7): Theorem 3.9 (the subscript DF indicates that we restrict
![]() $\mathrm {IRT}^{\ast }_{\mathrm {DED}}$
to directed forests).
$\mathrm {IRT}^{\ast }_{\mathrm {DED}}$
to directed forests).
As mentioned in Section 1, the only previously known purely mathematical THA was INDEC. There were also one or two quasi-mathematical ones which, like ABW, are versions of standard principles such as the Bolzano–Weierstrass theorem but restricted to arithmetic sets of reals. (See [Reference Friedman7] and [Reference Conidis3].) All the others were typical logical axioms or theorems. The standard examples include
![]() $\Sigma _{1}^{1}$
-DC
$\Sigma _{1}^{1}$
-DC
![]() $_{0}$
,
$_{0}$
,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0} $
,
$_{0} $
,
![]() $\Delta _{1}^{1}$
-CA
$\Delta _{1}^{1}$
-CA
![]() $_{0}$
, as well as
$_{0}$
, as well as
![]() $\Pi _{1}^{1}$
-SEP and weak-
$\Pi _{1}^{1}$
-SEP and weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
. The known relationships among these systems were as follows:
$_{0}$
. The known relationships among these systems were as follows:
![]() $\Sigma _{1}^{1}$
-DC
$\Sigma _{1}^{1}$
-DC
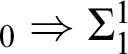 $_{0}\Rightarrow \Sigma _{1}^{1}$
-AC
$_{0}\Rightarrow \Sigma _{1}^{1}$
-AC
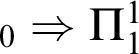 $_{0} \Rightarrow \Pi _{1}^{1}$
-SEP
$_{0} \Rightarrow \Pi _{1}^{1}$
-SEP
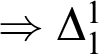 $\Rightarrow \Delta _{1}^{1}$
-CA
$\Rightarrow \Delta _{1}^{1}$
-CA
![]() $_{0}\Rightarrow $
INDEC
$_{0}\Rightarrow $
INDEC
![]() $_{0}$
;
$_{0}$
;
![]() $\Delta _{1}^{1}$
-CA
$\Delta _{1}^{1}$
-CA
![]() $_{0}\Rightarrow $
weak-
$_{0}\Rightarrow $
weak-
![]() $\Sigma _{1}^{1} $
-AC
$\Sigma _{1}^{1} $
-AC
![]() $_{0}$
;
$_{0}$
;
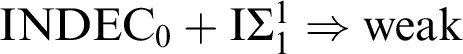 $\mathrm {INDEC}_{0}+\mathrm {I}\Sigma _{1}^{1}\Rightarrow \mathrm {weak}$
-
$\mathrm {INDEC}_{0}+\mathrm {I}\Sigma _{1}^{1}\Rightarrow \mathrm {weak}$
-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0} $
;
$_{0} $
;
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
 $_{0} +\mathrm {I}\Sigma _{1}^{1}\Rightarrow $
ABW
$_{0} +\mathrm {I}\Sigma _{1}^{1}\Rightarrow $
ABW
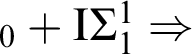 $_{0}+\mathrm {I}\Sigma _{1} ^{1}\Rightarrow $
weak-
$_{0}+\mathrm {I}\Sigma _{1} ^{1}\Rightarrow $
weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
; and
$_{0}$
; and
![]() $\Delta _{1}^{1}$
-CA
$\Delta _{1}^{1}$
-CA
![]() $_{0}\nvdash $
ABW
$_{0}\nvdash $
ABW
![]() $_{0}\nvdash $
INDEC
$_{0}\nvdash $
INDEC
![]() $_{0}$
. We use
$_{0}$
. We use
![]() $\Rightarrow $
to denote strict implication between theories. (See [Reference Conidis3, Reference Montalbán17, Reference Montalbán18, Reference Neeman20, Reference Simpson26] for definitions, proofs, and references.)
$\Rightarrow $
to denote strict implication between theories. (See [Reference Conidis3, Reference Montalbán17, Reference Montalbán18, Reference Neeman20, Reference Simpson26] for definitions, proofs, and references.)
We have already provided many relations between
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
and IRT
$\mathrm {AC}_{0}$
and IRT
![]() $_{\mathrm {XYZ}}^{\ast }$
and IRT
$_{\mathrm {XYZ}}^{\ast }$
and IRT
![]() $_{\mathrm {XYZ}}$
. Our first step in providing consequences of the IRT
$_{\mathrm {XYZ}}$
. Our first step in providing consequences of the IRT
![]() $_{\mathrm {XYZ}}^{\ast }$
or IRT
$_{\mathrm {XYZ}}^{\ast }$
or IRT
![]() $_{\mathrm {XYZ}}$
which we know are implied by
$_{\mathrm {XYZ}}$
which we know are implied by
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
 $_{0}+\mathrm {I}\Sigma _{1}^{1}$
or
$_{0}+\mathrm {I}\Sigma _{1}^{1}$
or
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
, respectively, was that weak-
$_{0}$
, respectively, was that weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
follows from
$_{0}$
follows from
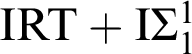 $\mathrm {IRT} +\mathrm {I}\Sigma _{1}^{1}$
. This proof led us to an apparent strengthening of weak-
$\mathrm {IRT} +\mathrm {I}\Sigma _{1}^{1}$
. This proof led us to an apparent strengthening of weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
which was also a consequence of each IRT
$_{0}$
which was also a consequence of each IRT
![]() $_{\mathrm {XYZ}}^{\ast }$
.
$_{\mathrm {XYZ}}^{\ast }$
.
Definition 3.13. The principle finite-
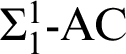 $\Sigma _{1}^{1}\text {-}\mathrm {AC}$
asserts that, for every arithmetic
$\Sigma _{1}^{1}\text {-}\mathrm {AC}$
asserts that, for every arithmetic
![]() $\Phi (A,n,X)$
,
$\Phi (A,n,X)$
,
 $$\begin{align*}\forall A[(\forall n)(\exists\text{ nonzero finitely many }X)\Phi (A,n,X)\rightarrow\exists Y\forall n\Phi(A,n,Y^{[n]})]\text{.} \end{align*}$$
$$\begin{align*}\forall A[(\forall n)(\exists\text{ nonzero finitely many }X)\Phi (A,n,X)\rightarrow\exists Y\forall n\Phi(A,n,Y^{[n]})]\text{.} \end{align*}$$
Here we have weakened the usual hypothesis of weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
from asserting that for each n there is precisely one X such that
$_{0}$
from asserting that for each n there is precisely one X such that
![]() $A(n,X) $
to there being a finite sequence containing all such X. So, of course, finite-
$A(n,X) $
to there being a finite sequence containing all such X. So, of course, finite-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
implies weak-
$_{0}$
implies weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
. We provide many other relations as well.
$_{0}$
. We provide many other relations as well.
Theorem 3.14.
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies finite-
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies finite-
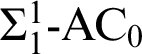 $\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
$\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
![]() $\mathrm {RCA}_{0}$
. So
$\mathrm {RCA}_{0}$
. So
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
implies finite-
$\mathrm {IRT}_{\mathrm {XYZ}}$
implies finite-
 $\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
$\Sigma _{1}^{1}\text {-}\mathrm {AC}_{0}$
over
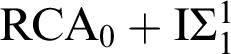 $\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
$\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
Theorem 3.15.
![]() $\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
$\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
implies
![]() $\mathrm {ABW}_{0}$
over
$\mathrm {ABW}_{0}$
over
![]() $\mathrm {RCA}_{0}$
. Therefore
$\mathrm {RCA}_{0}$
. Therefore
![]() $\mathrm {IRT}_{\mathrm {XYZ}}$
implies
$\mathrm {IRT}_{\mathrm {XYZ}}$
implies
![]() $\mathrm {ABW}_{0}$
over
$\mathrm {ABW}_{0}$
over
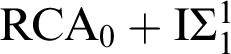 $\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
$\mathrm {RCA}_{0}+\mathrm {I}\Sigma _{1}^{1}$
.
Theorem 3.16.
![]() $\Delta _{1}^{1}$
-
$\Delta _{1}^{1}$
-
![]() $\mathrm {CA}_{0}\nvdash \mathrm {IRT}_{\mathrm {XYZ}},\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
$\mathrm {CA}_{0}\nvdash \mathrm {IRT}_{\mathrm {XYZ}},\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
Theorem 3.17.
![]() $\mathrm {ABW}_{0}\nvdash \mathrm {IRT}_{\mathrm {XYZ}},\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
$\mathrm {ABW}_{0}\nvdash \mathrm {IRT}_{\mathrm {XYZ}},\mathrm {IRT}_{\mathrm {XYZ}}^{\ast }$
.
These nonimplication results use previously known models. Goh [Reference Goh8] proves an additional implication and uses a technically difficult new argument based on a variation of Steel forcing to provide new separations.
Theorem 3.18 [Reference Goh8]
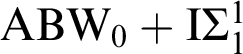 $\mathrm {ABW}_{0}+\mathrm {I}\Sigma _{1}^{1}$
is strictly stronger than finite-
$\mathrm {ABW}_{0}+\mathrm {I}\Sigma _{1}^{1}$
is strictly stronger than finite-
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
.
$\mathrm {AC}_{0}$
.
Theorem 3.19 [Reference Goh8]
![]() $\Delta _{1}^{1}$
-
$\Delta _{1}^{1}$
-
![]() $\mathrm {CA}_{0}\nvdash $
finite-
$\mathrm {CA}_{0}\nvdash $
finite-
![]() $\Sigma _{1}^{1}$
-
$\Sigma _{1}^{1}$
-
![]() $\mathrm {AC}_{0}$
and so, as
$\mathrm {AC}_{0}$
and so, as
![]() $\Delta _{1}^{1}$
-
$\Delta _{1}^{1}$
-
![]() $\mathrm {CA}_{0}\vdash $
weak-
$\mathrm {CA}_{0}\vdash $
weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
[Reference Simpson26, Example VIII.4.14], finite-
$_{0}$
[Reference Simpson26, Example VIII.4.14], finite-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
is strictly stronger than weak-
$_{0}$
is strictly stronger than weak-
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
.
$_{0}$
.
4 Almost theorems of hyperarithmetic analysis
Bowler, Carmesin, and Pott [Reference Bowler, Carmesin and Pott2, top of p. 2] sketch a reduction of
![]() $\mathrm {IRT}_{\mathrm {UES}}$
to
$\mathrm {IRT}_{\mathrm {UES}}$
to
![]() $\mathrm {IRT}_{\mathrm {UVS}}$
. While the proof sketch appears to be elementary, a closer look shows that underneath it seems to use principles that are THAs and about as strong as the ones being proven equivalent. Our expectation was that these principles, like the IRT
$\mathrm {IRT}_{\mathrm {UVS}}$
. While the proof sketch appears to be elementary, a closer look shows that underneath it seems to use principles that are THAs and about as strong as the ones being proven equivalent. Our expectation was that these principles, like the IRT
![]() $_{\mathrm {XYS}}$
, themselves would also prove to be THAs. That turned out not to be the case. Rather, the graph-theoretic principle that they used (about being able to restrict attention to locally finite graphs) implied (over ACA
$_{\mathrm {XYS}}$
, themselves would also prove to be THAs. That turned out not to be the case. Rather, the graph-theoretic principle that they used (about being able to restrict attention to locally finite graphs) implied (over ACA
![]() $_{0})$
some known THA. The unusual aspect of the situation was that we could prove that it was not possible to show that they implied any known THA in RCA
$_{0})$
some known THA. The unusual aspect of the situation was that we could prove that it was not possible to show that they implied any known THA in RCA
![]() $_{0}$
. In particular they did not even imply ACA
$_{0}$
. In particular they did not even imply ACA
![]() $_{0}$
. This led to the definition and analysis of ATHAs in [Reference Shore25] on which we report in this section. For various reasons we do not consider double rays in this section and so use only the subscripts X and Y when appropriate. For these cases, our variants of the principle they use (with UV for XY) are as follows:
$_{0}$
. This led to the definition and analysis of ATHAs in [Reference Shore25] on which we report in this section. For various reasons we do not consider double rays in this section and so use only the subscripts X and Y when appropriate. For these cases, our variants of the principle they use (with UV for XY) are as follows:
Definition 4.1.
![]() $\mathrm {LF}_{\mathrm {XY}}$
: Every X-graph which contains arbitrarily many Y-disjoint rays contains a locally finite subgraph which also contains arbitrarily many Y-disjoint rays.
$\mathrm {LF}_{\mathrm {XY}}$
: Every X-graph which contains arbitrarily many Y-disjoint rays contains a locally finite subgraph which also contains arbitrarily many Y-disjoint rays.
The starting point of our analysis is that, for each choice of X and Y, LF
![]() $_{\mathrm {XY}}$
+ ACA
$_{\mathrm {XY}}$
+ ACA
![]() $_{0}$
is equivalent to IRT
$_{0}$
is equivalent to IRT
![]() $_{\mathrm {XY}}$
over RCA
$_{\mathrm {XY}}$
over RCA
![]() $_{0}$
and so is a THA. To see that the LF
$_{0}$
and so is a THA. To see that the LF
![]() $_{\mathrm {XY}}$
are all ATHAs we need to prove that none imply ACA
$_{\mathrm {XY}}$
are all ATHAs we need to prove that none imply ACA
![]() $_{0}$
. We actually prove much more.
$_{0}$
. We actually prove much more.
We also prove by the same methods that many other principles are ATHAs. Indeed, we prove not only that they do not imply ACA
![]() $_{0}$
but that they are very weak over RCA
$_{0}$
but that they are very weak over RCA
![]() $_{0}$
. To be specific, we show that they can each be forced by a notion of forcing from a general class of tree forcings without adding branches to trees lacking them or any (of countably many specified) new sets. Moreover, any such principle is highly conservative over RCA
$_{0}$
. To be specific, we show that they can each be forced by a notion of forcing from a general class of tree forcings without adding branches to trees lacking them or any (of countably many specified) new sets. Moreover, any such principle is highly conservative over RCA
![]() $_{0}$
.
$_{0}$
.
Definition 4.2. Each of our classes of formulas consists of a base class which includes the quantifier-free formulas and is then closed under conjunction (
![]() $\wedge $
), disjunction (
$\wedge $
), disjunction (
![]() $\vee $
), first-order quantification (
$\vee $
), first-order quantification (
![]() $\forall x$
and
$\forall x$
and
![]() $\exists x$
for number variables), and universal second-order quantification (
$\exists x$
for number variables), and universal second-order quantification (
![]() $\forall X$
for set variables). The G-
$\forall X$
for set variables). The G-
 $\Pi _{1}^{1}$
class of formulas has only the quantifier free ones in its base. The G-r-
$\Pi _{1}^{1}$
class of formulas has only the quantifier free ones in its base. The G-r-
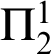 $\Pi _{2}^{1}$
class of formulas also has in its base all formulas which are of the form
$\Pi _{2}^{1}$
class of formulas also has in its base all formulas which are of the form
![]() $\exists Y\Theta (Y)$
where
$\exists Y\Theta (Y)$
where
![]() $\Theta $
is
$\Theta $
is
![]() $\Sigma _{3}^{0}$
. The G-Tanaka class of formulas instead adds to the base class all formulas of the form
$\Sigma _{3}^{0}$
. The G-Tanaka class of formulas instead adds to the base class all formulas of the form
![]() $\exists !\!Y\Phi (Y)$
for arithmetic
$\exists !\!Y\Phi (Y)$
for arithmetic
![]() $\Phi $
. The G-r-Tanaka class also includes in its base all formulas of the form
$\Phi $
. The G-r-Tanaka class also includes in its base all formulas of the form
![]() $\exists !\!Y\exists Z\Psi (\bar {x},Y,Z)$
with
$\exists !\!Y\exists Z\Psi (\bar {x},Y,Z)$
with
![]() $\Psi $
a
$\Psi $
a
![]() $\Sigma _{3}^{0}$
formula. For a class
$\Sigma _{3}^{0}$
formula. For a class
![]() $\Gamma $
of formulas, a theory T is
$\Gamma $
of formulas, a theory T is
![]() $\Gamma $
-conservative over one S if, for every sentence
$\Gamma $
-conservative over one S if, for every sentence
![]() $\varphi \in \Gamma $
,
$\varphi \in \Gamma $
,
![]() $T\vdash \varphi \rightarrow S\vdash \varphi $
. If S is RCA
$T\vdash \varphi \rightarrow S\vdash \varphi $
. If S is RCA
![]() $_{0}$
we omit mentioning it.
$_{0}$
we omit mentioning it.
We assume a basic familiarity with forcing. This can be carried over to forcing over models of second-order arithmetic satisfying RCA
![]() $_{0}$
without too much trouble. Our basic class of tree forcings have many familiar examples even with the effectiveness notion we require. The definition of the uniform version is more technical but most of the familiar examples are also uniform or can be made so.
$_{0}$
without too much trouble. Our basic class of tree forcings have many familiar examples even with the effectiveness notion we require. The definition of the uniform version is more technical but most of the familiar examples are also uniform or can be made so.
Definition 4.3. A notion of forcing
![]() $\mathcal {P}=\left \langle P,\leq \right \rangle $
is a tree forcing
$\mathcal {P}=\left \langle P,\leq \right \rangle $
is a tree forcing
![]() $($
t-forcing
$($
t-forcing
![]() $)$
if the following hold:
$)$
if the following hold:
-
1. Conditions in
 $\mathcal {P}$
are of the form
$\mathcal {P}$
are of the form
 $\left \langle \tau ,T\right \rangle $
where
$\left \langle \tau ,T\right \rangle $
where
 $T\in S(N)$
is a subtree of
$T\in S(N)$
is a subtree of
 $N^{<N}$
(i.e., a subset of
$N^{<N}$
(i.e., a subset of
 $N^{<N}$
in
$N^{<N}$
in
 $\mathcal {N}$
closed under initial segments with respect to
$\mathcal {N}$
closed under initial segments with respect to
 $\subseteq $
) and
$\subseteq $
) and
 $\tau $
is comparable with every
$\tau $
is comparable with every
 $\sigma \in T$
. The root of T is taken to be the empty string. The stem of T is defined to be the longest string comparable with every element of T.
$\sigma \in T$
. The root of T is taken to be the empty string. The stem of T is defined to be the longest string comparable with every element of T. -
2. If
 $\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
then
$\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
then
 $\tau ^{\prime }\supseteq \tau $
and
$\tau ^{\prime }\supseteq \tau $
and
 $T^{\prime }\subseteq T$
.
$T^{\prime }\subseteq T$
. -
3. For every
 $n\in N$
the class
$n\in N$
the class
 $\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
is dense in
$\{\left \langle \tau ,T\right \rangle ||\tau |\geq n\}$
is dense in
 $\mathcal {P}$
, i.e.,
$\mathcal {P}$
, i.e.,
 ${(\forall \left \langle \tau ,T\right \rangle \in \mathcal {P})} (\exists \left \langle \tau ^{\prime },T^{\prime }\right \rangle )(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle ~\&~|\tau ^{\prime }|\geq n)$
.
${(\forall \left \langle \tau ,T\right \rangle \in \mathcal {P})} (\exists \left \langle \tau ^{\prime },T^{\prime }\right \rangle )(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle ~\&~|\tau ^{\prime }|\geq n)$
.
Definition 4.4. A tree notion of forcing
![]() $\mathcal {P}$
is an effective tree forcing (et-forcing) if, for every
$\mathcal {P}$
is an effective tree forcing (et-forcing) if, for every
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {P}$
, the class
$\left \langle \tau ,T\right \rangle \in \mathcal {P}$
, the class
![]() $Ext(\left \langle \tau ,T\right \rangle )=\{\tau ^{\prime }|(\exists T^{\prime })(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle )\}$
is
$Ext(\left \langle \tau ,T\right \rangle )=\{\tau ^{\prime }|(\exists T^{\prime })(\left \langle \tau ^{\prime },T^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle )\}$
is
![]() $\boldsymbol {\Sigma }_{1}^{0}$
, i.e., there is an
$\boldsymbol {\Sigma }_{1}^{0}$
, i.e., there is an
![]() $A\in S(\mathcal{N})$
such that
$A\in S(\mathcal{N})$
such that
![]() $Ext(\left \langle \tau ,T\right \rangle )$
is
$Ext(\left \langle \tau ,T\right \rangle )$
is
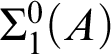 $\Sigma _{1}^{0}(A)$
(over N).
$\Sigma _{1}^{0}(A)$
(over N).
Definition 4.5. An et-forcing
![]() $\mathcal {P}$
is uniform
$\mathcal {P}$
is uniform
![]() $($
a uet-forcing
$($
a uet-forcing
![]() $)$
if, for every condition
$)$
if, for every condition
![]() $\left \langle \tau ,T\right \rangle $
, every
$\left \langle \tau ,T\right \rangle $
, every
![]() $\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
with
$\rho ,\sigma \in Ext(\left \langle \tau ,T\right \rangle )$
with
![]() $|\rho |=|\sigma |$
, and every
$|\rho |=|\sigma |$
, and every
![]() $\left \langle \rho ^{\prime \prime },R^{\prime \prime }\right \rangle \leq \left \langle \rho ^{\prime },R^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with
$\left \langle \rho ^{\prime \prime },R^{\prime \prime }\right \rangle \leq \left \langle \rho ^{\prime },R^{\prime }\right \rangle \leq \left \langle \tau ,T\right \rangle $
with
![]() $\rho \subseteq \rho ^{\prime } $
,
$\rho \subseteq \rho ^{\prime } $
,
![]() $\left \langle \rho _{\sigma }^{\prime \prime },R_{\sigma }^{\prime \prime }\right \rangle \leq \left \langle \rho _{\sigma }^{\prime },R^{\prime }_{\sigma }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. For technical convenience we also require that if
$\left \langle \rho _{\sigma }^{\prime \prime },R_{\sigma }^{\prime \prime }\right \rangle \leq \left \langle \rho _{\sigma }^{\prime },R^{\prime }_{\sigma }\right \rangle \leq \left \langle \tau ,T\right \rangle $
. For technical convenience we also require that if
![]() $\left \langle \tau ,T\right \rangle \in \mathcal {P}$
and the stem of T is some
$\left \langle \tau ,T\right \rangle \in \mathcal {P}$
and the stem of T is some
![]() $\sigma \supset \tau $
then
$\sigma \supset \tau $
then
![]() $\left \langle \rho ,T\right \rangle \leq \left \langle \tau ,T\right \rangle $
whenever
$\left \langle \rho ,T\right \rangle \leq \left \langle \tau ,T\right \rangle $
whenever
![]() $\sigma \supseteq \rho \supseteq \tau $
. Note: For
$\sigma \supseteq \rho \supseteq \tau $
. Note: For
![]() $\sigma \in T$
,
$\sigma \in T$
,
![]() $T_{\sigma }=\{\mu _{\sigma }|\mu \in T\}$
where
$T_{\sigma }=\{\mu _{\sigma }|\mu \in T\}$
where
![]() $\mu _{\sigma }(i)=\sigma (i)$
for
$\mu _{\sigma }(i)=\sigma (i)$
for
![]() $i<|\sigma |$
and
$i<|\sigma |$
and
![]() $\mu _{\sigma }(i)=\mu (i)$
for
$\mu _{\sigma }(i)=\mu (i)$
for
![]() $i\geq |\sigma |$
.
$i\geq |\sigma |$
.
Common examples of uet-forcings are Cohen, Mathias, and Silver forcings and many variations. The usual versions of Laver and Sacks forcings are et but not uniform. Sacks forcing can be made so by using “uniform” trees as in [Reference Lerman16, Definition VI.2.3]. A similar variation can be applied to Laver forcing. We now want to know that these notions of forcing have various preservation properties.
Theorem 4.6. If
![]() $\mathcal {P}$
is an et-forcing over a countable model
$\mathcal {P}$
is an et-forcing over a countable model
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathrm {RCA}_{0}$
, there is a countable collection
$\mathrm {RCA}_{0}$
, there is a countable collection
![]() $\mathcal {D}$
of dense sets (including the ones specified in Definition 4.3) such that
$\mathcal {D}$
of dense sets (including the ones specified in Definition 4.3) such that
-
1. If G is
 $\mathcal {P}$
-generic for
$\mathcal {P}$
-generic for
 $\mathcal {D}$
, then
$\mathcal {D}$
, then
 $\mathcal {N} [G]\vDash \mathrm {RCA}_{0}$
.
$\mathcal {N} [G]\vDash \mathrm {RCA}_{0}$
. -
2. If R is a subtree of
 $N^{<N} \ ($
not necessarily in
$N^{<N} \ ($
not necessarily in
 $S(\mathcal {N)})$
with no branch in
$S(\mathcal {N)})$
with no branch in
 $S(\mathcal {N})$
, then there is a countable collection
$S(\mathcal {N})$
, then there is a countable collection
 $\mathcal {D}^{\prime }\supseteq \mathcal {D}$
of dense sets such that if G is
$\mathcal {D}^{\prime }\supseteq \mathcal {D}$
of dense sets such that if G is
 $\mathcal {P}$
-generic for
$\mathcal {P}$
-generic for
 $\mathcal {D}^{\prime }$
, then there is no branch of R in
$\mathcal {D}^{\prime }$
, then there is no branch of R in
 $\mathcal {N}[G]$
.
$\mathcal {N}[G]$
. -
3. Thus for any countable collection
 $R_{i}$
of trees as in 2
$R_{i}$
of trees as in 2
 $($
such as all those in
$($
such as all those in
 $S(\mathcal {N)})$
there is a single
$S(\mathcal {N)})$
there is a single
 $\mathcal {D}^{\prime }$
as in 2 which works for every
$\mathcal {D}^{\prime }$
as in 2 which works for every
 $R_{i}$
. In particular, for a set
$R_{i}$
. In particular, for a set
 $\{C_{i}|i\in \omega \}$
with
$\{C_{i}|i\in \omega \}$
with
 $C_{i}\subseteq N$
and
$C_{i}\subseteq N$
and
 $C_{i}\notin S(\mathcal {N)}$
for every
$C_{i}\notin S(\mathcal {N)}$
for every
 $i\in \omega $
, there is a
$i\in \omega $
, there is a
 $\mathcal {D}^{\prime }\supseteq \mathcal {D}$
such that, for any
$\mathcal {D}^{\prime }\supseteq \mathcal {D}$
such that, for any
 $\mathcal {D}^{\prime }$
-generic G, no
$\mathcal {D}^{\prime }$
-generic G, no
 $C_{i}\in \mathcal {N}[G]$
.
$C_{i}\in \mathcal {N}[G]$
.
It is now easy to see that if, for any theory T and countable model
![]() $\mathcal {N}$
of RCA
$\mathcal {N}$
of RCA
![]() $_{0}$
, we can iterate et-forcings to produce an extension
$_{0}$
, we can iterate et-forcings to produce an extension
![]() $\mathcal {N}_{\infty }\vDash T$
,
$\mathcal {N}_{\infty }\vDash T$
,
![]() $T\nvdash \mathrm {ACA}_{0}$
. (Start with the recursive sets as
$T\nvdash \mathrm {ACA}_{0}$
. (Start with the recursive sets as
![]() $\mathcal {N}$
and iterate the forcings without adding the set
$\mathcal {N}$
and iterate the forcings without adding the set
![]() $0^{\prime }$
.) So no such T can be a THA.
$0^{\prime }$
.) So no such T can be a THA.
We want to prove that we can also use these notions of forcing to derive the
![]() $\Gamma $
-conservativity of theories T for the classes
$\Gamma $
-conservativity of theories T for the classes
![]() $\Gamma $
of Definition 4.2. All of our proofs have the same general format. For the sake of a contradiction, we assume that there is a sentence
$\Gamma $
of Definition 4.2. All of our proofs have the same general format. For the sake of a contradiction, we assume that there is a sentence
![]() $\Lambda \in \Gamma $
such that
$\Lambda \in \Gamma $
such that
![]() $T\vdash \Lambda $
and a countable model
$T\vdash \Lambda $
and a countable model
![]() $\mathcal {N}\vDash \lnot \Lambda $
of RCA
$\mathcal {N}\vDash \lnot \Lambda $
of RCA
![]() $_{0}$
. We then construct, by iterated forcing, a model
$_{0}$
. We then construct, by iterated forcing, a model
![]() $\mathcal {N} _{\infty }$
of T. If we can also guarantee that
$\mathcal {N} _{\infty }$
of T. If we can also guarantee that
![]() $\mathcal {N}_{\infty } \vDash \lnot \Lambda $
, we have proven
$\mathcal {N}_{\infty } \vDash \lnot \Lambda $
, we have proven
![]() $\Gamma $
-conservativity.
$\Gamma $
-conservativity.
Typical arguments of this sort deal with T whose axioms (other than RCA
![]() $_{0}$
) are
$_{0}$
) are
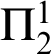 $\Pi _{2}^{1}$
principles, i.e., sentences of the form
$\Pi _{2}^{1}$
principles, i.e., sentences of the form
![]() $\forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y))$
with
$\forall X(\Phi (X)\rightarrow \exists Y\Psi (X,Y))$
with
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
arithmetic. One shows that for each such axiom Q and countable model
$\Psi $
arithmetic. One shows that for each such axiom Q and countable model
![]() $\mathcal {M}$
of RCA
$\mathcal {M}$
of RCA
![]() $_{0}$
and instance of Q given by some X with
$_{0}$
and instance of Q given by some X with
![]() $\mathcal {M}\vDash \Phi (X)$
, one has a notion of forcing and a collection of dense sets such that, for any generic G,
$\mathcal {M}\vDash \Phi (X)$
, one has a notion of forcing and a collection of dense sets such that, for any generic G,
![]() $\mathcal {M}[G]\vDash \exists Y\Psi (X,Y)$
. (We say that the forcing adds a solution for the instance of Q given by X.) One can then perform an
$\mathcal {M}[G]\vDash \exists Y\Psi (X,Y)$
. (We say that the forcing adds a solution for the instance of Q given by X.) One can then perform an
![]() $\omega $
length iteration to construct
$\omega $
length iteration to construct
![]() $\mathcal {M} _{\infty }$
such that each instance of each
$\mathcal {M} _{\infty }$
such that each instance of each
![]() $Q\in Y$
in
$Q\in Y$
in
![]() $\mathcal {M}_{\infty }$
gets a witness there as well. As
$\mathcal {M}_{\infty }$
gets a witness there as well. As
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}_{\infty }$
have the same first-order part, it is easy to see that
$\mathcal {M}_{\infty }$
have the same first-order part, it is easy to see that
![]() $\mathcal {M}_{\infty }\vDash T$
and any
$\mathcal {M}_{\infty }\vDash T$
and any
 $\Pi _{1}^{1}$
sentence
$\Pi _{1}^{1}$
sentence
![]() $\Lambda $
false in
$\Lambda $
false in
![]() $\mathcal {M}$
remains false in
$\mathcal {M}$
remains false in
![]() $\mathcal {M}_{\infty }$
. The crucial point here is that as
$\mathcal {M}_{\infty }$
. The crucial point here is that as
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are arithmetic, truth and falsity of all instances of Q are preserved upward in the iteration. We prove that the truth of negations of G-
$\Psi $
are arithmetic, truth and falsity of all instances of Q are preserved upward in the iteration. We prove that the truth of negations of G-
 $\Pi _{1}^{1}$
sentences are also preserved by an induction argument. If the forcings needed are et then we get G-r-
$\Pi _{1}^{1}$
sentences are also preserved by an induction argument. If the forcings needed are et then we get G-r-
 $\Pi _{2}^{1}$
conservativity. If the forcings are uet, we get G-Tanaka and G-r-Tanaka conservativity. These results strengthen many known conservation theorems.
$\Pi _{2}^{1}$
conservativity. If the forcings are uet, we get G-Tanaka and G-r-Tanaka conservativity. These results strengthen many known conservation theorems.
In terms of ATHAs and various stronger principles, however, we are interested in situations where the axioms of T are more complicated. Our starting examples are the LF
![]() $_{\mathrm {XY}}$
(Definition 4.1). Here the axioms/principles Q are as above but
$_{\mathrm {XY}}$
(Definition 4.1). Here the axioms/principles Q are as above but
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are of the form
$\Psi $
are of the form
![]() $\forall n\exists Z\Theta $
with
$\forall n\exists Z\Theta $
with
![]() $\Theta $
arithmetic (saying Z is a sequence of disjoint rays of length n). We prove that for any graph which is an instance of an LF
$\Theta $
arithmetic (saying Z is a sequence of disjoint rays of length n). We prove that for any graph which is an instance of an LF
![]() $_{\mathrm {XY}}$
there is an et (indeed uet) forcing that adds a solution, i.e., a locally finite subgraph with the desired sequences of disjoint rays. While the added solutions remain solutions in
$_{\mathrm {XY}}$
there is an et (indeed uet) forcing that adds a solution, i.e., a locally finite subgraph with the desired sequences of disjoint rays. While the added solutions remain solutions in
![]() $\mathcal {N} _{\infty }$
, we may have new instances that did not seem to be instances at any point along the way: The required witnesses Z for some X may appear cofinally in the iteration. So
$\mathcal {N} _{\infty }$
, we may have new instances that did not seem to be instances at any point along the way: The required witnesses Z for some X may appear cofinally in the iteration. So
![]() $\mathcal {N}_{\infty }$
may not be a model of LF
$\mathcal {N}_{\infty }$
may not be a model of LF
![]() $_{\mathrm {XY}} $
. The natural plan here is to continue the iteration to length
$_{\mathrm {XY}} $
. The natural plan here is to continue the iteration to length
![]() $\omega _{1}$
as any assumed witnesses for an X appearing in
$\omega _{1}$
as any assumed witnesses for an X appearing in
![]() $\mathcal {N}_{\infty } $
must then also all appear at some stage of the length
$\mathcal {N}_{\infty } $
must then also all appear at some stage of the length
![]() $\omega _{1}$
iteration and so have a solution added at some point as well.
$\omega _{1}$
iteration and so have a solution added at some point as well.
Theorem 4.7. For each of the
![]() $\mathrm {LF}_{\mathrm {XY}}$
there are uet-forcings that add solutions for any instance. Thus all of them together are G-r-Tanaka (and so G-Tanaka, G-r-
$\mathrm {LF}_{\mathrm {XY}}$
there are uet-forcings that add solutions for any instance. Thus all of them together are G-r-Tanaka (and so G-Tanaka, G-r-
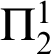 $\Pi _{2}^{1}$
, and G-
$\Pi _{2}^{1}$
, and G-
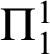 $\Pi _{1}^{1}$
) conservative over
$\Pi _{1}^{1}$
) conservative over
![]() $\mathrm {RCA}_{0}$
. As over
$\mathrm {RCA}_{0}$
. As over
![]() $\mathrm {ACA}_{0}$
each implies
$\mathrm {ACA}_{0}$
each implies
![]() $\mathrm {IRT}_{\mathrm {XY}}$
which is a THA, each of them is an ATHA.
$\mathrm {IRT}_{\mathrm {XY}}$
which is a THA, each of them is an ATHA.
The SCR
![]() $_{XY}$
are equivalents of the corresponding IRT
$_{XY}$
are equivalents of the corresponding IRT
![]() $_{\mathrm {XY}}$
. We can adjust them slightly to get other ATHAs which are equivalent to IRT
$_{\mathrm {XY}}$
. We can adjust them slightly to get other ATHAs which are equivalent to IRT
![]() $_{ \mathrm {XY}}$
only over ACA
$_{ \mathrm {XY}}$
only over ACA
![]() $_{0}$
. One example is that we just require that the sequence
$_{0}$
. One example is that we just require that the sequence
![]() $\langle R^{n}\rangle $
has each
$\langle R^{n}\rangle $
has each
![]() $R^{n}$
being a sequence of almost (i.e., up to finite difference) disjoint rays of length n. We also consider variations of an array of known strong principles that provide versions that are
$R^{n}$
being a sequence of almost (i.e., up to finite difference) disjoint rays of length n. We also consider variations of an array of known strong principles that provide versions that are
![]() $\Gamma $
-conservative for all the class of Definition 4.2 but very strong over ACA
$\Gamma $
-conservative for all the class of Definition 4.2 but very strong over ACA
![]() $_{0}$
.
$_{0}$
.
Definition 4.8.
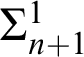 $\Sigma _{n+1}^{1}$
-AC
$\Sigma _{n+1}^{1}$
-AC
![]() $^{\ast }$
:
$^{\ast }$
:
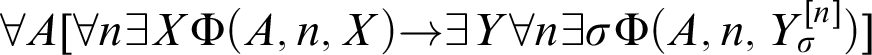 $\forall A[\forall n\exists X\Phi (A,n,X){\rightarrow} \exists Y\forall n\exists \sigma \Phi (A,n, Y_{\sigma }^{[n]})]$
, for
$\forall A[\forall n\exists X\Phi (A,n,X){\rightarrow} \exists Y\forall n\exists \sigma \Phi (A,n, Y_{\sigma }^{[n]})]$
, for
 $\Phi \ \Pi _{n}^{1}$
.
$\Phi \ \Pi _{n}^{1}$
.
(Note: For
![]() $Y \in N^N$
and
$Y \in N^N$
and
![]() $\sigma \in N^{<N}$
, we define
$\sigma \in N^{<N}$
, we define
![]() $Y_\sigma $
by
$Y_\sigma $
by
![]() $Y_\sigma (i) = \sigma (i)$
for
$Y_\sigma (i) = \sigma (i)$
for
![]() $i < |\sigma |$
and
$i < |\sigma |$
and
![]() $Y_\sigma (i) = Y(i)$
for
$Y_\sigma (i) = Y(i)$
for
![]() $i \geq |\sigma |$
.)
$i \geq |\sigma |$
.)
 $\Sigma _{n+1}^{1}$
-AC
$\Sigma _{n+1}^{1}$
-AC
![]() $^{-}$
:
$^{-}$
:
![]() $\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists m\Phi (A,n,Y^{[m]})]$
for
$\forall A[\forall n\exists X\Phi (A,n,X)\rightarrow \exists Y\forall n\exists m\Phi (A,n,Y^{[m]})]$
for
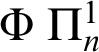 $\Phi \ \Pi _{n}^{1}$
.
$\Phi \ \Pi _{n}^{1}$
.
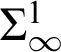 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
and
$^{\ast }$
and
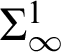 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}$
assert, respectively, that
$^{-}$
assert, respectively, that
![]() $\Sigma _{n}^{1}$
-AC
$\Sigma _{n}^{1}$
-AC
![]() $^{\ast }$
and
$^{\ast }$
and
![]() $\Sigma _{n}^{1}$
-AC
$\Sigma _{n}^{1}$
-AC
![]() $^{-}$
hold for all
$^{-}$
hold for all
![]() $n\in \omega $
.
$n\in \omega $
.
Theorem 4.9. For each
![]() $n\in \omega $
,
$n\in \omega $
,
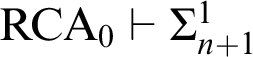 $\mathrm {RCA}_{0}\vdash \Sigma _{n+1}^{1}$
-
$\mathrm {RCA}_{0}\vdash \Sigma _{n+1}^{1}$
-
 $\mathrm {AC}\rightarrow \Sigma _{n+1}^{1}$
-
$\mathrm {AC}\rightarrow \Sigma _{n+1}^{1}$
-
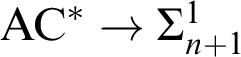 $\mathrm {AC}^{\ast }\rightarrow \Sigma _{n+1}^{1}$
-
$\mathrm {AC}^{\ast }\rightarrow \Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}^{-}$
and
$\mathrm {AC}^{-}$
and
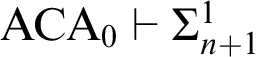 $\mathrm {ACA}_{0}\vdash \Sigma _{n+1}^{1}$
-
$\mathrm {ACA}_{0}\vdash \Sigma _{n+1}^{1}$
-
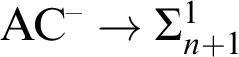 $\mathrm {AC}^{-}\rightarrow \Sigma _{n+1}^{1}$
-
$\mathrm {AC}^{-}\rightarrow \Sigma _{n+1}^{1}$
-
![]() $\mathrm {CA}$
. So over
$\mathrm {CA}$
. So over
![]() $\mathrm {ACA}_{0}$
, all of
$\mathrm {ACA}_{0}$
, all of
 $\Sigma _{\infty }^{1}$
-
$\Sigma _{\infty }^{1}$
-
![]() $\mathrm {AC}^{\ast }$
,
$\mathrm {AC}^{\ast }$
,
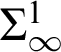 $\Sigma _{\infty }^{1}$
-
$\Sigma _{\infty }^{1}$
-
![]() $\mathrm {AC}^{-}$
, and
$\mathrm {AC}^{-}$
, and
 $\Sigma _{\infty }^{1}$
-
$\Sigma _{\infty }^{1}$
-
![]() $\mathrm {CA}$
are equivalent as are
$\mathrm {CA}$
are equivalent as are
 $\Sigma _{n+1}^{1}$
-
$\Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}$
,
$\mathrm {AC}$
,
 $\Sigma _{n+1}^{1}$
-
$\Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}^{\ast }$
, and
$\mathrm {AC}^{\ast }$
, and
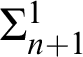 $\Sigma _{n+1}^{1}$
-
$\Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}^{-}$
for each n.
$\mathrm {AC}^{-}$
for each n.
Theorem 4.10.
 $\Sigma _{\infty }^{1}$
-
$\Sigma _{\infty }^{1}$
-
![]() $\mathrm {AC}_{0}^{\ast }$
is
$\mathrm {AC}_{0}^{\ast }$
is
![]() $\Gamma $
-conservative for all the classes
$\Gamma $
-conservative for all the classes
![]() $\Gamma $
of Definition 4.2 and so are all the
$\Gamma $
of Definition 4.2 and so are all the
 $\Sigma _{n+1}^{1}$
-
$\Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}^{\ast }_{0}$
and
$\mathrm {AC}^{\ast }_{0}$
and
 $\Sigma _{n+1}^{1}$
-
$\Sigma _{n+1}^{1}$
-
![]() $\mathrm {AC}^{-}_{0}$
by the previous theorem.
$\mathrm {AC}^{-}_{0}$
by the previous theorem.
So, in particular,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}^{\ast }$
,
$_{0}^{\ast }$
,
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}^{-}$
,
$_{0}^{-}$
,
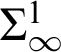 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $_{0}^{\ast }$
, and
$_{0}^{\ast }$
, and
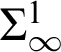 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{-}_{0}$
are highly conservative over RCA
$^{-}_{0}$
are highly conservative over RCA
![]() $_{0}$
but over ACA
$_{0}$
but over ACA
![]() $_{0}$
each of the first pair is equivalent to
$_{0}$
each of the first pair is equivalent to
![]() $\Sigma _{1}^{1}$
-AC
$\Sigma _{1}^{1}$
-AC
![]() $_{0}$
(and so are ATHAs) and each of the second pair is equivalent to
$_{0}$
(and so are ATHAs) and each of the second pair is equivalent to
 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $_{0}$
and so stronger than full second-order arithmetic. (See [Reference Simpson26, Remark VII.6.3].) Some earlier conservation results for some of the theories covered here are in [Reference Kihara14, Reference Yamazaki30 and Reference Yokoyama32] as well as in work by Tanaka, Montalbán and Yamazaki as reported in [Reference Yamazaki31].
$_{0}$
and so stronger than full second-order arithmetic. (See [Reference Simpson26, Remark VII.6.3].) Some earlier conservation results for some of the theories covered here are in [Reference Kihara14, Reference Yamazaki30 and Reference Yokoyama32] as well as in work by Tanaka, Montalbán and Yamazaki as reported in [Reference Yamazaki31].
The proof of Theorem 4.9 is combinatorial and proceeds by induction on n. Theorem 4.10 is proven by providing et- or even uet-forcings that add solutions for
 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
. Now
$^{\ast }$
. Now
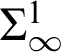 $\Sigma _{\infty }^{1}$
-AC
$\Sigma _{\infty }^{1}$
-AC
![]() $^{\ast }$
has both hypotheses/instances
$^{\ast }$
has both hypotheses/instances
![]() $\Phi (X)$
and conclusions/solutions
$\Phi (X)$
and conclusions/solutions
![]() $\Psi (X,Y)$
of arbitrary complexity. Thus we need another idea to guarantee that adding what looks like a solution stays a solution in
$\Psi (X,Y)$
of arbitrary complexity. Thus we need another idea to guarantee that adding what looks like a solution stays a solution in
![]() $\mathcal {N}_{\infty }$
as well as a procedure that makes sure we handle everything that is an instance in
$\mathcal {N}_{\infty }$
as well as a procedure that makes sure we handle everything that is an instance in
![]() $\mathcal {N}_{\infty }$
along the way. The crucial idea here is to use the fact that if we do an
$\mathcal {N}_{\infty }$
along the way. The crucial idea here is to use the fact that if we do an
![]() $\omega _{1}$
iteration to produce models
$\omega _{1}$
iteration to produce models
![]() $\mathcal {N}_{\alpha }$
for
$\mathcal {N}_{\alpha }$
for
![]() $\alpha <\omega _{1}$
then, for a closed unbounded set of
$\alpha <\omega _{1}$
then, for a closed unbounded set of
![]() $\lambda <\omega _{1}$
,
$\lambda <\omega _{1}$
,
![]() $\mathcal {N}_{\lambda }$
will be an elementary submodel of
$\mathcal {N}_{\lambda }$
will be an elementary submodel of
![]() $\mathcal {N} _{\infty }$
. Thus, if we carefully handle everything that looks like an instance in such an
$\mathcal {N} _{\infty }$
. Thus, if we carefully handle everything that looks like an instance in such an
![]() $\mathcal {N}_{\lambda }$
and supply something that looks like a solution, all will be well at the end.
$\mathcal {N}_{\lambda }$
and supply something that looks like a solution, all will be well at the end.
We view these results and the previous ones on ATHAs that are equivalent to known THAs over ACA
![]() $_{0}$
as supplying answers to the question raised by Hirschfeldt and repeated in [Reference Montalbán19] by providing an ample list of many pairs of principles that are very different over RCA
$_{0}$
as supplying answers to the question raised by Hirschfeldt and repeated in [Reference Montalbán19] by providing an ample list of many pairs of principles that are very different over RCA
![]() $_{0}$
but equivalent over ACA
$_{0}$
but equivalent over ACA
![]() $_{0}$
. It could well be argued that these weak ones should really be seen as the same as their strong counterparts in an analysis that works over ACA
$_{0}$
. It could well be argued that these weak ones should really be seen as the same as their strong counterparts in an analysis that works over ACA
![]() $_{0}$
rather than RCA
$_{0}$
rather than RCA
![]() $_{0}$
.
$_{0}$
.
Acknowledgment
All the authors were partially supported by NSF Grant DMS-1161175.