Article contents
The Stable core
Published online by Cambridge University Press: 15 January 2014
Abstract
Vopěnka proved long ago that every set of ordinals is set-generic over HOD, Gödel's inner model of hereditarily ordinal-definable sets. Here we show that the entire universe V is class-generic over (HOD,S), and indeed over the even smaller inner model 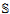 =(L[S],S), where S is the Stability predicate. We refer to the inner model
=(L[S],S), where S is the Stability predicate. We refer to the inner model 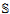 as the Stable Core of V. The predicate S has a simple definition which is more absolute than any definition of HOD; in particular, it is possible to add reals which are not set-generic but preserve the Stable Core (this is not possible for HOD by Vopěnka's theorem).
as the Stable Core of V. The predicate S has a simple definition which is more absolute than any definition of HOD; in particular, it is possible to add reals which are not set-generic but preserve the Stable Core (this is not possible for HOD by Vopěnka's theorem).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 3
- Cited by


