Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T06:08:50.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Recent Advances in Ordinal Analysis: Π12 — CA and Related Systems

Published online by Cambridge University Press:  15 January 2014

Michael Rathjen
Michael Rathjen*
Affiliation:
Department of Mathematics, Stanford University Stanford, California 94305, USA.E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

§1. Introduction. The purpose of this paper is, in general, to report the state of the art of ordinal analysis and, in particular, the recent success in obtaining an ordinal analysis for the system of 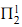-analysis, which is the subsystem of formal second order arithmetic, Z2, with comprehension confined to 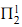-formulae. The same techniques can be used to provide ordinal analyses for theories that are reducible to iterated 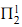-comprehension, e.g., 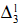-comprehension. The details will be laid out in [28].

Ordinal-theoretic proof theory came into existence in 1936, springing forth from Gentzen's head in the course of his consistency proof of arithmetic. Gentzen fostered hopes that with sufficiently large constructive ordinals one could establish the consistency of analysis, i.e., Z2. Considerable progress has been made in proof theory since Gentzen's tragic death on August 4th, 1945, but an ordinal analysis of Z2 is still something to be sought. However, for reasons that cannot be explained here, 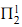-comprehension appears to be the main stumbling block on the road to understanding full comprehension, giving hope for an ordinal analysis of Z2 in the foreseeable future.

Roughly speaking, ordinally informative proof theory attaches ordinals in a recursive representation system to proofs in a given formal system; transformations on proofs to certain canonical forms are then partially mirrored by operations on the associated ordinals. Among other things, ordinal analysis of a formal system serves to characterize its provably recursive ordinals, functions and functionals and can yield both conservation and combinatorial independence results.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 1 , Issue 4 , December 1995 , pp. 468 - 485
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[2] Buchholz, W., Eine Erweiterung der Schnitteliminationsmethode, Habilitationsschrift, München, 1977.Google Scholar
[3] Buchholz, W., A simplified version of local predicativity, Leeds proof theory 1991, Cambridge University Press, Cambridge, 1993, pp. 115–147.Google Scholar
[4] Buchholz, W., Feferman, S., Pohlers, W., and Sieg, W., Iterated inductive definitions and subsystems of analysis, Springer-Verlag, Berlin, 1981.Google Scholar
[5] Buchholz, W. and Schütte, K., Proof theory of impredicative subsystems of analysis, Bibliopolis, Naples, 1988.Google Scholar
[6] Feferman, S., Systems of predicative analysis, Journal of Symbolic Logic, vol. 29 (1964), pp. 1–30.Google Scholar
[7] Feferman, S., A language and axioms for explicit mathematics, Lecture notes in mathematics 450, Springer-Verlag, Berlin, 1975, pp. 87–139.Google Scholar
[8] Feferman, S., Constructive theories of functions and classes, Logic colloquium '78, North-Holland, Amsterdam, 1979, pp. 159–224.Google Scholar
[9] Feferman, S., Proof theory: a personal report, Proof theory (Takeuti, G., editor), North-Holland, Amsterdam, second ed., 1987, pp. 445–485.Google Scholar
[10] Feferman, S., Hilbert's program relativized: Proof-theoretical and foundational reductions, Journal of Symbolic Logic, vol. 53 (1988), pp. 364–384.Google Scholar
[11] Feferman, S., Remarks for “the trends in logic”, Logic colloquium '88, North-Holland, Amsterdam, 1989, pp. 361–363.Google Scholar
[12] Friedman, H., Robertson, N., and Seymour, P., The metamathematics of the graph minor theorem, Contemporary Mathematics, vol. 65 (1987), pp. 229–261.Google Scholar
[13] Girard, J.-Y., Introduction to –logic, Synthese, vol. 62 (1985), pp. 191–216.CrossRefGoogle Scholar
[14] Gödel, K., The modern development of the foundations of mathematics in the light of philosophy, K. Gödel, Collected works, vol. III, Oxford University Press, Oxford, 1995, pp. 374–387.Google Scholar
[15] Griffor, E. and Rathjen, M., The strength of some Martin-Löf type theories, Archive for Mathematical Logic, vol. 33 (1994), pp. 347–385.CrossRefGoogle Scholar
[16] Hilbert, D., Die Grundlegung der elementaren Zahlentheorie, Mathematische Annalen, vol. 104 (1931).Google Scholar
[17] Jäger, G., Beweistheorie von KPN, Archiv für Mathematische Logik und Grundlagenforschung, vol. 20 (1980), pp. 53–64.Google Scholar
[18] Jäger, G., Zur Beweistheorie der Kripke-Platek Mengenlehre über den natürlichen Zahlen, Archiv für Mathematische Logik und Grundlagenforschung, vol. 22 (1982), pp. 121–139.Google Scholar
[19] Jäger, G., A well-ordering proof for Feferman s theory T0 , Archiv für Mathematische Logik und Grundlagenforschung, vol. 23 (1983), pp. 65–77.CrossRefGoogle Scholar
[20] Jäger, G. and Pohlers, W., Eine beweistheoretische Untersuchung von — CA + BI und verwandter Systeme, Sitzungsberichte der Bayerischen Akademie der Wissenschaften, Mathematisch–Naturwissenschaftliche Klasse, 1982.Google Scholar
[21] Jensen, R. B., The fine structure of the constructible hierarchy, Annals of Math. Logic, vol. 4 (1972), pp. 229–308.Google Scholar
[22] Martin, D. and Steel, J., Projective determinacy, Proceedings of the National Academy of Sciences ofthe United States of America, vol. 85, 1988, pp. 6582–6586.Google Scholar
[23] Martin-Löf, P., Intuitionistic type theory, Bibliopolis, Naples, 1984.Google Scholar
[24] Pohlers, W., Proof-theoretical analysis of IDv by the method of localpredicativity, in [4], Springer, Berlin, 1981, pp. 261–357.Google Scholar
[25] Pohlers, W., Cut elimination for impredicative infinitary systems, part I: Ordinal analysis of ID1 , Archiv für Mathematische Logik und Grundlagenforschung, vol. 21 (1981), pp. 69–87.Google Scholar
[26] Pohlers, W., Cut elimination for impredicative infinitary systems, part II: Ordinal analysis for iterated inductive definitions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 22 (1982), pp. 113–129.Google Scholar
[27] Pohlers, W., Proof theory and ordinal analysis, Archive for Mathematical Logic, vol. 30 (1991), pp. 311–376.Google Scholar
[28] Rathjen, M., An ordinal analysis of comprehension and related systems, in preparation.Google Scholar
[29] Rathjen, M., Proof-theoretic analysis of KPM, Archive for Mathematical Logic, vol. 30 (1991), pp. 377–403.Google Scholar
[30] Rathjen, M., How to develop proof–theoretic ordinal f unctions on the basis of admissible sets, Mathematical Quarterly, vol. 39 (1993), pp. 47–54.Google Scholar
[31] Rathjen, M., Collapsing functions based on recursively large ordinals: A well–ordering proof for KPM, Archive for Mathematical Logic, vol. 33 (1994), pp. 35–55.CrossRefGoogle Scholar
[32] Rathjen, M., Proof theory of reflection, Annals of Pure and Applied Logic, vol. 68 (1994), pp. 181–224.Google Scholar
[33] Richter, W. and Aczel, P., Inductive definitions and reflecting properties of admissible ordinals, Generalized recursion theory, North-Holland, Amsterdam, 1973, pp. 301–381.Google Scholar
[34] Schlüter, A., Provability in set theories with reflection, submitted.Google Scholar
[35] Schütte, K., Beweistheoretische Erfassung der unendlichen Induktion in der Zahlentheorie, Mathematische Annalen, vol. 122 (1951), pp. 369–389.Google Scholar
[36] Schütte, K., Beweistheorie, Springer-Verlag, Berlin, 1960.Google Scholar
[37] Schütte, K., Eine Grenze für die Beweisbarkeit der transfiniten Induktion in der verzweigten Typenlogik, Archiv für Mathematische Logik und Grundlagenforschung, vol. 67 (1964), pp. 45–60.CrossRefGoogle Scholar
[38] Schütte, K., Predicative well-orderings, Formal systems and recursive functions, North-Holland, 1965, pp. 176–184.Google Scholar
[39] Setzer, T., Proof theoretical strength of Martin-löf type theory with w-type and one universe, Thesis, University of Munich, 1993.Google Scholar
[40] Simpson, S., Nichtbeweisbarkeit von gewissen kombinatorischen Eigenschaften endlicher Bäume, Archiv für Mathematische Logik und Grundlagenforschung, vol. 25 (1985), pp. 45–65.Google Scholar
[41] Solovay, R. M., Reinhardt, W. N., and Kanamori, A., Strong axioms of infinity and elementary embeddings, Annals of Mathematical Logic, vol. 13 (1978), pp. 73–116.Google Scholar
[42] Takeuti, G., Consistency proofs of subsystems of classical analysis, Annals of Mathematics, vol. 86 (1967), pp. 299–348.Google Scholar
[43] Takeuti, G., Proof theory and set theory, Synthese, vol. 62 (1985), pp. 255–263.Google Scholar
[44] Takeuti, G. and Yasugi, M., The ordinals of the systems of second order arithmetic with the provably –comprehension and the –comprehension axiom respectively, Japanese Journal of Mathematics, vol. 41 (1973), pp. 1–67.CrossRefGoogle Scholar
[45] Woodin, H., Large cardinal axioms and independence: The continuum problem revisited, Mathematical Intelligencer, 1994, pp. 31–35.Google Scholar