Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-22T14:46:59.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Proper Forcing, Cardinal Arithmetic, and Uncountable Linear Orders

Published online by Cambridge University Press:  15 January 2014

Justin Tatch Moore
Justin Tatch Moore*
Affiliation:
Department of Mathematics, Boise State University, Boise, Idaho 83725, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper I will communicate some new consequences of the Proper Forcing Axiom. First, the Bounded Proper Forcing Axiom implies that there is a well ordering of ℝ which is Σ1-definable in (H(ω2), ϵ). Second, the Proper Forcing Axiom implies that the class of uncountable linear orders has a five element basis. The elements are X, ω1, 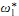, C, C * where X is any suborder of the reals of size ω1 and C is any Countryman line. Third, the Proper Forcing Axiom implies the Singular Cardinals Hypothesis at k unless stationary subsets of 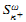reflect. The techniques are expected to be applicable to other open problems concerning the theory ofH(ω2).

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 11 , Issue 1 , March 2005 , pp. 51 - 60
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Abraham, U. and Shelah, S., Isomorphism types of Aronszajn trees, Israel Journal of Mathematics, vol. 50 (1985), no. 1–2, pp. 75–113.CrossRefGoogle Scholar
[2] Abraham, Uri, Rubin, Matatyahu, and Shelah, Saharon, On the consistency of some partition theorems for continuous colorings, and the structure of ℵ1 -dense real order types, Annals of Pure and Applied Logic, vol. 29 (1985), no. 2, pp. 123–206.CrossRefGoogle Scholar
[3] Bagaria, Joan, Bounded forcing axioms as principles of generic absoluteness, Archive for Mathematical Logic, vol. 39 (2000), no. 6, pp. 393–401.CrossRefGoogle Scholar
[4] Baumgartner, James E., All ℵ1-dense sets of reals can be isomorphic, Fundamenta Mathematicae, vol. 79 (1973), no. 2, pp. 101–106.CrossRefGoogle Scholar
[5] Bekkali, M., Topics in set theory, Springer-Verlag, Berlin, 1991, Lebesgue measurabil-ity, large cardinals, forcing axioms, ρ-functions, Notes on lectures by Stevo Todorčević.CrossRefGoogle Scholar
[6] Cummings, James and Schimmerling, Ernest, Indexed squares, Israel Journal of Mathematics, vol. 131 (2002), pp. 61–99.CrossRefGoogle Scholar
[7] Feng, Qi and Jech, Thomas, Projective stationary sets and a strong reflection principle, Journal of the London Mathematical Society. Second Series, vol. 58 (1998), no. 2, pp. 271–283.CrossRefGoogle Scholar
[8] Foreman, Matthew, Magidor, Menachem, and Shelah, Saharon, Martin's Maximum, saturated ideals, and nonregular ultrafilters. I, Annals of Mathematics. Second Series, vol. 127 (1988), no. 1, pp. 1–47.CrossRefGoogle Scholar
[9] Goldstern, Martin and Shelah, Saharon, The Bounded Proper Forcing Axiom, The Journal of Symbolic Logic, vol. 60 (1995), no. 1, pp. 58–73.CrossRefGoogle Scholar
[10] Gruenhage, Gary, Perfectly normal compacta, cosmic spaces, and some partition problems, Open problems in topology, North-Holland, Amsterdam, 1990, pp. 85–95.Google Scholar
[11] Moore, Justin Tatch, Set mapping reflection, submitted to Journal of Mathematical Logic in 11 2003.Google Scholar
[12] Moore, Justin Tatch, A five element basis for the uncountable linear orders, Preprint, 02 2004.Google Scholar
[13] Moore, Justin Tatch, The Proper Forcing Axiom, Prikry forcing, and the Singular Cardinals Hypothesis, Preprint, 07 2004.Google Scholar
[14] Shelah, Saharon, Decomposing uncountable squares to countably many chains, Journal of Combinatorial Theory Series A, vol. 21 (1976), no. 1, pp. 110–114.CrossRefGoogle Scholar
[15] Shelah, Saharon, On what I do not understand (and have something to say). I, Fundamenta Mathematicae, vol. 166 (2000), no. 1–2, pp. 1–82, Saharon Shelah's anniversary issue.CrossRefGoogle Scholar
[16] Shelah, Saharon, Reflection implies SCH, Preprint, 07 2004.Google Scholar
[17] Sierpinski, W., Sur unprobleme concernant les types de dimensions, Fundamenta Mathematicae, vol. 19 (1932), pp. 65–71.CrossRefGoogle Scholar
[18] Silver, Jack, On the singular cardinals problem, Proceedings of the International Congress of Mathematicians (Vancouver, B.C., 1974) (Montreal, Quebec), vol. 1, Canadian Mathematics Congress, 1975, pp. 265–268.Google Scholar
[19] Todorčević, Stevo, A note on the proper forcing axiom, Axiomatic set theory (Boulder, Colorado, 1983), Contempory Mathematicians, vol. 31, American Mathematical Society, Providence, RI, 1984, pp. 209–218.CrossRefGoogle Scholar
[20] Todorčević, Stevo, Partitioning pairs of countable ordinals, Acta Mathematica, vol. 159 (1987), no. 3–4, pp. 261–294.CrossRefGoogle Scholar
[21] Todorčević, Stevo, Partition problems in topology, American Mathematical Society, 1989.CrossRefGoogle Scholar
[22] Todorčević, Stevo, A classification of transitive relations on ω1 , Proceedings of the London Mathematical Society. Third Series, vol. 73 (1996), no. 3, pp. 501–533.CrossRefGoogle Scholar
[23] Todorčević, Stevo, Localized reflection and fragments of PFA, Logic and scientific methods, DI- MACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 259, American Mathematical Society, 1997, pp. 145–155.CrossRefGoogle Scholar
[24] Todorčević, Stevo, Basis problems in combinatorial set theory, Proceedings of the International Congress of Mathematicians, vol. II (Berlin, 1998), vol. II, 1998, Number Extra, pp. 43–52.CrossRefGoogle Scholar
[25] Todorčević, Stevo, Lipszhitz maps on trees, Technical Report 13, Institut Mittag-Leffler, 2000/2001.Google Scholar
[26] Todorčević, Stevo, Generic absoluteness and the continuum, Mathematical Research Letters, vol. 9 (2002), pp. 465–472.CrossRefGoogle Scholar
[27] Todorcevic, Stevo, Coherent sequences, North-Holland, (in preparation).Google Scholar
[28] Velickovic, Boban, Forcing axioms and stationary sets, Advances in Mathematics, vol. 94 (1992), no. 2, pp. 256–284.CrossRefGoogle Scholar
[29] Woodin, W. Hugh, The axiom of determinacy, forcing axioms, and the non-stationary ideal, Logic and its Applications, de Gruyter, 1999.CrossRefGoogle Scholar