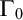1 Introduction
1.1. What predicativism, and why?
In [Reference Shapiro44] the basic historic problem of the research in foundations of mathematics (FOM) is formulated as follows:
How to reconstruct mathematics on a secure basis, one maximally immune to rational doubts.
The predicativist program [Reference Crosilla, Jaeger and Sieg11, Reference Crosilla, Mainzer, Schuster and Schwichtenberg12, Reference Feferman and Shapiro24, Reference Weaver49, Reference Weaver51] has been one of the attempts to solve this basic problem of FOM. It seeks to establish certainty in mathematics without revolutionizing it or changing its underlying classical logic (as the intuitionistic program does). The program was initiated by Poincaré [Reference Poincaré36–Reference Poincaré39]. Its viability was demonstrated by Weyl, who seriously developed it for the first time in his famous small book “Das Kontinuum” [Reference Weyl52, Reference Weyl, Pollard and Bole54]. Weyl, and then Feferman [Reference Feferman22, Reference Feferman25], have shown that a very large part of classical analysis can be developed within their predicative systems. Feferman further argued that predicative mathematics in fact suffices for developing all the mathematics that is actually indispensable to present-day natural sciences. Hence the predicativist program has been successful in solving the basic problem of FOM. (In my opinion it is the only one about which this can truly be said.)
Poincaré’s predicativism started as a reaction to the set-theoretical paradoxes. However, in the writings of both Poincaré and Weyl, predicativity derives not so much from the need to avoid paradoxes, but from their definitionist view that infinite objects, such as sets or functions, exist only in so far as they are introduced through legitimate definitions:
“No one can describe an infinite set other than by indicating properties which are characteristic of the elements of the set. And no one can establish a correspondence among infinitely many things without indicating a rule, i.e., a relation, which connects the corresponding objects with one another. The notion that an infinite set is a ‘gathering’ brought together by infinitely many individual arbitrary acts of selection, assembled and then surveyed as a whole by consciousness, is nonsensical.” [Reference Weyl, Pollard and Bole54, p. 23]
The implications of the above principle concerning infinite objects depend of course in a crucial way on the question: What definitions should be accepted as ‘legitimate’? Therefore it is no wonder that ‘predicativism’ (like ‘constructivism’) becomes a name of a group of approaches to mathematics and its foundations [Reference Crosilla, Mainzer, Schuster and Schwichtenberg12, Reference Feferman and Shapiro24].Footnote
1
We emphasize that in this paper we reserve this name solely to the program as it was initiated by Poincaré and pursued by Weyl. That program is known nowadays as ‘predicativity given the natural numbers’, since in addition to the definitionist principle mentioned above, it also accepts the collection
![]() $\mathcal {N}$
of the natural numbers as a well understood mathematical concept that constitutes a set. Moreover, it views the idea of iterating an operation or a relation a finite number of times as fundamental, and accepts induction on the natural numbers as a universally valid method of proof.Footnote
2
Still, even with this restriction, the word ‘predicative’ has two different interpretations, corresponding to Poincaré’s “two distinct diagnoses of the source of the paradoxes” ([Reference Feferman and Shapiro24]; see also [Reference Crosilla, Jaeger and Sieg11]). We call them ‘Russell’s predicativity’ and ‘Poincaré–Weyl predicativity’. This paper is devoted to the second one. However, since it is the first which is usually identified with predicativism, we discuss it first.
$\mathcal {N}$
of the natural numbers as a well understood mathematical concept that constitutes a set. Moreover, it views the idea of iterating an operation or a relation a finite number of times as fundamental, and accepts induction on the natural numbers as a universally valid method of proof.Footnote
2
Still, even with this restriction, the word ‘predicative’ has two different interpretations, corresponding to Poincaré’s “two distinct diagnoses of the source of the paradoxes” ([Reference Feferman and Shapiro24]; see also [Reference Crosilla, Jaeger and Sieg11]). We call them ‘Russell’s predicativity’ and ‘Poincaré–Weyl predicativity’. This paper is devoted to the second one. However, since it is the first which is usually identified with predicativism, we discuss it first.
1.2 Russell’s predicativity
Adopting the analysis indicated in Richard’s paper [Reference Richard40], Poincaré’s first diagnosis was that the definition of Richard’s paradoxical real number is circular: it uses the totality of all definitions, to which it already belongs. The corresponding Vicious Circle Principle, VCP, was adopted by Russel in [Reference Russell41] and in Principia Mathematica [Reference Whitehead and Russell55]. According to the latter, a vicious circle arises when we assume that “a collection of objects may contain members which can only be defined in terms of the collection itself”.Footnote 3 A clearer (and stronger) formulation of the VCP has been given by Kreisel in [Reference Kreisel30]:
“A predicative definition of a set (say, of natural numbers) is required to use quantification only over ‘previously defined’ totalities; the set of natural numbers themselves is supposed to be given, or the notion of ‘finite’ is supposed to be well-defined.”
Kreisel then went on and note that
“The traditional way of making the idea of a predicative definition explicit is by introducing a ramified hierarchy.”
The idea of ramified hierarchy was introduced and used by Russell in Principia Mathematica. Later it was generalized by Wang [Reference Wang48] and Kreisel. In the second-order context the generalization is explained in [Reference Feferman and Shapiro24] as follows:
“The basic step in that hierarchy consists in passing from a collection D of subsets of
![]() $\mathcal {N}$
to a new collection
$\mathcal {N}$
to a new collection
![]() $D^\star $
by putting a set S in
$D^\star $
by putting a set S in
![]() $D^\star $
just in case there is a formula
$D^\star $
just in case there is a formula
![]() $\varphi (x)$
of second-order arithmetic such that for all n,
$\varphi (x)$
of second-order arithmetic such that for all n,
![]() $n\in S\leftrightarrow (\varphi (n))^D,$
where the superscript ‘D’ indicates that all second-order quantifiers in
$n\in S\leftrightarrow (\varphi (n))^D,$
where the superscript ‘D’ indicates that all second-order quantifiers in
![]() $\varphi $
are relativized to range over D. Then we can define the collections
$\varphi $
are relativized to range over D. Then we can define the collections
![]() $R_\alpha $
for arbitrary ordinals
$R_\alpha $
for arbitrary ordinals
![]() $\alpha $
by
$\alpha $
by
![]() $R_0=\emptyset , R_{\alpha +1}=(R_\alpha )^\star , \mbox { and for limit } \alpha , R_\alpha =\bigcup _{\beta <\alpha }R_\beta $
.”
$R_0=\emptyset , R_{\alpha +1}=(R_\alpha )^\star , \mbox { and for limit } \alpha , R_\alpha =\bigcup _{\beta <\alpha }R_\beta $
.”
This description raises the question: What ordinals
![]() $\alpha $
can serve for the purpose of constructing this ramified hierarchy of
$\alpha $
can serve for the purpose of constructing this ramified hierarchy of
![]() $R_{\alpha }$
s? To answer this, Kreisel proposed in [Reference Kreisel29] an autonomous process, where a well-ordering becomes available at some stage only if it has been defined and recognized (as a well-ordering of
$R_{\alpha }$
s? To answer this, Kreisel proposed in [Reference Kreisel29] an autonomous process, where a well-ordering becomes available at some stage only if it has been defined and recognized (as a well-ordering of
![]() $\omega $
) at an earlier stage. Without the ‘recognition’ criterion, which introduces proof-theoretic considerations, we are left with a purely semantic condition that allows to go up to every well-ordering
$\omega $
) at an earlier stage. Without the ‘recognition’ criterion, which introduces proof-theoretic considerations, we are left with a purely semantic condition that allows to go up to every well-ordering
![]() $<\omega _1^{CK}$
(Church–Kleene’s first non-recursive ordinal). With the recognition condition, Feferman [Reference Feferman15] and Schütte [Reference Schütte, Crossley and Dummett42] independently replaced
$<\omega _1^{CK}$
(Church–Kleene’s first non-recursive ordinal). With the recognition condition, Feferman [Reference Feferman15] and Schütte [Reference Schütte, Crossley and Dummett42] independently replaced
![]() $\omega _1^{CK}$
by the much smaller
$\omega _1^{CK}$
by the much smaller
![]() $\Gamma _0$
(the Feferman–Schütte ordinal). Following their work, the hierarchies of formal systems up to
$\Gamma _0$
(the Feferman–Schütte ordinal). Following their work, the hierarchies of formal systems up to
![]() $\Gamma _0$
which were developed by them (on the basis of the intuitive semantics of the
$\Gamma _0$
which were developed by them (on the basis of the intuitive semantics of the
![]() $R_{\alpha }$
s) have become the “canonical reference: one considers predicative any formal system which can be reduced to a system in that hierarchy” [Reference Crosilla, Jaeger and Sieg11]. Accordingly,
$R_{\alpha }$
s) have become the “canonical reference: one considers predicative any formal system which can be reduced to a system in that hierarchy” [Reference Crosilla, Jaeger and Sieg11]. Accordingly,
![]() $\Gamma _0$
is almost universally accepted as the ‘ordinal of predicativity’. An example of the implications of this is given in [Reference Crosilla, Oliveri, Ternullo and Boscolo13]: “The fact that the proof-theoretic strength of theories of inductive definitions exceeds the strength of the whole ramified hierarchy is taken as clear indication that generalized inductive definitions involve impredicativity.”
$\Gamma _0$
is almost universally accepted as the ‘ordinal of predicativity’. An example of the implications of this is given in [Reference Crosilla, Oliveri, Ternullo and Boscolo13]: “The fact that the proof-theoretic strength of theories of inductive definitions exceeds the strength of the whole ramified hierarchy is taken as clear indication that generalized inductive definitions involve impredicativity.”
Up to now, the only mathematician to reject the ‘
![]() $\Gamma _0$
-thesis’ has been Weaver, who forcefully attacked this thesis in [Reference Weaver50]. Unfortunately, his (in my opinion quite justified) criticism of the various justifications given by Feferman for this thesis has been almost totally ignored by the logical community. Nevertheless, as a true predicativist (which is what I am taking myself to be), it is clear to me that the identification of predicativity with the ramified systems of Feferman and Schütte cannot be correct. A first, very simple, problem with it is that no predicativist (and for that matter—no mathematician) thinks in terms of ramified systems. Moreover, Feferman admits that “ramified theories are unsuitable as a framework for the development of analysis” [Reference Feferman and Shapiro24]. Another problem, that was repeatedly noted by Feferman himself, is that the general notions of well-ordering and ordinal on which they are based are not predicatively acceptable.Footnote
4
Third, and most important: just the description and understanding of the ramified hierarchy rely on principles that are not included in the theories in [Reference Feferman15] and [Reference Schütte43] which are based on this hierarchy. This is rather clear in case
$\Gamma _0$
-thesis’ has been Weaver, who forcefully attacked this thesis in [Reference Weaver50]. Unfortunately, his (in my opinion quite justified) criticism of the various justifications given by Feferman for this thesis has been almost totally ignored by the logical community. Nevertheless, as a true predicativist (which is what I am taking myself to be), it is clear to me that the identification of predicativity with the ramified systems of Feferman and Schütte cannot be correct. A first, very simple, problem with it is that no predicativist (and for that matter—no mathematician) thinks in terms of ramified systems. Moreover, Feferman admits that “ramified theories are unsuitable as a framework for the development of analysis” [Reference Feferman and Shapiro24]. Another problem, that was repeatedly noted by Feferman himself, is that the general notions of well-ordering and ordinal on which they are based are not predicatively acceptable.Footnote
4
Third, and most important: just the description and understanding of the ramified hierarchy rely on principles that are not included in the theories in [Reference Feferman15] and [Reference Schütte43] which are based on this hierarchy. This is rather clear in case
![]() $\alpha $
is a limit ordinal:
$\alpha $
is a limit ordinal:
![]() $R_{\alpha }$
is actually defined in this case as
$R_{\alpha }$
is actually defined in this case as
![]() $\bigcup \{R(x)\mid x\in \{\beta \mid \beta <\alpha \}\}$
. Hence it is based on accepting at least some instances of ZF’s axioms of union and replacement. However, if we let
$\bigcup \{R(x)\mid x\in \{\beta \mid \beta <\alpha \}\}$
. Hence it is based on accepting at least some instances of ZF’s axioms of union and replacement. However, if we let
![]() $R_0=\mathcal {N}$
(which is the predicativist natural starting point, rather then
$R_0=\mathcal {N}$
(which is the predicativist natural starting point, rather then
![]() $R_0=\emptyset $
), then similar problems exist even if we do not use transfinite ordinals, but only the natural numbers (as Russell did). Thus already in constructing elements of
$R_0=\emptyset $
), then similar problems exist even if we do not use transfinite ordinals, but only the natural numbers (as Russell did). Thus already in constructing elements of
![]() $R_2$
we allow quantification over
$R_2$
we allow quantification over
![]() $R_1$
. This should mean that
$R_1$
. This should mean that
![]() $R_1$
is taken as a “complete totality”. But
$R_1$
is taken as a “complete totality”. But
![]() $R_1$
is not obtained using just “quantification only over previously defined totalities”, and it is actually unclear what
$R_1$
is not obtained using just “quantification only over previously defined totalities”, and it is actually unclear what
![]() $R_1$
is at the first place. Usually it is identified with the collection (set?) of arithmetical subsets of
$R_1$
is at the first place. Usually it is identified with the collection (set?) of arithmetical subsets of
![]() $\mathcal {N}$
. If so, then each element of
$\mathcal {N}$
. If so, then each element of
![]() $R_1$
is indeed obtained using just quantification only over
$R_1$
is indeed obtained using just quantification only over
![]() $\mathcal {N}$
. But this does not mean that so is
$\mathcal {N}$
. But this does not mean that so is
![]() $R_1$
itself. (For example, if we identify ordinals with von Neumann’s ordinals, then
$R_1$
itself. (For example, if we identify ordinals with von Neumann’s ordinals, then
![]() $\Gamma _0$
is not predicatively definable according to the
$\Gamma _0$
is not predicatively definable according to the
![]() $\Gamma _0$
-thesis, even though each element of
$\Gamma _0$
-thesis, even though each element of
![]() $\Gamma _0$
is.) In fact, the only reasonable definition of the collection of arithmetical sets I can think of is the following:
$\Gamma _0$
is.) In fact, the only reasonable definition of the collection of arithmetical sets I can think of is the following:
where True is the set of true sentences in the first-order language of PA, and
![]() $predicate(n)$
means that n is a formula with exactly one free variable. (As usual, we identify here a formula with its Gödel number.) However, this definition relies on the availability of the set True, which is not arithmetical. It follows that if
$predicate(n)$
means that n is a formula with exactly one free variable. (As usual, we identify here a formula with its Gödel number.) However, this definition relies on the availability of the set True, which is not arithmetical. It follows that if
![]() $R_1$
is the collection of arithmetical sets then it can only be defined using a set that at best belongs to some
$R_1$
is the collection of arithmetical sets then it can only be defined using a set that at best belongs to some
![]() $R_i$
such that
$R_i$
such that
![]() $i>1$
, and so is defined in terms of
$i>1$
, and so is defined in terms of
![]() $R_1$
. This is obviously circular. To construct the ramified hierarchy we have therefore either to accept in addition to
$R_1$
. This is obviously circular. To construct the ramified hierarchy we have therefore either to accept in addition to
![]() $\mathcal {N}$
infinitely many other sets as ‘given’ to us, or to realize that some hidden predicatively acceptable principles are involved already in the passage from
$\mathcal {N}$
infinitely many other sets as ‘given’ to us, or to realize that some hidden predicatively acceptable principles are involved already in the passage from
![]() $\mathcal {N}$
to
$\mathcal {N}$
to
![]() $R_1$
. The first option completely goes against the central ideas of Poincaré and Weyl. So we are left with the second.
$R_1$
. The first option completely goes against the central ideas of Poincaré and Weyl. So we are left with the second.
Note 1.1. A close inspection shows that in general, the passage from D to
![]() $D^\star $
implicitly involves accepting two principles:
$D^\star $
implicitly involves accepting two principles:
-
• One may use the model-theoretic operation that associates with any formula
 $\varphi (x)$
of second-order arithmetic the set
$\varphi (x)$
of second-order arithmetic the set
 $\{n\in N\mid N\models (\varphi (n))^D\}$
.
$\{n\in N\mid N\models (\varphi (n))^D\}$
. -
• One may take as predicatively valid the instance of the replacement axiom that allows us to construct the image of this model-theoretic operation.
Note 1.2. There are some other indications that the ‘
![]() $\Gamma _0$
-thesis’ might be wrong.
$\Gamma _0$
-thesis’ might be wrong.
-
• A system T which is proof-theoretically reducible to
 $\bigcup _{\alpha <\Gamma _0} R_{\alpha }$
is called in the literature ‘locally predicative’. About such T Feferman wrote in [Reference Feferman and Shapiro24]:An important example of a ‘locally predicative’ system is
$\bigcup _{\alpha <\Gamma _0} R_{\alpha }$
is called in the literature ‘locally predicative’. About such T Feferman wrote in [Reference Feferman and Shapiro24]:An important example of a ‘locally predicative’ system isThough the system T as a whole may not be justifiable predicatively, each theorem
 $\varphi $
of T rests on predicative grounds, at least indirectly. In practice, more can be said: T is conservative over the autonomous ramified progression for arithmetic sentences, i.e., if
$\varphi $
of T rests on predicative grounds, at least indirectly. In practice, more can be said: T is conservative over the autonomous ramified progression for arithmetic sentences, i.e., if
 $\varphi $
is arithmetical and provable in T then it is provable in that progression. For second-order T this can often be strengthened to conservativity for
$\varphi $
is arithmetical and provable in T then it is provable in that progression. For second-order T this can often be strengthened to conservativity for
 $\Pi _1^1$
-sentences.
$\Pi _1^1$
-sentences. $\mathbf {AT\!R}_0$
, which is one of the ‘big five’ theories which were studied in reverse mathematics [Reference Simpson46].
$\mathbf {AT\!R}_0$
, which is one of the ‘big five’ theories which were studied in reverse mathematics [Reference Simpson46].
 $\mathbf {AT\!R}_0$
is indeed conservative over
$\mathbf {AT\!R}_0$
is indeed conservative over
 $\bigcup _{\alpha <\Gamma _0} R_{\alpha }$
for
$\bigcup _{\alpha <\Gamma _0} R_{\alpha }$
for
 $\Pi _1^1$
-sentences, and its proof-theoretical ordinal is
$\Pi _1^1$
-sentences, and its proof-theoretical ordinal is
 $\Gamma _0$
. In contrast, the proof-theoretical ordinal of the full theory
$\Gamma _0$
. In contrast, the proof-theoretical ordinal of the full theory
 $\mathbf {ATR}$
is the much bigger
$\mathbf {ATR}$
is the much bigger
 $\Gamma _{\!\epsilon _0}$
. Hence the
$\Gamma _{\!\epsilon _0}$
. Hence the
 $\Gamma _0$
-thesis implies that
$\Gamma _0$
-thesis implies that
 $\mathbf {ATR}$
is not locally predicative. But the only difference between
$\mathbf {ATR}$
is not locally predicative. But the only difference between
 $\mathbf {AT\!R}$
and
$\mathbf {AT\!R}$
and
 $\mathbf {AT\!R}_0$
is that the single induction axiom of the latter is replaced in the former by the full induction schema. However, the induction schema is universally accepted as being predicatively justified, and is actually included in the finitary systems of [Reference Feferman15]. Therefore at least the arithmetical theorems of
$\mathbf {AT\!R}_0$
is that the single induction axiom of the latter is replaced in the former by the full induction schema. However, the induction schema is universally accepted as being predicatively justified, and is actually included in the finitary systems of [Reference Feferman15]. Therefore at least the arithmetical theorems of
 $\mathbf {AT\!R}$
might be viewed as no less predicatively justified than those of
$\mathbf {AT\!R}$
might be viewed as no less predicatively justified than those of
 $\mathbf {AT\!R}_0$
.
$\mathbf {AT\!R}_0$
.
-
• In the conclusion of [Reference Pohlers, Kahle and Rathjen35], Pohlers made the following observation:
Pohlers went then on and suggested a line of investigation that (at least according to my understanding) leads to predicativity beyondThe studies in the present paper lead to the suspicion that the role of
 $\Gamma _0$
as the limit of predicativity might not depend on deep philosophical but rather on technical reasons.
$\Gamma _0$
as the limit of predicativity might not depend on deep philosophical but rather on technical reasons. $\Gamma _0$
.
$\Gamma _0$
.
1.3 Poincaré and Weyl’s view of predicativity as invariance
As noted above, a notion of predicativity which is quite different from the Russellian one was introduced by Poincaré in [Reference Poincaré38]. This was particularly emphasized in [Reference Crosilla, Jaeger and Sieg11]:
“For Poincare impredicative definitions are problematic as they treat as completed infinite classes which are instead open-ended or incomplete by their very nature. Predicative definitions, instead, guarantee that the classes so defined are stable and invariant.”
In Poincaré own words:
“Hence a distinction between two species of classifications, which are applicable to the elements of infinite collections: the predicative classifications, which cannot be disordered by the introduction of new elements; the non predicative classifications, which are forced to remain without end by the introduction of new elements.”
This view of predicativity underlies Weyl’s great work in [Reference Weyl52]. A careful reading (see [Reference Adams and Luo2, Reference Avron6]) of this book and of related papers of Weyl on the subject shows that predicativity as invariance is based in his work on the following principles:Footnote 5
-
1. Sets are ‘produced’ genetically, that is, from applying legitimate operations to sets which are accepted as basic, or had previously been produced.
“If we imagine, as is appropriate for an intuitive understanding, that the relations and corresponding sets are ‘produced’ genetically, then this production will …occur in merely parallel individual acts (so to speak).” [Reference Weyl, Pollard and Bole54, p. 40]
-
2. Accordingly, the elements of a set are logically prior to that set.
-
3. Sets are extensional, and the identity of a set is fully determined by the identity of its elements—sets that have the same elements are identical.
-
4. There is no single, complete intended universe V of sets. The ‘universe of sets’ is created in stages, and is always open and growing. To each stage corresponds what Weyl called a sphere of operation (i.e., a definite universe of sets equipped with some (finite) collection of predicates and operations) in which terms and formulas take values.
On the other hand (and in contrast):“Thus, contrary to Cantor’s proposal, no universal scale of infinite ordinal and cardinal numbers applicable to every sphere of operation can exist.” [Reference Weyl, Pollard and Bole54, p. 24]
“The numbers can (in any sphere of operation) be used to determine the cardinality of sets.” [Reference Weyl, Pollard and Bole54, p. 55]
-
5. The current sphere of operation may be expanded in the future, e.g., by introducing new legitimate methods of defining sets, which in turn might produce new sets. The truth values of formulas may then be changed.
“If we regard the principles of definition as an ‘open’ system, i.e., if we reserve the right to extend them when necessary by making additions, then in general the question of whether a given function is continuous must also remain open (though we may attempt to resolve any delimited question). For a function which, within our current system, is continuous can lose this property if our principles of definition are expanded and, accordingly, the real numbers ‘presently’ available are joined by others.” [Reference Weyl, Pollard and Bole54, p. 87]
-
6. Values of terms and truth-values of formulas are always evaluated with respect to some definite sphere of operation—never with respect to the whole open ‘universe of sets’. Hence classical logic is accepted as valid. For example,
 $\neg \varphi \vee \varphi $
is valid in any sphere of operation, even though the truth value of
$\neg \varphi \vee \varphi $
is valid in any sphere of operation, even though the truth value of
 $\varphi $
may change when the current sphere of operation is expanded.
$\varphi $
may change when the current sphere of operation is expanded. -
7. In contrast, the identity of already existing objects (and so the value of terms) should remain the same even if the current sphere of operation is expanded. Accordingly, a definition of an object is legitimate (or ‘predicative’) if, and only if, the identity of the object it defines is invariant under extension. (Because of this principle, there are certain constraints in Weyl’s system on the use of quantification in definitions. However, there are no constrains in that system on the use of quantifiers in building formulas.) Weyl called an object so defined “a definite, self-existent object”. Similarly, a definition of an operation is legitimate if the results of its applications depend only on the identity of the arguments, but not on the specific sphere of operation in which the application is made.
-
8. Any theory we develop should be true not only in the current sphere of operation, but in any future one. Hence our current theories impose constraints on future spheres of operation. Accordingly, expanding our spheres of operation and extending our theories are done simultaneously. Moreover:
“Our principles for the formation of derived relations can be formulated as axioms concerning sets and functions; and, in fact, mathematics will proceed in such a way that it draws the logical consequences of these axioms.” [Reference Weyl, Pollard and Bole54, p. 44]
-
9. The predicates of elementhood (
 $\in $
) and equality (=) are basic.
$\in $
) and equality (=) are basic. -
10. Using ramification in definitions, or classifying sets according to ‘levels’, should be avoided.
“The temptation to pass beyond the first level of construction must be resisted; instead, one should try to make the range of constructible relations as wide as possible by enlarging the stock of basic operations.” [Reference Weyl53]
It should be emphasized that according to the last quotation, Principle 10 is not due just to the inconvenience which is caused by using ramified systems. There is also a direct conflict between the Russellian approach and Weyl’s approach. The former is implicitly based on the view that there are no predicatively legitimate methods of defining subsets of
![]() $\mathcal {N}$
beyond those that are allowed in the construction of the hierarchy of
$\mathcal {N}$
beyond those that are allowed in the construction of the hierarchy of
![]() $R_{\alpha }$
s. This view entails that the union of the
$R_{\alpha }$
s. This view entails that the union of the
![]() $R_{\alpha }$
s includes all the predicatively acceptable subsets of
$R_{\alpha }$
s includes all the predicatively acceptable subsets of
![]() $\mathcal {N}$
. In contrast, already the collection of first-level subsets of
$\mathcal {N}$
. In contrast, already the collection of first-level subsets of
![]() $\mathcal {N}$
is an open collection according to Weyl’s view. Hence it may always be extended “by enlarging the stock of basic operations”. Weyl indeed did just that when he added the very important operation of iteration to this stock. As discovered by Feferman in [Reference Feferman, Cellucci and Sambin20], this operation makes it possible to define non-arithmetical subsets of
$\mathcal {N}$
is an open collection according to Weyl’s view. Hence it may always be extended “by enlarging the stock of basic operations”. Weyl indeed did just that when he added the very important operation of iteration to this stock. As discovered by Feferman in [Reference Feferman, Cellucci and Sambin20], this operation makes it possible to define non-arithmetical subsets of
![]() $\mathcal {N}$
. Hence Weyl recognized as first-level subsets of
$\mathcal {N}$
. Hence Weyl recognized as first-level subsets of
![]() $\mathcal {N}$
sets that do not belong to what is called above
$\mathcal {N}$
sets that do not belong to what is called above
![]() $R_1$
!Footnote
6
$R_1$
!Footnote
6
Note 1.3. Actually, the invariance criterion has been used by Feferman too in some of his unramified systems. Thus, IR, the first of the two unramified second-order locally predicative systems which were given in [Reference Feferman15], uses the Hyperarithmetic Comprehension Rule
![]() $\Delta _1^1$
-CR. This is justified in [Reference Feferman and Shapiro24] as follows:
$\Delta _1^1$
-CR. This is justified in [Reference Feferman and Shapiro24] as follows:
“The motivation for
![]() $\Delta _1^1$
-CR is the recognizable absoluteness (or invariance) of provably
$\Delta _1^1$
-CR is the recognizable absoluteness (or invariance) of provably
![]() $\Delta _1^1$
definitions, in the following sense. At each stage one has recognized certain closure conditions on the ‘open’ universe of sets, and the definitions
$\Delta _1^1$
definitions, in the following sense. At each stage one has recognized certain closure conditions on the ‘open’ universe of sets, and the definitions
![]() $D(x)$
of sets introduced at the next stage should be independent of what further closure conditions may be accepted. In the words of Poincaré, the definitions used of objects in an incomplete totality should not be “disturbed by the introduction of new elements.” Thus if U represents a universe of sets (subsets of
$D(x)$
of sets introduced at the next stage should be independent of what further closure conditions may be accepted. In the words of Poincaré, the definitions used of objects in an incomplete totality should not be “disturbed by the introduction of new elements.” Thus if U represents a universe of sets (subsets of
![]() $\mathcal {N}$
) satisfying given closure conditions and is extended to
$\mathcal {N}$
) satisfying given closure conditions and is extended to
![]() $S^\prime $
(satisfying the same closure conditions and possibly further ones) one wants D to be provably invariant or absolute in the sense that
$S^\prime $
(satisfying the same closure conditions and possibly further ones) one wants D to be provably invariant or absolute in the sense that
![]() $(\forall x)[D^U(x)\leftrightarrow D^{U^\prime }(x)]$
. This requirement is easily seen to hold for provably
$(\forall x)[D^U(x)\leftrightarrow D^{U^\prime }(x)]$
. This requirement is easily seen to hold for provably
![]() $\Delta _1^1$
formulas D.”
$\Delta _1^1$
formulas D.”
This passage contains a rather accurate description of the invariance criterion. However, it provides no explanation how it is connected with the Russellian approach, on which Feferman’s ramified systems are based.
1.4 Predicative set theories: Why and how
1.4.1 Why
Feferman’s systems (and to a lesser degree also Weyl’s system in [Reference Weyl52], as formalized in [Reference Avron6]) have one big drawback: they are practically inaccessible to the majority of the mathematical community. We believe that the major reason for this is that those systems do not use the framework of axiomatic set theory, which is almost universally accepted as the basic framework that provides the foundations of mathematics. What is more: Feferman’s systems are by far more complicated in comparison to impredicative axiomatic set theories like ZF, which are currently used for developing the whole of present day mathematics.
Another reason to prefer the set-theoretical framework is that some of its principles are anyway underlying the constructions on which the second-order ramified systems of Feferman and Schütte are based. Thus we have seen in Section 1.2 that the construction of the hierarchy of
![]() $R_\alpha $
s uses instances of the union and replacement axioms of
$R_\alpha $
s uses instances of the union and replacement axioms of
![]() $\mathbf {ZF}$
. But in what cases is such a use predicatively justified? It seems to me that developing predicative set theories is the only way to answer such questions. What is more, the notion of ordinal, which is crucial for the ramified systems but is also very problematic in their context, is not problematic at all in the set-theoretical one (assuming that the
$\mathbf {ZF}$
. But in what cases is such a use predicatively justified? It seems to me that developing predicative set theories is the only way to answer such questions. What is more, the notion of ordinal, which is crucial for the ramified systems but is also very problematic in their context, is not problematic at all in the set-theoretical one (assuming that the
![]() $\in $
-relation is well-foundedFootnote
7
). In the latter, one can use the notion of von Neumann ordinals, and those are defined by a simple, absolute formula.
$\in $
-relation is well-foundedFootnote
7
). In the latter, one can use the notion of von Neumann ordinals, and those are defined by a simple, absolute formula.
Finally, it is worth noting that predicativism was born as a reaction to the set-theoretical paradoxes, and was intended to provide a satisfactory solution to them. So (at least in my opinion) it should be most natural to develop predicative mathematics in the framework in which it has started.
Note 1.4. Locally predicative (in the sense of being proof-theoretically reducible to the systems of [Reference Feferman15]) set theories have already been introduced by Feferman in [Reference Feferman16, Reference Feferman, Scott and Jech18]. We shall say more about them in Section 4.4.
1.4.2 How
In the case of pure set theories, the main principle of the predicativity as invariance view of Poincaré and Weyl can be expressed as follows: a set exists if and only if can be determined by an invariant definition. Accordingly, the main two features of the system
![]() $\mathbf {PW}$
which is developed in the sequel are:
$\mathbf {PW}$
which is developed in the sequel are:
-
(I) Any existence claim which is made in one of those axioms of
 $\mathbf {PW}$
whose purpose is to allow the expansion of the sphere of operation is actually an existence and uniqueness claim. In other words, positive occurrences of the quantifier
$\mathbf {PW}$
whose purpose is to allow the expansion of the sphere of operation is actually an existence and uniqueness claim. In other words, positive occurrences of the quantifier
 $\exists $
in such an axiom are in the form
$\exists $
in such an axiom are in the form
 $\exists !$
. (This, of course, rules out the axiom of choice, as well as the axiom of
$\exists !$
. (This, of course, rules out the axiom of choice, as well as the axiom of
 $\Delta _0$
-collection of Kripke–Platek set theory as given in [Reference Barwise9].)
$\Delta _0$
-collection of Kripke–Platek set theory as given in [Reference Barwise9].) -
(II) Following Principles 1 and 7 in Section 1.3, any definition of a set which is made in
 $\mathbf {PW}$
is invariant. This is ensured by employing a syntactically defined invariance relation
$\mathbf {PW}$
is invariant. This is ensured by employing a syntactically defined invariance relation
 $\succ $
between formulas and finite sets of variables. The intended meaning of “
$\succ $
between formulas and finite sets of variables. The intended meaning of “
 $\varphi (x_1,\ldots \!,\! x_n,y_1,\ldots \!,\! y_k)\succ \{x_1,\ldots \!,\! x_n\}$
” is: “The identity of
$\varphi (x_1,\ldots \!,\! x_n,y_1,\ldots \!,\! y_k)\succ \{x_1,\ldots \!,\! x_n\}$
” is: “The identity of
 $\{\langle x_1,\ldots \!,\! x_n \rangle \mid \varphi \}$
is invariant: it depends only on the values assigned to
$\{\langle x_1,\ldots \!,\! x_n \rangle \mid \varphi \}$
is invariant: it depends only on the values assigned to
 $y_1,\ldots \!,\! y_k$
, but not on the surrounding universe”.Footnote
8
$y_1,\ldots \!,\! y_k$
, but not on the surrounding universe”.Footnote
8
Note 1.5. Principle (I) is not applicable to general validities like logically valid formulas or instances of
![]() $\in $
-induction. A trivial example is given by
$\in $
-induction. A trivial example is given by
![]() $\forall x\neg \varphi \vee \exists x\varphi $
, where
$\forall x\neg \varphi \vee \exists x\varphi $
, where
![]() $\varphi $
is arbitrary. In general, theorems of
$\varphi $
is arbitrary. In general, theorems of
![]() $\mathbf {PW}$
of this sort cannot be used for introducing new sets, or for providing absolute identification of existing ones.
$\mathbf {PW}$
of this sort cannot be used for introducing new sets, or for providing absolute identification of existing ones.
The following other important features of
![]() $\mathbf {PW}$
also directly correspond to the principles of Weyl and Poincaré that were described in Section 1.3:
$\mathbf {PW}$
also directly correspond to the principles of Weyl and Poincaré that were described in Section 1.3:
-
1. Like in ZF, and unlike in the systems of Weyl and Feferman, our system has a single type (or ‘category’, in Weyl’s terminology) of objects: sets. (This partially corresponds to Principle 10 in Section 1.3.)
-
2. Like in most of Feferman’s systems,
 $\mathbf {PW}$
is practically not really a single theory, but involves many theories, all of them first-order. In each stage of working within it, we do have a single theory T, but we have two options how to proceed: We may simply derive new theorems in T, but we may also move to a strictly stronger theory
$\mathbf {PW}$
is practically not really a single theory, but involves many theories, all of them first-order. In each stage of working within it, we do have a single theory T, but we have two options how to proceed: We may simply derive new theorems in T, but we may also move to a strictly stronger theory
 $\mathbf {T}^\star $
in an expanded language.Footnote
9
(This feature of
$\mathbf {T}^\star $
in an expanded language.Footnote
9
(This feature of
 $\mathbf {PW}$
implements Principles 4, 5, and 8 in Section 1.3.)
$\mathbf {PW}$
implements Principles 4, 5, and 8 in Section 1.3.) -
3. The logic of all theories in
 $\mathbf {PW}$
is classical logic (Principle 6 in Section 1.3).
$\mathbf {PW}$
is classical logic (Principle 6 in Section 1.3). -
4. The initial language of the system includes just two predicate symbols:
 $=$
and
$=$
and
 $\in $
(Principle 9 in Section 1.3) and a constant
$\in $
(Principle 9 in Section 1.3) and a constant
 $\omega $
for the set of natural numbers (taken to be the finite von Neumann ordinals). The inclusion of the latter is actually not essential, but it reflects well the central place that the natural numbers have in the predicativism of Poincaré and Weyl.
$\omega $
for the set of natural numbers (taken to be the finite von Neumann ordinals). The inclusion of the latter is actually not essential, but it reflects well the central place that the natural numbers have in the predicativism of Poincaré and Weyl. -
5. The following axiom and axiom schemas are included in all theories in
 $\mathbf {PW}$
:
$\mathbf {PW}$
:-
• The axiom of extensionality (Principle 3 in Section 1.3).
-
• Comprehension for invariant formulas (Principle 7 in Section 1.3).
-
•
 $\in $
-induction (which implements the vague Principle 2 in Section 1.3).Footnote
10
$\in $
-induction (which implements the vague Principle 2 in Section 1.3).Footnote
10
-
-
6. Our main method of extending a given predicative set theory T to a stronger predicative set theory
 $\mathbf {T}^\star $
is by adding a new symbol to the signature of T, together with an axiom that defines it. (In addition, we include of course in
$\mathbf {T}^\star $
is by adding a new symbol to the signature of T, together with an axiom that defines it. (In addition, we include of course in
 $\mathbf {T}^\star $
all the instances in the extended language of the axiom schemas of T.) Such an extension is done by applying one of the syntactic methods that
$\mathbf {T}^\star $
all the instances in the extended language of the axiom schemas of T.) Such an extension is done by applying one of the syntactic methods that
 $\mathbf {PW}$
provides for this purpose.
$\mathbf {PW}$
provides for this purpose. -
7. As usual, extending T by an operation symbol is allowed only if T proves some corresponding existence and uniqueness conditions. Still, the extension is usually not conservative.
-
8. Adding an n-ary predicate symbol P is allowed only if its defining axiom implies its absoluteness. Similarly, adding an n-ary operation symbol F is allowed only if its defining axiom implies that the formula
 $y=F(x_1,\ldots ,x_n)$
is invariant with respect to y in case
$y=F(x_1,\ldots ,x_n)$
is invariant with respect to y in case
 $y,x_1,\ldots ,x_n$
are distinct.
$y,x_1,\ldots ,x_n$
are distinct.
Note 1.6. In designing
![]() $\mathbf {PW}$
we have adopted two additional principles:
$\mathbf {PW}$
we have adopted two additional principles:
-
• Platonists should be able to accept any theory in our framework. In particular, every such theory is actually a subsystem of
 $\mathbf {ZF}-(P)$
(ZF without the powerset axiom). This principle immediately rules out, e.g., Axiom VIII (Enumerability) of
$\mathbf {ZF}-(P)$
(ZF without the powerset axiom). This principle immediately rules out, e.g., Axiom VIII (Enumerability) of
 $\mathbf {PS_1E}$
from [Reference Feferman, Scott and Jech18] and the Axiom of Countability of
$\mathbf {PS_1E}$
from [Reference Feferman, Scott and Jech18] and the Axiom of Countability of
 $\mathbf {ATR_0^{Set}}$
from [Reference Simpson46] (which says that every set is countable).Footnote
11
$\mathbf {ATR_0^{Set}}$
from [Reference Simpson46] (which says that every set is countable).Footnote
11
-
• Every rule or axiom of
 $\mathbf {PW}$
is a very close counterpart of some rule or axiom that was used by Feferman in one of his predicative (or locally predicative) systems. Hence
$\mathbf {PW}$
is a very close counterpart of some rule or axiom that was used by Feferman in one of his predicative (or locally predicative) systems. Hence
 $\mathbf {PW}$
should be accepted as predicative by anyone who accepts those systems of Feferman’s as predicative.
$\mathbf {PW}$
should be accepted as predicative by anyone who accepts those systems of Feferman’s as predicative.
Note 1.7. Among the axioms of ZFC,
![]() $\mathbf {PW}$
completely rejects the axiom of powerset and the axiom of choice, and it restricts the axiom schema of separation to the case in which the separating condition is absolute. It also accepts only special cases of the axiom schema of replacement. In our opinion, these are properties that should be shared by any predicative set theory.
$\mathbf {PW}$
completely rejects the axiom of powerset and the axiom of choice, and it restricts the axiom schema of separation to the case in which the separating condition is absolute. It also accepts only special cases of the axiom schema of replacement. In our opinion, these are properties that should be shared by any predicative set theory.
Note 1.8. At least in my opinion,
![]() $\mathbf {PW}$
is simpler and easier to work in than any of Feferman’s systems (see Section 4.4). Moreover, we believe that as long as we confine ourselves to
$\mathbf {PW}$
is simpler and easier to work in than any of Feferman’s systems (see Section 4.4). Moreover, we believe that as long as we confine ourselves to
![]() $\mathbf {ZF}-(P)$
(i.e., neither the powerset axiom nor the axiom of choice is allowed to be used), working in
$\mathbf {ZF}-(P)$
(i.e., neither the powerset axiom nor the axiom of choice is allowed to be used), working in
![]() $\mathbf {PW}$
exactly reflects the way work in set theory is done in reality. In particular, one can use abstraction terms as well introduce new operation and predicate symbols in the usual way. Only when there is a worry whether what is done is predicatively justified, a need arises to check whether certain syntactic conditions are satisfied. In most cases this only involves checking whether a certain formula is bounded or is a
$\mathbf {PW}$
exactly reflects the way work in set theory is done in reality. In particular, one can use abstraction terms as well introduce new operation and predicate symbols in the usual way. Only when there is a worry whether what is done is predicatively justified, a need arises to check whether certain syntactic conditions are satisfied. In most cases this only involves checking whether a certain formula is bounded or is a
![]() $\Sigma $
-formula in the usual sense of this concept (see Note 4.7). However, there is one important case (the comprehension schema) in which one should check for some formula
$\Sigma $
-formula in the usual sense of this concept (see Note 4.7). However, there is one important case (the comprehension schema) in which one should check for some formula
![]() $\varphi $
whether
$\varphi $
whether
![]() $\varphi \succ \{x_1,\ldots ,x_n\}$
or not (where
$\varphi \succ \{x_1,\ldots ,x_n\}$
or not (where
![]() $x_1,\ldots ,x_n$
are variables). This is also rather easy once one gets used to the syntactic definition of
$x_1,\ldots ,x_n$
are variables). This is also rather easy once one gets used to the syntactic definition of
![]() $\succ $
, since that definition closely follows the logical structure of
$\succ $
, since that definition closely follows the logical structure of
![]() $\varphi $
. In fact, what is involved is just a short mechanical check, which is usually much easier than proving that the existence of a certain set logically follows from the standard comprehension axioms of
$\varphi $
. In fact, what is involved is just a short mechanical check, which is usually much easier than proving that the existence of a certain set logically follows from the standard comprehension axioms of
![]() $\mathbf {ZF}-(P)$
(or full
$\mathbf {ZF}-(P)$
(or full
![]() $\mathbf {ZF}$
).
$\mathbf {ZF}$
).
1.5 The structure of the paper
Section 2 explains our notations and terminology. Section 3 establishes the predicativity of the set of natural numbers, using a rather weak subsystem of
![]() $\mathbf {PW}$
.
$\mathbf {PW}$
.
![]() $\mathbf {PW}$
itself is precisely defined, justified, and compared with Feferman’s Systems in Section 4. Section 5 includes important examples of the power of
$\mathbf {PW}$
itself is precisely defined, justified, and compared with Feferman’s Systems in Section 4. Section 5 includes important examples of the power of
![]() $\mathbf {PW}$
. Section 6 develops in
$\mathbf {PW}$
. Section 6 develops in
![]() $\mathbf {PW}$
the fundamentals of the theory of von Neumann ordinals. Section 7 includes the main results of this paper: that
$\mathbf {PW}$
the fundamentals of the theory of von Neumann ordinals. Section 7 includes the main results of this paper: that
![]() $\mathbf {PW}$
provides terms which define
$\mathbf {PW}$
provides terms which define
![]() $\Gamma _0$
and much bigger ordinals, and that it can prove the main properties of those ordinals. We conclude in Section 8 with some remarks and directions for further research.
$\Gamma _0$
and much bigger ordinals, and that it can prove the main properties of those ordinals. We conclude in Section 8 with some remarks and directions for further research.
2 Terminology and notations
2.1 The difference between operations and functions
In standard textbooks on first-order theory, it is common to refer to the symbols in a signature of a first-order language as ‘relation symbols’ and ‘function symbols’. We cannot use this terminology here, since we reserve the words ‘relation’ and ‘function’ to their official meaning in set theory, that is, to sets of pairs satisfying certain conditions. Instead, we use the name ‘predicate’ for any “relation” that is not a set (like the predicates
![]() $\in $
or
$\in $
or
![]() $=$
), and we use the name ‘operation’ for any “function” that is not a set (like the operation of union on sets or the operation of addition on ordinals).Footnote
12
Accordingly, the symbols of a first-order signature are divided in this paper into predicate symbols, operation symbols, and constants. The latter may actually be viewed as operations with arity 0, except that they should always be interpreted as sets.
$=$
), and we use the name ‘operation’ for any “function” that is not a set (like the operation of union on sets or the operation of addition on ordinals).Footnote
12
Accordingly, the symbols of a first-order signature are divided in this paper into predicate symbols, operation symbols, and constants. The latter may actually be viewed as operations with arity 0, except that they should always be interpreted as sets.
2.2 Notations
We assume that every first-order language for a set theory has infinitely many variables for sets, officially taken here to be
![]() $v_0,v_1,\ldots $
. We use letters (small or capital) from the end of the Latin alphabet to vary over these variables, and letters from the beginning of that alphabet as general variables for sets in the metalanguage. As usual,
$v_0,v_1,\ldots $
. We use letters (small or capital) from the end of the Latin alphabet to vary over these variables, and letters from the beginning of that alphabet as general variables for sets in the metalanguage. As usual,
![]() $i,j,k,l,m,n$
are used as special variables for natural numbers (in both the metalanguage and the formal language). t and s serve as variables (in the metalanguage) for terms, and
$i,j,k,l,m,n$
are used as special variables for natural numbers (in both the metalanguage and the formal language). t and s serve as variables (in the metalanguage) for terms, and
![]() $\varphi ,\psi ,\theta $
(and sometimes also A and B) as variables for formulas. In all cases the variables may be decorated with subscripts or superscripts. We denote by
$\varphi ,\psi ,\theta $
(and sometimes also A and B) as variables for formulas. In all cases the variables may be decorated with subscripts or superscripts. We denote by
![]() $Fv(\varphi )$
(
$Fv(\varphi )$
(
![]() $Fv(t)$
) the set of free variables of
$Fv(t)$
) the set of free variables of
![]() $\varphi $
(of t). When we denote a formula by
$\varphi $
(of t). When we denote a formula by
![]() $\varphi (x_1,\ldots ,x_n)$
it means that
$\varphi (x_1,\ldots ,x_n)$
it means that
![]() $\{x_1,\ldots ,x_n\}\subseteq Fv(\varphi )$
. On the other hand, when we write
$\{x_1,\ldots ,x_n\}\subseteq Fv(\varphi )$
. On the other hand, when we write
![]() $\varphi (\vec {y},x)$
it means that
$\varphi (\vec {y},x)$
it means that
![]() $\vec {y}=\langle y_1,\ldots ,y_n \rangle $
for some n (whose identity may be obtained from the context or it does not matter); the variables
$\vec {y}=\langle y_1,\ldots ,y_n \rangle $
for some n (whose identity may be obtained from the context or it does not matter); the variables
![]() $x,y_1,\ldots ,y_n$
are all distinct from each other; and
$x,y_1,\ldots ,y_n$
are all distinct from each other; and
![]() $Fv(\varphi )=\{x,y_1,\ldots ,y_n\}$
.
$Fv(\varphi )=\{x,y_1,\ldots ,y_n\}$
.
The substitution of a term t for a free variable y in a formula
![]() $\varphi $
(a term s) is denoted by
$\varphi $
(a term s) is denoted by
![]() $\varphi \{t/y\}$
(
$\varphi \{t/y\}$
(
![]() $s\{t/y\}$
). However, when we denote a formula by
$s\{t/y\}$
). However, when we denote a formula by
![]() $\varphi (y)$
(
$\varphi (y)$
(
![]() $\varphi (x,y)$
,
$\varphi (x,y)$
,
![]() $\varphi (\vec {x},y)$
) we might simply write
$\varphi (\vec {x},y)$
) we might simply write
![]() $\varphi (t)$
(
$\varphi (t)$
(
![]() $\varphi (x,t)$
,
$\varphi (x,t)$
,
![]() $\varphi (\vec {x},t)$
) instead.
$\varphi (\vec {x},t)$
) instead.
Given a first-order signature
![]() $\sigma $
, we take a structure for
$\sigma $
, we take a structure for
![]() $\sigma $
to be a pair
$\sigma $
to be a pair
![]() $\mathcal {M}=\langle \mathcal {D},I \rangle $
, where
$\mathcal {M}=\langle \mathcal {D},I \rangle $
, where
![]() $\mathcal {D}\neq \emptyset $
is the domain of
$\mathcal {D}\neq \emptyset $
is the domain of
![]() $\mathcal {M}$
and I is its interpretation function. If r is one of the symbols in
$\mathcal {M}$
and I is its interpretation function. If r is one of the symbols in
![]() $\sigma $
we shall usually write
$\sigma $
we shall usually write
![]() $r^I$
instead of
$r^I$
instead of
![]() $I(r)$
. If
$I(r)$
. If
![]() $\nu $
is an assignment of elements of
$\nu $
is an assignment of elements of
![]() $\mathcal {D}$
to variables of the language,
$\mathcal {D}$
to variables of the language,
![]() $x_1,\ldots ,x_n$
are n distinct variables, and
$x_1,\ldots ,x_n$
are n distinct variables, and
![]() $\vec {a}\in \mathcal {D}^n$
, we denote by
$\vec {a}\in \mathcal {D}^n$
, we denote by
![]() $\nu \{\vec {x}:=\vec {a}\}$
the assignment which is obtained from
$\nu \{\vec {x}:=\vec {a}\}$
the assignment which is obtained from
![]() $\nu $
by assigning
$\nu $
by assigning
![]() $a_i$
to
$a_i$
to
![]() $x_i$
(
$x_i$
(
![]() $i=1,\ldots ,n$
). We denote by
$i=1,\ldots ,n$
). We denote by
![]() $\nu _{\mathcal {M}}[t]$
the element of
$\nu _{\mathcal {M}}[t]$
the element of
![]() $\mathcal {D}$
that
$\mathcal {D}$
that
![]() $\nu $
assigns according to I to the term t of
$\nu $
assigns according to I to the term t of
![]() $\sigma $
. Similarly, if f is an operation symbol of
$\sigma $
. Similarly, if f is an operation symbol of
![]() $\sigma $
then we use in the metalanguage square brackets to denote applications of
$\sigma $
then we use in the metalanguage square brackets to denote applications of
![]() $f^I$
to arguments in
$f^I$
to arguments in
![]() $\mathcal {D}$
. Thus, if f is n-ary, and
$\mathcal {D}$
. Thus, if f is n-ary, and
![]() $\nu $
is an assignment in
$\nu $
is an assignment in
![]() $\mathcal {D}$
, then
$\mathcal {D}$
, then
![]() $\nu _{\mathcal {M}}[f(t_1,\ldots ,t_n)]=f^I[\nu _{\mathcal {M}}[t_1],\ldots ,\nu _{\mathcal {M}}[t_n]]$
. We write
$\nu _{\mathcal {M}}[f(t_1,\ldots ,t_n)]=f^I[\nu _{\mathcal {M}}[t_1],\ldots ,\nu _{\mathcal {M}}[t_n]]$
. We write
![]() $\mathcal {M},\nu \models \varphi $
in case
$\mathcal {M},\nu \models \varphi $
in case
![]() $\nu $
satisfies in
$\nu $
satisfies in
![]() $\mathcal {M}$
the formula
$\mathcal {M}$
the formula
![]() $\varphi $
of
$\varphi $
of
![]() $\sigma $
. If
$\sigma $
. If
![]() $Fv(\varphi )=\{x_1,\ldots ,x_n\}$
, and
$Fv(\varphi )=\{x_1,\ldots ,x_n\}$
, and
![]() $\nu [x_i]=a_i$
(
$\nu [x_i]=a_i$
(
![]() $i=1,\ldots ,n$
) then we might write instead
$i=1,\ldots ,n$
) then we might write instead
![]() $\mathcal {M}\models \varphi (a_1,\ldots ,a_n)$
.
$\mathcal {M}\models \varphi (a_1,\ldots ,a_n)$
.
Finally, when we refer in the metalanguage to the collection of things that satisfy a certain condition C we shall denote it by
![]() $[x\mid C(x)]$
, reserving the notation
$[x\mid C(x)]$
, reserving the notation
![]() $\{x\!\mid \!\varphi (x)\}$
for being used in our formal system. Moreover, in case there is a danger of confusion, we shall use ‘:’ in the metalanguage instead of ‘
$\{x\!\mid \!\varphi (x)\}$
for being used in our formal system. Moreover, in case there is a danger of confusion, we shall use ‘:’ in the metalanguage instead of ‘
![]() $\in $
’. (Recall that the latter is a basic symbol of the language of our system.)
$\in $
’. (Recall that the latter is a basic symbol of the language of our system.)
3 The predicativity of the natural numbers
Recall that all of our systems are based on classical first-order logic with identity.
Our system
![]() $\mathbf {PW}$
includes a constant
$\mathbf {PW}$
includes a constant
![]() $\omega $
for the natural numbers. Before presenting
$\omega $
for the natural numbers. Before presenting
![]() $\mathbf {PW}$
in the next section, we should justify this inclusion on the basis of the invariance criterion. We do that by:
$\mathbf {PW}$
in the next section, we should justify this inclusion on the basis of the invariance criterion. We do that by:
-
1. Providing a bounded formula
 $N(x)$
in the language of set theory that defines when x is a natural number (i.e., a finite von Neumann ordinal).
$N(x)$
in the language of set theory that defines when x is a natural number (i.e., a finite von Neumann ordinal). -
2. Present a basic predicative set theory
 $\mathbf {VBS}$
, in which one can show that
$\mathbf {VBS}$
, in which one can show that
 $N(x)$
is adequate for the task. This is done by proving in it all the properties that one expects from a formula that defines the natural numbers.
$N(x)$
is adequate for the task. This is done by proving in it all the properties that one expects from a formula that defines the natural numbers. -
3. Give an intuitive proof in the metalanguage that the formula
 $N(x)$
is invariant, and so it may be used for defining a new set.
$N(x)$
is invariant, and so it may be used for defining a new set.
We start by presenting
![]() $\mathbf {VBS}$
.Footnote
13
The axioms of this system include the Extensionality axiom [Ext] and the
$\mathbf {VBS}$
.Footnote
13
The axioms of this system include the Extensionality axiom [Ext] and the
![]() $\in $
-induction axiom schema [
$\in $
-induction axiom schema [
![]() $\in $
-ind] from Section 4.1.6, as well as the following four elementary instances of the general predicative comprehension scheme:
$\in $
-ind] from Section 4.1.6, as well as the following four elementary instances of the general predicative comprehension scheme:
-
1. Empty Set ([Em]):
 $$ \begin{align*}\exists Z\forall x(x\in Z\leftrightarrow x\neq x).\end{align*} $$
$$ \begin{align*}\exists Z\forall x(x\in Z\leftrightarrow x\neq x).\end{align*} $$
-
2. Pairing ([Pa]):
 $$ \begin{align*}\forall x\forall y\forall\exists Z\forall w(w\in Z\leftrightarrow w=x\vee w=y).\end{align*} $$
$$ \begin{align*}\forall x\forall y\forall\exists Z\forall w(w\in Z\leftrightarrow w=x\vee w=y).\end{align*} $$
-
3. Union ([U]):
 $$ \begin{align*}\forall x\exists Z\forall w(w\in Z\leftrightarrow\exists y(y\in x\wedge w\in y)).\end{align*} $$
$$ \begin{align*}\forall x\exists Z\forall w(w\in Z\leftrightarrow\exists y(y\in x\wedge w\in y)).\end{align*} $$
-
4. Difference ([D]):
 $$ \begin{align*}\forall x\forall y\exists Z \forall w(w\in Z\leftrightarrow w\in x\wedge w\not\in y).\end{align*} $$
$$ \begin{align*}\forall x\forall y\exists Z \forall w(w\in Z\leftrightarrow w\in x\wedge w\not\in y).\end{align*} $$
Note 3.1. It is easy to see that the structure
![]() $\langle \mathsf {HF},\in \rangle $
, where HF (which is identical to
$\langle \mathsf {HF},\in \rangle $
, where HF (which is identical to
![]() $V_{\omega }$
) is the set of the hereditarily finite sets, forms the minimal model of
$V_{\omega }$
) is the set of the hereditarily finite sets, forms the minimal model of
![]() $\mathbf {VBS}$
. Moreover,
$\mathbf {VBS}$
. Moreover,
![]() $\langle V_\alpha ,\in \rangle $
is a model of
$\langle V_\alpha ,\in \rangle $
is a model of
![]() $\mathbf {VBS}$
whenever
$\mathbf {VBS}$
whenever
![]() $\alpha $
is a limit ordinal.Footnote
14
$\alpha $
is a limit ordinal.Footnote
14
In order to present the formula
![]() $N(x)$
it is convenient (though not really necessary) to use the usual procedure of extension by definitions, and develop
$N(x)$
it is convenient (though not really necessary) to use the usual procedure of extension by definitions, and develop
![]() $\mathbf {VBS}$
in an enriched language in which the four axioms above are replaced by:Footnote
15
$\mathbf {VBS}$
in an enriched language in which the four axioms above are replaced by:Footnote
15
-
1. [Em]:
 $\forall x(x\not \in \emptyset ).$
$\forall x(x\not \in \emptyset ).$
-
2. [Pa]:
 $\forall x\forall y\forall w(w\in \{x,y\}\leftrightarrow w=x\vee w=y).$
$\forall x\forall y\forall w(w\in \{x,y\}\leftrightarrow w=x\vee w=y).$
-
3. [U]:
 $\forall x\forall w(w\in \bigcup x\leftrightarrow \exists y(y \in x\wedge w\in y)).$
$\forall x\forall w(w\in \bigcup x\leftrightarrow \exists y(y \in x\wedge w\in y)).$
-
4. [D]:
 $\forall x\forall y\forall w(w\in x-y\leftrightarrow w\in x\wedge w\not \in y).$
$\forall x\forall y\forall w(w\in x-y\leftrightarrow w\in x\wedge w\not \in y).$
Note 3.2. In general, one should be careful when applying the extension by definitions procedure to theories with axioms schemas, since the extension of such a schema to the expanded language involves the addition of infinitely many new axioms besides those that are allowed by the procedure. This is not a problem in cases like we have here, where every axiom schema is pure in the sense that no constraint is imposed on the formulas to which it may be applied. Therefore we may assume that every instance of
![]() $[{\in}{-}ind]$
in the expanded language is an axiom of
$[{\in}{-}ind]$
in the expanded language is an axiom of
![]() $\mathbf {VBS}$
. However, one should be cautious about the issue of being conservative when the procedure is applied in more complicated cases, like in case we have
$\mathbf {VBS}$
. However, one should be cautious about the issue of being conservative when the procedure is applied in more complicated cases, like in case we have
![]() $[{\in}{-}ind]$
restricted to some class of formulas (e.g., bounded formulas).
$[{\in}{-}ind]$
restricted to some class of formulas (e.g., bounded formulas).
Proposition 3.3. For every
![]() $n\geq 0$
,
$n\geq 0$
,
Proof We do the case
![]() $n=2$
(which trivially implies the cases
$n=2$
(which trivially implies the cases
![]() $n=0$
and
$n=0$
and
![]() $n=1$
). The proof for any other n is similar.
$n=1$
). The proof for any other n is similar.
Given
![]() $x_0$
, to show that
$x_0$
, to show that
![]() $\forall x_1\in x_0\forall x_2\in x_1.x_0\not \in x_2$
, we may assume (using
$\forall x_1\in x_0\forall x_2\in x_1.x_0\not \in x_2$
, we may assume (using
![]() $[{\in}{-}ind]$
) that
$[{\in}{-}ind]$
) that
![]() $(\star )\mbox {\ \ \ } \forall y_0 \in x_0 \forall y_1\in y_0\forall y_2\in y_1.y_0\not \in y_2$
. Suppose now that there are
$(\star )\mbox {\ \ \ } \forall y_0 \in x_0 \forall y_1\in y_0\forall y_2\in y_1.y_0\not \in y_2$
. Suppose now that there are
![]() $x_1$
and
$x_1$
and
![]() $x_2$
such that:
$x_2$
such that:
![]() $x_1\in x_0\wedge x_2\in x_1\wedge x_0\in x_2$
Since
$x_1\in x_0\wedge x_2\in x_1\wedge x_0\in x_2$
Since
![]() $x_1\in x_0$
, we may apply
$x_1\in x_0$
, we may apply
![]() $(\star )$
with
$(\star )$
with
![]() $y_0=x_1$
,
$y_0=x_1$
,
![]() $y_1=x_2$
, and
$y_1=x_2$
, and
![]() $y_2=x_0$
, to get that
$y_2=x_0$
, to get that
![]() $x_1\not \in x_0$
, which is a contradiction. So no such
$x_1\not \in x_0$
, which is a contradiction. So no such
![]() $x_1$
and
$x_1$
and
![]() $x_2$
exist.
$x_2$
exist.
We are ready to introduce our definition of the notion of a natural number:
Definition 3.4.
-
1.
 $S(x):=x\cup \{x\}$
(where
$S(x):=x\cup \{x\}$
(where
 $\{x\}=\{x,x\}$
).
$\{x\}=\{x,x\}$
). -
2.
 $N(x):=\forall y\in S(x)( y=\emptyset \vee \exists z\in x. y=S(z)).$
$N(x):=\forall y\in S(x)( y=\emptyset \vee \exists z\in x. y=S(z)).$
Note 3.5. Officially,
![]() $N(x)$
is the following formula:
$N(x)$
is the following formula:
Proposition 3.6. Let
![]() $0:=\emptyset $
. The following are provable in
$0:=\emptyset $
. The following are provable in
![]() $\mathbf {VBS}$
:
$\mathbf {VBS}$
:
-
1.
 $N(0)$
.
$N(0)$
. -
2.
 $\forall x(N(x)\leftrightarrow N(S(x)))$
.
$\forall x(N(x)\leftrightarrow N(S(x)))$
. -
3.
 $S(x)\neq 0.$
$S(x)\neq 0.$
-
4.
 $S(x)=S(y) \to x=y.$
$S(x)=S(y) \to x=y.$
Proof Points 1 and 3 are trivial. Point 4 easily follows from Proposition 3.3. We show point 2.
-
• Suppose that
 $N(x)$
. We show that
$N(x)$
. We show that
 $N(S(x))$
, i.e., that So let
$N(S(x))$
, i.e., that So let $$ \begin{align*}\forall y\in S(S(x))( y=0\vee\exists z\in S(x). y=S(z)).\end{align*} $$
$$ \begin{align*}\forall y\in S(S(x))( y=0\vee\exists z\in S(x). y=S(z)).\end{align*} $$
 $y\in S(S(x))$
. We show that
$y\in S(S(x))$
. We show that
 $y=0\vee \exists z\in S(x). y=S(z)$
. Since we assume
$y=0\vee \exists z\in S(x). y=S(z)$
. Since we assume
 $N(x)$
, this is obvious in case
$N(x)$
, this is obvious in case
 $y\in S(x)$
, because every
$y\in S(x)$
, because every
 $z\in x$
is also in
$z\in x$
is also in
 $S(x)$
. There remains the case
$S(x)$
. There remains the case
 $y=S(x)$
, but this case is trivial, since
$y=S(x)$
, but this case is trivial, since
 $x\in S(x)$
(and so x is an element z in
$x\in S(x)$
(and so x is an element z in
 $S(x)$
such that
$S(x)$
such that
 $y=S(z)$
).
$y=S(z)$
).
-
• Suppose that
 $N(S(x))$
, i.e., We show that
$N(S(x))$
, i.e., We show that $$ \begin{align*}\forall y\in S(S(x))( y=0\vee\exists z\in S(x). y=S(z)).\end{align*} $$
$$ \begin{align*}\forall y\in S(S(x))( y=0\vee\exists z\in S(x). y=S(z)).\end{align*} $$
 $N(x)$
. So let
$N(x)$
. So let
 $y\in S(x)$
. We show that
$y\in S(x)$
. We show that
 $y=0\vee \exists z\in x. y=S(z)$
. Suppose that the first disjunct fails, i.e.,
$y=0\vee \exists z\in x. y=S(z)$
. Suppose that the first disjunct fails, i.e.,
 $y\neq 0$
. Since
$y\neq 0$
. Since
 $S(x)\subseteq S(S(x))$
, our assumption implies that there is
$S(x)\subseteq S(S(x))$
, our assumption implies that there is
 $z\in S(x)$
such that
$z\in S(x)$
such that
 $y=S(z)$
. It is impossible that
$y=S(z)$
. It is impossible that
 $z=x$
, since in this case we would get that
$z=x$
, since in this case we would get that
 $S(x)\in S(x)$
. Hence
$S(x)\in S(x)$
. Hence
 $z\in x$
, and we are done.
$z\in x$
, and we are done.
Proposition 3.7.
![]() $\vdash _{\mathbf {VBS}}\varphi \{0/x\}\wedge \forall x(\varphi \to \varphi \{S(x)/x\})\to \forall x(N(x)\to \varphi ).$
$\vdash _{\mathbf {VBS}}\varphi \{0/x\}\wedge \forall x(\varphi \to \varphi \{S(x)/x\})\to \forall x(N(x)\to \varphi ).$
Proof Assume
![]() $\mathrm {(I)}\ \varphi \{0/x\}\wedge \forall x(\varphi \to \varphi \{S(x)/x\})$
. To show
$\mathrm {(I)}\ \varphi \{0/x\}\wedge \forall x(\varphi \to \varphi \{S(x)/x\})$
. To show
![]() $\forall x(N(x)\to \varphi )$
, it suffices by
$\forall x(N(x)\to \varphi )$
, it suffices by
![]() $[{\in}{-}ind]$
to show that
$[{\in}{-}ind]$
to show that
![]() $\forall x(\forall y\in x(N(y)\to \varphi \{y/x\})\to (N(x)\to \varphi ))$
. So assume that
$\forall x(\forall y\in x(N(y)\to \varphi \{y/x\})\to (N(x)\to \varphi ))$
. So assume that
![]() $\mathrm {(II)}\ \forall y\in x(N(y)\to \varphi \{y/x\})$
and
$\mathrm {(II)}\ \forall y\in x(N(y)\to \varphi \{y/x\})$
and
![]() $\mathrm {(III)}\ N(x)$
. We show
$\mathrm {(III)}\ N(x)$
. We show
![]() $\varphi $
. If
$\varphi $
. If
![]() $x=0$
then this is implied by (I). If not, then it follows from (III) that there is
$x=0$
then this is implied by (I). If not, then it follows from (III) that there is
![]() $z\in x$
such that
$z\in x$
such that
![]() $x=S(z)$
. Hence (II) entails that
$x=S(z)$
. Hence (II) entails that
![]() $N(z)\to \varphi \{z/x\}$
. But
$N(z)\to \varphi \{z/x\}$
. But
![]() $N(z)$
follows from (III) by the second item of Proposition 3.6. Therefore
$N(z)$
follows from (III) by the second item of Proposition 3.6. Therefore
![]() $\varphi \{z/x\}$
. From this
$\varphi \{z/x\}$
. From this
![]() $\varphi $
(which is equivalent to
$\varphi $
(which is equivalent to
![]() $\varphi \{S(z)/x\}$
) follows by (I).
$\varphi \{S(z)/x\}$
) follows by (I).
Proposition 3.8. Let
![]() $<:=\in $
. The following are provable in
$<:=\in $
. The following are provable in
![]() $\mathbf {VBS}$
:
$\mathbf {VBS}$
:
-
1.
 $x\not <0.$
$x\not <0.$
-
2.
 $x<S(y) \leftrightarrow x<y\vee x=y.$
$x<S(y) \leftrightarrow x<y\vee x=y.$
-
3.
 $N(x)\wedge y<x\to N(y).$
$N(x)\wedge y<x\to N(y).$
Proof The first two items are trivial. We prove the third by induction on x (i.e., by using Proposition 3.7). So let
![]() $\varphi :=\forall y(N(x)\wedge y<x\to N(y))$
. Obviously,
$\varphi :=\forall y(N(x)\wedge y<x\to N(y))$
. Obviously,
![]() $\vdash _{\mathbf {VBS}}\varphi \{0/x\}$
. We show that
$\vdash _{\mathbf {VBS}}\varphi \{0/x\}$
. We show that
![]() $\vdash _{\mathbf {VBS}}\forall x(\varphi \to \varphi \{S(x)/x\})$
. So assume
$\vdash _{\mathbf {VBS}}\forall x(\varphi \to \varphi \{S(x)/x\})$
. So assume
![]() $\varphi (x)$
and that
$\varphi (x)$
and that
![]() $N(S(x))$
and
$N(S(x))$
and
![]() $y<S(x)$
. By Proposition 3.6, the first assumption implies that
$y<S(x)$
. By Proposition 3.6, the first assumption implies that
![]() $N(x)$
. Hence
$N(x)$
. Hence
![]() $y=x$
implies that
$y=x$
implies that
![]() $N(y)$
. Otherwise
$N(y)$
. Otherwise
![]() $y<x$
, and so the induction hypothesis implies that
$y<x$
, and so the induction hypothesis implies that
![]() $N(y)$
.
$N(y)$
.
Finally we show that
![]() $N(x)$
(intuitively) defines an invariant collection. Since this is an intuitive theorem in the meta-language, the proof is intuitive too. Still, it employs only predicatively acceptable principles.
$N(x)$
(intuitively) defines an invariant collection. Since this is an intuitive theorem in the meta-language, the proof is intuitive too. Still, it employs only predicatively acceptable principles.
Proposition 3.9. Let
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
be transitive models of VBS (in the usual sense of set theory) such that
$\mathcal {M}_2$
be transitive models of VBS (in the usual sense of set theory) such that
![]() $\mathcal {M}_1\subseteq \mathcal {M}_2$
. Then:
$\mathcal {M}_1\subseteq \mathcal {M}_2$
. Then:
Proof The fact that
![]() $N(x)$
is bounded (and so absolute) implies that
$N(x)$
is bounded (and so absolute) implies that
![]() $\omega _1\subseteq \omega _2$
. For the converse, we show that
$\omega _1\subseteq \omega _2$
. For the converse, we show that
![]() $\forall a\in \mathcal {M}_2((\mathcal {M}_2\models N(a))\to (a\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(a)))$
. So let
$\forall a\in \mathcal {M}_2((\mathcal {M}_2\models N(a))\to (a\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(a)))$
. So let
![]() $a\in \mathcal {M}_2$
, and assume that
$a\in \mathcal {M}_2$
, and assume that
![]() $\mathcal {M}_2\models N(a)$
. By
$\mathcal {M}_2\models N(a)$
. By
![]() $[{\in}{-}ind]$
we may assume also that
$[{\in}{-}ind]$
we may assume also that
![]() $\forall b\in a((\mathcal {M}_2\models N(b))\to (b\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(b)))$
. Since
$\forall b\in a((\mathcal {M}_2\models N(b))\to (b\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(b)))$
. Since
![]() $\mathcal {M}_2\models N(a)$
, either
$\mathcal {M}_2\models N(a)$
, either
![]() $a=\emptyset $
, or there exists
$a=\emptyset $
, or there exists
![]() $b\in a$
such that
$b\in a$
such that
![]() $\mathcal {M}_2\models a=S(b)$
. In the first case
$\mathcal {M}_2\models a=S(b)$
. In the first case
![]() $a\in \mathcal {M}_1$
holds trivially. So assume the second case. Then item 2 of Proposition 3.6 implies that
$a\in \mathcal {M}_1$
holds trivially. So assume the second case. Then item 2 of Proposition 3.6 implies that
![]() $\mathcal {M}_2\models N(b)$
. Hence the induction hypothesis implies that
$\mathcal {M}_2\models N(b)$
. Hence the induction hypothesis implies that
![]() $b\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(b)$
. Again by Proposition 3.6, this entails that
$b\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(b)$
. Again by Proposition 3.6, this entails that
![]() $S(b)\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(S(b))$
. Hence
$S(b)\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(S(b))$
. Hence
![]() $a\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(a)$
.
$a\in \mathcal {M}_1\wedge \mathcal {M}_1\models N(a)$
.
4 The system
 $\mathbf {PW}$
$\mathbf {PW}$
4.1 A description of the system
The language of the system
![]() $\mathbf {PW}$
is an one-sorted first-order language with equality. As in Section 2, we take its variables to be
$\mathbf {PW}$
is an one-sorted first-order language with equality. As in Section 2, we take its variables to be
![]() $v_0,v_1,\ldots $
, and use letters (both small and capital) from the end of the Latin alphabet to vary over them. All other components of the language (predicate and operation symbols, terms, formulas, the invariance relation
$v_0,v_1,\ldots $
, and use letters (both small and capital) from the end of the Latin alphabet to vary over them. All other components of the language (predicate and operation symbols, terms, formulas, the invariance relation
![]() $\succ $
and the
$\succ $
and the
![]() $\Sigma $
-formulas) are simultaneously generated as described in Sections 4.1.1–4.1.5. The axioms and rules of
$\Sigma $
-formulas) are simultaneously generated as described in Sections 4.1.1–4.1.5. The axioms and rules of
![]() $\mathbf {PW}$
are presented in Sections 4.1.6 and 4.1.7, respectively. (Note that in the formulation of the last rule [Unif] there is a use of the formula
$\mathbf {PW}$
are presented in Sections 4.1.6 and 4.1.7, respectively. (Note that in the formulation of the last rule [Unif] there is a use of the formula
![]() $Fun$
, the operation
$Fun$
, the operation
![]() $Dom$
, and the term
$Dom$
, and the term
![]() $f(x)$
. They are all introduced in Section 5.1 without using [Unif].
$f(x)$
. They are all introduced in Section 5.1 without using [Unif].
![]() $Fun(f)$
says that f is a function.
$Fun(f)$
says that f is a function.
![]() $Dom(f)$
and
$Dom(f)$
and
![]() $f(x)$
have their usual meanings.)
$f(x)$
have their usual meanings.)
4.1.1 Predicate symbols and operation symbols
-
1.
 $=$
and
$=$
and
 $\in $
are binary predicate symbols.
$\in $
are binary predicate symbols. -
2.
 $\omega $
is a constant (i.e., an 0-ary operation symbol).
$\omega $
is a constant (i.e., an 0-ary operation symbol). -
3. If
 $\varphi \succ \emptyset $
and
$\varphi \succ \emptyset $
and
 $Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
then
$Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
then
 $P_{\varphi }$
is an
$P_{\varphi }$
is an
 $n+1$
predicate symbol.
$n+1$
predicate symbol. -
4. If
 $\varphi $
is
$\varphi $
is
 $\Sigma $
and
$\Sigma $
and
 $Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
then
$Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
then
 $F_{\varphi }$
is an n-ary operation symbol.
$F_{\varphi }$
is an n-ary operation symbol.
4.1.2 Terms
-
1. Every variable is a term.
-
2.
 $F(t_1 ,\ldots \!,\! t_n)$
is a term if F is an n-ary operation, and
$F(t_1 ,\ldots \!,\! t_n)$
is a term if F is an n-ary operation, and
 $t_1 ,\ldots \!,\! t_n$
are terms.
$t_1 ,\ldots \!,\! t_n$
are terms.
4.1.3 Formulas
-
1.
 $P(t_1 ,\ldots \!,\! t_n)$
is a formula if P is an n-ary predicate,
$P(t_1 ,\ldots \!,\! t_n)$
is a formula if P is an n-ary predicate,
 $t_1 ,\ldots \!,\! t_n$
are terms.
$t_1 ,\ldots \!,\! t_n$
are terms. -
2. The formulas are closed under
 $\neg $
,
$\neg $
,
 $\wedge $
,
$\wedge $
,
 $\vee $
, and
$\vee $
, and
 $\to $
.
$\to $
. -
3. If
 $\varphi $
is a formula and x is a variable, then
$\varphi $
is a formula and x is a variable, then
 $\exists x\varphi $
and
$\exists x\varphi $
and
 $\forall x\varphi $
are formulas.
$\forall x\varphi $
are formulas.
4.1.4 The invariance relation
 $\succ $
$\succ $
-
1.
 $t\in s\succ \emptyset $
and
$t\in s\succ \emptyset $
and
 $t=s\succ \emptyset $
.
$t=s\succ \emptyset $
. -
2.
 $P_{\varphi }(t_0 ,\ldots \!,\! t_n)\succ \emptyset $
.
$P_{\varphi }(t_0 ,\ldots \!,\! t_n)\succ \emptyset $
. -
3.
 $\varphi \succ \{x\}$
if
$\varphi \succ \{x\}$
if
 $\varphi \in \{x\neq x,x=t,t=x,x\in t\}$
and
$\varphi \in \{x\neq x,x=t,t=x,x\in t\}$
and
 $x\not \in Fv(t)$
.
$x\not \in Fv(t)$
. -
4.
 $\neg \varphi \succ \emptyset $
if
$\neg \varphi \succ \emptyset $
if
 $\varphi \succ \emptyset $
.
$\varphi \succ \emptyset $
. -
5.
 $\varphi \vee \psi \succ X$
if
$\varphi \vee \psi \succ X$
if
 $\varphi \succ X$
and
$\varphi \succ X$
and
 $\psi \succ X$
.
$\psi \succ X$
. -
6.
 $\varphi \wedge \psi \succ X\cup Y$
if
$\varphi \wedge \psi \succ X\cup Y$
if
 $\varphi \succ X$
,
$\varphi \succ X$
,
 $\psi \succ Y$
and
$\psi \succ Y$
and
 $Y\cap Fv(\varphi )=\emptyset $
.
$Y\cap Fv(\varphi )=\emptyset $
. -
7.
 $\exists y \varphi \succ X-\{y\}$
if
$\exists y \varphi \succ X-\{y\}$
if
 $y\in X$
and
$y\in X$
and
 $\varphi \succ X$
.
$\varphi \succ X$
.
4.1.5
 $\Sigma $
-formulas
$\Sigma $
-formulas
-
1. If
 $\varphi \succ \emptyset $
then
$\varphi \succ \emptyset $
then
 $\varphi $
is
$\varphi $
is
 $\Sigma $
. Such formulas are called absolute.
$\Sigma $
. Such formulas are called absolute. -
2. If
 $\varphi $
and
$\varphi $
and
 $\psi $
are
$\psi $
are
 $\Sigma $
then so are
$\Sigma $
then so are
 $\varphi \vee \psi $
and
$\varphi \vee \psi $
and
 $\varphi \wedge \psi $
.
$\varphi \wedge \psi $
. -
3. If
 $\varphi $
is
$\varphi $
is
 $\Sigma $
then so is
$\Sigma $
then so is
 $\exists x\varphi $
.
$\exists x\varphi $
. -
4. If
 $\varphi \succ \{y_1,\ldots \!,\! y_k\}$
, and
$\varphi \succ \{y_1,\ldots \!,\! y_k\}$
, and
 $\psi $
is
$\psi $
is
 $\Sigma $
, then
$\Sigma $
, then
 $\forall y_1\dots \forall y_k(\varphi \to \psi )$
is
$\forall y_1\dots \forall y_k(\varphi \to \psi )$
is
 $\Sigma $
.
$\Sigma $
.
4.1.6 Axioms
-
1. [Fol]: Every formula which is valid in first-order logic with equality.Footnote 16
-
2. [Ext] (Extensionality):
 $\forall z (z\in x \leftrightarrow z\in y)\to x=y$
.
$\forall z (z\in x \leftrightarrow z\in y)\to x=y$
. -
3. [Comp] (
 $\succ $
-Comprehension):
$\succ $
-Comprehension):
 $\exists !Z\forall x(x\in Z\leftrightarrow \varphi )$
, provided that
$\exists !Z\forall x(x\in Z\leftrightarrow \varphi )$
, provided that
 $\varphi \succ \{x\}$
.Footnote
17
$\varphi \succ \{x\}$
.Footnote
17
-
4. [
 $\in $
-ind] (
$\in $
-ind] (
 $\in $
-induction):
$\in $
-induction):
 $(\forall x(\forall y(y\in x\to \varphi \{y/x\})\to \varphi ))\to \forall x\varphi $
.
$(\forall x(\forall y(y\in x\to \varphi \{y/x\})\to \varphi ))\to \forall x\varphi $
. -
5. [Inf] (Infinity):
 $\forall x(x\in \omega \leftrightarrow N(x))$
, where
$\forall x(x\in \omega \leftrightarrow N(x))$
, where
 $N(x)$
is presented in Note 3.5.
$N(x)$
is presented in Note 3.5. -
6. [PrI]
 $P_{\varphi }(v_0 ,\ldots \!,\! v_{n})\leftrightarrow \varphi $
(provided that
$P_{\varphi }(v_0 ,\ldots \!,\! v_{n})\leftrightarrow \varphi $
(provided that
 $\varphi $
is as in Section 4.1.1).
$\varphi $
is as in Section 4.1.1).
4.1.7 Rules
-
1. [MP]: From
 $\varphi $
and
$\varphi $
and
 $\varphi \to \psi $
infer
$\varphi \to \psi $
infer
 $\psi $
.
$\psi $
. -
2. [Gen]: From
 $\vdash _{\mathbf {PW}}\varphi $
infer
$\vdash _{\mathbf {PW}}\varphi $
infer
 $\vdash _{\mathbf {PW}}\forall x\varphi $
.
$\vdash _{\mathbf {PW}}\forall x\varphi $
. -
3. [OpI] From
 $\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n\exists !v_0\varphi $
infer
$\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n\exists !v_0\varphi $
infer
 $\vdash _{\mathbf {PW}} F_{\varphi }(v_1 ,\ldots \!,\! v_n)=v_0\leftrightarrow \varphi $
(provided that
$\vdash _{\mathbf {PW}} F_{\varphi }(v_1 ,\ldots \!,\! v_n)=v_0\leftrightarrow \varphi $
(provided that
 $\varphi $
is as in Section 4.1.1, i.e.,
$\varphi $
is as in Section 4.1.1, i.e.,
 $\varphi $
is
$\varphi $
is
 $\Sigma $
and
$\Sigma $
and
 $Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
).
$Fv(\varphi )=\{v_0 ,\ldots \!,\! v_{n}\}$
). -
4. [Unif] (Unification Rule):
 $$\begin{align*}\frac {\vdash_{\mathbf{PW}}\forall y_1\forall y_2(\varphi\{y_1/y\}\wedge\varphi\{y_2/y\}\to y_1=y_2)} {\vdash_{\mathbf{PW}}\forall x\in Z\exists y \varphi\to\exists!f(Fun(f)\wedge Dom(f)=Z\wedge \forall x\in Z\varphi\{f(x)/y\})}. \end{align*}$$
$$\begin{align*}\frac {\vdash_{\mathbf{PW}}\forall y_1\forall y_2(\varphi\{y_1/y\}\wedge\varphi\{y_2/y\}\to y_1=y_2)} {\vdash_{\mathbf{PW}}\forall x\in Z\exists y \varphi\to\exists!f(Fun(f)\wedge Dom(f)=Z\wedge \forall x\in Z\varphi\{f(x)/y\})}. \end{align*}$$
Provided
 $\varphi $
is
$\varphi $
is
 $\Sigma $
, x and y are distinct variables in
$\Sigma $
, x and y are distinct variables in
 $Fv(\varphi )$
, and
$Fv(\varphi )$
, and
 $Z\not \in Fv(\varphi )$
.
$Z\not \in Fv(\varphi )$
.
Definition 4.1.
-
1. A proof in
 $\mathbf {PW}$
of a formula
$\mathbf {PW}$
of a formula
 $\varphi $
is a sequence of formulas ending with
$\varphi $
is a sequence of formulas ending with
 $\varphi $
, such that each element of the sequence is either an axiom of
$\varphi $
, such that each element of the sequence is either an axiom of
 $\mathbf {PW}$
or it can be inferred from previous elements of the sequence by one of the four rules of
$\mathbf {PW}$
or it can be inferred from previous elements of the sequence by one of the four rules of
 $\mathbf {PW}$
.
$\mathbf {PW}$
.
 $\varphi $
is a theorem of
$\varphi $
is a theorem of
 $\mathbf {PW}$
if it has a proof in
$\mathbf {PW}$
if it has a proof in
 $\mathbf {PW}$
.
$\mathbf {PW}$
. -
2. A derivation in
 $\mathbf {PW}$
of a formula
$\mathbf {PW}$
of a formula
 $\varphi $
from a set
$\varphi $
from a set
 $\mathbf {T}$
of assumptions is a sequence of formulas ending with
$\mathbf {T}$
of assumptions is a sequence of formulas ending with
 $\varphi $
, such that each element of the sequence is either a theorem of
$\varphi $
, such that each element of the sequence is either a theorem of
 $\mathbf {PW}$
, or an element of
$\mathbf {PW}$
, or an element of
 $\mathbf {T}$
, or it can be inferred from two previous elements of the sequence by [MP].
$\mathbf {T}$
, or it can be inferred from two previous elements of the sequence by [MP].
 $\varphi $
is derivable in
$\varphi $
is derivable in
 $\mathbf {PW}$
from
$\mathbf {PW}$
from
 $\mathbf {T}$
if it has a derivation in
$\mathbf {T}$
if it has a derivation in
 $\mathbf {PW}$
from
$\mathbf {PW}$
from
 $\mathbf {T}$
.
$\mathbf {T}$
.
Note 4.2. It should be emphasized that by Definition 4.1 (as well as by the difference in the way the rules of
![]() $\mathbf {PW}$
are formulated in Section 4.1.7), [MP] is the only rule of derivation of
$\mathbf {PW}$
are formulated in Section 4.1.7), [MP] is the only rule of derivation of
![]() $\mathbf {PW}$
. All the rest are only rules of proof. This means that they can be applied only in assumptions-free derivations (i.e., pure derivations from axioms). It follows that the deduction theorem obtains for
$\mathbf {PW}$
. All the rest are only rules of proof. This means that they can be applied only in assumptions-free derivations (i.e., pure derivations from axioms). It follows that the deduction theorem obtains for
![]() $\mathbf {PW}$
: to show
$\mathbf {PW}$
: to show
![]() $\mathbf {T}\vdash _{\mathbf {PW}}(\varphi \to \psi )$
it suffices to prove that
$\mathbf {T}\vdash _{\mathbf {PW}}(\varphi \to \psi )$
it suffices to prove that
![]() $\mathbf {T},\varphi \vdash _{\mathbf {PW}}\psi $
. However, while using this theorem in order to show that
$\mathbf {T},\varphi \vdash _{\mathbf {PW}}\psi $
. However, while using this theorem in order to show that
![]() $\mathbf {T}\vdash _{\mathbf {PW}}(\varphi \to \psi )$
, one should be careful not to rely on a proof of
$\mathbf {T}\vdash _{\mathbf {PW}}(\varphi \to \psi )$
, one should be careful not to rely on a proof of
![]() $\psi $
from
$\psi $
from
![]() $\mathbf {T}\cup \{\varphi \}$
in which [Gen],[OpI] or [Unif] are applied to a formula which depends on an assumption in
$\mathbf {T}\cup \{\varphi \}$
in which [Gen],[OpI] or [Unif] are applied to a formula which depends on an assumption in
![]() $\mathbf {T}\cup \{\varphi \}$
.Footnote
18
$\mathbf {T}\cup \{\varphi \}$
.Footnote
18
Note 4.3. In the formulation above we have used the quantifier
![]() $\exists !$
in [Comp] and in [Unif]. This was done according to Principle (I) in Section 1.4.2. However, in both cases we can actually use the simpler connective
$\exists !$
in [Comp] and in [Unif]. This was done according to Principle (I) in Section 1.4.2. However, in both cases we can actually use the simpler connective
![]() $\exists $
. In the case of [Comp] this is due to the axiom [Ext], while in the case of [Unif] it follows from the premise of that rule.
$\exists $
. In the case of [Comp] this is due to the axiom [Ext], while in the case of [Unif] it follows from the premise of that rule.
Note 4.4. Like in the system PZF from [Reference Avron and Schindler5], the predicativity of definitions of sets is ensured
![]() $\mathbf {PW}$
by using an appropriate syntactic invariance relation
$\mathbf {PW}$
by using an appropriate syntactic invariance relation
![]() $\succ $
between a formula
$\succ $
between a formula
![]() $\varphi $
and subsets of
$\varphi $
and subsets of
![]() $Fv(\varphi )$
. (The intended meaning of
$Fv(\varphi )$
. (The intended meaning of
![]() $\succ $
was described in item (II) at the beginning of Section 1.4.2.) Relations of this sort have originally been introduced in [Reference Avron and Hendricks3, Reference Avron4] in order to provide a unified theory of constructions and operations as they are used in different branches of mathematics and computer science, including set theory, computability theory, and database theory (see footnote 8). Further important theorems about them can be found in [Reference Avron, Lev and Levi8].Footnote
19
$\succ $
was described in item (II) at the beginning of Section 1.4.2.) Relations of this sort have originally been introduced in [Reference Avron and Hendricks3, Reference Avron4] in order to provide a unified theory of constructions and operations as they are used in different branches of mathematics and computer science, including set theory, computability theory, and database theory (see footnote 8). Further important theorems about them can be found in [Reference Avron, Lev and Levi8].Footnote
19
Note 4.5. It is easy to show by induction that if
![]() $\varphi \succ X$
and
$\varphi \succ X$
and
![]() $Y\subseteq X$
then
$Y\subseteq X$
then
![]() $\varphi \succ Y$
. Therefore we have not included this important condition from [Reference Avron, Lev and Levi8] in our present definition of
$\varphi \succ Y$
. Therefore we have not included this important condition from [Reference Avron, Lev and Levi8] in our present definition of
![]() $\succ $
, but we shall use it freely in what follows. Another important condition which we shall treat as if it included in the definition of
$\succ $
, but we shall use it freely in what follows. Another important condition which we shall treat as if it included in the definition of
![]() $\succ $
is that
$\succ $
is that
![]() $\forall x_1\dots \forall x_n(\varphi \to \psi )\succ \emptyset $
if
$\forall x_1\dots \forall x_n(\varphi \to \psi )\succ \emptyset $
if
![]() $\varphi \succ \{x_1 ,\ldots \!,\! x_n\}$
and
$\varphi \succ \{x_1 ,\ldots \!,\! x_n\}$
and
![]() $\psi \succ \emptyset $
. The reason is that every consequence of this condition can easily be derived without it (because
$\psi \succ \emptyset $
. The reason is that every consequence of this condition can easily be derived without it (because
![]() $\forall x_1\dots \forall x_n(\varphi \to \psi )$
is logically equivalent to
$\forall x_1\dots \forall x_n(\varphi \to \psi )$
is logically equivalent to
![]() $\neg \exists x_1\dots \forall x_n(\varphi \wedge \neg \psi )$
.)
$\neg \exists x_1\dots \forall x_n(\varphi \wedge \neg \psi )$
.)
Note 4.6. The clauses in the definition of
![]() $\Sigma $
-formulas are taken from [Reference Avron4]. This definition is a straightforward generalization of the usual definition of
$\Sigma $
-formulas are taken from [Reference Avron4]. This definition is a straightforward generalization of the usual definition of
![]() $\Sigma $
-formulas. In particular, it includes all the formulas which are called ‘essentially existential HF-formulas’ in [Reference Feferman17]. From Theorem 4.1 of [Reference Feferman17] it follows that every persistent formula is equivalent in
$\Sigma $
-formulas. In particular, it includes all the formulas which are called ‘essentially existential HF-formulas’ in [Reference Feferman17]. From Theorem 4.1 of [Reference Feferman17] it follows that every persistent formula is equivalent in
![]() $\mathbf {PW}$
to a
$\mathbf {PW}$
to a
![]() $\Sigma $
-formula, but we shall not use this fact here.
$\Sigma $
-formula, but we shall not use this fact here.
Note 4.7. By the results of [Reference Avron, Lev and Levi8], it is possible to use in [Pri], [OpI], and [Unif] bounded formulas instead of our absolute formulas, and the ordinarily defined class of
![]() $\Sigma $
-formulas instead of our somewhat bigger class.
$\Sigma $
-formulas instead of our somewhat bigger class.
Note 4.8. Actually, the use of [PrI] does not really increase the power of
![]() $\mathbf {PW}$
, and so we can omit it from
$\mathbf {PW}$
, and so we can omit it from
![]() $\mathbf {PW}$
. However, it is very convenient to include it.
$\mathbf {PW}$
. However, it is very convenient to include it.
4.2
 $\mathbf {PW}$
and
$\mathbf {PW}$
and
 $\mathbf {ZF}-(P)$
$\mathbf {ZF}-(P)$
In this section we prove that
![]() $\mathbf {PW}$
is a subsystem of (an extension by definitions of)
$\mathbf {PW}$
is a subsystem of (an extension by definitions of)
![]() $\mathbf {ZF}-(P)$
. It follows that every theorem of
$\mathbf {ZF}-(P)$
. It follows that every theorem of
![]() $\mathbf {PW}$
is acceptable to the ordinary mathematicians.
$\mathbf {PW}$
is acceptable to the ordinary mathematicians.
Definition 4.9. Let e be a term or a formula or an operation symbol of
![]() $\mathbf {PW}$
.
$\mathbf {PW}$
.
-
1.
 $\sigma _{e}$
is the minimal signature
$\sigma _{e}$
is the minimal signature
 $\sigma $
that satisfies the following conditions:
$\sigma $
that satisfies the following conditions:-
• It includes
 $\in $
and
$\in $
and
 $=$
.
$=$
. -
• It includes all the predicate symbols and operation symbols (including constants) that occur in e.
-
• If either
 $P_\psi $
or
$P_\psi $
or
 $F_\psi $
is in
$F_\psi $
is in
 $\sigma $
, then so are all the predicate symbols and operation symbols that occur in
$\sigma $
, then so are all the predicate symbols and operation symbols that occur in
 $\psi $
.
$\psi $
.
-
-
2. e is legal if the premises of [OpI] obtain whenever
 $F_{\varphi }$
is in
$F_{\varphi }$
is in
 $\sigma _{e}$
.
$\sigma _{e}$
. -
3. For legal e,
 $\mathbf {PW}_{e}$
is the set of all theorem of
$\mathbf {PW}_{e}$
is the set of all theorem of
 $\mathbf {PW}$
in the language of
$\mathbf {PW}$
in the language of
 $\sigma _{e}$
.
$\sigma _{e}$
.
Definition 4.10. Let e be legal. A structure
![]() $\mathcal {M}$
is adequate for e if:
$\mathcal {M}$
is adequate for e if:
-
•
 $\mathcal {M}$
is a structure for a signature that contains
$\mathcal {M}$
is a structure for a signature that contains
 $\sigma _{e}$
.
$\sigma _{e}$
. -
•
 $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
 $\mathbf {PW}_{e}$
.
$\mathbf {PW}_{e}$
.
Definition 4.11. Let
![]() $\mathcal {M}$
be a transitive set or class.
$\mathcal {M}$
be a transitive set or class.
![]() $\mathcal {M}^e$
is the structure for
$\mathcal {M}^e$
is the structure for
![]() $\sigma _{e}$
which is obtained from
$\sigma _{e}$
which is obtained from
![]() $\mathcal {M}$
by defining an interpretation
$\mathcal {M}$
by defining an interpretation
![]() $I_e$
of
$I_e$
of
![]() $\sigma _{e}$
in
$\sigma _{e}$
in
![]() $\mathcal {M}$
using the following recursive definition:
$\mathcal {M}$
using the following recursive definition:
-
•
 $\in ^{I_e}=\in $
.
$\in ^{I_e}=\in $
. -
•
 $P_{\psi }^{I_e}=[\vec {a}: \mathcal {M}^n\mid \mathcal {M}^e,\{\vec {v}:=\vec {a}\}\models \psi ]$
in case
$P_{\psi }^{I_e}=[\vec {a}: \mathcal {M}^n\mid \mathcal {M}^e,\{\vec {v}:=\vec {a}\}\models \psi ]$
in case
 $P_{\psi }$
is an n-ary predicate.
$P_{\psi }$
is an n-ary predicate. -
• If
 $F_{\psi }$
is an n-ary operation, then
$F_{\psi }$
is an n-ary operation, then
 $F_{\psi }^{I_e}[\vec {a}]$
is the unique
$F_{\psi }^{I_e}[\vec {a}]$
is the unique
 $b\in \mathcal {M}$
such that
$b\in \mathcal {M}$
such that
 $\mathcal {M}^e,\{\vec {v}:=\vec {a}\;; \;v_n:=b\}\models \psi $
in case such a unique b exists,
$\mathcal {M}^e,\{\vec {v}:=\vec {a}\;; \;v_n:=b\}\models \psi $
in case such a unique b exists,
 $\emptyset $
otherwise.
$\emptyset $
otherwise.
Theorem 4.12. Let
![]() $\mathcal {M}$
be a transitive model of
$\mathcal {M}$
be a transitive model of
![]() $\mathbf {ZF}-(P)$
, and let
$\mathbf {ZF}-(P)$
, and let
![]() $\theta $
be a formula of
$\theta $
be a formula of
![]() $\sigma _{e}$
. Suppose that
$\sigma _{e}$
. Suppose that
![]() $\theta \succ \{x_1,\ldots ,x_n\}$
where
$\theta \succ \{x_1,\ldots ,x_n\}$
where
![]() $n>0$
. Then the following collection is an element of
$n>0$
. Then the following collection is an element of
![]() $\mathcal {M}$
for every assignment
$\mathcal {M}$
for every assignment
![]() $\nu $
in
$\nu $
in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
Proof By induction on the structure of
![]() $\theta $
, using the relevant clauses in the definition of
$\theta $
, using the relevant clauses in the definition of
![]() $\succ $
.
$\succ $
.
-
• If
 $\theta $
is
$\theta $
is
 $x\neq x$
then
$x\neq x$
then
 $S_{\theta ,x}^{\nu }=\emptyset $
for every
$S_{\theta ,x}^{\nu }=\emptyset $
for every
 $\nu $
. Hence
$\nu $
. Hence
 $S_{\theta ,x}^{\nu }\in \mathcal {M}$
.
$S_{\theta ,x}^{\nu }\in \mathcal {M}$
. -
• If
 $\theta $
is
$\theta $
is
 $x\in t$
where
$x\in t$
where
 $x\not \in Fv(t)$
, then
$x\not \in Fv(t)$
, then
 $S_{\theta ,x}^{\nu }=\nu [t]$
(because
$S_{\theta ,x}^{\nu }=\nu [t]$
(because
 $\mathcal {M}$
is transitive). Hence
$\mathcal {M}$
is transitive). Hence
 $S_{\theta ,x}^{\nu }\in \mathcal {M}$
.
$S_{\theta ,x}^{\nu }\in \mathcal {M}$
. -
• If
 $\theta $
is
$\theta $
is
 $x=t$
where
$x=t$
where
 $x\not \in Fv(t)$
, then
$x\not \in Fv(t)$
, then
 $S_{\theta ,x}^{\nu }=\{\nu [t]\}$
. Hence
$S_{\theta ,x}^{\nu }=\{\nu [t]\}$
. Hence
 $S_{\theta ,x}^{\nu }\in \mathcal {M}$
by the pairing axiom.
$S_{\theta ,x}^{\nu }\in \mathcal {M}$
by the pairing axiom. -
• If
 $\theta $
is
$\theta $
is
 $\varphi \vee \psi $
, where
$\varphi \vee \psi $
, where
 $\varphi \succ \{x_1,\ldots \!,\! x_n\}$
and
$\varphi \succ \{x_1,\ldots \!,\! x_n\}$
and
 $\psi \succ \{x_1,\ldots \!,\! x_n\}$
, then
$\psi \succ \{x_1,\ldots \!,\! x_n\}$
, then
 $S_{\theta ,\vec {x}}^{\nu }=S_{\varphi ,\vec {x}}^{\nu }\cup S_{\psi ,\vec {x}}^{\nu }$
. Hence
$S_{\theta ,\vec {x}}^{\nu }=S_{\varphi ,\vec {x}}^{\nu }\cup S_{\psi ,\vec {x}}^{\nu }$
. Hence
 $S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
by the induction hypotheses for
$S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
by the induction hypotheses for
 $\varphi $
and
$\varphi $
and
 $\psi $
.
$\psi $
. -
• Suppose
 $\theta $
is
$\theta $
is
 $\varphi \wedge \psi $
, where
$\varphi \wedge \psi $
, where
 $\varphi \succ \{w_1,\ldots w_l\}$
,
$\varphi \succ \{w_1,\ldots w_l\}$
,
 $\psi \succ \{y_1,\ldots ,y_k\}$
,
$\psi \succ \{y_1,\ldots ,y_k\}$
,
 $n=l+k$
,
$n=l+k$
,
 $\{y_1,\ldots ,y_k\}\cap Fv(\varphi )=\emptyset $
, and
$\{y_1,\ldots ,y_k\}\cap Fv(\varphi )=\emptyset $
, and
 $\vec {x}=\langle w_1,\ldots w_l,y_1,\ldots ,y_k \rangle $
. We have three subcases to consider here.
$\vec {x}=\langle w_1,\ldots w_l,y_1,\ldots ,y_k \rangle $
. We have three subcases to consider here.-
–
 $k=0$
and
$k=0$
and
 $n=l$
. Then
$n=l$
. Then
 $S_{\theta ,\vec {x}}^{\nu }= [\vec {a}\in S_{\varphi ,\vec {x}}^{\nu }\mid \psi ]$
. Hence
$S_{\theta ,\vec {x}}^{\nu }= [\vec {a}\in S_{\varphi ,\vec {x}}^{\nu }\mid \psi ]$
. Hence
 $S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
by the induction hypothesis for
$S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
by the induction hypothesis for
 $\varphi $
and the separation axiom.
$\varphi $
and the separation axiom. -
–
 $l=0$
and
$l=0$
and
 $n=k$
. This case is similar to the previous one.
$n=k$
. This case is similar to the previous one. -
–
 $l>0$
and
$l>0$
and
 $k>0$
. To simplify notation, assume that
$k>0$
. To simplify notation, assume that
 $l=k=1$
,
$l=k=1$
,
 $Fv(\varphi )=\{w,z\}$
,
$Fv(\varphi )=\{w,z\}$
,
 $Fv(\psi )=\{w,y,z\}$
. For
$Fv(\psi )=\{w,y,z\}$
. For
 $c\in \mathcal {M}$
, let Since
$c\in \mathcal {M}$
, let Since $$ \begin{align*}Z(c)=[a\in \mathcal{M}\mid \mathcal{M}^e\models \varphi(a,c)].\end{align*} $$
$$ \begin{align*}Z(c)=[a\in \mathcal{M}\mid \mathcal{M}^e\models \varphi(a,c)].\end{align*} $$
 $\varphi \succ \{x\}$
,
$\varphi \succ \{x\}$
,
 $Z(c)\in \mathcal {M}$
by the induction hypothesis for
$Z(c)\in \mathcal {M}$
by the induction hypothesis for
 $\varphi $
. By the induction hypothesis for
$\varphi $
. By the induction hypothesis for
 $\psi $
, this and the fact that
$\psi $
, this and the fact that
 $\psi \succ \{y\}$
imply that
$\psi \succ \{y\}$
imply that
 $[b\in \mathcal {M}\mid \mathcal {M}^e\models \psi (d,b,c)]\in \mathcal {M}$
for every
$[b\in \mathcal {M}\mid \mathcal {M}^e\models \psi (d,b,c)]\in \mathcal {M}$
for every
 $c\in \mathcal {M}$
and
$c\in \mathcal {M}$
and
 $d\in Z(c)$
. Denote this set by
$d\in Z(c)$
. Denote this set by
 $W(c,d)$
. Then
$W(c,d)$
. Then
 $[\langle a,b \rangle \in \mathcal {M}^2\mid \mathcal {M}^e\models \theta (a,b,c)]$
equals
$[\langle a,b \rangle \in \mathcal {M}^2\mid \mathcal {M}^e\models \theta (a,b,c)]$
equals
 $\bigcup _{d\in Z(c)}\{d\}\times W(c,d)$
. Hence
$\bigcup _{d\in Z(c)}\{d\}\times W(c,d)$
. Hence
 $[\langle a,b \rangle \in \mathcal {M}^2\mid \mathcal {M}^e\models \theta (a,b,c)]\in \mathcal {M}$
by the axioms of replacement and union.
$[\langle a,b \rangle \in \mathcal {M}^2\mid \mathcal {M}^e\models \theta (a,b,c)]\in \mathcal {M}$
by the axioms of replacement and union.
-
-
• Suppose
 $\theta $
is
$\theta $
is
 $\exists y\varphi $
, where
$\exists y\varphi $
, where
 $\varphi \succ \{x_1,\ldots \!,\! x_n,y\}$
. Then Hence
$\varphi \succ \{x_1,\ldots \!,\! x_n,y\}$
. Then Hence $$ \begin{align*}S_{\theta,\vec{x}}^{\nu}=[\vec{a}\in \mathcal{M}^n\mid \exists b\in M.\langle a_1,\ldots,a_n,b \rangle\in S_{\varphi,\vec{x}}^{\nu}].\end{align*} $$
$$ \begin{align*}S_{\theta,\vec{x}}^{\nu}=[\vec{a}\in \mathcal{M}^n\mid \exists b\in M.\langle a_1,\ldots,a_n,b \rangle\in S_{\varphi,\vec{x}}^{\nu}].\end{align*} $$
 $S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
, by the induction hypothesis for
$S_{\theta ,\vec {x}}^{\nu }\in \mathcal {M}$
, by the induction hypothesis for
 $\varphi $
and the fact that
$\varphi $
and the fact that
 $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
 $\mathbf {Z}-(P)$
(and so is closed under the projection operation).
$\mathbf {Z}-(P)$
(and so is closed under the projection operation).
Corollary 4.13. From a platonist point of view, every collection which is defined by [Comp] is set (i.e., an element of the platonist universe
![]() $\mathsf {V}$
).
$\mathsf {V}$
).
Proof
![]() $\mathsf {V}$
is (believed to be) a model of
$\mathsf {V}$
is (believed to be) a model of
![]() $\mathbf {Z}-(P)$
. Hence Theorem 4.12 applies.
$\mathbf {Z}-(P)$
. Hence Theorem 4.12 applies.
Note 4.14. Another platonist collection which is known to be a model of
![]() $\mathbf {Z}-(P)$
is
$\mathbf {Z}-(P)$
is
![]() $\mathsf {HC}$
(the collection of hereditarily countable sets). From Theorem 4.24 it follows that if
$\mathsf {HC}$
(the collection of hereditarily countable sets). From Theorem 4.24 it follows that if
![]() $\theta \succ \{x_1 ,\ldots \!,\! x_n\}$
then the collection
$\theta \succ \{x_1 ,\ldots \!,\! x_n\}$
then the collection
![]() $S_{\theta ,\vec {x}}^{\nu }$
is the same in
$S_{\theta ,\vec {x}}^{\nu }$
is the same in
![]() $\mathsf {V}$
and in
$\mathsf {V}$
and in
![]() $\mathsf {HC}$
for every assignment
$\mathsf {HC}$
for every assignment
![]() $\nu $
in
$\nu $
in
![]() $\mathsf {HC}$
. Hence it is countable for every such
$\mathsf {HC}$
. Hence it is countable for every such
![]() $\nu $
.
$\nu $
.
Theorem 4.15. Every transitive model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathbf {Z}-(P)$
can be expanded to a model of
$\mathbf {Z}-(P)$
can be expanded to a model of
![]() $\mathbf {PW}$
.
$\mathbf {PW}$
.
Proof Obviously, the recursive definition given in Definition 4.11 can be extended to provide an expansion of
![]() $\mathcal {M}$
to a structure
$\mathcal {M}$
to a structure
![]() $\mathcal {M}^{\mathbf {PW}}$
for the language of
$\mathcal {M}^{\mathbf {PW}}$
for the language of
![]() $\mathbf {PW}$
. Now the axiom [Comp] is valid in this structure by Theorem 4.12, while the validity of [Unif] follows from the fact that if we replace this rule by the corresponding implication, we get a schema which is equivalent (in ZF without powerset and replacement) to the replacement schema. Hence [Unif] is valid in
$\mathbf {PW}$
. Now the axiom [Comp] is valid in this structure by Theorem 4.12, while the validity of [Unif] follows from the fact that if we replace this rule by the corresponding implication, we get a schema which is equivalent (in ZF without powerset and replacement) to the replacement schema. Hence [Unif] is valid in
![]() $\mathcal {M}^{\mathbf {PW}}$
. That all other axioms and rules of
$\mathcal {M}^{\mathbf {PW}}$
. That all other axioms and rules of
![]() $\mathbf {PW}$
are valid there is obvious.
$\mathbf {PW}$
are valid there is obvious.
Corollary 4.16.
![]() $\mathsf {HC}$
is a model of
$\mathsf {HC}$
is a model of
![]() $\mathbf {PW}$
. (More precisely,
$\mathbf {PW}$
. (More precisely,
![]() $\mathsf {HC}$
can be expanded to such a model.)
$\mathsf {HC}$
can be expanded to such a model.)
Theorem 4.17.
![]() $\mathbf {PW}$
is equivalent to a subsystem of
$\mathbf {PW}$
is equivalent to a subsystem of
![]() $\mathbf {ZF}-(P)$
.
$\mathbf {ZF}-(P)$
.
Proof This easily follows from Theorem 4.15 using ZF and model-theoretic methods. Alternative (and also predicatively acceptable) method is to turn the proof of Theorem 4.12 to a proof that every theorem of
![]() $\mathbf {PW}$
is provable in (an extension by definition of)
$\mathbf {PW}$
is provable in (an extension by definition of)
![]() $\mathbf {ZF}-(P)$
. This is not difficult. That the other axioms and rules of
$\mathbf {ZF}-(P)$
. This is not difficult. That the other axioms and rules of
![]() $\mathbf {PW}$
are derivable in
$\mathbf {PW}$
are derivable in
![]() $\mathbf {ZF}-(P)$
is (almost) obvious.
$\mathbf {ZF}-(P)$
is (almost) obvious.
4.3 Predicative justification of
 $\mathbf {PW}$
$\mathbf {PW}$
From the non-logical axioms and rules of
![]() $\mathbf {PW}$
, [Ext] and [PrI] need no justification, while [Inf] was justified in Section 3. It remains to justify the other non-logical axioms and rules of
$\mathbf {PW}$
, [Ext] and [PrI] need no justification, while [Inf] was justified in Section 3. It remains to justify the other non-logical axioms and rules of
![]() $\mathbf {PW}$
.
$\mathbf {PW}$
.
4.3.1 [Comp] and [OpI]
Theorem 4.12 alone is not sufficient for justifying [Comp]. In order to really justify this axiom from a predicative point of view, we should show that the identity of the sets it defines is invariant. Similarly, in order to justify [OpI] we should show that the operation defined by it is invariant. The first step towards these goals is to provide a precise notion of invariance which is adequate for the set-theoretical context.
Obviously, talking about invariance of definitions of sets and operations, when we expand one sphere of operation
![]() $\mathcal {M}_1$
to a bigger one
$\mathcal {M}_1$
to a bigger one
![]() $\mathcal {M}_2$
, can make sense only if the identities of the elements of
$\mathcal {M}_2$
, can make sense only if the identities of the elements of
![]() $\mathcal {M}_1$
are preserved in
$\mathcal {M}_1$
are preserved in
![]() $\mathcal {M}_2$
. Since in the context of set theory we take the identity of a set to be fully determined by the identity of its elements, this means that the same objects should belong to an element a of
$\mathcal {M}_2$
. Since in the context of set theory we take the identity of a set to be fully determined by the identity of its elements, this means that the same objects should belong to an element a of
![]() $\mathcal {M}_1$
in both
$\mathcal {M}_1$
in both
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
. Accordingly, we define the following:
$\mathcal {M}_2$
. Accordingly, we define the following:
Definition 4.18. Let
![]() $\mathcal {M}_1=\langle \mathcal {D}_1,I_1 \rangle $
and
$\mathcal {M}_1=\langle \mathcal {D}_1,I_1 \rangle $
and
![]() $\mathcal {M}_2=\langle \mathcal {D}_2,I_2 \rangle $
be structures for signatures that contain
$\mathcal {M}_2=\langle \mathcal {D}_2,I_2 \rangle $
be structures for signatures that contain
![]() $\in $
, and let both be models of [Ext].
$\in $
, and let both be models of [Ext].
![]() $\mathcal {M}_2$
is an
$\mathcal {M}_2$
is an
![]() $\in $
-extension of
$\in $
-extension of
![]() $\mathcal {M}_1$
if
$\mathcal {M}_1$
if
![]() $\mathcal {D}_1\subseteq \mathcal {D}_2$
, and the following holds for every element a of
$\mathcal {D}_1\subseteq \mathcal {D}_2$
, and the following holds for every element a of
![]() $\mathcal {D}_1$
:
$\mathcal {D}_1$
:
Note 4.19. From a platonistic point of view, if
![]() $\in ^{I_1}$
and
$\in ^{I_1}$
and
![]() $\in ^{I_2}$
are both the ‘real’
$\in ^{I_2}$
are both the ‘real’
![]() $\in $
of
$\in $
of
![]() $\mathsf {V}$
, then
$\mathsf {V}$
, then
![]() $\mathcal {M}_2$
is an
$\mathcal {M}_2$
is an
![]() $\in $
-extension of
$\in $
-extension of
![]() $\mathcal {M}_1$
iff
$\mathcal {M}_1$
iff
![]() $\mathcal {D}_1$
is a transitive subset of
$\mathcal {D}_1$
is a transitive subset of
![]() $\mathcal {D}_2$
.
$\mathcal {D}_2$
.
Definition 4.20. For legal e,
![]() $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an e-pair if:
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an e-pair if:
-
•
 $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
 $\mathcal {M}_2$
are adequate for e.
$\mathcal {M}_2$
are adequate for e. -
•
 $\mathcal {M}_2$
is an
$\mathcal {M}_2$
is an
 $\in $
-extension of
$\in $
-extension of
 $\mathcal {M}_1$
.
$\mathcal {M}_1$
. -
•
 $[a\in \mathcal {D}_2\mid \mathcal {M}_2\models N(a)]=[a\in \mathcal {D}_1\mid \mathcal {M}_1\models N(a)].$
$[a\in \mathcal {D}_2\mid \mathcal {M}_2\models N(a)]=[a\in \mathcal {D}_1\mid \mathcal {M}_1\models N(a)].$
Definition 4.21.
-
1. A legal term t of
 $\mathbf {PW}$
is invariant if
$\mathbf {PW}$
is invariant if
 $\nu _{\mathcal {M}_1}[t]=\nu _{\mathcal {M}_2}[t]$
whenever
$\nu _{\mathcal {M}_1}[t]=\nu _{\mathcal {M}_2}[t]$
whenever
 $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a t-pair, and
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a t-pair, and
 $\nu $
is an assignment in
$\nu $
is an assignment in
 $\mathcal {M}_1$
.
$\mathcal {M}_1$
. -
2. A legal n-ary operation F of
 $\mathbf {PW}$
is invariant if
$\mathbf {PW}$
is invariant if  $$ \begin{align*}F^{\mathcal{M}_1}[a_1 ,\ldots\!,\! a_n]=F^{\mathcal{M}_2}[a_1 ,\ldots\!,\! a_n]\end{align*} $$
$$ \begin{align*}F^{\mathcal{M}_1}[a_1 ,\ldots\!,\! a_n]=F^{\mathcal{M}_2}[a_1 ,\ldots\!,\! a_n]\end{align*} $$
whenever
 $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an F-pair, and
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an F-pair, and
 $a_1 ,\ldots \!,\! a_n$
are elements of
$a_1 ,\ldots \!,\! a_n$
are elements of
 $\mathcal {M}_1$
.
$\mathcal {M}_1$
. -
3. A legal formula
 $\varphi $
of
$\varphi $
of
 $\mathbf {PW}$
such that
$\mathbf {PW}$
such that
 $\{x_1 ,\ldots \!,\! x_n\}\subseteq Fv(\varphi )$
is invariant with respect to
$\{x_1 ,\ldots \!,\! x_n\}\subseteq Fv(\varphi )$
is invariant with respect to
 $\{x_1 ,\ldots \!,\! x_n\}$
if the following holds for every assignment
$\{x_1 ,\ldots \!,\! x_n\}$
if the following holds for every assignment
 $\nu $
in
$\nu $
in
 $\mathcal {M}_1$
:
$\mathcal {M}_1$
:  $$ \begin{align*}[\vec{a}: \mathcal{D}_2^n\mid \mathcal{M}_2,\nu\{\vec{x}:=\vec{a}\}\models\varphi]= [\vec{a}: \mathcal{D}_1^n\mid \mathcal{M}_1,\nu\{\vec{x}:=\vec{a}\}\models\varphi].\end{align*} $$
$$ \begin{align*}[\vec{a}: \mathcal{D}_2^n\mid \mathcal{M}_2,\nu\{\vec{x}:=\vec{a}\}\models\varphi]= [\vec{a}: \mathcal{D}_1^n\mid \mathcal{M}_1,\nu\{\vec{x}:=\vec{a}\}\models\varphi].\end{align*} $$
-
4. A legal formula
 $\varphi $
of
$\varphi $
of
 $\mathbf {PW}$
is persistent if
$\mathbf {PW}$
is persistent if
 $\mathcal {M}_1,\nu \models \varphi $
implies that
$\mathcal {M}_1,\nu \models \varphi $
implies that
 ${\mathcal {M}_2,\nu \models \varphi }$
as well, whenever
${\mathcal {M}_2,\nu \models \varphi }$
as well, whenever
 $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a
 $\varphi $
-pair, and
$\varphi $
-pair, and
 $\nu $
is an assignment in
$\nu $
is an assignment in
 $\mathcal {M}_1$
.
$\mathcal {M}_1$
.
Note 4.22. The definition of invariability of formulas can also be formulated as follows: a legal formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbf {PW}$
such that
$\mathbf {PW}$
such that
![]() $Fv(\varphi )=\{x_1 ,\ldots \!,\! x_n,y_1 ,\ldots \!,\! y_k\}$
is invariant with respect to
$Fv(\varphi )=\{x_1 ,\ldots \!,\! x_n,y_1 ,\ldots \!,\! y_k\}$
is invariant with respect to
![]() $\{x_1 ,\ldots \!,\! x_n\}$
if the following holds whenever
$\{x_1 ,\ldots \!,\! x_n\}$
if the following holds whenever
![]() $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is a
![]() $\varphi $
-pair, and
$\varphi $
-pair, and
![]() $c_1, \ldots , c_k$
are elements of
$c_1, \ldots , c_k$
are elements of
![]() $\mathcal {M}_1$
:
$\mathcal {M}_1$
:
(where
![]() $\langle a_1 ,\ldots \!,\! a_n \rangle ^{\frown }\!\langle c_1 ,\ldots \!,\! c_k \rangle = \langle a_1 ,\ldots \!,\! a_n,c_1 ,\ldots \!,\! c_k \rangle $
.)
$\langle a_1 ,\ldots \!,\! a_n \rangle ^{\frown }\!\langle c_1 ,\ldots \!,\! c_k \rangle = \langle a_1 ,\ldots \!,\! a_n,c_1 ,\ldots \!,\! c_k \rangle $
.)
Note 4.23. Identifying
![]() $\langle \rangle $
with
$\langle \rangle $
with
![]() $\emptyset $
, we get that in case
$\emptyset $
, we get that in case
![]() $n=0$
, the collection
$n=0$
, the collection
![]() $[\vec {a}: \mathcal {D}^n\mid \mathcal {M}\models \varphi (\vec {a}^{\frown }\!\vec {c})]$
is either 1 (
$[\vec {a}: \mathcal {D}^n\mid \mathcal {M}\models \varphi (\vec {a}^{\frown }\!\vec {c})]$
is either 1 (
![]() $=\{\emptyset \}$
) or 0 (
$=\{\emptyset \}$
) or 0 (
![]() $=\emptyset $
), depending on whether
$=\emptyset $
), depending on whether
![]() $\mathcal {M}\models \varphi (\vec {c})$
or not. Hence invariance with respect to
$\mathcal {M}\models \varphi (\vec {c})$
or not. Hence invariance with respect to
![]() $\emptyset $
is simply absoluteness.
$\emptyset $
is simply absoluteness.
Convention. From now on, when we talk about terms, we shall mean legal terms. The same convention applies to formulas and operation symbols.
Theorem 4.24.
-
1. Every term t of
 $\mathbf {PW}$
is invariant.
$\mathbf {PW}$
is invariant. -
2. Every operation F of
 $\mathbf {PW}$
is invariant.
$\mathbf {PW}$
is invariant. -
3. If
 $\varphi \succ \{x_1 ,\ldots \!,\! x_n\}$
in
$\varphi \succ \{x_1 ,\ldots \!,\! x_n\}$
in
 $\mathbf {PW}$
then
$\mathbf {PW}$
then
 $\varphi $
is invariant with respect to
$\varphi $
is invariant with respect to
 $\{x_1 ,\ldots \!,\! x_n\}$
.
$\{x_1 ,\ldots \!,\! x_n\}$
. -
4. Every
 $\Sigma $
-formula of
$\Sigma $
-formula of
 $\mathbf {PW}$
is persistent.
$\mathbf {PW}$
is persistent.
Proof We prove all parts simultaneously, using induction on the complexity of e, where e is a term or a formula or an operation symbol of
![]() $\mathbf {PW}$
. Nevertheless, to facilitate reading and understanding, we split the various induction steps into groups that correspond to the four parts of the theorem.
$\mathbf {PW}$
. Nevertheless, to facilitate reading and understanding, we split the various induction steps into groups that correspond to the four parts of the theorem.
In what follows we assume that for every e we consider,
![]() $\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an e-pair (
$\langle \mathcal {M}_1,\mathcal {M}_2 \rangle $
is an e-pair (
![]() $\mathcal {M}_1=\langle \mathcal {D}_1,I_1 \rangle $
,
$\mathcal {M}_1=\langle \mathcal {D}_1,I_1 \rangle $
,
![]() $\mathcal {M}_2=\langle \mathcal {D}_2,I_2 \rangle $
), and
$\mathcal {M}_2=\langle \mathcal {D}_2,I_2 \rangle $
), and
![]() $\nu $
is an assignment in
$\nu $
is an assignment in
![]() $\mathcal {D}_1$
.
$\mathcal {D}_1$
.
-
Operations: Suppose that e is the n-ary operation symbol
 $F_{\varphi }$
. For convenience of presentation, assume that
$F_{\varphi }$
. For convenience of presentation, assume that
 $n=1$
. Let
$n=1$
. Let
 $a:\mathcal {D}_1$
, and let
$a:\mathcal {D}_1$
, and let
 $b=F_{\varphi }^{I_1}[a]$
. Since
$b=F_{\varphi }^{I_1}[a]$
. Since
 $\mathcal {M}_1$
is a model of
$\mathcal {M}_1$
is a model of
 $\mathbf {PW}_e$
, the legality of
$\mathbf {PW}_e$
, the legality of
 $F_{\varphi }$
and the rule [OpI] imply that
$F_{\varphi }$
and the rule [OpI] imply that
 $\mathcal {M}_1\models \varphi (\langle a,b \rangle )$
. Since
$\mathcal {M}_1\models \varphi (\langle a,b \rangle )$
. Since
 $\varphi $
should be a
$\varphi $
should be a
 $\Sigma $
-formula, the induction hypothesis for
$\Sigma $
-formula, the induction hypothesis for
 $\varphi $
implies that
$\varphi $
implies that
 $\mathcal {M}_2\models \varphi (\langle a,b \rangle )$
too. Since
$\mathcal {M}_2\models \varphi (\langle a,b \rangle )$
too. Since
 $\mathcal {M}_2$
is a model of
$\mathcal {M}_2$
is a model of
 $\mathbf {PW}_e$
, this in turn implies (with the help of [OpI]) that
$\mathbf {PW}_e$
, this in turn implies (with the help of [OpI]) that
 $b=F_{\varphi }^{I_2}[a]$
as well.
$b=F_{\varphi }^{I_2}[a]$
as well. -
Terms:
-
• The case where e is a variable is trivial.
-
• The case
 $e=\omega $
is immediate from the third item of Definition 4.20.
$e=\omega $
is immediate from the third item of Definition 4.20. -
• Suppose that e is the term
 $F_{\varphi }(s_1 ,\ldots \!,\! s_n)$
. Then
$F_{\varphi }(s_1 ,\ldots \!,\! s_n)$
. Then  $$ \begin{align*}\nu_{\mathcal{M}_1}[e]=F_{\varphi}^{I_1}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]\ \ \ \nu_{\mathcal{M}_2}[e]=F_{\varphi}^{I_2}[\nu_{\mathcal{M}_2}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_2}[s_n]].\end{align*} $$
$$ \begin{align*}\nu_{\mathcal{M}_1}[e]=F_{\varphi}^{I_1}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]\ \ \ \nu_{\mathcal{M}_2}[e]=F_{\varphi}^{I_2}[\nu_{\mathcal{M}_2}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_2}[s_n]].\end{align*} $$
Now from the induction hypothesis for
 $F_{\varphi }$
we get:
$F_{\varphi }$
we get:  $$\begin{align*}F_{\varphi}^{I_1}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]= F_{\varphi}^{I_2}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]\end{align*}$$
$$\begin{align*}F_{\varphi}^{I_1}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]= F_{\varphi}^{I_2}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]\end{align*}$$
while from the induction hypotheses for
 $s_1 ,\ldots \!,\! s_n$
we get that
$s_1 ,\ldots \!,\! s_n$
we get that  $$\begin{align*}F_{\varphi}^{I_2}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]= F_{\varphi}^{I_2}[\nu_{\mathcal{M}_2}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_2}[s_n]].\end{align*}$$
$$\begin{align*}F_{\varphi}^{I_2}[\nu_{\mathcal{M}_1}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_1}[s_n]]= F_{\varphi}^{I_2}[\nu_{\mathcal{M}_2}[s_1] ,\ldots\!,\! \nu_{\mathcal{M}_2}[s_n]].\end{align*}$$
It follows that
 $\nu _{\mathcal {M}_1}[e]=\nu _{\mathcal {M}_2}[e]$
.
$\nu _{\mathcal {M}_1}[e]=\nu _{\mathcal {M}_2}[e]$
.
-
-
The invariance relation:
 $\succ $
$\succ $
-
•
-
– To show the absoluteness (invariance with respect to
 $\emptyset $
) of
$\emptyset $
) of
 $s\in t$
, let
$s\in t$
, let
 $\nu $
be an assignment in
$\nu $
be an assignment in
 $\mathcal {M}_1$
. Assume first that
$\mathcal {M}_1$
. Assume first that
 $\mathcal {M}_1,\nu \models s\in t$
. Then
$\mathcal {M}_1,\nu \models s\in t$
. Then
 $\nu _{\mathcal {M}_1}[s]\in ^{I_1}\nu _{\mathcal {M}_1}[t]$
. It follows by the induction hypotheses for s and t and the fact that
$\nu _{\mathcal {M}_1}[s]\in ^{I_1}\nu _{\mathcal {M}_1}[t]$
. It follows by the induction hypotheses for s and t and the fact that
 $\mathcal {M}_2$
is an
$\mathcal {M}_2$
is an
 $\in $
-extension of
$\in $
-extension of
 $\mathcal {M}_1$
that
$\mathcal {M}_1$
that
 $\nu _{\mathcal {M}_2}[s]\in ^{I_2}\nu _{\mathcal {M}_2}[t]$
too. Hence
$\nu _{\mathcal {M}_2}[s]\in ^{I_2}\nu _{\mathcal {M}_2}[t]$
too. Hence
 $\mathcal {M}_2,\nu \models s\in t$
. The proof of the converse (i.e., that if
$\mathcal {M}_2,\nu \models s\in t$
. The proof of the converse (i.e., that if
 $\mathcal {M}_2,\nu \models s\in t$
then
$\mathcal {M}_2,\nu \models s\in t$
then
 $\mathcal {M}_1,\nu \models s\in t$
) is similar.
$\mathcal {M}_1,\nu \models s\in t$
) is similar. -
– We leave the simpler proof that
 $s=t$
is absolute to the reader.
$s=t$
is absolute to the reader. -
– The case
 $e=P_{\varphi }(t_1,\ldots \!,\! t_n)$
is immediate from the induction hypothesis for
$e=P_{\varphi }(t_1,\ldots \!,\! t_n)$
is immediate from the induction hypothesis for
 $\varphi $
, and the
$\varphi $
, and the
 $\varphi $
-instance of [PrI] (which is in
$\varphi $
-instance of [PrI] (which is in
 $\mathbf {PW}_e$
).
$\mathbf {PW}_e$
).
-
-
•
-
– That
 $x\neq x$
is invariant with respect to x follows from the fact that for every
$x\neq x$
is invariant with respect to x follows from the fact that for every
 $\mathcal {M}=\langle \mathcal {D},I \rangle $
and
$\mathcal {M}=\langle \mathcal {D},I \rangle $
and
 $\nu $
,
$\nu $
,
 $[a:\mathcal {D}\mid \mathcal {M},\nu \{x:=a\}\models x\neq x]=\emptyset $
.
$[a:\mathcal {D}\mid \mathcal {M},\nu \{x:=a\}\models x\neq x]=\emptyset $
. -
– Let e be the formula
 $x= t$
, where
$x= t$
, where
 $x\not \in Fv(t)$
. Then the collection
$x\not \in Fv(t)$
. Then the collection
 $[a\in \mathcal {D}_1\mid \mathcal {M}_1,\nu \{x:=a\}\models x=t]$
is the singleton of
$[a\in \mathcal {D}_1\mid \mathcal {M}_1,\nu \{x:=a\}\models x=t]$
is the singleton of
 $\nu _{\mathcal {M}_1}[t]$
, while
$\nu _{\mathcal {M}_1}[t]$
, while
 $[a\in \mathcal {D}_2\mid \mathcal {M}_2,\nu \{x:=a\}\models x=t]$
is the singleton of
$[a\in \mathcal {D}_2\mid \mathcal {M}_2,\nu \{x:=a\}\models x=t]$
is the singleton of
 $\nu _{\mathcal {M}_2}[t]$
. Hence the induction hypothesis for t implies that the two sets are equal.
$\nu _{\mathcal {M}_2}[t]$
. Hence the induction hypothesis for t implies that the two sets are equal. -
– Let e be the formula
 $x\in t$
, where
$x\in t$
, where
 $x\not \in Fv(t)$
. Then
$x\not \in Fv(t)$
. Then  $$ \begin{align*}[a\in\mathcal{D}_1\mid \mathcal{M}_1,\nu\{x:=a\}\models x\in t]=[a\in\mathcal{D}_1\mid a\in^{\mathcal{M}_1}\nu_{\mathcal{M}_1}[t]],\end{align*} $$
Since
$$ \begin{align*}[a\in\mathcal{D}_1\mid \mathcal{M}_1,\nu\{x:=a\}\models x\in t]=[a\in\mathcal{D}_1\mid a\in^{\mathcal{M}_1}\nu_{\mathcal{M}_1}[t]],\end{align*} $$
Since $$ \begin{align*}[a\in\mathcal{D}_2\mid \mathcal{M}_2,\nu\{x:=a\}\models x\in t]=[a\in\mathcal{D}_2\mid a\in^{\mathcal{M}_2}\nu_{\mathcal{M}_2}[t]].\end{align*} $$
$$ \begin{align*}[a\in\mathcal{D}_2\mid \mathcal{M}_2,\nu\{x:=a\}\models x\in t]=[a\in\mathcal{D}_2\mid a\in^{\mathcal{M}_2}\nu_{\mathcal{M}_2}[t]].\end{align*} $$
 $\nu _{\mathcal {M}_1}[t]=\nu _{\mathcal {M}_2}[t]$
by the induction hypothesis for t, these two equations and the fact that
$\nu _{\mathcal {M}_1}[t]=\nu _{\mathcal {M}_2}[t]$
by the induction hypothesis for t, these two equations and the fact that
 $\mathcal {M}_2$
is an
$\mathcal {M}_2$
is an
 $\in $
-extension of
$\in $
-extension of
 $\mathcal {M}_1$
imply:
$\mathcal {M}_1$
imply:  $$ \begin{align*}&[a\in\mathcal{D}_1\mid \mathcal{M}_1,\nu\{x:=a\}\models x\in t]\\&\quad=[a\in\mathcal{D}_2\mid \mathcal{M}_2,\nu\{x:=a\}\models x\in t].\end{align*} $$
$$ \begin{align*}&[a\in\mathcal{D}_1\mid \mathcal{M}_1,\nu\{x:=a\}\models x\in t]\\&\quad=[a\in\mathcal{D}_2\mid \mathcal{M}_2,\nu\{x:=a\}\models x\in t].\end{align*} $$
-
-
• The proof that if
 $\varphi $
is absolute then so is
$\varphi $
is absolute then so is
 $\neg \varphi $
is left to the reader.
$\neg \varphi $
is left to the reader. -
• Let e be
 $\varphi \vee \psi $
, where
$\varphi \vee \psi $
, where
 $\varphi \succ \{x_1,\ldots \!,\! x_n\}$
and
$\varphi \succ \{x_1,\ldots \!,\! x_n\}$
and
 $\psi \succ \{x_1,\ldots \!,\! x_n\}$
. Then the collection
$\psi \succ \{x_1,\ldots \!,\! x_n\}$
. Then the collection
 $[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \varphi \vee \psi ]$
is the union of
$[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \varphi \vee \psi ]$
is the union of
 $[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \varphi ]$
and
$[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \varphi ]$
and
 $[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \psi ]$
. A similar equation holds for
$[\vec {a}\in \mathcal {D}_1^n\mid \mathcal {M}_1,\nu \{\vec {x}:=\vec {a}\}\models \psi ]$
. A similar equation holds for
 $[\vec {a}\in \mathcal {D}_2^n\mid \mathcal {M}_2,\nu \{\vec {x}:=\vec {a}\}\models \varphi \vee \psi ]$
. The equality of these two collections follows therefore from the induction hypotheses for
$[\vec {a}\in \mathcal {D}_2^n\mid \mathcal {M}_2,\nu \{\vec {x}:=\vec {a}\}\models \varphi \vee \psi ]$
. The equality of these two collections follows therefore from the induction hypotheses for
 $\varphi $
and
$\varphi $
and
 $\psi $
.
$\psi $
. -
• Let e be
 $\theta =\varphi \wedge \psi $
, where
$\theta =\varphi \wedge \psi $
, where
 $\varphi \succ X$
,
$\varphi \succ X$
,
 $\psi \succ Y$
, and
$\psi \succ Y$
, and
 $Y\cap Fv(\varphi )=\emptyset $
. To simplify notation, assume that
$Y\cap Fv(\varphi )=\emptyset $
. To simplify notation, assume that
 $Fv(\varphi )=\{x,z\}$
,
$Fv(\varphi )=\{x,z\}$
,
 $Fv(\psi )=\{x,y,z\}$
,
$Fv(\psi )=\{x,y,z\}$
,
 $X=\{x\}$
,
$X=\{x\}$
,
 $Y=\{y\}$
. For
$Y=\{y\}$
. For
 $c\in \mathcal {D}_1$
, let
$c\in \mathcal {D}_1$
, let
 $Z(c)=[a\in \mathcal {D}_2\mid \mathcal {M}_2\models \varphi (a,c)]$
. Since
$Z(c)=[a\in \mathcal {D}_2\mid \mathcal {M}_2\models \varphi (a,c)]$
. Since
 $\varphi \succ X$
,
$\varphi \succ X$
,
 $Z(c)=[a\in \mathcal {D}_1\mid \mathcal {M}_1\models \varphi (a,c)]$
as well (by the induction hypothesis for
$Z(c)=[a\in \mathcal {D}_1\mid \mathcal {M}_1\models \varphi (a,c)]$
as well (by the induction hypothesis for
 $\varphi $
). Hence
$\varphi $
). Hence
 $Z(c)\subseteq \mathcal {D}_1$
. By the induction hypothesis for
$Z(c)\subseteq \mathcal {D}_1$
. By the induction hypothesis for
 $\psi $
, this and the fact that
$\psi $
, this and the fact that
 $\psi \succ Y$
imply that if
$\psi \succ Y$
imply that if
 $d\in Z(c)$
then Denote this set by
$d\in Z(c)$
then Denote this set by $$ \begin{align*}[b\in \mathcal{D}_2\mid \mathcal{M}_2\models \psi(d,b,c)]= [b\in \mathcal{D}_1\mid \mathcal{M}_1\models \psi(d,b,c)].\end{align*} $$
$$ \begin{align*}[b\in \mathcal{D}_2\mid \mathcal{M}_2\models \psi(d,b,c)]= [b\in \mathcal{D}_1\mid \mathcal{M}_1\models \psi(d,b,c)].\end{align*} $$
 $W(c,d)$
. Now both
$W(c,d)$
. Now both
 $[\langle a,b \rangle \in \mathcal {D}_2^2\mid \mathcal {M}_2\models \theta (a,b,c)]$
and
$[\langle a,b \rangle \in \mathcal {D}_2^2\mid \mathcal {M}_2\models \theta (a,b,c)]$
and
 $[\langle a,b \rangle \in \mathcal {D}_1^2\mid \mathcal {M}_1\models \theta (a,b,c)]$
equal
$[\langle a,b \rangle \in \mathcal {D}_1^2\mid \mathcal {M}_1\models \theta (a,b,c)]$
equal
 $\bigcup _{d\in Z(c)}\{d\}\times W(c,d)$
. Hence these two sets are the same (for every
$\bigcup _{d\in Z(c)}\{d\}\times W(c,d)$
. Hence these two sets are the same (for every
 $c\in \mathcal {D}_1$
).
$c\in \mathcal {D}_1$
).
-
• We leave to the reader the case
 $e=\exists y\varphi $
, where
$e=\exists y\varphi $
, where
 $\varphi \succ X$
and
$\varphi \succ X$
and
 $y\in X$
.
$y\in X$
.
-
•
-
 $\Sigma $
-formulas:
$\Sigma $
-formulas:-
• Invariance implies persistence. Hence if
 $\varphi $
is absolute then it is persistent by what we have shown above.
$\varphi $
is absolute then it is persistent by what we have shown above. -
• It is well known that persistence of formulas is closed under disjunction, conjunction, and existential quantification, so we leave to the reader the standard proofs of these cases.
-
• Suppose that
 $\theta $
is
$\theta $
is
 $\forall x(\varphi \to \psi )$
, where
$\forall x(\varphi \to \psi )$
, where
 $\varphi \succ \{x\}$
and
$\varphi \succ \{x\}$
and
 $\psi $
is a
$\psi $
is a
 $\Sigma $
-formula. By the induction hypothesis for
$\Sigma $
-formula. By the induction hypothesis for
 $\varphi $
and
$\varphi $
and
 $\psi $
,
$\psi $
,
 $\varphi $
is invariant with respect to x, and
$\varphi $
is invariant with respect to x, and
 $\psi $
is persistent. We show that
$\psi $
is persistent. We show that
 $\theta $
is persistent too. So let
$\theta $
is persistent too. So let
 $\nu $
be an assignment in
$\nu $
be an assignment in
 $\mathcal {M}_1$
such that
$\mathcal {M}_1$
such that
 $\mathcal {M}_1,\nu \models \theta $
. We show that
$\mathcal {M}_1,\nu \models \theta $
. We show that
 $\mathcal {M}_2,\nu \models \theta $
. So let
$\mathcal {M}_2,\nu \models \theta $
. So let
 $a\in \mathcal {D}_2$
. We should show that
$a\in \mathcal {D}_2$
. We should show that
 $\mathcal {M}_2,\nu \{x:=a\}\models \varphi \to \psi $
. This is certainly true in case
$\mathcal {M}_2,\nu \{x:=a\}\models \varphi \to \psi $
. This is certainly true in case
 $\mathcal {M}_2,\nu \{x:=a\}\not \models \varphi $
. So assume that
$\mathcal {M}_2,\nu \{x:=a\}\not \models \varphi $
. So assume that
 $\mathcal {M}_2,\nu \{x:=a\}\models \varphi $
. Then the invariability of
$\mathcal {M}_2,\nu \{x:=a\}\models \varphi $
. Then the invariability of
 $\varphi $
with respect to x implies that
$\varphi $
with respect to x implies that
 $a\in \mathcal {D}_1$
,
$a\in \mathcal {D}_1$
,
 $\nu \{x:=a\}$
is an assignment in
$\nu \{x:=a\}$
is an assignment in
 $\mathcal {D}_1$
, and
$\mathcal {D}_1$
, and
 $\mathcal {M}_1,\nu \{x:=a\}\models \varphi $
. Since
$\mathcal {M}_1,\nu \{x:=a\}\models \varphi $
. Since
 $\mathcal {M}_1,\nu \models \theta $
, also
$\mathcal {M}_1,\nu \models \theta $
, also
 $\mathcal {M}_1,\nu \{x:=a\}\models \varphi \to \psi $
. It follows that
$\mathcal {M}_1,\nu \{x:=a\}\models \varphi \to \psi $
. It follows that
 $\mathcal {M}_1,\nu \{x:=a\}\models \psi $
. This implies that
$\mathcal {M}_1,\nu \{x:=a\}\models \psi $
. This implies that
 $\mathcal {M}_2,\nu \{x:=a\}\models \psi $
, since
$\mathcal {M}_2,\nu \{x:=a\}\models \psi $
, since
 $\psi $
is persistent. It follows that
$\psi $
is persistent. It follows that
 $\mathcal {M}_2,\nu \{x:=a\}\models \varphi \to \psi $
in this case too.
$\mathcal {M}_2,\nu \{x:=a\}\models \varphi \to \psi $
in this case too.
-
Clearly, Theorem 4.24 provides the predicative justification of [Comp] (according to the invariance criterion) that Theorem 4.12 does not. As for [OpI], its premise ensures that
![]() $F_{\varphi }$
can be introduced using the usual procedure of extension by definitions. That the resulting operation is invariant follows again from Theorem 4.24.
$F_{\varphi }$
can be introduced using the usual procedure of extension by definitions. That the resulting operation is invariant follows again from Theorem 4.24.
4.3.2 [
 $\in $
-ind]
$\in $
-ind]
That [
![]() $\in $
-ind] is predicatively valid should be obvious: In any sphere of operation, the empty set is the starting building block of all sets, every other set A is formed from the elements of A, and those elements are logically prior to A. Therefore in any sphere of operation, a property that the empty set has and is inherited by a set from its elements should necessarily hold for all sets. Hence [
$\in $
-ind] is predicatively valid should be obvious: In any sphere of operation, the empty set is the starting building block of all sets, every other set A is formed from the elements of A, and those elements are logically prior to A. Therefore in any sphere of operation, a property that the empty set has and is inherited by a set from its elements should necessarily hold for all sets. Hence [
![]() $\in $
-ind] is valid in any acceptable sphere of operation.
$\in $
-ind] is valid in any acceptable sphere of operation.
Another way to look at the matter is by asking what properties the basic predicate
![]() $\in $
should have according to the predicativist view of sets. Since predicatively accepted sets are constructed bottom-up, it should be clear that the ‘well-foundedness’ of
$\in $
should have according to the predicativist view of sets. Since predicatively accepted sets are constructed bottom-up, it should be clear that the ‘well-foundedness’ of
![]() $\in $
should be one of those properties. But only the general, open-ended schema of [
$\in $
should be one of those properties. But only the general, open-ended schema of [
![]() $\in $
-ind] fully exploits what we really have in mind when we say that
$\in $
-ind] fully exploits what we really have in mind when we say that
![]() $\in $
should be well founded. (In contrast, the intuitive absoluteness of the well-foundness of
$\in $
should be well founded. (In contrast, the intuitive absoluteness of the well-foundness of
![]() $\in $
is not fully captured by any of the standard formal definitions of this notion.Footnote
20
For example, whether any subset of a given set A has a minimal element depends on what subsets of A are available, while the non-existence of a descending
$\in $
is not fully captured by any of the standard formal definitions of this notion.Footnote
20
For example, whether any subset of a given set A has a minimal element depends on what subsets of A are available, while the non-existence of a descending
![]() $\in $
-chain of elements of A depends on what sequences of elements of A are available.)
$\in $
-chain of elements of A depends on what sequences of elements of A are available.)
Still another point of view that might be taken here is that of a modest platonist who looks at the predicative spheres of operation. As was emphasized in Note 1.6 and shown in Theorem 4.17, in
![]() $\mathbf {PW}$
we restrict ourselves to predicative subsystems (of some extension by definitions) of
$\mathbf {PW}$
we restrict ourselves to predicative subsystems (of some extension by definitions) of
![]() $\mathbf {ZF}-(P)$
. Assuming that the latter is consistent, it is impossible to define in it a set which have elements that form an infinite descending chain with respect to
$\mathbf {ZF}-(P)$
. Assuming that the latter is consistent, it is impossible to define in it a set which have elements that form an infinite descending chain with respect to
![]() $\in $
. Hence this certainly cannot be done in more constrained predicative systems like
$\in $
. Hence this certainly cannot be done in more constrained predicative systems like
![]() $\mathbf {PW}$
.
$\mathbf {PW}$
.
Here it is worth noting that the predicativist conception of sets that underlies
![]() $\mathbf {PW}$
and the platonist cumulative one have a lot in common. According to both, all sets are created in stages, where the latter can be taken to be the von Neumann’s ordinals. (The difference is that according to predicativists, the “creation” is done by using legitimate definitions, while for platonists this can also be done by methods that go beyond what actual people can use.) Moreover, as we are going to see, both predicativists and platonists associate with every set A which is available to the former the same stage (called
$\mathbf {PW}$
and the platonist cumulative one have a lot in common. According to both, all sets are created in stages, where the latter can be taken to be the von Neumann’s ordinals. (The difference is that according to predicativists, the “creation” is done by using legitimate definitions, while for platonists this can also be done by methods that go beyond what actual people can use.) Moreover, as we are going to see, both predicativists and platonists associate with every set A which is available to the former the same stage (called
![]() $rank(A)$
) in which it first becomes available (even though the platonist set
$rank(A)$
) in which it first becomes available (even though the platonist set
![]() $\mathsf {V}_\alpha $
is available to predicativists only for
$\mathsf {V}_\alpha $
is available to predicativists only for
![]() $\alpha \leq \omega $
). It seems to me obvious that this view of sets that predicativists and platonists share dictates for both the validity of [
$\alpha \leq \omega $
). It seems to me obvious that this view of sets that predicativists and platonists share dictates for both the validity of [
![]() $\in $
-ind].
$\in $
-ind].
Two related notes:
-
1. In a private correspondence, Gerhard Jäger has raised two objections against accepting full [
 $\in $
-ind] as a predicatively accepted principle:
$\in $
-ind] as a predicatively accepted principle:-
• [
 $\in $
-ind] is a minimality condition on the universe and thus leads to an inherent vicious circle.
$\in $
-ind] is a minimality condition on the universe and thus leads to an inherent vicious circle.I do not share this view. In my opinion, [
 $\in $
-ind] is not a minimality condition, but only a constraint that our spheres of operation should respect. These are two different things. What is more: I believe (though this belief is not reflected in the present paper) that not all forms of ‘circularity’ should be rejected from the invariance point of view. Thus, although one might claim that all sorts of recursive definitions are inherently circular, some forms of them, like primitive recursive definitions, are certainly predicatively acceptable.
$\in $
-ind] is not a minimality condition, but only a constraint that our spheres of operation should respect. These are two different things. What is more: I believe (though this belief is not reflected in the present paper) that not all forms of ‘circularity’ should be rejected from the invariance point of view. Thus, although one might claim that all sorts of recursive definitions are inherently circular, some forms of them, like primitive recursive definitions, are certainly predicatively acceptable.In any case, the same argument can be raised against accepting the schema of induction on the natural numbers. However this general schema was accepted and used Weyl in [Reference Weyl52] (see [Reference Adams and Luo2, Reference Avron6]), and in fact it is accepted as predicative by almost everyone interested in the subject.
-
• In the form
 $\exists x \varphi [x] \to \exists x ( \varphi [x] \land (\forall y \in x)(\neg \varphi [y])$
the schema of [
$\exists x \varphi [x] \to \exists x ( \varphi [x] \land (\forall y \in x)(\neg \varphi [y])$
the schema of [
 $\in $
-ind] claims the existence of a set, without presenting an explicit definition of this set, and without ensuring that its identity is invariant.
$\in $
-ind] claims the existence of a set, without presenting an explicit definition of this set, and without ensuring that its identity is invariant.This issue has already been dealt with above in Note 1.5. As was emphasized there, every predicative system which is based on classical logic proves pure existential propositions of this sort, and there is nothing impredicative about that, as long as such propositions are understood and used in an appropriate way.
-
-
2. Although this is not really an acceptable argument for the predicative validity of [
 $\in $
-ind], it is still interesting to note that Feferman himself included this schema in the predicative set theories he constructed in [Reference Feferman, Scott and Jech18]. This clearly implies that he saw this schema as predicatively valid. In response one may argue that Feferman justified his set theories in [Reference Feferman, Scott and Jech18] only by reducing them to what he did in [Reference Feferman15]. However, Feferman did not take his set theories out of the blue; actually he too was led to them by pursuing the invariance criterion (see also [Reference Feferman17]). Hence the fact that he included [
$\in $
-ind], it is still interesting to note that Feferman himself included this schema in the predicative set theories he constructed in [Reference Feferman, Scott and Jech18]. This clearly implies that he saw this schema as predicatively valid. In response one may argue that Feferman justified his set theories in [Reference Feferman, Scott and Jech18] only by reducing them to what he did in [Reference Feferman15]. However, Feferman did not take his set theories out of the blue; actually he too was led to them by pursuing the invariance criterion (see also [Reference Feferman17]). Hence the fact that he included [
 $\in $
-ind] already in the system
$\in $
-ind] already in the system
 $\mathbf {PS}_0$
, which is by far the weakest system studied in [Reference Feferman, Scott and Jech18], is telling. Moreover, Feferman explicitly said about the system PS that he studied in [Reference Feferman16] (note the name of that paper!) that an ideal predicativist can recognize as correct any particular axiom and rule of inference of that system. Since any instance of [
$\mathbf {PS}_0$
, which is by far the weakest system studied in [Reference Feferman, Scott and Jech18], is telling. Moreover, Feferman explicitly said about the system PS that he studied in [Reference Feferman16] (note the name of that paper!) that an ideal predicativist can recognize as correct any particular axiom and rule of inference of that system. Since any instance of [
 $\in $
-ind] can be derived from the axioms and rules of PS, this means that according to Feferman a predicativist can recognize as correct any instance of [
$\in $
-ind] can be derived from the axioms and rules of PS, this means that according to Feferman a predicativist can recognize as correct any instance of [
 $\in $
-ind].
$\in $
-ind].
A final remark: personally, I have no doubt that the answer to the question whether [
![]() $\in $
-ind] is predicatively valid is positive, and that the arguments given above for this answer should be convincing (and would be accepted as such by Weyl and even Feferman). However, this question is not a mathematical one, and so some people might have different views on this point. Since I see debates on the exact meaning of a given word as useless, I simply take such conflicting views as indicating that like ‘predicativity’ in general, also ‘predicativity as invariance’ is a family of approaches to the foundations of mathematics. I would be quite happy to call mine ‘predicativity given that
$\in $
-ind] is predicatively valid is positive, and that the arguments given above for this answer should be convincing (and would be accepted as such by Weyl and even Feferman). However, this question is not a mathematical one, and so some people might have different views on this point. Since I see debates on the exact meaning of a given word as useless, I simply take such conflicting views as indicating that like ‘predicativity’ in general, also ‘predicativity as invariance’ is a family of approaches to the foundations of mathematics. I would be quite happy to call mine ‘predicativity given that
![]() $\in $
is well-founded’.
$\in $
is well-founded’.
4.3.3 [Unif]
Let
![]() $\varphi $
be
$\varphi $
be
![]() $\Sigma $
. For convenience, let
$\Sigma $
. For convenience, let
![]() $Fv(\varphi )=\{x,y\}$
. Suppose that at a certain point of working in
$Fv(\varphi )=\{x,y\}$
. Suppose that at a certain point of working in
![]() $\mathbf {PW}$
we have reached a stage
$\mathbf {PW}$
we have reached a stage
![]() $\mathsf {s}$
in which the premise of [Unif] has been derived. Then from that point on it is valid in any sphere of operation that we reach. Let a be an object in some such sphere of operation. If
$\mathsf {s}$
in which the premise of [Unif] has been derived. Then from that point on it is valid in any sphere of operation that we reach. Let a be an object in some such sphere of operation. If
![]() $\forall x\in Z\exists y \varphi $
is false for
$\forall x\in Z\exists y \varphi $
is false for
![]() $Z:=a$
in every sphere of operation that includes a which is reached at stage
$Z:=a$
in every sphere of operation that includes a which is reached at stage
![]() $\mathsf {s}$
or later, then certainly the corresponding conclusion of [Unif] is valid in all such spheres. Otherwise there is a stage
$\mathsf {s}$
or later, then certainly the corresponding conclusion of [Unif] is valid in all such spheres. Otherwise there is a stage
![]() $\mathsf {s}^\prime $
in which
$\mathsf {s}^\prime $
in which
![]() $\forall x\in Z\exists y \varphi $
is true for
$\forall x\in Z\exists y \varphi $
is true for
![]() $Z:=a$
. Since
$Z:=a$
. Since
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma $
, so is
$\Sigma $
, so is
![]() $\forall x\in Z\exists y \varphi $
. Hence Theorem 4.24 implies that
$\forall x\in Z\exists y \varphi $
. Hence Theorem 4.24 implies that
![]() $\forall x\in Z\exists y \varphi $
remains true for
$\forall x\in Z\exists y \varphi $
remains true for
![]() $Z:=a$
at any stage from
$Z:=a$
at any stage from
![]() $\mathsf {s}^\prime $
on. This and the validity of the premise of [Unif] in the sphere of operation
$\mathsf {s}^\prime $
on. This and the validity of the premise of [Unif] in the sphere of operation
![]() $\mathcal {M}$
of each such stage imply that the collection of pairs
$\mathcal {M}$
of each such stage imply that the collection of pairs
![]() $\langle c,d \rangle $
such that
$\langle c,d \rangle $
such that
![]() $c\in a$
and
$c\in a$
and
![]() $\langle c,d \rangle $
satisfies
$\langle c,d \rangle $
satisfies
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal {M}$
forms (‘in
$\mathcal {M}$
forms (‘in
![]() $\mathsf {V}$
’) a function f on a. From the fact that
$\mathsf {V}$
’) a function f on a. From the fact that
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma $
it again follows that as a collection of pairs f remains invariant. Therefore f is entitled to be added at some stage to the sphere of operation of that stage, and from that point the corresponding instance of [Unif] remains valid.
$\Sigma $
it again follows that as a collection of pairs f remains invariant. Therefore f is entitled to be added at some stage to the sphere of operation of that stage, and from that point the corresponding instance of [Unif] remains valid.
Note 4.25. The only justification given by Feferman in [Reference Feferman and Lorenz19] for the version of [Unif] which is used in his auxiliary system
![]() $\exists /P$
is that he does not believe there can be a real dispute about it. However, one might wonder why his rule cannot simply be replaced by an axiom stating that its premise implies its conclusion (both without the ‘
$\exists /P$
is that he does not believe there can be a real dispute about it. However, one might wonder why his rule cannot simply be replaced by an axiom stating that its premise implies its conclusion (both without the ‘
![]() $\vdash $
’ in front). Why could there be a real dispute about this implication, but not about the rule? The answer is clear from the argument given above: For the truth of the conclusion of the rule for some a in some
$\vdash $
’ in front). Why could there be a real dispute about this implication, but not about the rule? The answer is clear from the argument given above: For the truth of the conclusion of the rule for some a in some
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \forall x\in Z\exists y \varphi $
holds in
$ \forall x\in Z\exists y \varphi $
holds in
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $Z:=a$
, it is crucial that the premise of the rule (i.e., the unicity condition) remains valid in any sphere of operation that contains
$Z:=a$
, it is crucial that the premise of the rule (i.e., the unicity condition) remains valid in any sphere of operation that contains
![]() $\mathcal {M}$
; its truth just at
$\mathcal {M}$
; its truth just at
![]() $\mathcal {M}$
itself is insufficient.
$\mathcal {M}$
itself is insufficient.
4.4 Comparison with Feferman’s systems
The design of
![]() $\mathbf {PW}$
has a lot in common with - and was greatly influenced by - the second-order system
$\mathbf {PW}$
has a lot in common with - and was greatly influenced by - the second-order system
![]() $P+\exists /P$
for predicative analysis that Feferman has developed in [Reference Feferman and Lorenz19]. In particular:
$P+\exists /P$
for predicative analysis that Feferman has developed in [Reference Feferman and Lorenz19]. In particular:
-
• In practice, neither
 $\mathbf {PW}$
nor
$\mathbf {PW}$
nor
 $P+\exists /P$
has a signature which is fixed in advance, and the method of repeatedly extending the language and adding new corresponding axioms is an essential component of the work in both.
$P+\exists /P$
has a signature which is fixed in advance, and the method of repeatedly extending the language and adding new corresponding axioms is an essential component of the work in both. -
• The definitions of both systems involve a simultaneous recursive construction of their sets of symbols, terms, formulas, axioms, and rules.
-
• The two special rules of
 $\mathbf {PW}$
, [OpI] and [Unif], which (as is shown below) give this system its strong power (far beyond that of the systems
$\mathbf {PW}$
, [OpI] and [Unif], which (as is shown below) give this system its strong power (far beyond that of the systems
 $\mathbf {RST}\omega $
and
$\mathbf {RST}\omega $
and
 $\mathbf {PZF}$
investigated in [Reference Avron and Schindler5, Reference Avron and Cohen7, Reference Cohen and Avron10]), generalize (respectively) to set theory the following two rules from [Reference Feferman and Lorenz19]:
$\mathbf {PZF}$
investigated in [Reference Avron and Schindler5, Reference Avron and Cohen7, Reference Cohen and Avron10]), generalize (respectively) to set theory the following two rules from [Reference Feferman and Lorenz19]: -
Functional defining rule: This rule allows to infer
from the premises $$ \begin{align*}\vdash_P\forall v_1\forall v_0(\varphi(v_1,v_0)\leftrightarrow v_0=F_\varphi(v_1))\end{align*} $$
$$ \begin{align*}\vdash_P\forall v_1\forall v_0(\varphi(v_1,v_0)\leftrightarrow v_0=F_\varphi(v_1))\end{align*} $$
 $\vdash _P \forall v_1\forall v_2\forall v_3(\varphi (v_1,v_2)\wedge \varphi (v_1,v_3)\to v_2=v_3)$
and
$\vdash _P \forall v_1\forall v_2\forall v_3(\varphi (v_1,v_2)\wedge \varphi (v_1,v_3)\to v_2=v_3)$
and
 $\vdash _{\exists /P}\forall v_1\exists v_0\varphi (v_1,v_0)$
, provided that
$\vdash _{\exists /P}\forall v_1\exists v_0\varphi (v_1,v_0)$
, provided that
 $\varphi $
is a formula in which quantification is made only over the lowest type N (implying that
$\varphi $
is a formula in which quantification is made only over the lowest type N (implying that
 $\varphi $
is absolute).
$\varphi $
is absolute).
-
Unification rule: This rule allows to infer
from $$ \begin{align*}\vdash_{\exists/P} \forall v_1\in\mathbf{N}\exists v_0\varphi(v_1,v_0)\to\exists f\forall v_1\in\mathbf{N}\varphi(v_1,f(v_1))\end{align*} $$
$$ \begin{align*}\vdash_{\exists/P} \forall v_1\in\mathbf{N}\exists v_0\varphi(v_1,v_0)\to\exists f\forall v_1\in\mathbf{N}\varphi(v_1,f(v_1))\end{align*} $$
 $\vdash _P \forall v_1\in \mathbf {N}\forall v_2\forall v_3(\varphi (v_1,v_2)\wedge \varphi (v_1,v_3)\to v_2=v_3)$
, provided that
$\vdash _P \forall v_1\in \mathbf {N}\forall v_2\forall v_3(\varphi (v_1,v_2)\wedge \varphi (v_1,v_3)\to v_2=v_3)$
, provided that
 $\varphi $
is a formula in which quantification is made only over N.
$\varphi $
is a formula in which quantification is made only over N.
It should be noted that a preliminary version, called [F], of a combination of [OpI] and [Unif] appears already in the last section of [Reference Feferman15], where predicativity at higher types is discussed. [F] allows to infer from
 $\forall x\exists ! y \varphi (x,y)$
the formula
$\forall x\exists ! y \varphi (x,y)$
the formula
 $\exists f\forall x\forall y(\varphi (x,y)\leftrightarrow y=f(x))$
, provided that
$\exists f\forall x\forall y(\varphi (x,y)\leftrightarrow y=f(x))$
, provided that
 $\varphi $
is a
$\varphi $
is a
 $\Sigma $
-formula. (Note that unlike in the present context of type-free set theory, in [F] the variable f is of type higher than that of x.) The rule [F] was then implicitly split in [Reference Feferman and Lorenz19] into the two rules described above.
$\Sigma $
-formula. (Note that unlike in the present context of type-free set theory, in [F] the variable f is of type higher than that of x.) The rule [F] was then implicitly split in [Reference Feferman and Lorenz19] into the two rules described above. -
Nevertheless, there are also important differences between
![]() $\mathbf {PW}$
and
$\mathbf {PW}$
and
![]() ${P+\exists /P}$
:
${P+\exists /P}$
:
-
1.
 $\mathbf {PW}$
is a single system. In contrast,
$\mathbf {PW}$
is a single system. In contrast,
 $P+\exists /P$
is a combination of two different ones: P and
$P+\exists /P$
is a combination of two different ones: P and
 $\exists /P$
. P is taken to be the major system, while the stronger system
$\exists /P$
. P is taken to be the major system, while the stronger system
 $\exists /P$
is taken to be only an auxiliary one, which is needed for the precise definition of P. The connection between these two systems involves some choices for which no justification is given in [Reference Feferman and Lorenz19]. (See Weaver’s criticism, with which I fully agree, in Section 1.6 of [Reference Weaver50].) We believe, in fact (though we have not tried to show), that with different (but still predicatively justified) choices,
$\exists /P$
is taken to be only an auxiliary one, which is needed for the precise definition of P. The connection between these two systems involves some choices for which no justification is given in [Reference Feferman and Lorenz19]. (See Weaver’s criticism, with which I fully agree, in Section 1.6 of [Reference Weaver50].) We believe, in fact (though we have not tried to show), that with different (but still predicatively justified) choices,
 $P+\exists /P$
can be strengthened to a single theory which is as strong as
$P+\exists /P$
can be strengthened to a single theory which is as strong as
 $\mathbf {PW}$
.
$\mathbf {PW}$
. -
2. P and
 $\exists /P$
are based on an extensive system of types, which has types of all finite levels (but actually uses only those of levels 0, 1, and 2).
$\exists /P$
are based on an extensive system of types, which has types of all finite levels (but actually uses only those of levels 0, 1, and 2).
 $\mathbf {PW}$
, in contrast, is a type-free, single-sorted set theory.
$\mathbf {PW}$
, in contrast, is a type-free, single-sorted set theory. -
3. Unlike
 $\mathbf {PW}$
, which is purely first-order, P and
$\mathbf {PW}$
, which is purely first-order, P and
 $\exists /P$
have second-order variables in addition to the first-order ones. In the case of
$\exists /P$
have second-order variables in addition to the first-order ones. In the case of
 $\exists /P$
it is even allowed (under certain conditions) to quantify on them. Moreover, both systems employ specific second-order rules, like substitution of terms, and even (again under certain conditions) of formulas, for second-order variables. (No rule of substitution is needed in the case of
$\exists /P$
it is even allowed (under certain conditions) to quantify on them. Moreover, both systems employ specific second-order rules, like substitution of terms, and even (again under certain conditions) of formulas, for second-order variables. (No rule of substitution is needed in the case of
 $\mathbf {PW}$
.)
$\mathbf {PW}$
.) -
4. The set of natural numbers is taken as given in P. In
 $\mathbf {PW}$
it is defined.
$\mathbf {PW}$
it is defined.
Note 4.26. Because of these differences, and because
![]() $\mathbf {PW}$
has simpler language and less rules than
$\mathbf {PW}$
has simpler language and less rules than
![]() $P+\exists /P$
, we believe that it is fair to say that
$P+\exists /P$
, we believe that it is fair to say that
![]() $\mathbf {PW}$
is significantly simpler then
$\mathbf {PW}$
is significantly simpler then
![]() $P+\exists /P$
. The latter, in turn, is according to Feferman himself more perspicuous than the original predicative systems of [Reference Feferman15]. These observations justify the claim made at the beginning of Note 1.8.
$P+\exists /P$
. The latter, in turn, is according to Feferman himself more perspicuous than the original predicative systems of [Reference Feferman15]. These observations justify the claim made at the beginning of Note 1.8.
Other systems of Feferman which are obviously related to
![]() $\mathbf {PW}$
are the pure set theories
$\mathbf {PW}$
are the pure set theories
![]() $\mathbf {PS_i}$
and
$\mathbf {PS_i}$
and
![]() $\mathbf {PS_iE}$
(
$\mathbf {PS_iE}$
(
![]() $i=0,1$
) which were introduced in [Reference Feferman, Scott and Jech18] (see Note 1.4). Like
$i=0,1$
) which were introduced in [Reference Feferman, Scott and Jech18] (see Note 1.4). Like
![]() $\mathbf {PW}$
, they too are intuitively motivated by the invariance criterion, and so
$\mathbf {PW}$
, they too are intuitively motivated by the invariance criterion, and so
![]() $\Sigma $
-formulas and absolute formulas play an important role in their formulation. Accordingly, those systems are less restricted than the second-order systems of [Reference Feferman15]. Thus the union operation is allowed in them, although it is taken as impredicative in most of Feferman’s papers.Footnote
21
On the other hand, unlike
$\Sigma $
-formulas and absolute formulas play an important role in their formulation. Accordingly, those systems are less restricted than the second-order systems of [Reference Feferman15]. Thus the union operation is allowed in them, although it is taken as impredicative in most of Feferman’s papers.Footnote
21
On the other hand, unlike
![]() $\mathbf {PW}$
, none of those systems respects our principle (I) from Section 1.4.2, since their axiomatizations include purely existential principles. An example is given by the
$\mathbf {PW}$
, none of those systems respects our principle (I) from Section 1.4.2, since their axiomatizations include purely existential principles. An example is given by the
![]() $\Sigma $
-reflection rule, which allows to infer
$\Sigma $
-reflection rule, which allows to infer
![]() $\exists a\psi ^{(a)}$
from
$\exists a\psi ^{(a)}$
from
![]() $\psi $
in case
$\psi $
in case
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma $
-formula (where
$\Sigma $
-formula (where
![]() $\psi ^{(a)}$
is obtained from
$\psi ^{(a)}$
is obtained from
![]() $\psi $
by restricting each quantifier in it to a).
$\psi $
by restricting each quantifier in it to a).
![]() $\mathbf {PS_iE}$
(
$\mathbf {PS_iE}$
(
![]() $i=0,1$
) violates Principle (II) (from Section 1.4.2) as well, since it includes an axiom that says that every set is enumerable. Another very significant point of difference is due to the fact (shown in [Reference Feferman, Scott and Jech18]) that
$i=0,1$
) violates Principle (II) (from Section 1.4.2) as well, since it includes an axiom that says that every set is enumerable. Another very significant point of difference is due to the fact (shown in [Reference Feferman, Scott and Jech18]) that
![]() $\mathbf {PS_1}$
and
$\mathbf {PS_1}$
and
![]() $\mathbf {PS_1E}$
has a minimum model consisting of all sets constructible before
$\mathbf {PS_1E}$
has a minimum model consisting of all sets constructible before
![]() $\Gamma _0$
. In contrast, the results of Section 7 imply than any transitive model of
$\Gamma _0$
. In contrast, the results of Section 7 imply than any transitive model of
![]() $\mathbf {PW}$
should contain
$\mathbf {PW}$
should contain
![]() $\Gamma _0$
. It follows that although the predicativity of the systems in [Reference Feferman, Scott and Jech18] is dubious, in some important sense they are all weaker than
$\Gamma _0$
. It follows that although the predicativity of the systems in [Reference Feferman, Scott and Jech18] is dubious, in some important sense they are all weaker than
![]() $\mathbf {PW}$
.Footnote
22
$\mathbf {PW}$
.Footnote
22
5 Some examples of the power of
 $\mathbf {PW}$
$\mathbf {PW}$
5.1 Abstraction terms and RST
Let
![]() $Fv(\varphi )=\{x,v_1 ,\ldots \!,\! v_n\}$
(
$Fv(\varphi )=\{x,v_1 ,\ldots \!,\! v_n\}$
(
![]() $n\geq 0$
), and suppose that
$n\geq 0$
), and suppose that
![]() $\varphi \succ \{x\}$
. Using [Comp], this entails
$\varphi \succ \{x\}$
. Using [Comp], this entails
Since the formula
![]() $\varphi ^\star :=\forall x(x\in v_0\leftrightarrow \varphi )$
is
$\varphi ^\star :=\forall x(x\in v_0\leftrightarrow \varphi )$
is
![]() $\Sigma $
,Footnote
23
an application of [OpI] yields
$\Sigma $
,Footnote
23
an application of [OpI] yields
Henceforth we shall write
![]() $\{x\mid \varphi (x,v_1 ,\ldots \!,\! v_n)\}$
instead of
$\{x\mid \varphi (x,v_1 ,\ldots \!,\! v_n)\}$
instead of
![]() $F_{\varphi ^\star }(v_1 ,\ldots \!,\! v_n)$
(where
$F_{\varphi ^\star }(v_1 ,\ldots \!,\! v_n)$
(where
![]() $\varphi ^\star $
is defined from
$\varphi ^\star $
is defined from
![]() $\varphi $
as above), and call this an abstraction term. Obviously,
$\varphi $
as above), and call this an abstraction term. Obviously,
![]() $\vdash _{\mathbf {PW}} \forall x(x\in \{x\mid \varphi \}\leftrightarrow \varphi )$
. It follows that
$\vdash _{\mathbf {PW}} \forall x(x\in \{x\mid \varphi \}\leftrightarrow \varphi )$
. It follows that
![]() $\mathbf {PW}$
is an extension of the theory
$\mathbf {PW}$
is an extension of the theory
![]() $\mathbf {RST}$
from [Reference Avron and Schindler5]. By the results of that paper, this implies that every rudimentary operation is definable in
$\mathbf {RST}$
from [Reference Avron and Schindler5]. By the results of that paper, this implies that every rudimentary operation is definable in
![]() $\mathbf {PW}$
. Here are some examples of terms available in
$\mathbf {PW}$
. Here are some examples of terms available in
![]() $\mathbf {RST}$
, and so in
$\mathbf {RST}$
, and so in
![]() $\mathbf {PW}$
:
$\mathbf {PW}$
:
-
•
 ${\emptyset }=_{Df}\{x\mid x\neq x\}.$
${\emptyset }=_{Df}\{x\mid x\neq x\}.$
-
•
 ${\{t_1 ,\ldots \!,\! t_n\}}=_{Df}\{x\mid x=t_1\vee \dots \vee x=t_n\}.$
${\{t_1 ,\ldots \!,\! t_n\}}=_{Df}\{x\mid x=t_1\vee \dots \vee x=t_n\}.$
-
•
 ${\langle t,s \rangle }=_{Df}\{\{t\},\{t,s\}\}.$
${\langle t,s \rangle }=_{Df}\{\{t\},\{t,s\}\}.$
-
•
 ${\{x\in t\mid \varphi \}}=_{Df}\{x\mid x\in t\wedge \varphi \}$
(provided
${\{x\in t\mid \varphi \}}=_{Df}\{x\mid x\in t\wedge \varphi \}$
(provided
 $\varphi \succ \emptyset $
and
$\varphi \succ \emptyset $
and
 $x\not \in Fv(t)$
).
$x\not \in Fv(t)$
). -
•
 ${\{t(x)\mid x\in s\}}=_{Df}\{y\mid \exists x.x\in s\wedge y=t\}.$
${\{t(x)\mid x\in s\}}=_{Df}\{y\mid \exists x.x\in s\wedge y=t\}.$
-
•
 ${\bigcup t}=_{Df}\{x\mid \exists y.y\in t\wedge x\in y\}.$
${\bigcup t}=_{Df}\{x\mid \exists y.y\in t\wedge x\in y\}.$
-
•
 ${s\times t}=_{Df}\{x\mid \exists a \exists b. a\in s \wedge b\in t \wedge x=\langle a,b \rangle \}.$
${s\times t}=_{Df}\{x\mid \exists a \exists b. a\in s \wedge b\in t \wedge x=\langle a,b \rangle \}.$
-
•
 ${\iota x\varphi }=_{Df}\bigcup \{x\mid \varphi \}$
(provided
${\iota x\varphi }=_{Df}\bigcup \{x\mid \varphi \}$
(provided
 $\varphi \succ \{x\}$
).
$\varphi \succ \{x\}$
). -
•
 ${\lambda x\in s.t}=_{Df} \{\langle x,t \rangle \mid x\in s\}.$
${\lambda x\in s.t}=_{Df} \{\langle x,t \rangle \mid x\in s\}.$
-
•
 ${f(x)}=_{Df} \iota y.\exists z\exists v(z\in f\wedge v\in z\wedge y\in v\wedge z=\langle x,y \rangle ).$
${f(x)}=_{Df} \iota y.\exists z\exists v(z\in f\wedge v\in z\wedge y\in v\wedge z=\langle x,y \rangle ).$
-
•
 $Dom(f)=\{x\in \bigcup f\mid \exists y\in \bigcup \bigcup f.\langle x,y \rangle \in f\}.$
$Dom(f)=\{x\in \bigcup f\mid \exists y\in \bigcup \bigcup f.\langle x,y \rangle \in f\}.$
-
•
 $Im(f)=\{x\in \bigcup f\mid \exists y\in \bigcup \bigcup f.\langle y,x \rangle \in f\}.$
$Im(f)=\{x\in \bigcup f\mid \exists y\in \bigcup \bigcup f.\langle y,x \rangle \in f\}.$
-
•
 $f\upharpoonright s=_{Df}\{\langle x,f(x) \rangle \mid x\in s\}$
(where x is new).
$f\upharpoonright s=_{Df}\{\langle x,f(x) \rangle \mid x\in s\}$
(where x is new).
Note 5.1. The definition of
![]() $\succ $
does not directly imply that
$\succ $
does not directly imply that
![]() $z=\langle x,y \rangle \succ \{y\}$
. Therefore we could not have defined above
$z=\langle x,y \rangle \succ \{y\}$
. Therefore we could not have defined above
![]() $f(x):=\iota y.\exists z(z\in f\wedge z=\langle x,y \rangle )$
. However, it is not difficult to construct a formula
$f(x):=\iota y.\exists z(z\in f\wedge z=\langle x,y \rangle )$
. However, it is not difficult to construct a formula
![]() $\psi (x,y,z)$
that is equivalent in
$\psi (x,y,z)$
that is equivalent in
![]() $\mathbf {PW}$
to
$\mathbf {PW}$
to
![]() $z=\langle x,y \rangle $
and
$z=\langle x,y \rangle $
and
![]() $\psi (x,y,z)\succ \{y\}$
, and even
$\psi (x,y,z)\succ \{y\}$
, and even
![]() $\psi (x,y,z)\succ \{x,y\}$
. (Implicitly, this is what is done above in the definition of
$\psi (x,y,z)\succ \{x,y\}$
. (Implicitly, this is what is done above in the definition of
![]() $f(x)$
.) Therefore from now in we assume that
$f(x)$
.) Therefore from now in we assume that
![]() $z=\langle x,y \rangle \succ \langle x,y \rangle $
. (In addition
$z=\langle x,y \rangle \succ \langle x,y \rangle $
. (In addition
![]() $z=\langle x,y \rangle \succ \{z\}$
too, of course.)
$z=\langle x,y \rangle \succ \{z\}$
too, of course.)
The following are examples of easy related theorems of RST:
-
•
 $\exists ! x\varphi (x)\to \forall x(\varphi (x)\leftrightarrow x=\iota x\varphi (x))$
(if
$\exists ! x\varphi (x)\to \forall x(\varphi (x)\leftrightarrow x=\iota x\varphi (x))$
(if
 $\varphi \succ \{x\}$
).
$\varphi \succ \{x\}$
). -
•
 $u\in s\to (\lambda x\in s.t)u=t\{u/x\}$
(if u is free for x in t).
$u\in s\to (\lambda x\in s.t)u=t\{u/x\}$
(if u is free for x in t). -
•
 $Fun(f)\to (\langle x,y \rangle \in f\leftrightarrow y=f(x))$
, where
$Fun(f)\to (\langle x,y \rangle \in f\leftrightarrow y=f(x))$
, where
 $Fun(f)$
is the following absolute formula (which says that f is a function):
$Fun(f)$
is the following absolute formula (which says that f is a function):  $$ \begin{align*}\forall z\in f\exists x\exists y(z=\langle x,y \rangle)\wedge\forall x\forall y_1\forall y_2( \langle x,y_1 \rangle\in f\wedge \langle x,y_2 \rangle\in f\to y_1=y_2).\end{align*} $$
$$ \begin{align*}\forall z\in f\exists x\exists y(z=\langle x,y \rangle)\wedge\forall x\forall y_1\forall y_2( \langle x,y_1 \rangle\in f\wedge \langle x,y_2 \rangle\in f\to y_1=y_2).\end{align*} $$
5.2 Explicit definitions and the extended [OpI]
5.2.1 Explicit definitions
Explicit definitions of operations are particularly simple case of applying [OpI]:
Proposition 5.2. Let t be a term of
![]() $\mathbf {PW}$
such that
$\mathbf {PW}$
such that
![]() $Fv(t)=\{v_1 ,\ldots \!,\! v_n\}$
. Then
$Fv(t)=\{v_1 ,\ldots \!,\! v_n\}$
. Then
![]() $\mathbf {PW}$
has an operation F such that
$\mathbf {PW}$
has an operation F such that
![]() $\vdash _{\mathbf {PW}}\forall v_1\cdots \forall v_n F(v_1 ,\ldots \!,\! v_n)=t$
.
$\vdash _{\mathbf {PW}}\forall v_1\cdots \forall v_n F(v_1 ,\ldots \!,\! v_n)=t$
.
Proof
![]() $F=F_\varphi $
, where
$F=F_\varphi $
, where
![]() $\varphi $
is
$\varphi $
is
![]() $v_0=t$
.
$v_0=t$
.
5.2.2 The extended [OpI]
The use of [OpI] can be made more effective with the help of the following proposition:
Proposition 5.3. For
![]() $1\leq i\leq k$
, let
$1\leq i\leq k$
, let
![]() $\varphi _i$
and
$\varphi _i$
and
![]() $\psi _i$
be formulas of
$\psi _i$
be formulas of
![]() $\mathbf {PW}$
such that
$\mathbf {PW}$
such that
![]() $\varphi _i\in \Sigma $
,
$\varphi _i\in \Sigma $
,
![]() $Fv(\varphi _i)=\{v_0,v_1,\ldots \!,v_n\}$
,
$Fv(\varphi _i)=\{v_0,v_1,\ldots \!,v_n\}$
,
![]() $\psi _i\succ \emptyset $
, and
$\psi _i\succ \emptyset $
, and
![]() $Fv(\psi _i)\subseteq \{v_1 ,\ldots \!,\! v_n\}$
. Suppose that for every
$Fv(\psi _i)\subseteq \{v_1 ,\ldots \!,\! v_n\}$
. Suppose that for every
![]() $1\leq i,j\leq k$
such that
$1\leq i,j\leq k$
such that
![]() $i\neq j$
we have that
$i\neq j$
we have that
![]() $\vdash _{\mathbf {PW}}\neg (\psi _i\wedge \psi _j)$
and that
$\vdash _{\mathbf {PW}}\neg (\psi _i\wedge \psi _j)$
and that
![]() $\vdash _{\mathbf {PW}}\forall v_1 ,\ldots \!,\! \forall v_n(\psi _i\to \exists !v_0\varphi _i)$
. Then
$\vdash _{\mathbf {PW}}\forall v_1 ,\ldots \!,\! \forall v_n(\psi _i\to \exists !v_0\varphi _i)$
. Then
![]() $\mathbf {PW}$
has an operation F such that for every
$\mathbf {PW}$
has an operation F such that for every
![]() $1\leq i\leq k$
:
$1\leq i\leq k$
:
![]() $\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n(\psi _i\to \varphi _i\{F(v_1 ,\ldots \!,\! v_n)/v_0\})$
.
$\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n(\psi _i\to \varphi _i\{F(v_1 ,\ldots \!,\! v_n)/v_0\})$
.
Proof
![]() $F\!=\!F_\theta $
, where
$F\!=\!F_\theta $
, where
![]() $\theta \!=\! (\psi _1\wedge \varphi _1)\!\vee \cdots \vee \!(\psi _k\wedge \varphi _k)\!\vee \! (\neg (\psi _1\wedge \dots \psi _k)\wedge v_0=0)$
.
$\theta \!=\! (\psi _1\wedge \varphi _1)\!\vee \cdots \vee \!(\psi _k\wedge \varphi _k)\!\vee \! (\neg (\psi _1\wedge \dots \psi _k)\wedge v_0=0)$
.
We shall call the principle stated in Proposition 5.3 the extended [OpI].
Example 5.4. Let
![]() $\varphi $
be the following
$\varphi $
be the following
![]() $\Sigma $
-formula (where we write
$\Sigma $
-formula (where we write
![]() $y,x,n$
instead of
$y,x,n$
instead of
![]() $v_0,v_1,v_2$
, respectively).
$v_0,v_1,v_2$
, respectively).
An induction on n shows that
![]() $\vdash _{\mathbf {PW}}\forall x\forall n(n\in \omega \to \exists !y\varphi )$
. Hence the extended [OpI] implies that
$\vdash _{\mathbf {PW}}\forall x\forall n(n\in \omega \to \exists !y\varphi )$
. Hence the extended [OpI] implies that
![]() $\vdash _{\mathbf {PW}}\forall x\forall n(n\in \omega \to \varphi \{H(x,n)/y\})$
for some operation H of
$\vdash _{\mathbf {PW}}\forall x\forall n(n\in \omega \to \varphi \{H(x,n)/y\})$
for some operation H of
![]() $\mathbf {PW}$
. Let
$\mathbf {PW}$
. Let
![]() $RTC(x)=\cup \{H(n,x)\mid n\in \omega \}$
. Then
$RTC(x)=\cup \{H(n,x)\mid n\in \omega \}$
. Then
![]() $RTC(x)$
represents in
$RTC(x)$
represents in
![]() $\mathbf {PW}$
the reflexive–transitive closure of x, and so
$\mathbf {PW}$
the reflexive–transitive closure of x, and so
![]() $TC(x)=RTC(x)-\{x\}$
represents the transitive closure of x. Hence the relation
$TC(x)=RTC(x)-\{x\}$
represents the transitive closure of x. Hence the relation
![]() $\in ^\star $
(the transitive closure of
$\in ^\star $
(the transitive closure of
![]() $\in $
) is definable in
$\in $
) is definable in
![]() $\mathbf {PW}$
by
$\mathbf {PW}$
by
![]() $y\in ^\star x=_{Df}y\in TC(x)$
.
$y\in ^\star x=_{Df}y\in TC(x)$
.
5.3 Transitive closures and PZF
Let
![]() $\psi $
be a formula of
$\psi $
be a formula of
![]() $\mathbf {PW}$
such that
$\mathbf {PW}$
such that
![]() $\{x,y\}\subseteq Fv(\psi )$
, and
$\{x,y\}\subseteq Fv(\psi )$
, and
![]() $\psi \succ \{y\}$
. Define
$\psi \succ \{y\}$
. Define
![]() $\varphi $
like in Example 5.4, replacing the conjunct
$\varphi $
like in Example 5.4, replacing the conjunct
![]() $\forall i\in n.f(i+1)=\bigcup f(i)$
by
$\forall i\in n.f(i+1)=\bigcup f(i)$
by
![]() $\forall i\in n.f(i+1)=\{y\mid \exists z\in f(i).\psi \{z/x\}\}$
. Following exactly the same procedure as in Example 5.4, we construct in
$\forall i\in n.f(i+1)=\{y\mid \exists z\in f(i).\psi \{z/x\}\}$
. Following exactly the same procedure as in Example 5.4, we construct in
![]() $\mathbf {PW}$
an operation
$\mathbf {PW}$
an operation
![]() $TC_\psi $
such that
$TC_\psi $
such that
![]() $TC_\psi (x,y):=y\in TC_\psi (x)$
is true iff there is a finite
$TC_\psi (x,y):=y\in TC_\psi (x)$
is true iff there is a finite
![]() $\psi $
-chain that connects y to x. Hence this formula is semantically equivalent to the formula
$\psi $
-chain that connects y to x. Hence this formula is semantically equivalent to the formula
![]() $(TC_{x,y}\psi )(x,y)$
of PZF. Moreover, like the latter,
$(TC_{x,y}\psi )(x,y)$
of PZF. Moreover, like the latter,
![]() $TC_\psi (x,y)\succ \{y\}$
. It is also easy to prove in
$TC_\psi (x,y)\succ \{y\}$
. It is also easy to prove in
![]() $\mathbf {PW}$
that
$\mathbf {PW}$
that
![]() $TC_\psi (x,y)$
has all the properties that
$TC_\psi (x,y)$
has all the properties that
![]() $(TC_{x,y}\psi )(x,y)$
has in PZF according to Section 3.3 of [Reference Avron and Schindler5]. It follows that
$(TC_{x,y}\psi )(x,y)$
has in PZF according to Section 3.3 of [Reference Avron and Schindler5]. It follows that
![]() $\mathbf {PW}$
contains PZF.
$\mathbf {PW}$
contains PZF.
5.4 The use of
 $\Delta $
-formulas
$\Delta $
-formulas
Definition 5.5. A formula
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Delta $
-formula if both
$\Delta $
-formula if both
![]() $\varphi $
and
$\varphi $
and
![]() $\neg \varphi $
are equivalent in
$\neg \varphi $
are equivalent in
![]() $\mathbf {PW}$
to
$\mathbf {PW}$
to
![]() $\Sigma $
-formulas.
$\Sigma $
-formulas.
Proposition 5.6. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Delta $
-formula,
$\Delta $
-formula,
![]() $Fv(\varphi )=\{v_1 ,\ldots \!,\! v_n\}$
. Then
$Fv(\varphi )=\{v_1 ,\ldots \!,\! v_n\}$
. Then
![]() $\mathbf {PW}$
has an n-ary predicate
$\mathbf {PW}$
has an n-ary predicate
![]() $R_{\varphi }$
such that
$R_{\varphi }$
such that
![]() $\vdash _{\mathbf {PW}} R_{\varphi }(v_1 ,\ldots \!,\! v_n)\leftrightarrow \varphi $
.
$\vdash _{\mathbf {PW}} R_{\varphi }(v_1 ,\ldots \!,\! v_n)\leftrightarrow \varphi $
.
Proof Let
![]() $\psi :=(\varphi \wedge v_0=1)\vee (\neg \varphi \wedge v_0=0)$
. Obviously,
$\psi :=(\varphi \wedge v_0=1)\vee (\neg \varphi \wedge v_0=0)$
. Obviously,
![]() $\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n\exists !v_0\psi $
, and
$\vdash _{\mathbf {PW}}\forall v_1\dots \forall v_n\exists !v_0\psi $
, and
![]() $\psi $
is equivalent in
$\psi $
is equivalent in
![]() $\mathbf {PW}$
to a
$\mathbf {PW}$
to a
![]() $\Delta $
-formula
$\Delta $
-formula
![]() $\psi ^\star $
. Therefore by [OpI] we get
$\psi ^\star $
. Therefore by [OpI] we get
It follows that
![]() $\vdash _{\mathbf {PW}}\varphi \leftrightarrow F_{\psi ^\star }(v_1 ,\ldots \!,\! v_n)=1$
. Let
$\vdash _{\mathbf {PW}}\varphi \leftrightarrow F_{\psi ^\star }(v_1 ,\ldots \!,\! v_n)=1$
. Let
![]() $\varphi ^\star :=F_{\psi ^\star }(v_1 ,\ldots \!,\! v_n)=1$
. Then
$\varphi ^\star :=F_{\psi ^\star }(v_1 ,\ldots \!,\! v_n)=1$
. Then
![]() $\varphi ^\star $
is absolute. Hence we may apply [PrI] to it. Take
$\varphi ^\star $
is absolute. Hence we may apply [PrI] to it. Take
![]() $R_{\varphi }$
to be
$R_{\varphi }$
to be
![]() $P_{\varphi ^\star }$
.
$P_{\varphi ^\star }$
.
Corollary 5.7.
![]() $\mathbf {PW}$
has a predicate
$\mathbf {PW}$
has a predicate
![]() $Tr$
which defines in it truth in
$Tr$
which defines in it truth in
![]() $\mathcal {N}$
of formulas in the first-order language of
$\mathcal {N}$
of formulas in the first-order language of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
Proof It is well-known that truth in
![]() $\mathcal {N}$
for that language is definable by a
$\mathcal {N}$
for that language is definable by a
![]() $\Delta $
-formula, and it is not difficult to see that the main properties of truth are derivable in
$\Delta $
-formula, and it is not difficult to see that the main properties of truth are derivable in
![]() $\mathbf {PW}$
for the corresponding predicate that Proposition 5.6 provides.
$\mathbf {PW}$
for the corresponding predicate that Proposition 5.6 provides.
Corollary 5.8. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Delta $
-formula,
$\Delta $
-formula,
![]() $Fv(\varphi )=\{v_1 ,\ldots \!,\! v_n\}$
. Then:
$Fv(\varphi )=\{v_1 ,\ldots \!,\! v_n\}$
. Then:
Note 5.9. The stronger form of [PrI] given by Proposition 5.6 appears as an admissible procedure in [Reference Feferman, Scott and Jech18]. (see (ii) on page 18 there). However, its direct use for getting new instances of nonlogical schemas of the theory
![]() $\mathbf {PS}_1$
considered there is explicitly forbidden—in sharp contrast to its use here. Our Corollary 5.8 provides what is called in [Reference Feferman16] the ‘predicative separation rule’. Both the procedure and the rule are obvious counterparts of [HCR] (also called [
$\mathbf {PS}_1$
considered there is explicitly forbidden—in sharp contrast to its use here. Our Corollary 5.8 provides what is called in [Reference Feferman16] the ‘predicative separation rule’. Both the procedure and the rule are obvious counterparts of [HCR] (also called [
![]() $\Delta ^1_1$
-CR] in, e.g., [Reference Feferman and Shapiro24])—the hyperarithmetic comprehension rule. This rule is used in [Reference Feferman15] as the basis of the progression of theories
$\Delta ^1_1$
-CR] in, e.g., [Reference Feferman and Shapiro24])—the hyperarithmetic comprehension rule. This rule is used in [Reference Feferman15] as the basis of the progression of theories
![]() $\mathbf {HC}_{\alpha }$
, as well as in the single second-order theory IR. According to [Reference Feferman15], the latter proves exactly the second-order arithmetic formulas that can be proved by predicative means according to the
$\mathbf {HC}_{\alpha }$
, as well as in the single second-order theory IR. According to [Reference Feferman15], the latter proves exactly the second-order arithmetic formulas that can be proved by predicative means according to the
![]() $\Gamma _0$
-thesis.
$\Gamma _0$
-thesis.
5.5 Predicative set-theoretic recursion
Theorem 5.10. Let F be an (
![]() $n+2$
)-ary operation of
$n+2$
)-ary operation of
![]() $\mathbf {PW}$
. Then
$\mathbf {PW}$
. Then
![]() $\mathbf {PW}$
has an (
$\mathbf {PW}$
has an (
![]() $n+1$
)-ary operation G such that
$n+1$
)-ary operation G such that
(where by
![]() $G\!\upharpoonright \!y$
we mean the function
$G\!\upharpoonright \!y$
we mean the function
![]() $\lambda u\in y.G(z_1 ,\ldots \!,\! z_n,u)$
).
$\lambda u\in y.G(z_1 ,\ldots \!,\! z_n,u)$
).
Proof For simplicity of the presentation, we prove the case
![]() $n=0$
. We freely use (here and later) facts about provability in
$n=0$
. We freely use (here and later) facts about provability in
![]() $\mathbf {PW}$
that can easily be seen.
$\mathbf {PW}$
that can easily be seen.
Define a formula
![]() $\varphi $
such that
$\varphi $
such that
![]() $Fv(\varphi )=\{x,f\}$
by
$Fv(\varphi )=\{x,f\}$
by
Next we show that
![]() $\varphi $
has the following properties.
$\varphi $
has the following properties.
-
1.
 $\varphi $
is absolute.This easily follows from Example 5.4.
$\varphi $
is absolute.This easily follows from Example 5.4. -
2.
 $\vdash _{\mathbf {PW}}\varphi (x,f)\wedge z\in RTC(x)\to \varphi (z,f\!\upharpoonright \!RTC(z)).$
$\vdash _{\mathbf {PW}}\varphi (x,f)\wedge z\in RTC(x)\to \varphi (z,f\!\upharpoonright \!RTC(z)).$
This follows from
 $\vdash _{\mathbf {PW}} z\in x\to RTC(z)\subseteq RTC(x)$
and
$\vdash _{\mathbf {PW}} z\in x\to RTC(z)\subseteq RTC(x)$
and
 $\varphi $
’s definition.
$\varphi $
’s definition. -
3.
 $\vdash _{\mathbf {PW}}\varphi (x,f_1)\wedge \varphi (x,f_2)\to f_1=f_2.$
$\vdash _{\mathbf {PW}}\varphi (x,f_1)\wedge \varphi (x,f_2)\to f_1=f_2.$
The proof is by
 $\in $
-induction on x, using the previous item and the fact that
$\in $
-induction on x, using the previous item and the fact that
 $\vdash _{\mathbf {PW}} RTC(x)=\{x\}\cup \bigcup \{RTC(z)\mid z\in x\}$
.
$\vdash _{\mathbf {PW}} RTC(x)=\{x\}\cup \bigcup \{RTC(z)\mid z\in x\}$
. -
4.
 $\vdash _{\mathbf {PW}}\varphi (x_1,f_1)\wedge \varphi (x_2,f_2)\wedge z\in RTC(x_1)\cap RTC(x_2) \to f_1(z)=f_2(z).$
$\vdash _{\mathbf {PW}}\varphi (x_1,f_1)\wedge \varphi (x_2,f_2)\wedge z\in RTC(x_1)\cap RTC(x_2) \to f_1(z)=f_2(z).$
This follows from the previous two items and the definition of
 $\varphi $
.
$\varphi $
. -
5.
 $\vdash _{\mathbf {PW}}\forall x\exists f\varphi (x,f).$
$\vdash _{\mathbf {PW}}\forall x\exists f\varphi (x,f).$
The proof is by an
 $\in $
-induction (in
$\in $
-induction (in
 $\mathbf {PW}$
) on x. So assume (in
$\mathbf {PW}$
) on x. So assume (in
 $\mathbf {PW}$
) that
$\mathbf {PW}$
) that
 $\forall z\in TC(x) \exists g\varphi (z,g)$
. Using an application of [Unif] (which is justified by items 1 and 3), it follows from this assumption that there is a function g such that
$\forall z\in TC(x) \exists g\varphi (z,g)$
. Using an application of [Unif] (which is justified by items 1 and 3), it follows from this assumption that there is a function g such that
 $Dom(g)=TC(x)$
and
$Dom(g)=TC(x)$
and
 $\varphi (z,g(z))$
holds for every
$\varphi (z,g(z))$
holds for every
 $z\in TC(x)$
. Let
$z\in TC(x)$
. Let
 $f^\star =\bigcup \{g(z)\mid z\in TC(x)\}$
. From item 4 it follows that
$f^\star =\bigcup \{g(z)\mid z\in TC(x)\}$
. From item 4 it follows that
 $f^\star $
is a function whose domain is
$f^\star $
is a function whose domain is
 $TC(x)$
. Let
$TC(x)$
. Let
 $f=f^\star \cup \{\langle x,F(x,f^\star ) \rangle \}$
. It is straightforward to verify that
$f=f^\star \cup \{\langle x,F(x,f^\star ) \rangle \}$
. It is straightforward to verify that
 $\varphi (x,f)$
.
$\varphi (x,f)$
.
Define
![]() $\psi (x,y)=\exists f.\varphi (x,f)\wedge f(x)=y$
. From items 3 and 5 it follows that
$\psi (x,y)=\exists f.\varphi (x,f)\wedge f(x)=y$
. From items 3 and 5 it follows that
![]() $\vdash _{\mathbf {PW}}\forall x\exists !y\psi (x,y)$
, while item 1 implies that
$\vdash _{\mathbf {PW}}\forall x\exists !y\psi (x,y)$
, while item 1 implies that
![]() $\psi $
is a
$\psi $
is a
![]() $\Sigma $
-formula. Therefore by applying [OpI] we get an operation G such that
$\Sigma $
-formula. Therefore by applying [OpI] we get an operation G such that
![]() $\vdash _{\mathbf {PW}}\psi \{G(x)/y\}$
. Obviously, G has the required property.
$\vdash _{\mathbf {PW}}\psi \{G(x)/y\}$
. Obviously, G has the required property.
Example 5.11. From Theorem 5.10 it follows that
![]() $\mathbf {PW}$
has a unary operation
$\mathbf {PW}$
has a unary operation
![]() $rank$
such that
$rank$
such that
![]() $\vdash _{\mathbf {PW}} rank(x)=\bigcup \{S(rank(y))\mid y\in x\}$
. Obviously, platonists assign to any set which predicativists construct the same rank as the predicativists do.
$\vdash _{\mathbf {PW}} rank(x)=\bigcup \{S(rank(y))\mid y\in x\}$
. Obviously, platonists assign to any set which predicativists construct the same rank as the predicativists do.
6 Ordinals in
 $\mathbf {PW}$
$\mathbf {PW}$
The notion of an ordinal as a type of some well-order R is totally impredicative. Therefore like in ZF (and unlike Feferman or Schütte), we identify here the notion of an ordinal with that of a von Neumann’s ordinal.
6.1 Basic theory of ordinals
Definition 6.1.
-
•
 $Tra(x)\ :=\ \forall y\in x\forall z\in y. z\in x$
(x is transitive).
$Tra(x)\ :=\ \forall y\in x\forall z\in y. z\in x$
(x is transitive). -
•
 $Lin(x)\ :=\ \forall y\in x\forall z\in x. y\in z\vee y=z\vee z\in y$
(x is linear).
$Lin(x)\ :=\ \forall y\in x\forall z\in x. y\in z\vee y=z\vee z\in y$
(x is linear). -
•
 $On(x)\ :=\ Tra(x)\wedge Lin(x)$
(x is an ordinal).
$On(x)\ :=\ Tra(x)\wedge Lin(x)$
(x is an ordinal).
As usual, we use small Greek letters to vary over ordinals (writing, e.g.,
![]() $\exists \alpha \varphi $
instead of
$\exists \alpha \varphi $
instead of
![]() $\exists x(On (x) \wedge \varphi )$
and
$\exists x(On (x) \wedge \varphi )$
and
![]() $\forall \alpha \varphi $
instead of
$\forall \alpha \varphi $
instead of
![]() $\forall x(On(x)\to \varphi )$
). We shall also frequently write
$\forall x(On(x)\to \varphi )$
). We shall also frequently write
![]() $\alpha <\beta $
instead of
$\alpha <\beta $
instead of
![]() $\alpha \in \beta $
and
$\alpha \in \beta $
and
![]() $\alpha \leq \beta $
instead of
$\alpha \leq \beta $
instead of
![]() $\alpha \in \beta \vee \alpha =\beta $
.
$\alpha \in \beta \vee \alpha =\beta $
.
Proposition 6.2. The following are provable already in
![]() $\mathbf {VBS}$
:
$\mathbf {VBS}$
:
-
1.
 $On(\alpha )\wedge \beta \in \alpha \to On(\beta ).$
$On(\alpha )\wedge \beta \in \alpha \to On(\beta ).$
-
2.
 $On(\emptyset ).$
$On(\emptyset ).$
-
3.
 $On(\alpha )\leftrightarrow On(S(\alpha )).$
$On(\alpha )\leftrightarrow On(S(\alpha )).$
-
4.
 $\alpha \leq \beta \leftrightarrow \alpha \subseteq \beta .$
$\alpha \leq \beta \leftrightarrow \alpha \subseteq \beta .$
-
5.
 $\alpha \leq \beta \leftrightarrow \alpha \in S(\beta ).$
$\alpha \leq \beta \leftrightarrow \alpha \in S(\beta ).$
-
6.
 $\alpha =\emptyset \vee \emptyset \in \alpha $
.
$\alpha =\emptyset \vee \emptyset \in \alpha $
. -
7.
 $\beta \in \alpha \to (\alpha =S(\beta )\vee S(\beta )\in \alpha )$
.
$\beta \in \alpha \to (\alpha =S(\beta )\vee S(\beta )\in \alpha )$
. -
8.
 $\beta \in \alpha \vee \alpha =\beta \vee \alpha \in \beta .$
$\beta \in \alpha \vee \alpha =\beta \vee \alpha \in \beta .$
-
9. Every transitive set of ordinals is an ordinal.
-
10. Every set A of ordinals has a supremum
 $sup\;\!A$
.
$sup\;\!A$
. -
11. If
 $\alpha \neq 0$
then
$\alpha \neq 0$
then
 $\alpha =sup\;\!\alpha \vee \alpha =S(sup\;\!\alpha )$
(and not both). In the first case
$\alpha =sup\;\!\alpha \vee \alpha =S(sup\;\!\alpha )$
(and not both). In the first case
 $\alpha $
is called a limit ordinal, in the second—a successor.
$\alpha $
is called a limit ordinal, in the second—a successor. -
12. Every non-empty set A of ordinals has a minimal element
 $min\;\!A$
.
$min\;\!A$
.
Proof All the proofs are standard, and are left for the reader. We just note that none of the proofs requires the full power of the
![]() $\in $
-induction schema of
$\in $
-induction schema of
![]() $\mathbf {VBS}$
;
$\mathbf {VBS}$
;
![]() $\in $
-induction limited to absolute formulas suffices. (The latter principle is equivalent to the foundation axiom of ZF.)
$\in $
-induction limited to absolute formulas suffices. (The latter principle is equivalent to the foundation axiom of ZF.)
From now on, we leave to the readers most of the proofs of claims about provability in
![]() $\mathbf {PW}$
in case the proofs in
$\mathbf {PW}$
in case the proofs in
![]() $\mathbf {PW}$
are practically just the standard ones, and their availability in
$\mathbf {PW}$
are practically just the standard ones, and their availability in
![]() $\mathbf {PW}$
can easily be checked. (This does not include, of course, any proof which makes use of [PrI], [OpI], or [Unif].)
$\mathbf {PW}$
can easily be checked. (This does not include, of course, any proof which makes use of [PrI], [OpI], or [Unif].)
Proposition 6.3. The principle of transfinite induction on ordinals is available in
![]() ${\mathbf {PW}}$
:
${\mathbf {PW}}$
:
![]() $\vdash _{\mathbf {PW}}\forall \alpha (\forall \beta <\alpha \varphi (\beta )\to \varphi (\alpha ))\to \forall \alpha \varphi (\alpha )$
.
$\vdash _{\mathbf {PW}}\forall \alpha (\forall \beta <\alpha \varphi (\beta )\to \varphi (\alpha ))\to \forall \alpha \varphi (\alpha )$
.
6.2 Operations on ordinals
Theorem 6.4. Let F be an (
![]() $n+2$
)-ary operation in
$n+2$
)-ary operation in
![]() $\mathbf {PW}$
. Then
$\mathbf {PW}$
. Then
![]() $\mathbf {PW}$
has an (
$\mathbf {PW}$
has an (
![]() $n+1$
)-ary operation G such that
$n+1$
)-ary operation G such that
Proof Immediate from Theorem 5.10, since
![]() $\vdash _{\mathbf {PW}} On(\alpha )\to TC(\alpha )=\alpha $
.
$\vdash _{\mathbf {PW}} On(\alpha )\to TC(\alpha )=\alpha $
.
Once we have the ability to use transfinite recursion on ordinals, we can introduce the standard binary operations of addition (
![]() $\alpha +\beta $
), multiplication (
$\alpha +\beta $
), multiplication (
![]() $\alpha \times \beta $
) and exponentiation (
$\alpha \times \beta $
) and exponentiation (
![]() $\alpha ^\beta $
) in the usual way, and prove their main properties using transfinite induction. One particularly important such property is given in the next definition and proposition.
$\alpha ^\beta $
) in the usual way, and prove their main properties using transfinite induction. One particularly important such property is given in the next definition and proposition.
Definition 6.5. An ordinal
![]() $\alpha $
is additive principal if
$\alpha $
is additive principal if
![]() $\xi +\alpha =\alpha $
for every
$\xi +\alpha =\alpha $
for every
![]() $\xi <\alpha $
.
$\xi <\alpha $
.
Proposition 6.6.
![]() $\vdash _{\mathbf {PW}}\alpha $
is additive principal iff
$\vdash _{\mathbf {PW}}\alpha $
is additive principal iff
![]() $\alpha =\omega ^\xi $
for some
$\alpha =\omega ^\xi $
for some
![]() $\xi <\alpha $
.
$\xi <\alpha $
.
In the sequel we shall also need the following theorem about
![]() $\omega $
-sequences.
$\omega $
-sequences.
Theorem 6.7. Suppose that
![]() $(*)\ \vdash _{\mathbf {PW}} \psi (\alpha ,\beta _1)\wedge \psi (\alpha ,\beta _2)\to \beta _1=\beta _2$
, where
$(*)\ \vdash _{\mathbf {PW}} \psi (\alpha ,\beta _1)\wedge \psi (\alpha ,\beta _2)\to \beta _1=\beta _2$
, where
![]() $\psi (\alpha ,\beta )$
is a
$\psi (\alpha ,\beta )$
is a
![]() $\Sigma $
-formula. Then the following is a theorem of
$\Sigma $
-formula. Then the following is a theorem of
![]() $\mathbf {PW}$
:
$\mathbf {PW}$
:
Proof The proof of the uniqueness of f is standard, and is left to the reader. For the existence of f, let
![]() $\theta (\gamma ,n,h)$
be the following
$\theta (\gamma ,n,h)$
be the following
![]() $\Sigma $
-formula:
$\Sigma $
-formula:
Using
![]() $(*)$
, an easy induction on k shows that
$(*)$
, an easy induction on k shows that
Hence
![]() $(**)\ \vdash _{\mathbf {PW}} \theta (\gamma ,n,h_1)\wedge \theta (\gamma ,n,h_2) \to h_1=h_2$
.
$(**)\ \vdash _{\mathbf {PW}} \theta (\gamma ,n,h_1)\wedge \theta (\gamma ,n,h_2) \to h_1=h_2$
.
Since
![]() $\theta $
is a
$\theta $
is a
![]() $\Sigma $
-formula, it follows from
$\Sigma $
-formula, it follows from
![]() $(**)$
by [Unif] that
$(**)$
by [Unif] that
On the other hand, it is straightforward to prove in
![]() ${\mathbf {PW}}$
by induction on n that
${\mathbf {PW}}$
by induction on n that
![]() $\forall \alpha \exists \beta \psi (\alpha ,\beta )\to \forall n\in \omega \exists h\;\theta (\gamma ,n,h)$
. Given
$\forall \alpha \exists \beta \psi (\alpha ,\beta )\to \forall n\in \omega \exists h\;\theta (\gamma ,n,h)$
. Given
![]() $\gamma $
, the assumption that
$\gamma $
, the assumption that
![]() $\forall \alpha \exists \beta \psi (\alpha ,\beta )$
implies therefore in
$\forall \alpha \exists \beta \psi (\alpha ,\beta )$
implies therefore in
![]() $\mathbf {PW}$
that there exists a function g such that
$\mathbf {PW}$
that there exists a function g such that
![]() $Dom(g)=\omega $
and
$Dom(g)=\omega $
and
![]() $\theta (\gamma ,n,g(n))$
holds for every
$\theta (\gamma ,n,g(n))$
holds for every
![]() $n\in \omega $
. It is easy now to verify (assuming
$n\in \omega $
. It is easy now to verify (assuming
![]() $\forall \alpha \exists \beta \psi (\alpha ,\beta )$
) that
$\forall \alpha \exists \beta \psi (\alpha ,\beta )$
) that
![]() $\lambda n\in w.g(n)(n)$
has the required properties.
$\lambda n\in w.g(n)(n)$
has the required properties.
6.3 Ordering functions
Definition 6.8. A function f such that
![]() $Dom(f)$
and
$Dom(f)$
and
![]() $Im(f)$
consist of ordinals is strictly monotonic if
$Im(f)$
consist of ordinals is strictly monotonic if
![]() $f(\beta )< f(\gamma )$
whenever
$f(\beta )< f(\gamma )$
whenever
![]() $\beta <\gamma $
(
$\beta <\gamma $
(
![]() $\beta ,\gamma \in Dom(f)$
).
$\beta ,\gamma \in Dom(f)$
).
Proposition 6.9.
![]() $\mathbf {PW}$
proves that if f is a strictly monotonic function such that
$\mathbf {PW}$
proves that if f is a strictly monotonic function such that
![]() $ Dom(f)$
is an ordinal, then
$ Dom(f)$
is an ordinal, then
![]() $\alpha \leq f(\alpha )$
for every
$\alpha \leq f(\alpha )$
for every
![]() $\alpha \in Dom(f)$
.
$\alpha \in Dom(f)$
.
Proof By transfinite induction on
![]() $\alpha $
.
$\alpha $
.
Notation.
![]() $f[X]=_{Df}\{f(x)\mid x\in X\}$
.
$f[X]=_{Df}\{f(x)\mid x\in X\}$
.
Definition 6.10. A function f is an ordering function of a set B of ordinals, (in symbols:
![]() $Ord(f,B)$
) if:
$Ord(f,B)$
) if:
-
•
 $Dom(f)$
is an ordinal.
$Dom(f)$
is an ordinal. -
•
 $Im(f)=B$
.
$Im(f)=B$
. -
• f is strictly monotonic.
Proposition 6.11.
![]() $\mathbf {PW}$
proves that every set B of ordinals has a unique ordering function f.
$\mathbf {PW}$
proves that every set B of ordinals has a unique ordering function f.
Proof The proof of uniqueness is standard, and is left for the reader.
To prove the existence of f, we first introduce the following abbreviations:
 $$ \begin{align*}&\psi:= (\xi\in X\vee \xi>sup\;\!X)\wedge\xi\not\in Im(g)\wedge \forall\beta\\&\quad<\xi((\beta\in X\vee \beta>sup\;\!X)\to \beta\in Im(g)).\end{align*} $$
$$ \begin{align*}&\psi:= (\xi\in X\vee \xi>sup\;\!X)\wedge\xi\not\in Im(g)\wedge \forall\beta\\&\quad<\xi((\beta\in X\vee \beta>sup\;\!X)\to \beta\in Im(g)).\end{align*} $$
It is easy to see that
Using items 10 and 12 of Proposition 6.2, this implies
Since
![]() $\varphi $
is absolute, and
$\varphi $
is absolute, and
![]() $\psi $
is in
$\psi $
is in
![]() $\Sigma $
(and even absolute), an application of the extended [OpI] (Section 5.2.2) provides therefore an operation F such that
$\Sigma $
(and even absolute), an application of the extended [OpI] (Section 5.2.2) provides therefore an operation F such that
It easily follows from that by Theorem 6.4 that
![]() $\mathbf {PW}$
has an operation G such that
$\mathbf {PW}$
has an operation G such that
Suppose now that B is a set of ordinals. Then it follows from the last two theorems of
![]() $\mathbf {PW}$
shown above that
$\mathbf {PW}$
shown above that
![]() $\forall \xi \psi (B,\lambda \tau \in \xi .G(B,\tau ), G(B,\xi ))$
. It is straightforward to show that for every ordinal
$\forall \xi \psi (B,\lambda \tau \in \xi .G(B,\tau ), G(B,\xi ))$
. It is straightforward to show that for every ordinal
![]() $\xi $
,
$\xi $
,
![]() $\lambda \tau \in \xi .G(B,\tau )$
is strictly monotonic. It follows by Proposition 6.9 that
$\lambda \tau \in \xi .G(B,\tau )$
is strictly monotonic. It follows by Proposition 6.9 that
![]() $G(B,S(supB))\geq S(supB)$
, and so
$G(B,S(supB))\geq S(supB)$
, and so
![]() $G(B,S(supB)\not \in B$
. Let
$G(B,S(supB)\not \in B$
. Let
![]() $\beta $
be the minimal ordinal such that
$\beta $
be the minimal ordinal such that
![]() $G(B,\beta )\not \in B$
. It is not difficult to see that
$G(B,\beta )\not \in B$
. It is not difficult to see that
![]() $\lambda \tau \in \beta .G(X,\tau )$
is an ordering function of B.
$\lambda \tau \in \beta .G(X,\tau )$
is an ordering function of B.
7 The operations
 $\phi $
and
$\phi $
and
 $\Gamma $
$\Gamma $
The main problem dealt with in this section is to define the operations
![]() $\phi $
and
$\phi $
and
![]() $\Gamma $
which are needed for the standard definition of the ordinal
$\Gamma $
which are needed for the standard definition of the ordinal
![]() $\Gamma _0$
(i.e.,
$\Gamma _0$
(i.e.,
![]() $\Gamma (0)$
). That this is possible is not at all obvious. Let us explain the difficulty. Recall (see, e.g., [Reference Schütte43]) that the binary operation
$\Gamma (0)$
). That this is possible is not at all obvious. Let us explain the difficulty. Recall (see, e.g., [Reference Schütte43]) that the binary operation
![]() $\phi $
is defined by
$\phi $
is defined by
![]() $\phi (\alpha ,\beta )=\phi _{\alpha }(\beta )$
, where
$\phi (\alpha ,\beta )=\phi _{\alpha }(\beta )$
, where
![]() $\phi _0(\beta )=\omega ^\beta $
, and for
$\phi _0(\beta )=\omega ^\beta $
, and for
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\phi _{\alpha }(\beta )$
is the
$\phi _{\alpha }(\beta )$
is the
![]() $\beta $
th ordinal
$\beta $
th ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $\phi _{\xi }(\gamma )=\gamma $
for every
$\phi _{\xi }(\gamma )=\gamma $
for every
![]() $\xi <\alpha $
. (The unary operation
$\xi <\alpha $
. (The unary operation
![]() $\Gamma $
on ordinals is then defined by letting
$\Gamma $
on ordinals is then defined by letting
![]() $\Gamma (\beta )$
be the
$\Gamma (\beta )$
be the
![]() $\beta $
th ordinal
$\beta $
th ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $\phi (\gamma ,0)=\gamma $
. In particular,
$\phi (\gamma ,0)=\gamma $
. In particular,
![]() $\Gamma _0$
is the first fixed-point of the operation
$\Gamma _0$
is the first fixed-point of the operation
![]() $\lambda \alpha .\phi (\alpha ,0)$
.) Hence
$\lambda \alpha .\phi (\alpha ,0)$
.) Hence
![]() $\phi $
is obtained as the unification of the class
$\phi $
is obtained as the unification of the class
![]() $[\phi _{\alpha }\mid On(\alpha )]$
. Unfortunately, in
$[\phi _{\alpha }\mid On(\alpha )]$
. Unfortunately, in
![]() $\mathbf {PW}$
we can unify only a set of functions, not a set of operations, and certainly not a class of operations. In fact, we cannot even define sets of operations in
$\mathbf {PW}$
we can unify only a set of functions, not a set of operations, and certainly not a class of operations. In fact, we cannot even define sets of operations in
![]() $\mathbf {PW}$
, since operations are not objects of it. Our problem is therefore to find some set of functions that can replace the class of operations
$\mathbf {PW}$
, since operations are not objects of it. Our problem is therefore to find some set of functions that can replace the class of operations
![]() $[\phi _{\alpha }\mid On(\alpha )]$
in the definition of
$[\phi _{\alpha }\mid On(\alpha )]$
in the definition of
![]() $\phi (\alpha ,\beta )$
.
$\phi (\alpha ,\beta )$
.
Note 7.1. The problem does not arise, e.g., in the development of
![]() $\phi $
and
$\phi $
and
![]() $\Gamma $
in §13 of [Reference Schütte43], since the existence of the set O of all countable ordinals is assumed there. This assumption makes it possible to take each
$\Gamma $
in §13 of [Reference Schütte43], since the existence of the set O of all countable ordinals is assumed there. This assumption makes it possible to take each
![]() $\phi _{\alpha }$
(where
$\phi _{\alpha }$
(where
![]() $\alpha \in O$
) as a function from O to O. Doing the same is of course impossible in the framework of
$\alpha \in O$
) as a function from O to O. Doing the same is of course impossible in the framework of
![]() $\mathbf {PW}$
, since O is not available there.
$\mathbf {PW}$
, since O is not available there.
7.1 The binary operation
 $\phi $
$\phi $
Definition 7.2. The absolute formula
![]() $\psi _\phi (\delta ,\alpha ,f)$
is the conjunction of the following absolute formulas:
$\psi _\phi (\delta ,\alpha ,f)$
is the conjunction of the following absolute formulas:
-
1.
 $On(\alpha )\wedge On(\delta ).$
$On(\alpha )\wedge On(\delta ).$
-
2.
 $Fun(f)\wedge Dom(f)=\alpha .$
$Fun(f)\wedge Dom(f)=\alpha .$
-
3.
 $\forall \xi \kern1.2pt{\in}\kern1.2pt \alpha (Fun(f(\xi ))\kern1.2pt{\wedge}\kern1.2pt On(Dom(f(\xi )))\kern1.2pt{\wedge}\kern1.2pt \forall \tau \kern1.2pt{\in}\kern1.2pt Dom(f(\xi )) On(f(\xi )(\tau ))).$
$\forall \xi \kern1.2pt{\in}\kern1.2pt \alpha (Fun(f(\xi ))\kern1.2pt{\wedge}\kern1.2pt On(Dom(f(\xi )))\kern1.2pt{\wedge}\kern1.2pt \forall \tau \kern1.2pt{\in}\kern1.2pt Dom(f(\xi )) On(f(\xi )(\tau ))).$
-
4.
 $\alpha>0\to (Dom(f(0))=\delta \wedge \forall \tau <\delta (f(0)(\tau )=\omega ^\tau )).$
$\alpha>0\to (Dom(f(0))=\delta \wedge \forall \tau <\delta (f(0)(\tau )=\omega ^\tau )).$
-
5.
 $\forall \xi (0<\xi <\alpha \to Ord(f(\xi ),\{\tau \in \delta \mid \forall \eta <\xi (\tau \in Dom(f(\eta ))\wedge f(\eta )(\tau )=\tau )\}).$
$\forall \xi (0<\xi <\alpha \to Ord(f(\xi ),\{\tau \in \delta \mid \forall \eta <\xi (\tau \in Dom(f(\eta ))\wedge f(\eta )(\tau )=\tau )\}).$
Proposition 7.3.
![]() $\vdash _{\mathbf {PW}} \psi _\phi (\delta ,\alpha ,f_1)\wedge \psi _\phi (\delta ,\alpha ,f_2)\to f_1=f_2.$
$\vdash _{\mathbf {PW}} \psi _\phi (\delta ,\alpha ,f_1)\wedge \psi _\phi (\delta ,\alpha ,f_2)\to f_1=f_2.$
Proof Suppose that
![]() $\psi _\phi (\delta ,\alpha ,f_1)$
and
$\psi _\phi (\delta ,\alpha ,f_1)$
and
![]() $\psi _\phi (\delta ,\alpha ,f_2)$
. Then
$\psi _\phi (\delta ,\alpha ,f_2)$
. Then
![]() $Dom(f_1)=Dom(f_2)=\alpha $
. We show that
$Dom(f_1)=Dom(f_2)=\alpha $
. We show that
![]() $f_1(\xi )=f_2(\xi )$
for every
$f_1(\xi )=f_2(\xi )$
for every
![]() $\xi \in \alpha $
. For this we use an induction on
$\xi \in \alpha $
. For this we use an induction on
![]() $\xi $
. The claim is obvious for
$\xi $
. The claim is obvious for
![]() $\xi =0$
. So assume that
$\xi =0$
. So assume that
![]() $\xi>0$
and that
$\xi>0$
and that
![]() $f_1(\eta )=f_2(\eta )$
for every
$f_1(\eta )=f_2(\eta )$
for every
![]() $\eta \in \xi $
. By the definition of
$\eta \in \xi $
. By the definition of
![]() $\psi _\phi $
, this implies that both
$\psi _\phi $
, this implies that both
![]() $f_1(\xi )$
and
$f_1(\xi )$
and
![]() $f_2(\xi )$
are the ordering functions of the same set of ordinals. Hence
$f_2(\xi )$
are the ordering functions of the same set of ordinals. Hence
![]() $f_1(\xi )=f_2(\xi )$
.
$f_1(\xi )=f_2(\xi )$
.
Lemma 7.4.
![]() $\vdash _{\mathbf {PW}} \xi <\alpha \wedge \psi _\phi (\delta ,\alpha ,f)\to \psi _\phi (\delta ,\xi ,f\upharpoonright \xi )$
.
$\vdash _{\mathbf {PW}} \xi <\alpha \wedge \psi _\phi (\delta ,\alpha ,f)\to \psi _\phi (\delta ,\xi ,f\upharpoonright \xi )$
.
Proof Immediate from the definition of
![]() $\psi _\phi $
.
$\psi _\phi $
.
Proposition 7.5.
![]() $\vdash _{\mathbf {PW}} \forall \delta \forall \alpha \exists !f\; \psi _\phi (\delta ,\alpha ,f)$
.
$\vdash _{\mathbf {PW}} \forall \delta \forall \alpha \exists !f\; \psi _\phi (\delta ,\alpha ,f)$
.
Proof If
![]() $\alpha =0$
then
$\alpha =0$
then
![]() $f=\emptyset $
is the only f such that
$f=\emptyset $
is the only f such that
![]() $\psi _\phi (\delta ,\alpha ,f)$
. So assume that
$\psi _\phi (\delta ,\alpha ,f)$
. So assume that
![]() $\alpha>0$
. Since
$\alpha>0$
. Since
![]() $\psi _\phi $
is absolute, it follows by [Unif] from Proposition 7.3 that
$\psi _\phi $
is absolute, it follows by [Unif] from Proposition 7.3 that
 $$ \begin{align*}(\star)\ \ &\vdash_{\mathbf{PW}} \forall\xi\in\alpha\exists f \psi_\phi(\delta,\xi,f)\to \exists!g(Fun(g)\wedge Dom(g)\\&\quad=\alpha\wedge\forall\xi\in\alpha \psi_\phi(\delta,\xi,g(\xi))).\end{align*} $$
$$ \begin{align*}(\star)\ \ &\vdash_{\mathbf{PW}} \forall\xi\in\alpha\exists f \psi_\phi(\delta,\xi,f)\to \exists!g(Fun(g)\wedge Dom(g)\\&\quad=\alpha\wedge\forall\xi\in\alpha \psi_\phi(\delta,\xi,g(\xi))).\end{align*} $$
Now let
![]() $\delta $
be an ordinal. By Proposition 7.3, it suffices to prove in
$\delta $
be an ordinal. By Proposition 7.3, it suffices to prove in
![]() $\mathbf {PW}$
that
$\mathbf {PW}$
that
![]() $\forall \alpha \exists f \psi _\phi (\delta ,\alpha ,f)$
. For this we use an induction on
$\forall \alpha \exists f \psi _\phi (\delta ,\alpha ,f)$
. For this we use an induction on
![]() $\alpha $
. The claim is obvious in case
$\alpha $
. The claim is obvious in case
![]() $\alpha =0$
or
$\alpha =0$
or
![]() $\alpha =1$
. So assume that
$\alpha =1$
. So assume that
![]() $\alpha>1$
and that
$\alpha>1$
and that
![]() $\forall \xi \in \alpha \exists f \psi _\phi (\delta ,\xi ,f)$
. Using
$\forall \xi \in \alpha \exists f \psi _\phi (\delta ,\xi ,f)$
. Using
![]() $(\star )$
, this implies that there is a function g such that
$(\star )$
, this implies that there is a function g such that
![]() $Dom(g)=\alpha $
and
$Dom(g)=\alpha $
and
![]() $\forall \xi \in \alpha \psi _\phi (\delta ,\xi ,g(\xi ))$
. Now we have two cases to consider:
$\forall \xi \in \alpha \psi _\phi (\delta ,\xi ,g(\xi ))$
. Now we have two cases to consider:
-
•
 $\alpha =S(\xi _0)$
for some
$\alpha =S(\xi _0)$
for some
 $\xi _0$
. then we let
$\xi _0$
. then we let
 $f=g(\xi _0)\cup \{\langle \xi _0,o \rangle \}$
, where o is the ordering function of
$f=g(\xi _0)\cup \{\langle \xi _0,o \rangle \}$
, where o is the ordering function of
 $\{\tau \in \delta \!\mid \!\forall \eta <\xi _0(\tau \in Dom(f(\eta ))\wedge f(\eta )(\tau )=\tau )\})$
.
$\{\tau \in \delta \!\mid \!\forall \eta <\xi _0(\tau \in Dom(f(\eta ))\wedge f(\eta )(\tau )=\tau )\})$
. -
•
 $\alpha $
is a limit ordinal. Then for
$\alpha $
is a limit ordinal. Then for
 $\xi <\alpha $
let
$\xi <\alpha $
let
 $f(\xi )=g(S(\xi ))(\xi )$
.
$f(\xi )=g(S(\xi ))(\xi )$
.
Using Lemma 7.4, it is straightforward to verify in both cases that
![]() $\psi _\phi (\delta ,\alpha ,f)$
.
$\psi _\phi (\delta ,\alpha ,f)$
.
Proposition 7.5 allows us to apply [OpI] and introduce in
![]() $\mathbf {PW}$
a new operation symbol
$\mathbf {PW}$
a new operation symbol
![]() $F_\phi $
together with:
$F_\phi $
together with:
AXIOM
![]() $_{F_\phi }$
:
$_{F_\phi }$
:
![]() $f=F_\phi (\delta ,\alpha )\leftrightarrow \psi _\phi (\delta ,\alpha ,f).$
$f=F_\phi (\delta ,\alpha )\leftrightarrow \psi _\phi (\delta ,\alpha ,f).$
In other words: for any two ordinals
![]() $\alpha $
and
$\alpha $
and
![]() $\delta $
,
$\delta $
,
![]() $F_\phi (\delta ,\alpha )$
is the unique function that has the properties 2–5 from Definition 7.2.
$F_\phi (\delta ,\alpha )$
is the unique function that has the properties 2–5 from Definition 7.2.
Some other important properties of
![]() $F_\phi $
are given in the next proposition.
$F_\phi $
are given in the next proposition.
Proposition 7.6. The following are theorems of
![]() $\mathbf {PW}$
:
$\mathbf {PW}$
:
-
1. If
 $\alpha>0$
and
$\alpha>0$
and
 $\beta <\delta $
then
$\beta <\delta $
then
 $F_\phi (\delta ,\alpha )(0)(\beta )=\omega ^\beta $
.
$F_\phi (\delta ,\alpha )(0)(\beta )=\omega ^\beta $
. -
2. If
 $\alpha _1<\alpha _2$
then
$\alpha _1<\alpha _2$
then
 $F_\phi (\delta ,\alpha _1)=F_\phi (\delta ,\alpha _2)\upharpoonright \alpha _1$
.
$F_\phi (\delta ,\alpha _1)=F_\phi (\delta ,\alpha _2)\upharpoonright \alpha _1$
. -
3. If
 $\delta _1<\delta _2$
then for every
$\delta _1<\delta _2$
then for every
 $\xi <\alpha :\ Dom(F_\phi (\delta _1,\alpha )(\xi ))$
is an initial segment of
$\xi <\alpha :\ Dom(F_\phi (\delta _1,\alpha )(\xi ))$
is an initial segment of
 $Dom(F_\phi (\delta _2,\alpha )(\xi ))$
, and
$Dom(F_\phi (\delta _2,\alpha )(\xi ))$
, and
 $F_\phi (\delta _1,\alpha )(\xi )=F_\phi (\delta _2,\alpha )(\xi )\upharpoonright Dom(F_\phi (\delta _1,\alpha )(\xi ))$
.
$F_\phi (\delta _1,\alpha )(\xi )=F_\phi (\delta _2,\alpha )(\xi )\upharpoonright Dom(F_\phi (\delta _1,\alpha )(\xi ))$
. -
4. If
 $\xi _1<\xi _2$
then for every
$\xi _1<\xi _2$
then for every
 $\beta _2\in Dom(F_\phi (\delta ,\alpha )(\xi _2))$
there exists
$\beta _2\in Dom(F_\phi (\delta ,\alpha )(\xi _2))$
there exists
 $\beta _1\geq \beta _2$
such that
$\beta _1\geq \beta _2$
such that
 $\beta _1\in Dom(F_\phi (\delta ,\alpha )(\xi _1))$
, and
$\beta _1\in Dom(F_\phi (\delta ,\alpha )(\xi _1))$
, and
 $F_\phi (\delta ,\alpha )(\xi _2)(\beta _2)=F_\phi (\delta ,\alpha )(\xi _1)(\beta _1)$
.
$F_\phi (\delta ,\alpha )(\xi _2)(\beta _2)=F_\phi (\delta ,\alpha )(\xi _1)(\beta _1)$
. -
5. If
 $\xi <\alpha $
and
$\xi <\alpha $
and
 $\beta \in Dom(F_\phi (\delta ,\alpha )(\xi ))$
then there exists
$\beta \in Dom(F_\phi (\delta ,\alpha )(\xi ))$
then there exists
 $\eta <\delta $
such that
$\eta <\delta $
such that
 $F_\phi (\delta ,\alpha )(\xi )(\beta )=\omega ^\eta $
. In particular,
$F_\phi (\delta ,\alpha )(\xi )(\beta )=\omega ^\eta $
. In particular,
 $F_\phi (\delta ,\alpha )(\xi )(\beta )>0$
.
$F_\phi (\delta ,\alpha )(\xi )(\beta )>0$
. -
6. If
 $\xi <\alpha $
and
$\xi <\alpha $
and
 $\beta \in Dom(F_\phi (\delta ,\alpha )(\xi ))$
then
$\beta \in Dom(F_\phi (\delta ,\alpha )(\xi ))$
then
 $F_\phi (\delta ,\alpha )(\xi )(\beta )\geq max(\xi ,\beta )$
.
$F_\phi (\delta ,\alpha )(\xi )(\beta )\geq max(\xi ,\beta )$
.
Proof
-
1. Immediate from AXIOM
 $_{F_\phi }$
and Definition 7.2.
$_{F_\phi }$
and Definition 7.2. -
2. Immediate from AXIOM
 $_{F_\phi }$
and Lemma 7.4.
$_{F_\phi }$
and Lemma 7.4. -
3. Induction on
 $\xi $
. The claim is obvious for
$\xi $
. The claim is obvious for
 $\xi =0$
by the first item. Now suppose that
$\xi =0$
by the first item. Now suppose that
 $\xi>0$
, and that for every
$\xi>0$
, and that for every
 $\eta <\xi $
it holds that
$\eta <\xi $
it holds that
 $Dom(F_\phi (\delta _1,\alpha )(\eta ))$
is an initial segment of
$Dom(F_\phi (\delta _1,\alpha )(\eta ))$
is an initial segment of
 $Dom(F_\phi (\delta _2,\alpha )(\eta ))$
, and
$Dom(F_\phi (\delta _2,\alpha )(\eta ))$
, and
 $F_\phi (\delta _1,\alpha )(\eta )=F_\phi (\delta _2,\alpha )(\eta )\upharpoonright Dom(F_\phi (\delta _1,\alpha )(\eta ))$
. For
$F_\phi (\delta _1,\alpha )(\eta )=F_\phi (\delta _2,\alpha )(\eta )\upharpoonright Dom(F_\phi (\delta _1,\alpha )(\eta ))$
. For
 $i=1,2$
let Then
$i=1,2$
let Then $$ \begin{align*}A_i= \{\tau\in\delta_i\mid\forall\eta<\xi(\tau\in Dom(F_\phi(\delta_i,\alpha)(\eta))\wedge F_\phi(\delta_i,\alpha)(\eta)(\tau)=\tau)\}.\end{align*} $$
$$ \begin{align*}A_i= \{\tau\in\delta_i\mid\forall\eta<\xi(\tau\in Dom(F_\phi(\delta_i,\alpha)(\eta))\wedge F_\phi(\delta_i,\alpha)(\eta)(\tau)=\tau)\}.\end{align*} $$
 $A_1=A_2\cap \delta _1$
by our induction hypothesis. Since
$A_1=A_2\cap \delta _1$
by our induction hypothesis. Since
 $F_\phi (\delta _i,\alpha )(\xi )$
is the ordering function of
$F_\phi (\delta _i,\alpha )(\xi )$
is the ordering function of
 $A_i$
(
$A_i$
(
 $i=1,2$
), this implies the claim for
$i=1,2$
), this implies the claim for
 $\xi $
.
$\xi $
.
-
4. Immediate from the fact that
 $F_\phi (\delta ,\alpha )(\xi _2)$
is the ordering function of a certain subset of
$F_\phi (\delta ,\alpha )(\xi _2)$
is the ordering function of a certain subset of
 $Im(F_\phi (\delta ,\alpha )(\xi _1))$
.
$Im(F_\phi (\delta ,\alpha )(\xi _1))$
. -
5. Immediate from the previous item and the fact that
 $F_\phi (\delta ,\alpha )(0)(\eta )=\omega ^\eta $
.
$F_\phi (\delta ,\alpha )(0)(\eta )=\omega ^\eta $
. -
6. That
 $F_\phi (\delta ,\alpha )(\xi )(\beta )\geq \beta $
follows from Proposition 6.9 in case
$F_\phi (\delta ,\alpha )(\xi )(\beta )\geq \beta $
follows from Proposition 6.9 in case
 $\xi>0$
, and from the fact that
$\xi>0$
, and from the fact that
 $\omega ^\beta>\beta $
in case
$\omega ^\beta>\beta $
in case
 $\xi =0$
.
$\xi =0$
.That
 $F_\phi (\delta ,\alpha )(\xi )(\beta )\geq \xi $
is shown by induction on
$F_\phi (\delta ,\alpha )(\xi )(\beta )\geq \xi $
is shown by induction on
 $\xi $
. It is certainly true if
$\xi $
. It is certainly true if
 $\xi =0$
. Suppose that
$\xi =0$
. Suppose that
 $\xi>0$
. Let
$\xi>0$
. Let
 $\eta <\xi $
. Then item 3 of this proposition and the induction hypothesis for
$\eta <\xi $
. Then item 3 of this proposition and the induction hypothesis for
 $\eta $
together imply that
$\eta $
together imply that
 $\eta \leq F_\phi (\delta ,\alpha )(\xi )(\beta )$
. Since this is true for every
$\eta \leq F_\phi (\delta ,\alpha )(\xi )(\beta )$
. Since this is true for every
 $\eta <\xi $
, it follows that
$\eta <\xi $
, it follows that
 $\xi \leq F_\phi (\delta ,\alpha )(\xi )(\beta )$
.
$\xi \leq F_\phi (\delta ,\alpha )(\xi )(\beta )$
.
Next we introduce a ternary
![]() $\Sigma $
-formula that expresses (as we show below) the graph of the binary operation
$\Sigma $
-formula that expresses (as we show below) the graph of the binary operation
![]() $\phi $
on ordinals.
$\phi $
on ordinals.
Definition 7.7.
![]() $\varphi _\phi (\alpha ,\beta ,\gamma )$
is the following
$\varphi _\phi (\alpha ,\beta ,\gamma )$
is the following
![]() $\Sigma $
-formula:
$\Sigma $
-formula:
Proposition 7.8.
![]() $\vdash _{\mathbf {PW}} \varphi _\phi (\alpha ,\beta ,\gamma )\to (\alpha \leq \gamma \wedge \beta \leq \gamma )$
.
$\vdash _{\mathbf {PW}} \varphi _\phi (\alpha ,\beta ,\gamma )\to (\alpha \leq \gamma \wedge \beta \leq \gamma )$
.
Proof This follows from the last item of Proposition 7.6.
Proposition 7.9.
![]() $\vdash _{\mathbf {PW}} \varphi _\phi (\alpha ,\beta ,\gamma _1)\wedge \varphi _\phi (\alpha ,\beta ,\gamma _2)\to \gamma _1=\gamma _2$
.
$\vdash _{\mathbf {PW}} \varphi _\phi (\alpha ,\beta ,\gamma _1)\wedge \varphi _\phi (\alpha ,\beta ,\gamma _2)\to \gamma _1=\gamma _2$
.
Proof Suppose that
![]() $\varphi _\phi (\alpha ,\beta ,\gamma _1)$
and
$\varphi _\phi (\alpha ,\beta ,\gamma _1)$
and
![]() $\varphi _\phi (\alpha ,\beta ,\gamma _2)$
. Then there exist
$\varphi _\phi (\alpha ,\beta ,\gamma _2)$
. Then there exist
![]() $\delta _1$
and
$\delta _1$
and
![]() $\delta _2$
such that
$\delta _2$
such that
![]() $\beta \in Dom(F_\phi (\delta _1,S(\alpha ))(\alpha )) \wedge F_\phi (\delta _1,S(\alpha ))(\alpha )(\beta )=\gamma _1$
, and also
$\beta \in Dom(F_\phi (\delta _1,S(\alpha ))(\alpha )) \wedge F_\phi (\delta _1,S(\alpha ))(\alpha )(\beta )=\gamma _1$
, and also
![]() $\beta \in Dom(F_\phi (\delta _2,S(\alpha ))(\alpha )) \wedge F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta )=\gamma _2$
. Without loss in generality, we may assume that
$\beta \in Dom(F_\phi (\delta _2,S(\alpha ))(\alpha )) \wedge F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta )=\gamma _2$
. Without loss in generality, we may assume that
![]() $\delta _1\leq \delta _2$
. Then it follows from item 3 of Proposition 7.6 that
$\delta _1\leq \delta _2$
. Then it follows from item 3 of Proposition 7.6 that
![]() $F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta )=\gamma _1$
. Hence
$F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta )=\gamma _1$
. Hence
![]() $\gamma _1=\gamma _2$
.
$\gamma _1=\gamma _2$
.
To follow the proof of the next theorem, it would be helpful to remember that the intend meaning of the formula ‘
![]() $\varphi _{\phi }(\alpha ,\beta ,\gamma )$
’ of
$\varphi _{\phi }(\alpha ,\beta ,\gamma )$
’ of
![]() $\mathbf {PW}$
is ‘
$\mathbf {PW}$
is ‘
![]() $\phi (\alpha ,\beta )=\gamma $
’ (which at present is a formula only in the metalanguage of
$\phi (\alpha ,\beta )=\gamma $
’ (which at present is a formula only in the metalanguage of
![]() $\mathbf {PW}$
).
$\mathbf {PW}$
).
Theorem 7.10.
![]() $\vdash _{\mathbf {PW}} \forall \alpha \forall \beta \exists !\gamma \varphi _{\phi }(\alpha ,\beta ,\gamma ).$
$\vdash _{\mathbf {PW}} \forall \alpha \forall \beta \exists !\gamma \varphi _{\phi }(\alpha ,\beta ,\gamma ).$
Proof The uniqueness part follows from Proposition 7.9. We prove the existence part by using an
![]() $\in $
-induction on
$\in $
-induction on
![]() $\alpha $
in
$\alpha $
in
![]() $\mathbf {PW}$
to simultaneously show:
$\mathbf {PW}$
to simultaneously show:
-
(a)
 $\forall \beta \exists \gamma \varphi _{\phi }(\alpha ,\beta ,\gamma ).$
$\forall \beta \exists \gamma \varphi _{\phi }(\alpha ,\beta ,\gamma ).$
-
(b)
 $\forall \beta \forall \gamma ([Fun(f)\wedge Fun(g)\wedge Dom(f)=Dom(g)=\omega \wedge \forall n\in \omega \varphi _{\phi }(\alpha , f(n),g(n))$
$\forall \beta \forall \gamma ([Fun(f)\wedge Fun(g)\wedge Dom(f)=Dom(g)=\omega \wedge \forall n\in \omega \varphi _{\phi }(\alpha , f(n),g(n))$
 $\wedge \beta \!=\!sup\{f(n)\!\mid \!n\in \omega \}\wedge \gamma =sup\{g(n)\mid n\in \omega \}] \to \varphi _{\phi }(\alpha ,\beta ,\gamma )).$
$\wedge \beta \!=\!sup\{f(n)\!\mid \!n\in \omega \}\wedge \gamma =sup\{g(n)\mid n\in \omega \}] \to \varphi _{\phi }(\alpha ,\beta ,\gamma )).$
The case
![]() $\alpha =0$
is easy, since
$\alpha =0$
is easy, since
![]() $\vdash _{\mathbf {PW}} \varphi _{\phi }(0,\beta ,\gamma )\leftrightarrow \omega ^\beta =\gamma $
.
$\vdash _{\mathbf {PW}} \varphi _{\phi }(0,\beta ,\gamma )\leftrightarrow \omega ^\beta =\gamma $
.
Now fix some
![]() $\alpha>0$
, and assume that (a) and (b) are true for every
$\alpha>0$
, and assume that (a) and (b) are true for every
![]() $\xi \in \alpha $
. In particular, we have that
$\xi \in \alpha $
. In particular, we have that
![]() $\forall \xi \in \alpha \forall \beta \exists \gamma \varphi _{\phi }(\xi ,\beta ,\gamma )$
. This implies
$\forall \xi \in \alpha \forall \beta \exists \gamma \varphi _{\phi }(\xi ,\beta ,\gamma )$
. This implies
Using Proposition 7.9, an application of [Unif] yields
 $$ \begin{align*}(2)\; &\vdash_{\mathbf{PW}}\forall\xi\in\alpha\exists\gamma \varphi_{\phi}(\xi,\beta,\gamma))\\&\quad\to\exists!f (Fun(f)\wedge Dom(f)\!=\!\alpha\wedge\forall \xi\in\alpha \varphi_{\phi}(\xi,\beta,f(\xi))).\end{align*} $$
$$ \begin{align*}(2)\; &\vdash_{\mathbf{PW}}\forall\xi\in\alpha\exists\gamma \varphi_{\phi}(\xi,\beta,\gamma))\\&\quad\to\exists!f (Fun(f)\wedge Dom(f)\!=\!\alpha\wedge\forall \xi\in\alpha \varphi_{\phi}(\xi,\beta,f(\xi))).\end{align*} $$
From (1) and (2), we get
Let
![]() $\theta (\beta ,\tau )$
be the following formula:
$\theta (\beta ,\tau )$
be the following formula:
Then
![]() $\theta $
is in
$\theta $
is in
![]() $\Sigma $
, and (3) implies that the following holds for the given
$\Sigma $
, and (3) implies that the following holds for the given
![]() $\alpha $
:
$\alpha $
:
Next we show that for every ordinal
![]() $\beta $
there exists a bigger ordinal
$\beta $
there exists a bigger ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $\varphi _{\phi }(\xi ,\gamma ,\gamma )$
holds for every
$\varphi _{\phi }(\xi ,\gamma ,\gamma )$
holds for every
![]() $\xi \in \alpha $
. So fix an ordinal
$\xi \in \alpha $
. So fix an ordinal
![]() $\beta $
. From (4) it follows by Theorem 6.7 that there exists an
$\beta $
. From (4) it follows by Theorem 6.7 that there exists an
![]() $\omega $
-sequence g such that
$\omega $
-sequence g such that
![]() $g(0)=\beta +1$
, and
$g(0)=\beta +1$
, and
![]() $\theta \{g(n),g(n+1)\}$
for every
$\theta \{g(n),g(n+1)\}$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\gamma =sup\{g(n)\mid n\in \omega \}$
. Then
$\gamma =sup\{g(n)\mid n\in \omega \}$
. Then
![]() $g(n)\leq \gamma $
for every
$g(n)\leq \gamma $
for every
![]() $n\in \omega $
. Hence
$n\in \omega $
. Hence
![]() $\beta <\gamma $
(since
$\beta <\gamma $
(since
![]() $\beta <g(0)$
). We show that
$\beta <g(0)$
). We show that
![]() $\varphi _{\phi }(\xi ,\gamma ,\gamma )$
for
$\varphi _{\phi }(\xi ,\gamma ,\gamma )$
for
![]() $\xi <\alpha $
. So fix
$\xi <\alpha $
. So fix
![]() $\xi \in \alpha $
. (1) implies that
$\xi \in \alpha $
. (1) implies that
![]() $\forall n\in \omega \exists \gamma ^\prime \varphi _{\phi }(\xi ,g(n),\gamma ^\prime )$
. Using Proposition 7.9 and an application of [Unif], this yields a function d such that
$\forall n\in \omega \exists \gamma ^\prime \varphi _{\phi }(\xi ,g(n),\gamma ^\prime )$
. Using Proposition 7.9 and an application of [Unif], this yields a function d such that
![]() $\varphi _{\phi }(\xi ,g(n),d(n))$
for every
$\varphi _{\phi }(\xi ,g(n),d(n))$
for every
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $D= \{d(n)\mid n\in \omega \}$
. Part (b) of the induction hypothesis entails that
$D= \{d(n)\mid n\in \omega \}$
. Part (b) of the induction hypothesis entails that
![]() $\varphi _{\phi }(\xi ,\gamma ,D)$
. Hence
$\varphi _{\phi }(\xi ,\gamma ,D)$
. Hence
![]() $\gamma \leq D$
by Proposition 7.8. On the other hand, the fact that
$\gamma \leq D$
by Proposition 7.8. On the other hand, the fact that
![]() $\theta \{g(n),g(n+1)\}$
implies that there is a function f such that
$\theta \{g(n),g(n+1)\}$
implies that there is a function f such that
![]() $Dom(f)=\alpha $
and for every
$Dom(f)=\alpha $
and for every
![]() $\eta <\alpha $
,
$\eta <\alpha $
,
![]() $\varphi _{\phi }(\eta ,g(n),f(\eta ))\wedge g(n+1)\geq f(\eta )$
. In particular, (i)
$\varphi _{\phi }(\eta ,g(n),f(\eta ))\wedge g(n+1)\geq f(\eta )$
. In particular, (i)
![]() $\varphi _{\phi }(\xi ,g(n),f(\xi ))$
and (ii)
$\varphi _{\phi }(\xi ,g(n),f(\xi ))$
and (ii)
![]() $g(n+1)\geq f(\xi )$
. By Proposition 7.9, (i) entails that
$g(n+1)\geq f(\xi )$
. By Proposition 7.9, (i) entails that
![]() $f(\xi )=d(n)$
. Hence (ii) implies that
$f(\xi )=d(n)$
. Hence (ii) implies that
![]() $d(n)\leq g(n+1)$
. This is true for every
$d(n)\leq g(n+1)$
. This is true for every
![]() $n\in \omega $
. Hence
$n\in \omega $
. Hence
![]() $D\leq \gamma $
. It follows that
$D\leq \gamma $
. It follows that
![]() $D=\gamma $
, implying that
$D=\gamma $
, implying that
![]() $\varphi _{\phi }(\xi ,\gamma ,\gamma )$
.
$\varphi _{\phi }(\xi ,\gamma ,\gamma )$
.
Now we prove (a) for
![]() $\alpha $
, i.e., that for every
$\alpha $
, i.e., that for every
![]() $\beta $
there is
$\beta $
there is
![]() $\gamma $
such that
$\gamma $
such that
![]() $\varphi _{\phi }(\alpha ,\beta ,\gamma )$
. We do this by induction on
$\varphi _{\phi }(\alpha ,\beta ,\gamma )$
. We do this by induction on
![]() $\beta $
. So suppose that
$\beta $
. So suppose that
![]() $\forall \eta <\beta \exists \gamma \varphi _{\phi }(\alpha ,\eta ,\gamma )$
. Using Proposition 7.9 and [Unif], this provides a function h with domain
$\forall \eta <\beta \exists \gamma \varphi _{\phi }(\alpha ,\eta ,\gamma )$
. Using Proposition 7.9 and [Unif], this provides a function h with domain
![]() $\beta $
such that
$\beta $
such that
![]() $\forall \eta <\beta \varphi _{\phi }(\alpha ,\eta ,h(\eta ))$
. Let
$\forall \eta <\beta \varphi _{\phi }(\alpha ,\eta ,h(\eta ))$
. Let
![]() $\gamma _0$
be the least ordinal
$\gamma _0$
be the least ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $\varphi _{\phi }(\xi ,\gamma ,\gamma )$
for every
$\varphi _{\phi }(\xi ,\gamma ,\gamma )$
for every
![]() $\xi \in \alpha $
, and
$\xi \in \alpha $
, and
![]() $\gamma> sup\{h(\eta )\mid \eta <\beta \}$
. (
$\gamma> sup\{h(\eta )\mid \eta <\beta \}$
. (
![]() $\gamma _0$
exists by the claim we have just proved.) By definition, the first property of
$\gamma _0$
exists by the claim we have just proved.) By definition, the first property of
![]() $\gamma _0$
means that
$\gamma _0$
means that
By the second item of Proposition 7.6, this implies
Let
![]() $A(\xi ,\delta ):=\gamma _0\in Dom(F_\phi (\delta ,S(\alpha ))(\xi )) \wedge F_\phi (\delta ,S(\alpha ))(\xi )(\gamma _0)=\gamma _0$
, and let
$A(\xi ,\delta ):=\gamma _0\in Dom(F_\phi (\delta ,S(\alpha ))(\xi )) \wedge F_\phi (\delta ,S(\alpha ))(\xi )(\gamma _0)=\gamma _0$
, and let
![]() $B(\xi ,\delta ):=A\wedge \forall \delta ^\prime <\delta \neg A\{\delta ^\prime /\delta \}$
. (7) implies that
$B(\xi ,\delta ):=A\wedge \forall \delta ^\prime <\delta \neg A\{\delta ^\prime /\delta \}$
. (7) implies that
![]() $\forall \xi <\alpha \exists \delta \;B(\xi ,\delta )$
. Obviously,
$\forall \xi <\alpha \exists \delta \;B(\xi ,\delta )$
. Obviously,
![]() $\vdash _{\mathbf {PW}} B(\xi ,\delta _1)\wedge B(\xi ,\delta _2)\to \delta _1=\delta _2$
. Since B is absolute (because A is), we can use [Unif] in order to infer from the last two facts that there is a function q such that
$\vdash _{\mathbf {PW}} B(\xi ,\delta _1)\wedge B(\xi ,\delta _2)\to \delta _1=\delta _2$
. Since B is absolute (because A is), we can use [Unif] in order to infer from the last two facts that there is a function q such that
![]() $\forall \xi <\alpha B(\xi ,q(\xi ))$
. This, in turn, implies that
$\forall \xi <\alpha B(\xi ,q(\xi ))$
. This, in turn, implies that
![]() $\forall \xi <\alpha A(\xi ,q(\xi ))$
. Let
$\forall \xi <\alpha A(\xi ,q(\xi ))$
. Let
![]() $\delta _0=sup\{q(\xi )\mid \xi <\alpha \}$
. By the third item of Proposition 7.6, we get from the last claim and the definition of A that
$\delta _0=sup\{q(\xi )\mid \xi <\alpha \}$
. By the third item of Proposition 7.6, we get from the last claim and the definition of A that
Now, by AXIOM
![]() $_{F_\phi }$
and Definition 7.2(5), we have that
$_{F_\phi }$
and Definition 7.2(5), we have that
![]() $Im(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
is
$Im(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
is
![]() $\{\tau \in \delta _0\!\mid \!\forall \eta <\alpha (\tau \in Dom(F_\phi (\delta _0,S(\alpha ))(\eta ))\wedge F_\phi (\delta _0,S(\alpha ))(\eta )(\tau )=\tau )\}$
. Hence (8) implies that
$\{\tau \in \delta _0\!\mid \!\forall \eta <\alpha (\tau \in Dom(F_\phi (\delta _0,S(\alpha ))(\eta ))\wedge F_\phi (\delta _0,S(\alpha ))(\eta )(\tau )=\tau )\}$
. Hence (8) implies that
![]() $\gamma _0\in Im(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
. It follows that there exists
$\gamma _0\in Im(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
. It follows that there exists
![]() $\beta ^\prime $
in
$\beta ^\prime $
in
![]() $Dom(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
such that
$Dom(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
such that
![]() $F_\phi (\delta ,S(\alpha ))(\alpha )(\beta ^\prime )=\gamma _0$
. But for every
$F_\phi (\delta ,S(\alpha ))(\alpha )(\beta ^\prime )=\gamma _0$
. But for every
![]() $\eta <\beta $
,
$\eta <\beta $
,
![]() $\gamma _0> h(\eta )$
. Since
$\gamma _0> h(\eta )$
. Since
![]() $\forall \eta <\beta \varphi _{\phi }(\alpha ,\eta ,h(\eta ))$
, this and Proposition 7.9 imply that
$\forall \eta <\beta \varphi _{\phi }(\alpha ,\eta ,h(\eta ))$
, this and Proposition 7.9 imply that
![]() $\forall \tau \forall \eta <\beta (\varphi _{\phi }(\alpha ,\eta ,\tau )\to \tau <\gamma _0)$
. By definition of
$\forall \tau \forall \eta <\beta (\varphi _{\phi }(\alpha ,\eta ,\tau )\to \tau <\gamma _0)$
. By definition of
![]() $\varphi _{\phi }$
, this means that
$\varphi _{\phi }$
, this means that
![]() $\forall \delta \forall \eta <\beta F_\phi (\delta _0,S(\alpha ))(\alpha )(\eta )<\gamma _0$
. In particular,
$\forall \delta \forall \eta <\beta F_\phi (\delta _0,S(\alpha ))(\alpha )(\eta )<\gamma _0$
. In particular,
![]() $F_\phi (\delta _0,S(\alpha ))(\alpha )(\eta )<\gamma _0$
for every
$F_\phi (\delta _0,S(\alpha ))(\alpha )(\eta )<\gamma _0$
for every
![]() $\eta <\beta $
. Therefore
$\eta <\beta $
. Therefore
![]() $\beta ^\prime \geq \beta $
. It follows that
$\beta ^\prime \geq \beta $
. It follows that
![]() $\beta \in Dom(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
as well (by the definition of an ordering function). Let
$\beta \in Dom(F_\phi (\delta _0,S(\alpha ))(\alpha ))$
as well (by the definition of an ordering function). Let
![]() $\gamma =F_\phi (\delta _0,S(\alpha ))(\alpha )(\beta )$
. Then
$\gamma =F_\phi (\delta _0,S(\alpha ))(\alpha )(\beta )$
. Then
![]() $\varphi _{\phi }(\alpha ,\beta ,\gamma )$
.
$\varphi _{\phi }(\alpha ,\beta ,\gamma )$
.
Finally, we prove that
![]() $\alpha $
satisfies (b) too. So let f and g be functions whose domain is
$\alpha $
satisfies (b) too. So let f and g be functions whose domain is
![]() $\omega $
, and suppose that
$\omega $
, and suppose that
![]() $\forall n\in \omega \varphi _{\phi }(\alpha ,f(n),g(n))$
,
$\forall n\in \omega \varphi _{\phi }(\alpha ,f(n),g(n))$
,
![]() $\beta \!=\!sup\{f(n)\!\mid \!n\in \omega \}$
and
$\beta \!=\!sup\{f(n)\!\mid \!n\in \omega \}$
and
![]() $ \gamma =sup\{g(n)\mid n\in \omega \}$
. Then
$ \gamma =sup\{g(n)\mid n\in \omega \}$
. Then
![]() $\forall n\in \omega \exists \delta (F_\phi (\delta ,S(\alpha ))(\alpha )(f(n))=g(n))$
. With the help of the method used above to infer (8) from (7), we can infer from this that there exists
$\forall n\in \omega \exists \delta (F_\phi (\delta ,S(\alpha ))(\alpha )(f(n))=g(n))$
. With the help of the method used above to infer (8) from (7), we can infer from this that there exists
![]() $\delta $
such that
$\delta $
such that
![]() $\forall n\in \omega (F_\phi (\delta ,S(\alpha ))(\alpha )(f(n))=g(n))$
. Since
$\forall n\in \omega (F_\phi (\delta ,S(\alpha ))(\alpha )(f(n))=g(n))$
. Since
![]() $\psi _\phi (\delta ,S(\alpha ),F_\phi (\delta ,S(\alpha )))$
by AXIOM
$\psi _\phi (\delta ,S(\alpha ),F_\phi (\delta ,S(\alpha )))$
by AXIOM
![]() $_{F_\phi }$
, and
$_{F_\phi }$
, and
![]() $0<\alpha <S(\alpha )$
, this implies that
$0<\alpha <S(\alpha )$
, this implies that
![]() $Ord(F_\phi (\delta ,S(\alpha ))(\alpha ),\{\tau \in \delta \mid \forall \xi <\alpha F_\phi (\delta ,S(\alpha ))(\xi )(\tau )=\tau \}$
. It follows that for every
$Ord(F_\phi (\delta ,S(\alpha ))(\alpha ),\{\tau \in \delta \mid \forall \xi <\alpha F_\phi (\delta ,S(\alpha ))(\xi )(\tau )=\tau \}$
. It follows that for every
![]() $n\in \omega $
we have that
$n\in \omega $
we have that
![]() $\forall \xi <\alpha F_\phi (\delta ,S(\alpha ))(\xi )(g(n))=g(n)$
. By item 2 of Proposition 7.6 this implies that
$\forall \xi <\alpha F_\phi (\delta ,S(\alpha ))(\xi )(g(n))=g(n)$
. By item 2 of Proposition 7.6 this implies that
![]() $\forall \xi <\alpha F_\phi (\delta ,S(\xi ))(\xi )(g(n))=g(n)$
, and so also
$\forall \xi <\alpha F_\phi (\delta ,S(\xi ))(\xi )(g(n))=g(n)$
, and so also
![]() $\forall \xi <\alpha \varphi _\phi (\xi ,g(n),g(n))$
(by the definition of
$\forall \xi <\alpha \varphi _\phi (\xi ,g(n),g(n))$
(by the definition of
![]() $\varphi _\phi $
). Hence the induction hypothesis for
$\varphi _\phi $
). Hence the induction hypothesis for
![]() $\xi <\alpha $
entails that
$\xi <\alpha $
entails that
![]() $\forall \xi <\alpha \varphi _\phi (\xi ,\gamma ,\gamma )$
. It follows that
$\forall \xi <\alpha \varphi _\phi (\xi ,\gamma ,\gamma )$
. It follows that
![]() $\forall \xi <\alpha \exists \delta ^\prime (F_\phi (\delta ^\prime ,S(\xi ))(\xi )(\gamma )=\gamma )$
. Applying again the method used to infer (8) from (7), we get from that an ordinal
$\forall \xi <\alpha \exists \delta ^\prime (F_\phi (\delta ^\prime ,S(\xi ))(\xi )(\gamma )=\gamma )$
. Applying again the method used to infer (8) from (7), we get from that an ordinal
![]() $\delta $
such that
$\delta $
such that
![]() $\forall \xi <\alpha (F_\phi (\delta ,S(\xi ))(\xi )(\gamma )=\gamma )$
. Therefore
$\forall \xi <\alpha (F_\phi (\delta ,S(\xi ))(\xi )(\gamma )=\gamma )$
. Therefore
![]() $\forall \xi <\alpha (F_\phi (\delta ,S(\alpha ))(\xi )(\gamma )=\gamma )$
(by the second item of Proposition 7.6). It follows that
$\forall \xi <\alpha (F_\phi (\delta ,S(\alpha ))(\xi )(\gamma )=\gamma )$
(by the second item of Proposition 7.6). It follows that
![]() $\gamma \in Im(r)$
, where
$\gamma \in Im(r)$
, where
![]() $r=F_\phi (\delta ,S(\alpha ))(\alpha )$
. Hence
$r=F_\phi (\delta ,S(\alpha ))(\alpha )$
. Hence
![]() $\gamma =r(\beta ^\prime )$
for some
$\gamma =r(\beta ^\prime )$
for some
![]() $\beta ^\prime $
. Since r is monotonic, and
$\beta ^\prime $
. Since r is monotonic, and
![]() $\gamma \geq g(n)$
for every
$\gamma \geq g(n)$
for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\beta ^\prime \geq f(n)$
for every
$\beta ^\prime \geq f(n)$
for every
![]() $n\in \omega $
, and so
$n\in \omega $
, and so
![]() $\beta ^\prime \geq \beta $
. It follows that
$\beta ^\prime \geq \beta $
. It follows that
![]() $\beta $
is in the domain of r, and so
$\beta $
is in the domain of r, and so
![]() $\gamma =r(\beta ^\prime )\geq r(\beta )$
. On the other hand,
$\gamma =r(\beta ^\prime )\geq r(\beta )$
. On the other hand,
![]() $r(\beta )\geq r(f(n))=g(n)$
for every
$r(\beta )\geq r(f(n))=g(n)$
for every
![]() $n\in \omega $
, and so
$n\in \omega $
, and so
![]() $r(\beta )\geq \gamma $
. Hence
$r(\beta )\geq \gamma $
. Hence
![]() $r(\beta )=\gamma $
, and so
$r(\beta )=\gamma $
, and so
![]() $\varphi _\phi (\alpha ,\beta ,\gamma )$
.
$\varphi _\phi (\alpha ,\beta ,\gamma )$
.
Theorem 7.10 allows us to apply [OpI] and introduce in
![]() $\mathbf {PW}$
a new operation symbol
$\mathbf {PW}$
a new operation symbol
![]() $\phi $
together with the following axiom:
$\phi $
together with the following axiom:
AXIOM
![]() $_{\phi }$
:
$_{\phi }$
:
![]() $\gamma =\phi (\alpha ,\beta )\leftrightarrow \phi (\alpha ,\beta ,\gamma ).$
$\gamma =\phi (\alpha ,\beta )\leftrightarrow \phi (\alpha ,\beta ,\gamma ).$
The standard characteristic properties of
![]() $\phi $
are given in the next proposition.
$\phi $
are given in the next proposition.
Proposition 7.11. The following are theorems of
![]() $\mathbf {PW}$
:
$\mathbf {PW}$
:
-
1.
 $\beta _1<\beta _2\to \phi (\alpha ,\beta _1)<\phi (\alpha ,\beta _2).$
$\beta _1<\beta _2\to \phi (\alpha ,\beta _1)<\phi (\alpha ,\beta _2).$
-
2.
 $\phi (0,\beta )=\omega ^\beta $
.
$\phi (0,\beta )=\omega ^\beta $
. -
3.
 $\alpha>0\to \forall \gamma (\exists \beta (\gamma =\phi (\alpha ,\beta ))\leftrightarrow \forall \xi <\alpha (\phi (\xi ,\gamma )=\gamma )).$
$\alpha>0\to \forall \gamma (\exists \beta (\gamma =\phi (\alpha ,\beta ))\leftrightarrow \forall \xi <\alpha (\phi (\xi ,\gamma )=\gamma )).$
Proof
-
1. Let
 $\phi (\alpha ,\beta _1)=\gamma _1$
,
$\phi (\alpha ,\beta _1)=\gamma _1$
,
 $\phi (\alpha ,\beta _2)=\gamma _2$
. Then
$\phi (\alpha ,\beta _2)=\gamma _2$
. Then
 $\varphi _\phi (\alpha ,\beta _1,\gamma _1)$
and
$\varphi _\phi (\alpha ,\beta _1,\gamma _1)$
and
 $\varphi _\phi (\alpha ,\beta _2,\gamma _2)$
. Hence there exist
$\varphi _\phi (\alpha ,\beta _2,\gamma _2)$
. Hence there exist
 $\delta _1$
and
$\delta _1$
and
 $\delta _2$
such that
$\delta _2$
such that
 $ F_\phi (\delta _i,S(\alpha ))(\alpha )(\beta _i)=\gamma _i$
for
$ F_\phi (\delta _i,S(\alpha ))(\alpha )(\beta _i)=\gamma _i$
for
 $i=1,2$
. Without loss in generality, we may assume that
$i=1,2$
. Without loss in generality, we may assume that
 $\delta _1\leq \delta _2$
. Then it follows from item 3 of Proposition 7.6 that
$\delta _1\leq \delta _2$
. Then it follows from item 3 of Proposition 7.6 that
 $F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta _1)=\gamma _1$
. Since
$F_\phi (\delta _2,S(\alpha ))(\alpha )(\beta _1)=\gamma _1$
. Since
 $F_\phi (\delta _2,S(\alpha ))(\alpha )$
is an ordering function, it follows that
$F_\phi (\delta _2,S(\alpha ))(\alpha )$
is an ordering function, it follows that
 $\gamma _1<\gamma _2$
.
$\gamma _1<\gamma _2$
. -
2. Immediate from the first item of Proposition 7.6 (and Theorem 7.10).
-
3. Suppose first that
 $\gamma =\phi (\alpha ,\beta )$
. Then
$\gamma =\phi (\alpha ,\beta )$
. Then
 $\varphi _\phi (\alpha ,\beta ,\gamma )$
, and so there exists
$\varphi _\phi (\alpha ,\beta ,\gamma )$
, and so there exists
 $\delta $
such that
$\delta $
such that
 $F_\phi (\delta ,s(\alpha ))(\alpha )(\beta )=\gamma $
. Therefore it follows by AXIOM
$F_\phi (\delta ,s(\alpha ))(\alpha )(\beta )=\gamma $
. Therefore it follows by AXIOM
 $_{F_\phi }$
and Definition 7.2 that
$_{F_\phi }$
and Definition 7.2 that
 $F_\phi (\delta ,S(\alpha ))(\xi )(\gamma )=\gamma $
for every
$F_\phi (\delta ,S(\alpha ))(\xi )(\gamma )=\gamma $
for every
 $\xi <\alpha $
. Hence
$\xi <\alpha $
. Hence
 $F_\phi (\delta ,S(\xi ))(\xi )(\gamma )=\gamma $
for every
$F_\phi (\delta ,S(\xi ))(\xi )(\gamma )=\gamma $
for every
 $\xi <\alpha $
, by the second item of Proposition 7.6. It follows that
$\xi <\alpha $
, by the second item of Proposition 7.6. It follows that
 $\varphi _\phi (\xi ,\gamma ,\gamma )$
, and so
$\varphi _\phi (\xi ,\gamma ,\gamma )$
, and so
 $\phi (\xi ,\gamma )=\gamma $
, for every
$\phi (\xi ,\gamma )=\gamma $
, for every
 $\xi <\alpha $
.
$\xi <\alpha $
.For the converse, let
 $\phi (\xi ,\gamma )=\gamma $
(i.e.,
$\phi (\xi ,\gamma )=\gamma $
(i.e.,
 $\varphi _\phi (\xi ,\gamma ,\gamma )$
) for every
$\varphi _\phi (\xi ,\gamma ,\gamma )$
) for every
 $\xi <\alpha $
. We can show that this implies that there exists
$\xi <\alpha $
. We can show that this implies that there exists
 $\delta $
such that
$\delta $
such that
 $\gamma \in Im(F_\phi (\delta ,s(\alpha ))(\alpha )))$
exactly as we show the same implication for
$\gamma \in Im(F_\phi (\delta ,s(\alpha ))(\alpha )))$
exactly as we show the same implication for
 $\gamma _0$
at the proof of Theorem 7.10. This means that there is
$\gamma _0$
at the proof of Theorem 7.10. This means that there is
 $\beta $
such that
$\beta $
such that
 $F_\phi (\delta ,s(\alpha ))(\alpha ))(\beta )=\gamma $
. Hence, by definition,
$F_\phi (\delta ,s(\alpha ))(\alpha ))(\beta )=\gamma $
. Hence, by definition,
 $\varphi _\phi (\alpha ,\beta ,\gamma )$
, and so there exists
$\varphi _\phi (\alpha ,\beta ,\gamma )$
, and so there exists
 $\beta $
such that
$\beta $
such that
 $\phi (\alpha ,\beta )=\gamma $
.
$\phi (\alpha ,\beta )=\gamma $
.
Corollary 7.12. The following are theorems of
![]() $\mathbf {PW}$
:
$\mathbf {PW}$
:
-
1.
 $\phi (\xi ,\phi (\alpha ,\beta ))=\phi (\alpha ,\beta )$
for every
$\phi (\xi ,\phi (\alpha ,\beta ))=\phi (\alpha ,\beta )$
for every
 $\xi <\alpha $
.
$\xi <\alpha $
. -
2.
 $\alpha>0\to \forall \gamma <\phi (\alpha ,\beta )((\forall \xi <\alpha \phi (\xi ,\gamma )=\gamma ) \to \exists \beta ^\prime <\beta \phi (\alpha ,\beta ^\prime )=\gamma )$
.
$\alpha>0\to \forall \gamma <\phi (\alpha ,\beta )((\forall \xi <\alpha \phi (\xi ,\gamma )=\gamma ) \to \exists \beta ^\prime <\beta \phi (\alpha ,\beta ^\prime )=\gamma )$
. -
3. Let
 $\alpha>0$
, and suppose that the following three conditions are satisfied:
$\alpha>0$
, and suppose that the following three conditions are satisfied:-
(a)
 $\phi (\xi ,\gamma )=\gamma $
for every
$\phi (\xi ,\gamma )=\gamma $
for every
 $\xi <\alpha $
.
$\xi <\alpha $
. -
(b)
 $\phi (\alpha ,\beta ^\prime )<\gamma $
for every
$\phi (\alpha ,\beta ^\prime )<\gamma $
for every
 $\beta ^\prime <\beta $
.
$\beta ^\prime <\beta $
. -
(c)
 $\forall \gamma ^\prime <\gamma [(\forall \xi <\alpha \phi (\xi ,\gamma ^\prime )=\gamma ^\prime ) \to \exists \beta ^\prime <\beta \phi (\alpha ,\beta ^\prime )=\gamma ^\prime ].$
$\forall \gamma ^\prime <\gamma [(\forall \xi <\alpha \phi (\xi ,\gamma ^\prime )=\gamma ^\prime ) \to \exists \beta ^\prime <\beta \phi (\alpha ,\beta ^\prime )=\gamma ^\prime ].$
Then
 $\phi (\alpha ,\beta )=\gamma $
.
$\phi (\alpha ,\beta )=\gamma $
. -
Proof Easily follows from Proposition 7.11.
Proposition 7.13.
![]() $\vdash _{\mathbf {PW}} \alpha \leq \phi (\alpha ,\beta )\wedge \beta \leq \phi (\alpha ,\beta )$
.
$\vdash _{\mathbf {PW}} \alpha \leq \phi (\alpha ,\beta )\wedge \beta \leq \phi (\alpha ,\beta )$
.
Proof Immediate from Proposition 7.8.
Corollary 7.14.
![]() $\mathbf {PW}$
proves that for every ordinal
$\mathbf {PW}$
proves that for every ordinal
![]() $\alpha>0$
and for every ordinal
$\alpha>0$
and for every ordinal
![]() $\gamma $
such that
$\gamma $
such that
![]() $\forall \xi <\alpha \;\phi (\xi ,\gamma )=\gamma $
there exists
$\forall \xi <\alpha \;\phi (\xi ,\gamma )=\gamma $
there exists
![]() $\beta \leq \gamma $
such that
$\beta \leq \gamma $
such that
![]() $\phi (\alpha ,\beta )=\gamma $
.
$\phi (\alpha ,\beta )=\gamma $
.
Proof
![]() $\gamma <\phi (\alpha ,S(\gamma ))$
by Proposition 7.13. Hence the claim follows from item 2 of Corollary 7.12.
$\gamma <\phi (\alpha ,S(\gamma ))$
by Proposition 7.13. Hence the claim follows from item 2 of Corollary 7.12.
Once we have proved Proposition 7.11, all of
![]() $\phi $
’s main properties (as given, e.g., at Section 13 of [Reference Schütte43]) can predicatively be derived using the standard proofs. As an example, we present here the full proof of the following well-know result.
$\phi $
’s main properties (as given, e.g., at Section 13 of [Reference Schütte43]) can predicatively be derived using the standard proofs. As an example, we present here the full proof of the following well-know result.
Proposition 7.15.
![]() $\vdash _{\mathbf {PW}}\forall A(A\neq \emptyset \!\to \! \forall \alpha (\phi (\alpha ,sup\;A)\!=\! sup\{\phi (\alpha ,\beta )\mid \beta \in A\})).$
$\vdash _{\mathbf {PW}}\forall A(A\neq \emptyset \!\to \! \forall \alpha (\phi (\alpha ,sup\;A)\!=\! sup\{\phi (\alpha ,\beta )\mid \beta \in A\})).$
Proof The claim is obviously true for
![]() $\alpha =0 $
. So assume that
$\alpha =0 $
. So assume that
![]() $\alpha>0$
. Using
$\alpha>0$
. Using
![]() $\in $
-induction on
$\in $
-induction on
![]() $\alpha $
, we show that
$\alpha $
, we show that
![]() $\phi (\alpha ,\beta )=\gamma $
, where
$\phi (\alpha ,\beta )=\gamma $
, where
![]() $\gamma =sup\{\phi (\alpha ,\tau )\mid \tau \in A\}$
and
$\gamma =sup\{\phi (\alpha ,\tau )\mid \tau \in A\}$
and
![]() $\beta =sup\;A$
. We do that by showing that the three conditions given in item 3 of Corollary 7.12 are satisfied.
$\beta =sup\;A$
. We do that by showing that the three conditions given in item 3 of Corollary 7.12 are satisfied.
-
• Let
 $\xi <\alpha $
. Then
$\xi <\alpha $
. Then
 $\phi (\xi ,\gamma )=sup\{\phi (\xi ,\phi (\alpha ,\tau ))\mid \tau \in A\}$
by the induction hypothesis for
$\phi (\xi ,\gamma )=sup\{\phi (\xi ,\phi (\alpha ,\tau ))\mid \tau \in A\}$
by the induction hypothesis for
 $\xi $
. Hence
$\xi $
. Hence
 $\phi (\xi ,\gamma )=\gamma $
by item 1 of Corollary 7.12.
$\phi (\xi ,\gamma )=\gamma $
by item 1 of Corollary 7.12. -
• Let
 $\beta ^\prime <\beta $
. Then there exists
$\beta ^\prime <\beta $
. Then there exists
 $\tau \in A$
such that
$\tau \in A$
such that
 $\beta ^\prime <\tau $
. It follows by item 1 of Proposition 7.11 that
$\beta ^\prime <\tau $
. It follows by item 1 of Proposition 7.11 that
 $\phi (\alpha ,\beta ^\prime )<\phi (\alpha ,\tau )\leq \gamma $
.
$\phi (\alpha ,\beta ^\prime )<\phi (\alpha ,\tau )\leq \gamma $
. -
• Let
 $\gamma ^\prime \!<\!\gamma $
, and suppose that
$\gamma ^\prime \!<\!\gamma $
, and suppose that
 $\phi (\xi ,\gamma ^\prime )=\gamma ^\prime $
for every
$\phi (\xi ,\gamma ^\prime )=\gamma ^\prime $
for every
 $\xi <\alpha $
. We show that there exists
$\xi <\alpha $
. We show that there exists
 $\beta ^\prime \!<\!\beta $
such that
$\beta ^\prime \!<\!\beta $
such that
 $\phi (\alpha ,\beta ^\prime )=\gamma ^\prime $
. Since
$\phi (\alpha ,\beta ^\prime )=\gamma ^\prime $
. Since
 $\gamma ^\prime <\gamma $
, there exists
$\gamma ^\prime <\gamma $
, there exists
 $\beta ^\star \in A$
(and so
$\beta ^\star \in A$
(and so
 $\beta ^\star \leq \beta $
) such that
$\beta ^\star \leq \beta $
) such that
 $\gamma ^\prime <\phi (\alpha ,\beta ^\star )$
. Hence item 2 of Corollary 7.12 implies that there exists
$\gamma ^\prime <\phi (\alpha ,\beta ^\star )$
. Hence item 2 of Corollary 7.12 implies that there exists
 $\beta ^\prime <\beta ^\star \leq \beta $
such that
$\beta ^\prime <\beta ^\star \leq \beta $
such that
 $\phi (\alpha ,\beta ^\prime )=\gamma ^\prime $
.
$\phi (\alpha ,\beta ^\prime )=\gamma ^\prime $
.
7.2
 $\Gamma _0$
and the operation
$\Gamma _0$
and the operation
 $\Gamma $
$\Gamma $
Once the operation
![]() $\phi $
becomes available, it is almost a routine matter to introduce in
$\phi $
becomes available, it is almost a routine matter to introduce in
![]() $\mathbf {PW}$
the operation
$\mathbf {PW}$
the operation
![]() $\Gamma $
as well.
$\Gamma $
as well.
Proposition 7.16.
![]() $\vdash _{\mathbf {PW}}\alpha>0\to (\phi (\alpha ,0)=\alpha \leftrightarrow \forall \xi <\alpha \phi (\xi ,\alpha )=\alpha )$
.
$\vdash _{\mathbf {PW}}\alpha>0\to (\phi (\alpha ,0)=\alpha \leftrightarrow \forall \xi <\alpha \phi (\xi ,\alpha )=\alpha )$
.
Proof The implication from left to right follows from item 1 of Corollary 7.12. Its converse follows from the assumption that
![]() $0<\alpha $
.
$0<\alpha $
.
Theorem 7.17.
![]() $\vdash _{\mathbf {PW}}\forall \alpha \exists \beta (\beta>\alpha \wedge \phi (\beta ,0)=\beta )$
.
$\vdash _{\mathbf {PW}}\forall \alpha \exists \beta (\beta>\alpha \wedge \phi (\beta ,0)=\beta )$
.
Proof Given an ordinal
![]() $\alpha $
, we use Theorem 6.7 to define a function f on
$\alpha $
, we use Theorem 6.7 to define a function f on
![]() $\omega $
by letting
$\omega $
by letting
![]() $f(0)=S(\alpha )$
, and
$f(0)=S(\alpha )$
, and
![]() $f(n+1)=\phi (f(n),0)$
for every
$f(n+1)=\phi (f(n),0)$
for every
![]() $ n\in \omega $
. Then
$ n\in \omega $
. Then
![]() $f(n)\leq f(n+1)$
by Proposition 7.13. Let
$f(n)\leq f(n+1)$
by Proposition 7.13. Let
![]() $\beta =sup\{f(n)\mid n\in \omega \}$
. Obviously,
$\beta =sup\{f(n)\mid n\in \omega \}$
. Obviously,
![]() $\beta>\alpha $
. We show that also
$\beta>\alpha $
. We show that also
![]() $\phi (\beta ,0)=\beta $
. By Proposition 7.16 it suffices to show that
$\phi (\beta ,0)=\beta $
. By Proposition 7.16 it suffices to show that
![]() $\phi (\gamma ,\beta )=\beta $
for every
$\phi (\gamma ,\beta )=\beta $
for every
![]() $\gamma <\beta $
. So let
$\gamma <\beta $
. So let
![]() $\gamma <\beta $
. Then there exists
$\gamma <\beta $
. Then there exists
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $\gamma <f(n)$
for every
$\gamma <f(n)$
for every
![]() $n>k$
. Hence
$n>k$
. Hence
![]() $\phi (\gamma ,f(n))=f(n)$
for every
$\phi (\gamma ,f(n))=f(n)$
for every
![]() $n>k$
by item 1 of Corollary 7.12. It follows by Proposition 7.15 that
$n>k$
by item 1 of Corollary 7.12. It follows by Proposition 7.15 that
![]() $\phi (\gamma ,\beta )=\beta $
.
$\phi (\gamma ,\beta )=\beta $
.
Theorem 7.18.
![]() $\mathbf {PW}$
has an operation
$\mathbf {PW}$
has an operation
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\mathbf {PW}$
proves the following:
$\mathbf {PW}$
proves the following:
-
1.
 $\forall \alpha \forall \beta (\beta>\alpha \to \Gamma (\beta )>\Gamma (\alpha ))$
.
$\forall \alpha \forall \beta (\beta>\alpha \to \Gamma (\beta )>\Gamma (\alpha ))$
. -
2.
 $\forall \alpha \ \phi (\Gamma (\alpha ),0)=\Gamma (\alpha )$
.
$\forall \alpha \ \phi (\Gamma (\alpha ),0)=\Gamma (\alpha )$
. -
3.
 $\forall \alpha \forall \gamma (\Gamma (\alpha )>\gamma \wedge \phi (\gamma ,0)=\gamma \to \exists \beta <\alpha \ \gamma =\Gamma (\beta ))$
.
$\forall \alpha \forall \gamma (\Gamma (\alpha )>\gamma \wedge \phi (\gamma ,0)=\gamma \to \exists \beta <\alpha \ \gamma =\Gamma (\beta ))$
.
Proof Using the basic properties of ordinals, Theorem 7.17 implies that
Therefore it follows from [OpI] that
![]() $\mathbf {PW}$
has an operation G such that
$\mathbf {PW}$
has an operation G such that
We can now use recursion to introduce an operation
![]() $\Gamma $
as follows:
$\Gamma $
as follows:
 $$ \begin{align*}\Gamma(\alpha)=\left\{ \begin{array}{ll} G(0), & \alpha=0,\\ G(\Gamma(\beta)), & \alpha=S(\beta),\\ sup\{\Gamma(\beta)\mid\beta<\alpha\},& \alpha\ \mbox{is a limit ordinal.} \end{array} \right.\end{align*} $$
$$ \begin{align*}\Gamma(\alpha)=\left\{ \begin{array}{ll} G(0), & \alpha=0,\\ G(\Gamma(\beta)), & \alpha=S(\beta),\\ sup\{\Gamma(\beta)\mid\beta<\alpha\},& \alpha\ \mbox{is a limit ordinal.} \end{array} \right.\end{align*} $$
It is obvious that
![]() $\Gamma $
has property 1. To show that
$\Gamma $
has property 1. To show that
![]() $\Gamma $
has property 2, we use an
$\Gamma $
has property 2, we use an
![]() $\in $
-induction on
$\in $
-induction on
![]() $\alpha $
. This is obviously true in case
$\alpha $
. This is obviously true in case
![]() $\alpha =0$
or
$\alpha =0$
or
![]() $\alpha $
is a successor ordinal. So assume that
$\alpha $
is a successor ordinal. So assume that
![]() $\alpha $
is a limit ordinal, By Propositions 7.13 and 7.16, it suffices to show that
$\alpha $
is a limit ordinal, By Propositions 7.13 and 7.16, it suffices to show that
![]() $\phi (\tau ,\Gamma (\alpha ))\leq \Gamma (\alpha )$
for all
$\phi (\tau ,\Gamma (\alpha ))\leq \Gamma (\alpha )$
for all
![]() $\tau <\Gamma (\alpha )$
. So let
$\tau <\Gamma (\alpha )$
. So let
![]() $\tau <\Gamma (\alpha )$
. Since
$\tau <\Gamma (\alpha )$
. Since
![]() $\alpha $
is a limit ordinal, the definition of
$\alpha $
is a limit ordinal, the definition of
![]() $\Gamma (\alpha )$
implies that there is
$\Gamma (\alpha )$
implies that there is
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $\tau <\Gamma (\beta )$
. By induction hypothesis and Corollary 7.12, for every such
$\tau <\Gamma (\beta )$
. By induction hypothesis and Corollary 7.12, for every such
![]() $\beta $
it holds that
$\beta $
it holds that
![]() $\phi (\tau ,\Gamma (\beta ))=\Gamma (\beta )$
and so
$\phi (\tau ,\Gamma (\beta ))=\Gamma (\beta )$
and so
![]() $\phi (\tau ,\Gamma (\beta ))< \Gamma (\alpha )$
. By Proposition 7.15, this implies that
$\phi (\tau ,\Gamma (\beta ))< \Gamma (\alpha )$
. By Proposition 7.15, this implies that
![]() $\phi (\tau ,\Gamma (\alpha ))\leq \Gamma (\alpha )$
.
$\phi (\tau ,\Gamma (\alpha ))\leq \Gamma (\alpha )$
.
Finally, we prove that
![]() $\Gamma $
has property 3 by an
$\Gamma $
has property 3 by an
![]() $\in $
-induction on
$\in $
-induction on
![]() $\alpha $
. So suppose that
$\alpha $
. So suppose that
![]() $\Gamma (\alpha )>\gamma $
and
$\Gamma (\alpha )>\gamma $
and
![]() $\phi (\gamma ,0)=\gamma $
. There are three cases to consider:
$\phi (\gamma ,0)=\gamma $
. There are three cases to consider:
-
• The case
 $\alpha =0$
is trivial, since by definition of G, there is no
$\alpha =0$
is trivial, since by definition of G, there is no
 $\gamma $
such that
$\gamma $
such that
 $\Gamma (0)>\gamma $
and
$\Gamma (0)>\gamma $
and
 $\phi (\gamma ,0)=\gamma $
.
$\phi (\gamma ,0)=\gamma $
. -
• Suppose that
 $\alpha =S(\xi )$
for some
$\alpha =S(\xi )$
for some
 $\xi $
. Then
$\xi $
. Then
 $\Gamma (\alpha )=G(\Gamma (\xi ))$
. It follows that
$\Gamma (\alpha )=G(\Gamma (\xi ))$
. It follows that
 $\gamma <G(\Gamma (\xi ))$
. By the properties of G, this implies that
$\gamma <G(\Gamma (\xi ))$
. By the properties of G, this implies that
 $\gamma \leq \Gamma (\xi )$
. If
$\gamma \leq \Gamma (\xi )$
. If
 $\gamma =\Gamma (\xi )$
we are done. Otherwise we apply the induction hypothesis to
$\gamma =\Gamma (\xi )$
we are done. Otherwise we apply the induction hypothesis to
 $\xi $
, and get
$\xi $
, and get
 $\beta <\xi <\alpha $
such that
$\beta <\xi <\alpha $
such that
 $\gamma =\Gamma (\beta )$
.
$\gamma =\Gamma (\beta )$
. -
• Suppose that
 $\alpha $
is a limit ordinal. Then by definition of
$\alpha $
is a limit ordinal. Then by definition of
 $\Gamma $
,
$\Gamma $
,
 $\gamma <\Gamma (\alpha )$
implies that
$\gamma <\Gamma (\alpha )$
implies that
 $\gamma <\Gamma (\xi )$
for some
$\gamma <\Gamma (\xi )$
for some
 $\xi <\alpha $
. By applying the induction hypothesis to
$\xi <\alpha $
. By applying the induction hypothesis to
 $\xi $
we get
$\xi $
we get
 $\beta <\xi <\alpha $
such that
$\beta <\xi <\alpha $
such that
 $\gamma =\Gamma (\beta )$
.
$\gamma =\Gamma (\beta )$
.
Corollary 7.19.
![]() $\vdash _{\mathbf {PW}} \phi (\gamma ,0)=\gamma \to \exists \beta (\gamma =\Gamma (\beta )).$
$\vdash _{\mathbf {PW}} \phi (\gamma ,0)=\gamma \to \exists \beta (\gamma =\Gamma (\beta )).$
Proof Together with the first item of Theorem 7.18, Proposition 6.9 implies that
![]() $\gamma \leq \Gamma (\gamma )<\Gamma (S(\gamma ))$
. Hence the claim follows from item 3 of that theorem.
$\gamma \leq \Gamma (\gamma )<\Gamma (S(\gamma ))$
. Hence the claim follows from item 3 of that theorem.
Corollary 7.20. Feferman–Schütte’s ordinal
![]() $\Gamma (0)$
(usually denoted
$\Gamma (0)$
(usually denoted
![]() $\Gamma _0$
) is definable by a term of
$\Gamma _0$
) is definable by a term of
![]() $\mathbf {PW}$
. So are much bigger ordinals, like
$\mathbf {PW}$
. So are much bigger ordinals, like
![]() $\Gamma (\Gamma _0)$
.
$\Gamma (\Gamma _0)$
.
Note 7.21. It is not difficult to define in
![]() $\mathbf {PW}$
a relation R on
$\mathbf {PW}$
a relation R on
![]() $\omega $
such that
$\omega $
such that
![]() $\mathbf {PW}$
proves that
$\mathbf {PW}$
proves that
![]() $\langle \omega ,R \rangle $
is isomorphic to
$\langle \omega ,R \rangle $
is isomorphic to
![]() $\langle \Gamma _0,\in \rangle $
. This can be done, e.g., by using the recursive well-ordering of the natural numbers which is constructed in [Reference Schütte43] (with the help of notations for the ordinals smaller than
$\langle \Gamma _0,\in \rangle $
. This can be done, e.g., by using the recursive well-ordering of the natural numbers which is constructed in [Reference Schütte43] (with the help of notations for the ordinals smaller than
![]() $\Gamma _0$
).
$\Gamma _0$
).
8 Conclusion and further research
As recalled by Feferman in [Reference Feferman and Shapiro24], Kreisel criticized in [Reference Kreisel and Kino31] existing proof theory for “the lack of a clear and convincing analysis of the choice of methods of proof,” and took as his ultimate aim “the discovery of objective criteria for such a choice”. Following ideas of Poincaré and Weyl, in this paper we have done exactly this for predicative set theory, using invariance of definitions and statements as our main criterion. What is more, we have shown that the power of predicative reasoning goes well beyond the accepted
![]() $\Gamma _0$
limit given to it by Feferman and Schütte.
$\Gamma _0$
limit given to it by Feferman and Schütte.
At this point it should be emphasized that we are not claiming that the predicative system
![]() $\mathbf {PW}$
which is developed in this paper is in any way complete for predicative set theory. Given Weyl’s views about the open-ended nature of predicativity (which are adopted and followed in this paper), it is hard to believe that such a complete system exists—even from the point of view of a Platonist who tries to determine “from the outside” the extension and limit of predicative reasoning (as Feferman explicitly tried to do in [Reference Feferman15]). Thus, in this paper we have deliberately confined ourselves only to methods that were accepted in one way or another by Feferman in some of his systems. However, there is no reason to continue to do so in future predicative extensions of
$\mathbf {PW}$
which is developed in this paper is in any way complete for predicative set theory. Given Weyl’s views about the open-ended nature of predicativity (which are adopted and followed in this paper), it is hard to believe that such a complete system exists—even from the point of view of a Platonist who tries to determine “from the outside” the extension and limit of predicative reasoning (as Feferman explicitly tried to do in [Reference Feferman15]). Thus, in this paper we have deliberately confined ourselves only to methods that were accepted in one way or another by Feferman in some of his systems. However, there is no reason to continue to do so in future predicative extensions of
![]() $\mathbf {PW}$
. One obvious direction here is to investigate what sorts of inductive definitions of operations and predicates are predicatively acceptable. (Note that
$\mathbf {PW}$
. One obvious direction here is to investigate what sorts of inductive definitions of operations and predicates are predicatively acceptable. (Note that
![]() $\mathbf {PW}$
allows to introduce new predicate symbols only via explicit definitions, but there is no reason to forbid predicative implicit definitions of predicates, as long as the invariance condition is observed.) According to the principles which guide us in this work, such a definition should be acceptable whenever it uniquely and invariantly determines in our framework the predicate or operation which it defines. This mean that an inductive definition which uniquely determines only some minimal predicate or operation satisfying certain conditions is not acceptable. In contrast, an example of an implicit definition of a predicate that should be acceptable is the following inductive characterization of
$\mathbf {PW}$
allows to introduce new predicate symbols only via explicit definitions, but there is no reason to forbid predicative implicit definitions of predicates, as long as the invariance condition is observed.) According to the principles which guide us in this work, such a definition should be acceptable whenever it uniquely and invariantly determines in our framework the predicate or operation which it defines. This mean that an inductive definition which uniquely determines only some minimal predicate or operation satisfying certain conditions is not acceptable. In contrast, an example of an implicit definition of a predicate that should be acceptable is the following inductive characterization of
![]() $\in ^\star $
, the transitive closure of
$\in ^\star $
, the transitive closure of
![]() $\in $
:
$\in $
:
![]() $y\in ^\star x\leftrightarrow y\in x \vee \exists z\in x.y\in ^\star z$
.
$y\in ^\star x\leftrightarrow y\in x \vee \exists z\in x.y\in ^\star z$
.
Another important goal for further research is to develop mathematics in
![]() $\mathbf {PW}$
(or in a predicative extension of it) in a way which is as natural as possible. Significant work in this direction has started in [Reference Avron and Cohen7], and is extended and corrected in the Ph.D thesis of Nissan Levy [Reference Levi32] (see also [Reference Levi and Avron33] for a part of his work).
$\mathbf {PW}$
(or in a predicative extension of it) in a way which is as natural as possible. Significant work in this direction has started in [Reference Avron and Cohen7], and is extended and corrected in the Ph.D thesis of Nissan Levy [Reference Levi32] (see also [Reference Levi and Avron33] for a part of his work).
Finally, two interesting technical questions concerning
![]() $\mathbf {PW}$
, which we have not tried to answer yet, are:
$\mathbf {PW}$
, which we have not tried to answer yet, are:
-
• What is the proof-theoretic ordinal of
 $\mathbf {PW}$
?
$\mathbf {PW}$
? -
• What is the minimal ordinal (from a platonistic point of view) that is not definable by a term of
 $\mathbf {PW}$
? (Given a set theory S, we call such an ordinal the set-theoretical ordinal of S.)
$\mathbf {PW}$
? (Given a set theory S, we call such an ordinal the set-theoretical ordinal of S.)
Acknowledgment
I am grateful to Laura Crosilla, Jerhard Jäger, Nik Weaver, and an anonymous referee for helpful comments on the first draft of this paper.
Funding
This research has been supported by Len Blavatnik and the Blavatnik Family Foundation.