Hostname: page-component-6587cd75c8-mppm8 Total loading time: 0 Render date: 2025-04-23T23:53:42.341Z Has data issue: false hasContentIssue false
  • English
  • Français

A ONE-PAGE PROOF OF A THEOREM OF BELEZNAY

Part of: Computability and recursion theory Set theory Ordered sets

Published online by Cambridge University Press:  18 March 2025

JUAN P. AGUILERA  and
MARTINA IANNELLA
JUAN P. AGUILERA
Affiliation:
DEPARTMENT OF DISCRETE MATHEMATICS AND GEOMETRY TU WIEN WIEDNER HAUPTSTR 8–10, 1040 VIENNA AUSTRIA E-mail: [email protected] E-mail: [email protected]
MARTINA IANNELLA
Affiliation:
DEPARTMENT OF DISCRETE MATHEMATICS AND GEOMETRY TU WIEN WIEDNER HAUPTSTR 8–10, 1040 VIENNA AUSTRIA E-mail: [email protected] E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a short proof of a theorem of Beleznay asserting that the set $L2$ of reals coding linear orders of the form 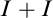$I + I$ is complete analytic.

Keywords

descriptive set theorylinear orderanalytic setHarrison order

MSC classification

Primary: 03E15: Descriptive set theory 03D55: Hierarchies 06A05: Total order
Type
Article
Information
Bulletin of Symbolic Logic , Volume 30 , Issue 4 , December 2024 , pp. 536 - 537
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Becker, H., Descriptive set theoretic phenomena in analysis and topology , Set Theory of the Continuum (Judah, H., Just, W., and Woodin, H., editors), Springer-Verlag, New York, 1992, pp. 1–25.Google Scholar
Beleznay, F., The complexity of the collection of countable linear orders of the form $I+I$ . Journal of Symbolic Logic , vol. 64 (1999), pp. 1519–1526.CrossRefGoogle Scholar
Harrison, J., Recursive pseudo-well-orderings . Transactions of the American Mathematical Society , vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
Humke, P. D. and Laczkovich, M., The Borel structure of iterates of continuous functions . Proceedings of the Edinburgh Mathematical Society , vol. 32 (1989), pp. 483–494.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory , Springer-Verlag, New York, 1994.Google Scholar
Marcone, A. and Montalbán, A., The Veblen function for computability theorists . Journal of Symbolic Logic , 76 (2011), pp. 575–602.CrossRefGoogle Scholar
Montalbán, A., Computable Structure Theory II: Beyond the Arithmetic . Book draft.Google Scholar