Published online by Cambridge University Press: 26 July 2021
We ask, when is a property of a model a logical property? According to the so-called Tarski–Sher criterion this is the case when the property is preserved by isomorphisms. We relate this to model-theoretic characteristics of abstract logics in which the model class is definable. This results in a graded concept of logicality in the terminology of Sagi [46]. We investigate which characteristics of logics, such as variants of the Löwenheim–Skolem theorem, Completeness theorem, and absoluteness, are relevant from the logicality point of view, continuing earlier work by Bonnay, Feferman, and Sagi. We suggest that a logic is the more logical the closer it is to first order logic. We also offer a refinement of the result of McGee that logical properties of models can be expressed in 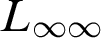 $L_{\infty \infty }$
if the expression is allowed to depend on the cardinality of the model, based on replacing
$L_{\infty \infty }$
if the expression is allowed to depend on the cardinality of the model, based on replacing 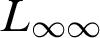 $L_{\infty \infty }$
by a “tamer” logic.
$L_{\infty \infty }$
by a “tamer” logic.