Article contents
Hyperclassical Logic (A.K.A. If Logic) and its Implications for Logical Theory
Published online by Cambridge University Press: 15 January 2014
Extract
Let us assume that you are entrusted by UNESCO with an important task. You are asked to devise a universal logical language, a Begriffsschrift in Frege's sense, which is to serve the purposes of science, business and everyday life. What requirements should such a “conceptual notation” satisfy? There are undoubtedly many relevant desiderata, but here I am focusing on one unmistakable one. In order to be a viable lingua universalis, your language must in any case be capable of representing any possible configuration of dependence and independence between different variables. For if such a configuration is possible in principle, there is no guarantee that it might not one day show up among the natural, human or social phenomena we have to study.
But how are dependencies and independencies between variables expressed in our familiar logical notation? Every logician worth his or her truth-table knows the answer. Dependencies between two variables are expressed by dependencies between the quantifiers to which they are bound. For instance, in

the variable y depends on x, while in
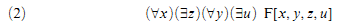
z depends on x but not on y, while u depends on both x and y.
But how is the dependence of a quantifier on another one expressed in familiar logical languages? Obviously by occurring in its scope, indicated by the pair of parentheses following it (cf. here Hintikka [1997]). But the nesting of scopes is a transitive and antisymmetrical relation which allows branching only in one direction. Hence other kinds of structures of dependence and independence between variables are not representable in the received logical notation. Such previously inexpressible structures form the subject matter of what has been referred to as independence-friendly (IF) logic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 15
- Cited by


