No CrossRef data available.
Expansions and Neostability in Model Theory
Published online by Cambridge University Press: 16 September 2021
Abstract
This thesis is concerned with the expansions of algebraic structures and their fit in Shelah’s classification landscape.
The first part deals with the expansion of a theory by a random predicate for a substructure model of a reduct of the theory. Let T be a theory in a language 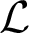 $\mathcal {L}$
. Let
$\mathcal {L}$
. Let 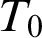 $T_0$
be a reduct of T. Let
$T_0$
be a reduct of T. Let 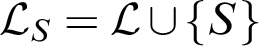 $\mathcal {L}_S = \mathcal {L}\cup \{S\}$
, for S a new unary predicate symbol, and
$\mathcal {L}_S = \mathcal {L}\cup \{S\}$
, for S a new unary predicate symbol, and 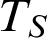 $T_S$
be the
$T_S$
be the 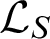 $\mathcal {L}_S$
-theory that axiomatises the following structures:
$\mathcal {L}_S$
-theory that axiomatises the following structures: 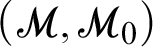 $(\mathscr {M},\mathscr {M}_0)$
consist of a model
$(\mathscr {M},\mathscr {M}_0)$
consist of a model 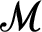 $\mathscr {M}$
of T and S is a predicate for a model
$\mathscr {M}$
of T and S is a predicate for a model  $\mathscr {M}_0$
of
$\mathscr {M}_0$
of 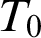 $T_0$
which is a substructure of
$T_0$
which is a substructure of 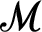 $\mathscr {M}$
. We present a setting for the existence of a model-companion
$\mathscr {M}$
. We present a setting for the existence of a model-companion 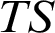 $TS$
of
$TS$
of 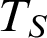 $T_S$
. As a consequence, we obtain the existence of the model-companion of the following theories, for
$T_S$
. As a consequence, we obtain the existence of the model-companion of the following theories, for 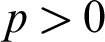 $p>0$
a prime number:
$p>0$
a prime number:
•
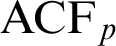 $\mathrm {ACF}_p$
,
$\mathrm {ACF}_p$
, 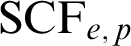 $\mathrm {SCF}_{e,p}$
,
$\mathrm {SCF}_{e,p}$
, 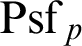 $\mathrm {Psf}_p$
,
$\mathrm {Psf}_p$
, 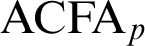 $\mathrm {ACFA}_p$
,
$\mathrm {ACFA}_p$
, 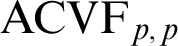 $\mathrm {ACVF}_{p,p}$
in appropriate languages expanded by arbitrarily many predicates for additive subgroups;
$\mathrm {ACVF}_{p,p}$
in appropriate languages expanded by arbitrarily many predicates for additive subgroups;•
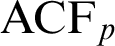 $\mathrm {ACF}_p$
,
$\mathrm {ACF}_p$
, 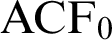 $\mathrm {ACF}_0$
in the language of rings expanded by a single predicate for a multiplicative subgroup;
$\mathrm {ACF}_0$
in the language of rings expanded by a single predicate for a multiplicative subgroup;•
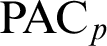 $\mathrm {PAC}_p$
-fields, in an appropriate language expanded by arbitrarily many predicates for additive subgroups.
$\mathrm {PAC}_p$
-fields, in an appropriate language expanded by arbitrarily many predicates for additive subgroups.
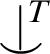 in T, we define independence relations in
in T, we define independence relations in 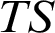 $TS$
and identify which properties of
$TS$
and identify which properties of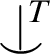 are transferred to those new independence relations in
are transferred to those new independence relations in 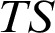 $TS$
, and under which conditions. This allows us to exhibit hypotheses under which the expansion from T to
$TS$
, and under which conditions. This allows us to exhibit hypotheses under which the expansion from T to 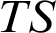 $TS$
preserves
$TS$
preserves 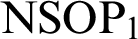 $\mathrm {NSOP}_{1}$
, simplicity, or stability. In particular, under some technical hypothesis on T, we may draw the following picture (the left column implies the right column):
$\mathrm {NSOP}_{1}$
, simplicity, or stability. In particular, under some technical hypothesis on T, we may draw the following picture (the left column implies the right column):
Configuration 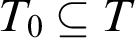 $T_0\subseteq T$
$T_0\subseteq T$
| Generic expansion 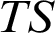 $TS$
$TS$
|
|---|---|
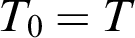 $T_0 = T$
$T_0 = T$
| Preserves stability |
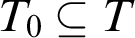 $T_0\subseteq T$
$T_0\subseteq T$
| Preserves 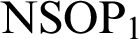 $\mathrm {NSOP}_{1}$
$\mathrm {NSOP}_{1}$
|
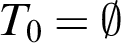 $T_0 = \emptyset $
$T_0 = \emptyset $
| Preserves simplicity |
In particular, this construction produces new examples of 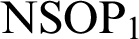 $\mathrm {NSOP}_{1}$
not simple theories, and we study in depth a particular example: the expansion of an algebraically closed field of positive characteristic by a generic additive subgroup. We give a full description of imaginaries, forking, and Kim-forking in this example.
$\mathrm {NSOP}_{1}$
not simple theories, and we study in depth a particular example: the expansion of an algebraically closed field of positive characteristic by a generic additive subgroup. We give a full description of imaginaries, forking, and Kim-forking in this example.
The second part studies expansions of the group of integers by p-adic valuations. We prove quantifier elimination in a natural language and compute the dp-rank of these expansions: it equals the number of independent p-adic valuations considered. Thus, the expansion of the integers by one p-adic valuation is a new dp-minimal expansion of the group of integers. Finally, we prove that the latter expansion does not admit intermediate structures: any definable set in the expansion is either definable in the group structure or is able to “reconstruct” the valuation using only the group operation.
Abstract prepared by Christian d’Elbée.
E-mail: [email protected]
Keywords
MSC classification
- Type
- Thesis Abstracts
- Information
- Copyright
- © Association for Symbolic Logic 2021
Footnotes
Supervised by Thomas Blossier and Zoé Chatzidakis.



