Published online by Cambridge University Press: 05 January 2021
We introduce a tool for analysing models of 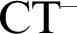 $\text {CT}^-$
, the compositional truth theory over Peano Arithmetic. We present a new proof of Lachlan’s theorem that the arithmetical part of models of
$\text {CT}^-$
, the compositional truth theory over Peano Arithmetic. We present a new proof of Lachlan’s theorem that the arithmetical part of models of 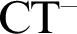 $\text {CT}^-$
are recursively saturated. We also use this tool to provide a new proof of theorem from [8] that all models of
$\text {CT}^-$
are recursively saturated. We also use this tool to provide a new proof of theorem from [8] that all models of 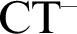 $\text {CT}^-$
carry a partial inductive truth predicate. Finally, we construct a partial truth predicate defined for a set of formulae whose syntactic depth forms a nonstandard cut which cannot be extended to a full truth predicate satisfying
$\text {CT}^-$
carry a partial inductive truth predicate. Finally, we construct a partial truth predicate defined for a set of formulae whose syntactic depth forms a nonstandard cut which cannot be extended to a full truth predicate satisfying 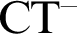 $\text {CT}^-$
.
$\text {CT}^-$
.