Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T15:03:41.997Z Has data issue: false hasContentIssue false
  • English
  • Français

The Complexity of Orbits of Computably Enumerable Sets

Published online by Cambridge University Press:  15 January 2014

Peter A. Cholak ,
Rodney Downey  and
Leo A. Harrington
Peter A. Cholak
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556-5683, USAE-mail: [email protected]: http://www.nd.edu/~cholak
Rodney Downey
Affiliation:
School of Mathematics, Statistics and Computer Science, Victoria University, P.O. BOX 600, Wellington, New ZealandE-mail: [email protected] , URL: http://www.mcs.vuw.ac.nz/~downey
Leo A. Harrington
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

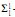The goal of this paper is to announce there is a single orbit of the c.e. sets with inclusion, ε, such that the question of membership in this orbit is complete. This result and proof have a number of nice corollaries: the Scott rank of ε is 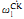+ 1; not all orbits are elementarily definable; there is no arithmetic description of all orbits of ε; for all finite α ≥ 9, there is a properly 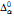orbit (from the proof).

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 14 , Issue 1 , March 2008 , pp. 69 - 87
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ash, C. J. and Knight, J., Computable structures and the hyperarithmetical hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
[2] Cholak, Peter, Automorphisms of the lattice of recursively enumerable sets, Ph.D. thesis, University of Wisconsin, 1991.Google Scholar
[3] Cholak, Peter, The translation theorem, Archive for Mathematical Logic, vol. 33 (1994), pp. 87–108.Google Scholar
[4] Cholak, Peter, Automorphisms of the lattice of recursively enumerable sets, Memoirs of the American Mathematical Society, vol. 113 (1995), no. 541.Google Scholar
[5] Cholak, Peter, The Computably Enumerable Sets: the Past, the Present and the Future, Theory and Applications of Models of Computation, 2006, Beijing China, Slides can be found at http://www.nd.edu/~cholak, 2006.Google Scholar
[6] Cholak, Peter and Downey, Rod, Invariance and noninvariance in the lattice of classes, Journal of the London Mathematical Society. Second Series, vol. 70 (2004), no. 3, pp. 735–749.Google Scholar
[7] Cholak, Peter, Downey, Rod, and Harrington, Leo, On the Orbits of Computable Enumerable Sets, Submitted. math.LO/0607264.Google Scholar
[8] Cholak, Peter, Downey, Rod, and Herrmann, Eberhard, Some orbits for ε, Annals of Pure and Applied Logic, vol. 107 (2001), no. 1–3, pp. 193–226.CrossRefGoogle Scholar
[9] Cholak, Peter, Downey, Rod, and Stob, Michael, Automorphisms of the lattice of recursively enumerable sets: Promptly simple sets, Transactions of the American Mathematical Society, vol. 332 (1992), pp. 555–570.CrossRefGoogle Scholar
[10] Cholak, Peter and Harrington, Leo, Extension theorems, orbits, and automorphisms of the computably enumerable sets, To appear in Transactions of the American Mathematical Society. Final version as of 8/31/2005. math.LO/0408279.Google Scholar
[11] Cholak, Peter and Harrington, Leo, Definable encodings in the computably enumerable sets, this Bulletin, vol. 6 (2000), no. 2, pp. 185–196, A copy can be found at http://www.nd.edu/~cholak.Google Scholar
[12] Cholak, Peter and Harrington, Leo, On the definability of the double jump in the computably enumerable sets, Journal of Mathematical Logic, vol. 2 (2002), no. 2, pp. 261–296.Google Scholar
[13] Cholak, Peter and Harrington, Leo, Isomorphisms of splits of computably enumerable sets, The Journal of Symbolic Logic, vol. 68 (2003), no. 3, pp. 1044–1064.CrossRefGoogle Scholar
[14] Downey, Rod and Harrington, Leo, There is no fat orbit, Annals of Pure and Applied Logic, vol. 80 (1996), no. 3, pp. 277–289.Google Scholar
[15] Downey, Rod and Montalbalán, Antonio, Slender classes, Submitted, 2006.Google Scholar
[16] Downey, Rod and Stob, Michael, Jumps of hemimaximal sets, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 37 (1991), pp. 113–120.Google Scholar
[17] Downey, Rod and Stob, Michael, Automorphisms of the lattice of recursively enumerable sets: Orbits, Advances in Mathematics, vol. 92 (1992), pp. 237–265.Google Scholar
[18] Friedberg, R. M., A criterion for completeness of degrees of unsolvability, The Journal of Symbolic Logic, vol. 22 (1957), pp. 159–160.Google Scholar
[19] Goncharov, Sergey S., Harizanov, Valentina S., Knight, Julia F., and Shore, Richard A., relations and paths through , The Journal of Symbolic Logic, vol. 69 (2004), no. 2, pp. 585–611.CrossRefGoogle Scholar
[20] Harrington, Leo and Soare, Robert I., Post's program and incomplete recursively enumerable sets, Proceedings of the National Academy of Sciences of the United States of America, vol. 88 (1991), pp. 10242–10246.Google Scholar
[21] Harrington, Leo and Soare, Robert I., Definability, automorphisms, and dynamic properties of computably enumerable sets, this Bulletin, vol. 2 (1996), no. 2, pp. 199–213.Google Scholar
[22] Harrington, Leo and Soare, Robert I., The -automorphism method and noninvariant classes of degrees, Journal of the American Mathematical Society, vol. 9 (1996), no. 3, pp. 617–666.CrossRefGoogle Scholar
[23] Harrington, Leo and Soare, Robert I., Codable sets and orbits of computably enumerable sets, The Journal of Symbolic Logic, vol. 63 (1998), no. 1, pp. 1–28.Google Scholar
[24] Kleene, Stephen C. and Post, Emil L., The upper semi-lattice of degrees of recursive unsolvability, Annals of Mathematics (2), vol. 59 (1954), pp. 379–407.Google Scholar
[25] Lachlan, Alistair H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.Google Scholar
[26] Lerman, Manuel and Soare, Robert I., d-simple sets, small sets, and degree classes, Pacific Journal of Mathematics, vol. 87 (1980), no. 1, pp. 135–155.Google Scholar
[27] Maass, W., On the orbit of hyperhypersimple sets, The Journal of Symbolic Logic, vol. 49 (1984), pp. 51–62.Google Scholar
[28] Maass, W. and Stob, M., The intervals of the lattice of recursively enumerable sets determined by major subsets, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.Google Scholar
[29] Marchenkov, S. S., A class of incomplete sets, Mathematische Zeitschrift, vol. 20 (1976), pp. 473–487.Google Scholar
[30] Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.Google Scholar
[31] Muchnik, A. A., On the unsolvability of the problem of reducibility in the theory of algorithms, Doklady Akademii Nauk SSSR, vol. N. S. 108 (1956), pp. 194–197.Google Scholar
[32] Post, Emil L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.Google Scholar
[33] Slaman, Theodore A. and Woodin, W. Hugh, Personal communication, 1989.Google Scholar
[34] Soare, Robert I., Automorphisms of the lattice of recursively enumerable sets, Bulletin of the American Mathematical Society, vol. 80 (1974), pp. 53–58.Google Scholar
[35] Soare, Robert I., Automorphisms of the lattice of recursively enumerable sets I: maximal sets, Annals of Mathematics (2), vol. 100 (1974), pp. 80–120.CrossRefGoogle Scholar
[36] Turing, Alan M., Systems of logic based on ordinals, Journal of the London Mathematical Society. Third Series, vol. 45 (1939), pp. 161–228.Google Scholar
[37] Weber, Rebecca, A definable relation between c.e. sets and ideals, Ph.D. thesis, University of Notre Dame, 2004.Google Scholar
[38] Soare, Robert I., Invariance in ε*. and εΠ , Transactions of the American Mathematical Society, vol. 358 (2006), no. 7, pp. 3023–3059 (electronic).Google Scholar
[39] White, Walker M., Characterizations for computable structures, Ph.D. thesis, Cornell University, Ithaca, NY, USA, 2000.Google Scholar