Article contents
Arguments for the Continuity Principle
Published online by Cambridge University Press: 15 January 2014
Extract
There are two principles that lend Brouwer's mathematics the extra power beyond arithmetic. Both are presented in Brouwer's writings with little or no argument. One, the principle of bar induction, will not concern us here. The other, the continuity principle for numbers, occurs for the first time in print in [4]. It is formulated and immediately applied to show that the set of numerical choice sequences is not enumerable. In fact, the idea of the continuity property can be dated fairly precisely, it is to be found in the margin of Brouwer's notes for his course on Pointset Theory of 1915/16. The course was repeated in 1916/17 and he must have inserted his first formulation of the continuity principle in the fall of 1916 as new material right at the beginning of the course.
In modern language, the principle reads

where α and β range over choice sequences of natural numbers, m and x over natural numbers, and 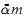 stands for ⟨α(0), α(1), …, α(m − 1)⟩, the initial segment of α of length m.
stands for ⟨α(0), α(1), …, α(m − 1)⟩, the initial segment of α of length m.
An immediate consequence of WC-N is that all full functions are continuous, and, as a corollary, that the continuum is unsplittable [28]. Note that WC-N is incompatible with Church's thesis, [22], section 4.6.
After Brouwer asserted WC-N, Troelstra was the first to ask in print for a conceptual motivation, but he remained an exception; most authors followed Brouwer by simply asserting it, cf. [18].
Let us note first that in one particular case the principle is obvious indeed, namely in the case of the lawless sequences. The notion of lawless sequence surfaced fairly late in the history of intuitionism. Kreisel introduced it in [17] for metamathematical purposes. There is a letter from Brouwer to Heyting in which the phenomenon also occurs [7]. This is an important and interesting fact since it is (probably) the only time that Brouwer made use of a possibility expressly stipulated in, e.g., [5], see below.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 24
- Cited by


