Published online by Cambridge University Press: 15 January 2014
The class of all recursive functions fails to possess a natural hierarchical structure, generated predicatively from “within”. On the other hand, many (proof-theoretically significant) sub-recursive classes do. This paper attempts to measure the limit of predicative generation in this context, by classifying and characterizing those (predictably terminating) recursive functions which can be successively defined according to an autonomy condition of the form: allow recursions only over well-orderings which have already been “coded” at previous levels. The question is: how can a recursion code a well-ordering? The answer lies in Girard's theory of dilators, but is reworked here in a quite different and simplified framework specific to our purpose. The “accessible” recursive functions thus generated turn out to be those provably recursive in (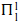 –CA)0.
–CA)0.