Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-29T00:55:39.289Z Has data issue: false hasContentIssue false
  • English
  • Français

VERY LARGE SET AXIOMS OVER CONSTRUCTIVE SET THEORIES

Part of: Set theory

Published online by Cambridge University Press:  26 February 2024

HANUL JEON Open the ORCID record for HANUL JEON [Opens in a new window]  and
RICHARD MATTHEWS
HANUL JEON
Affiliation:
DEPARTMENT OF MATHEMATICS CORNELL UNIVERSITY ITHACA, NY 14853, USA E-mail: [email protected] URL: https://hanuljeon95.github.io
RICHARD MATTHEWS
Affiliation:
LABORATOIRE D’ALGORITHMIQUE, COMPLEXITÉ ET LOGIQUE UNIVERSITÉ PARIS-EST CRÉTEIL CRÉTEIL F-94010, FRANCE E-mail: [email protected] URL: https://richardmatthewslogic.github.io/
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate large set axioms defined in terms of elementary embeddings over constructive set theories, focusing on 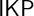$\mathsf {IKP}$ and 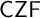$\mathsf {CZF}$. Most previously studied large set axioms, notably, the constructive analogues of large cardinals below 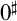$0^\sharp $, have proof-theoretic strength weaker than full Second-Order Arithmetic. On the other hand, the situation is dramatically different for those defined via elementary embeddings. We show that by adding to 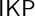$\mathsf {IKP}$ the basic properties of an elementary embedding 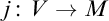$j\colon V\to M$ for 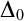$\Delta _0$-formulas, which we will denote by 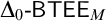$\Delta _0\text {-}\mathsf {BTEE}_M$, we obtain the consistency of 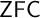$\mathsf {ZFC}$ and more. We will also see that the consistency strength of a Reinhardt set exceeds that of 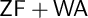$\mathsf {ZF+WA}$. Furthermore, we will define super Reinhardt sets and $\mathsf {TR}$, which is a constructive analogue of V being totally Reinhardt, and prove that their proof-theoretic strength exceeds that of $\mathsf {ZF}$ with choiceless large cardinals.

Keywords

constructive set theorylarge set axiomselementary embeddingconsistency strength

MSC classification

Primary: 03E70: Nonclassical and second-order set theories
Secondary: 03E55: Large cardinals
Type
Article
Information
Bulletin of Symbolic Logic , Volume 30 , Issue 4 , December 2024 , pp. 455 - 535
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aczel, P., The type theoretic interpretation of constructive set theory , Logic Colloquium ’77 (Proc. Conf., Wrocław, 1977) , Studies in Logic and the Foundations of Mathematics, vol. 96, North-Holland, Amsterdam–New York, 1978, pp. 55–66.Google Scholar
Aczel, P., The type theoretic interpretation of constructive set theory: Choice principles , The L. E. J. Brouwer Centenary Symposium (Noordwijkerhout, 1981) , Studies in Logic and the Foundations of Mathematics, vol. 110, North-Holland, Amsterdam, 1982, pp. 1–40.Google Scholar
Aczel, P., The type theoretic interpretation of constructive set theory: Inductive definitions , Logic, Methodology and Philosophy of Science, VII (Salzburg, 1983) , Studies in Logic and the Foundations of Mathematics, vol. 114, North-Holland, Amsterdam, 1986, pp. 17–49.Google Scholar
Aczel, P., The relation reflection scheme . Mathematical Logic Quarterly , vol. 54 (2008), no. 1, pp. 5–11.Google Scholar
Aczel, P. and Rathjen, M., Notes on constructive set theory. Technical report no. 40, Mittag-Leffler, 2001.Google Scholar
Aczel, P. and Rathjen, M., CST book draft, 2010.Google Scholar
Apter, A. W. and Sargsyan, G., Jonsson-like partition relations and $j:V\to V$ . The Journal of Symbolic Logic , vol. 69 (2004), no. 4, pp. 1267–1281.Google Scholar
Arai, T., Ordinal Analysis with an Introduction to Proof Theory , Springer, Singapore, 2020.Google Scholar
Avigad, J., Interpreting classical theories in constructive ones . The Journal of Symbolic Logic , vol. 65 (2000), no. 4, pp. 1785–1812.Google Scholar
Bagaria, J., Koellner, P., and Woodin, W. H., Large cardinals beyond choice, this Journal, vol. 25 (2019), no. 3, pp. 283–318.Google Scholar
Bell, J. L., Intuitionistic Set Theory , College Publications, London, 2014.Google Scholar
Corazza, P., The wholeness axiom and laver sequences . Annals of Pure and Applied Logic , vol. 105 (2000), nos. 1–3, pp. 157–260.Google Scholar
Corazza, P., The spectrum of elementary embeddings $j:V\to V$ . Annals of Pure and Applied Logic , vol. 139 (2006), nos. 1–3, pp. 327–399.Google Scholar
Crosilla, M. L., Realizability models for constructive set theories with restricted induction principles , Ph.D. thesis, University of Leeds, 2000.Google Scholar
Friedman, H., The consistency of classical set theory relative to a set theory with intuitionistic logic . The Journal of Symbolic Logic , vol. 38 (1973), no. 2, pp. 315–319.Google Scholar
Friedman, H. and Ščedrov, A., Large sets in intuitionistic set theory . Annals of Pure and Applied Logic , vol. 27 (1984), no. 1, pp. 1–24.Google Scholar
Friedman, S.-D., Gitman, V., and Kanovei, V., A model of second-order arithmetic satisfying AC but not DC . Journal of Mathematical Logic , vol. 19 (2019), no. 1, p. 1850013.Google Scholar
Gaifman, H., Elementary embeddings of models of set-theory and certain subtheories , Axiomatic Set Theory (Proc. Sympos. Pure Math., Vol. XIII, Part II, Univ. California, Los Angeles, Calif., 1967) , American Mathematical Society, Providence, 1974, pp. 33–101.Google Scholar
Gambino, N., Sheaf interpretations for generalised predicative intuitionistic systems , Ph.D. thesis, University of Manchester, 2002.Google Scholar
Gambino, N., Heyting-valued interpretations for constructive set theory . Annals of Pure and Applied Logic , vol. 137 (2006), nos. 1–3, pp. 164–188.Google Scholar
Gibbons, B. J., The Veblen hierarchy explained via Mahlo hierarchies in constructive set theory , Ph.D. thesis, University of Leeds, 2002.Google Scholar
Gitik, M., All uncountable cardinals can be singular . Israel Journal of Mathematics , vol. 35 (1980), no. 1, pp. 61–88.Google Scholar
Gitman, V., Hamkins, J. D., and Johnstone, T. A., What is the theory $\mathsf{ZFC}$ without power set? Mathematical Logic Quarterly, vol. 62 (2016), nos. 4–5, pp. 391–406.Google Scholar
Gitman, V. and Schindler, R., Virtual large cardinals . Annals of Pure and Applied Logic , vol. 169 (2018), no. 12, pp. 1317–1334.Google Scholar
Gitman, V. and Schlicht, P., Between Ramsey and measurable cardinals, 2023.Google Scholar
Goldberg, G., Even ordinals and the Kunen inconsistency, 2021.Google Scholar
Grayson, R. J., Heyting-valued models for intuitionistic set theory , Applications of Sheaves , Springer, Berlin, 1979, pp. 402–414.Google Scholar
Hamkins, J. D., The wholeness axioms and V=HOD . Archive for Mathematical Logic , vol. 40 (2001), no. 1, pp. 1–8.Google Scholar
Hayut, Y. and Karagila, A., Critical cardinals . Israel Journal of Mathematics , vol. 236 (2020), no. 1, pp. 449–472.Google Scholar
Holy, P. and Lücke, P., Small models, large cardinals, and induced ideals . Annals of Pure and Applied Logic , vol. 172 (2021), no. 2, Article no. 102889, 50 pp.Google Scholar
Jeon, H., How strong is a Reinhardt set over extensions of CZF? preprint, 2021, arXiv:2101.07455.Google Scholar
Jeon, H., Constructive Ackermann’s interpretation . Annals of Pure and Applied Logic , vol. 173 (2022), no. 5, p. 103086.Google Scholar
Kanamori, A., The Higher Infinite , Springer, Berlin, 2008.Google Scholar
Kunen, K., Elementary embeddings and infinitary combinatorics . The Journal of Symbolic Logic , vol. 36 (1971), no. 3, pp. 407–413.Google Scholar
Lubarsky, R. S., Intuitionistic L , Logical Methods (Ithaca, NY, 1992) , Progr. Comput. Sci. Appl. Logic, vol. 12, Birkhäuser Boston, Boston, MA, 1993, pp. 555–571.Google Scholar
Lubarsky, R. S., IKP and friends . The Journal of Symbolic Logic , vol. 67 (2002), no. 4, pp. 1295–1322.Google Scholar
Lubarsky, R. S., CZF and second order arithmetic . Annals of Pure and Applied Logic , vol. 141 (2006), pp. 29–34.Google Scholar
Matthews, R., Large cardinals in weakened axiomatic theories , Ph.D. thesis, University of Leeds, 2021.Google Scholar
Matthews, R., Taking Reinhardt’s power away . The Journal of Symbolic Logic , vol. 87 (2022), no. 4, pp. 1643–1662.Google Scholar
Matthews, R. and Rathjen, M., Constructing the constructible universe constructively . Annals of Pure and Applied Logic , vol. 175 (2024), p. 103392.Google Scholar
McCarty, D. C., Realizability and recursive mathematics , Ph.D. thesis, Oxford University, 1984.Google Scholar
Myhill, J., Constructive set theory . The Journal of Symbolic Logic , vol. 40 (1975), no. 3, pp. 347–382.Google Scholar
Negri, S., Geometric rules in infinitary logic , Arnon Avron on Semantics and Proof Theory of Non-Classical Logics , Springer, Cham, 2021, pp. 265–293.Google Scholar
Negri, S. and Von Plato, J., Structural Proof Theory , Cambridge University Press, Cambridge, 2008.Google Scholar
Rathjen, M., The strength of some martin-löf type theories, preprint, Department of Mathematics, Ohio State University, 1993.Google Scholar
Rathjen, M., The higher infinite in proof theory . Logic Colloquium , vol. 95, 1998, pp. 275–304.Google Scholar
Rathjen, M., The realm of ordinal analysis , Sets and Proofs, Invited Papers from Logic Colloquium ’97 , London Mathematical Society Lecture Note Series, vol. 258, Cambridge University Press, New York, 1999, pp. 219–280.Google Scholar
Rathjen, M., The anti-foundation axiom in constructive set theories , Games, Logic, and Constructive Sets , CSLI Publications, Stanford, 2003, pp. 87–108.Google Scholar
Rathjen, M., Constructive set theory and Brouwerian principles . Journal of Universal Computer Science , vol. 11 (2005), no. 12, pp. 2008–2033.Google Scholar
Rathjen, M., Realizability for constructive Zermelo–Fraenkel set theory, Logic Colloquium ’03 (La Jolla, CA), Lecture Notes in Logic, vol. 24, Association for Symbolic Logic, La Jolla, 2006, pp. 282–314.Google Scholar
Rathjen, M., Constructive Zermelo–Fraenkel set theory, power set, and the calculus of constructions , Epistemology versus Ontology , Springer, Dordrecht, 2012, pp. 313–349.Google Scholar
Rathjen, M., From the weak to the strong existence property . Annals of Pure and Applied Logic , vol. 163 (2012), no. 10, pp. 1400–1418.Google Scholar
Rathjen, M., Constructive Zermelo–Fraenkel set theory and the limited principle of omniscience . Annals of Pure and Applied Logic , vol. 165 (2014), no. 2, pp. 563–572.Google Scholar
Rathjen, M., Proof theory of constructive systems: Inductive types and univalence , Feferman on Foundations , Springer, Cham, 2017, pp. 385–419.Google Scholar
Rathjen, M., Griffor, E. R., and Palmgren, E., Inaccessibility in constructive set theory and type theory . Annals of Pure and Applied Logic , vol. 94 (1998), nos. 1–3, pp. 181–200.Google Scholar
Rathjen, M. and Lubarsky, R. S., On the regular extension axiom and its variants . Mathematical Logic Quarterly , vol. 49 (2003), no. 5, pp. 511–518.Google Scholar
Reinhardt, W. N., Topics in the metamathematics of set theory, Ph.D. thesis, University of California, Berkeley, 1967.Google Scholar
Schlutzenberg, F., Extenders under ZF and constructibility of rank-to-rank embeddings, 2020.Google Scholar
Scott, D., Measurable cardinals and constructible sets . Bulletin de l’Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques , vol. 9 (1961), pp. 521–524.Google Scholar
Solovay, R. M., Reinhardt, W. N., and Kanamori, A., Strong axioms of infinity and elementary embeddings . Annals of Mathematical Logic , vol. 13 (1978), no. 1, pp. 73–116.Google Scholar
Suzuki, A., No elementary embedding from $V$ into $V$ is definable from parameters. The Journal of Symbolic Logic, vol. 64 (1999), 1591–1594.Google Scholar
Swan, A. W., CZF does not have the existence property . Annals of Pure and Applied Logic , vol. 165 (2014), no. 5, pp. 1115–1147.Google Scholar
user7247, Reducing $\mathsf{AC}$ proof to first order $\mathsf{PA}$ . MathOverflow (accessed 9 February 2022).Google Scholar
Williams, K. J., The structure of models of second-order set theories, Ph.D. thesis, The Graduate Center, The City University of New York, 2018.Google Scholar
Woodin, W. H., Suitable extender models I . Journal of Mathematical Logic , vol. 10 (2010), nos. 1–2, pp. 101–339.Google Scholar
Zapletal, J., A new proof of Kunen’s inconsistency . Proceedings of the American Mathematical Society , vol. 124 (1996), no. 7, pp. 2203–2204.Google Scholar
Ziegler, A., Large sets in constructive set theory , Ph.D. thesis, University of Leeds, 2014.Google Scholar