Published online by Cambridge University Press: 10 October 2016
We study algorithmic randomness notions via effective versions of almost-everywhere theorems from analysis and ergodic theory. The effectivization is in terms of objects described by a computably enumerable set, such as lower semicomputable functions. The corresponding randomness notions are slightly stronger than Martin–Löf (ML) randomness.
We establish several equivalences. Given a ML-random real z, the additional randomness strengths needed for the following are equivalent.
(1) all effectively closed classes containing z have density 1 at z.
(2) all nondecreasing functions with uniformly left-c.e. increments are differentiable at z.
(3) z is a Lebesgue point of each lower semicomputable integrable function.
We also consider convergence of left-c.e. martingales, and convergence in the sense of Birkhoff’s pointwise ergodic theorem. Lastly, we study randomness notions related to density of 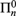 ${\rm{\Pi }}_n^0$ and
${\rm{\Pi }}_n^0$ and 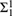 ${\rm{\Sigma }}_1^1$ classes at a real.
${\rm{\Sigma }}_1^1$ classes at a real.