Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T06:40:04.036Z Has data issue: false hasContentIssue false
  • English
  • Français

SEALING OF THE UNIVERSALLY BAIRE SETS

Part of: Set theory

Published online by Cambridge University Press:  02 July 2021

GRIGOR SARGSYAN  and
NAM TRANG
GRIGOR SARGSYAN
Affiliation:
DEPARTMENT OF MATHEMATICS RUTGERS UNIVERSITYNEW BRUNSWICK, NJ, USAE-mail: [email protected]
NAM TRANG
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NORTH TEXASDENTON, TX, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of reals is universally Baire if all of its continuous preimages in topological spaces have the Baire property. ${\sf Sealing}$ is a type of generic absoluteness condition introduced by Woodin that asserts in strong terms that the theory of the universally Baire sets cannot be changed by set forcings. The ${\sf Largest\ Suslin\ Axiom}$ ( ${\sf LSA}$ ) is a determinacy axiom isolated by Woodin. It asserts that the largest Suslin cardinal is inaccessible for ordinal definable surjections. Let ${\sf LSA}$ - ${\sf over}$ - ${\sf uB}$ be the statement that in all (set) generic extensions there is a model of $\sf {LSA}$ whose Suslin, co-Suslin sets are the universally Baire sets. 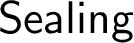We outline the proof that over some mild large cardinal theory, $\sf {Sealing}$ is equiconsistent with $\sf {LSA}$ - $\sf {over}$ - $\sf {uB}$ . In fact, we isolate an exact theory (in the hierarchy of strategy mice) that is equiconsistent with both (see Definition 3.1). 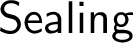As a consequence, we obtain that $\sf {Sealing}$ is weaker than the theory “ $\sf {ZFC}$ + there is a Woodin cardinal which is a limit of Woodin cardinals.” This significantly improves upon the earlier consistency proof of 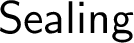$\sf {Sealing}$ by Woodin. A variation of $\sf {Sealing}$ , called 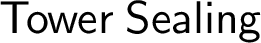$\sf {Tower \ Sealing}$ , is also shown to be equiconsistent with $\sf {Sealing}$ over the same large cardinal theory. We also outline the proof that if V has a proper class of Woodin cardinals, a strong cardinal, and a generically universally Baire iteration strategy, then $\sf {Sealing}$ holds after collapsing the successor of the least strong cardinal to be countable. 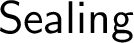This result is complementary to the aforementioned equiconsistency result, where it is shown that $\sf {Sealing}$ holds in a generic extension of a certain minimal universe. This theorem is more general in that no minimal assumption is needed. A corollary of this is that $\sf {LSA}$ - $\sf {over}$ - $\sf {uB}$ is not equivalent to $\sf {Sealing}$ .

Keywords

mouseinner model theorydescriptive set theoryhod mouse

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 03E45: Inner models, including constructibility, ordinal definability, and core models 03E60: Determinacy principles
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 27 , Issue 3 , September 2021 , pp. 254 - 266
Check for updates
Copyright
© 2021, Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Feng, Q., Magidor, M., and Woodin, H., Universally Baire sets of reals , Set Theory of the Continuum (Berkeley, CA, 1989) (H. Judah, W. Just, and H. Woodin, editors), Mathematical Sciences Research Institute Publications, vol. 26, Springer, New York, 1992, pp. 203–242.CrossRefGoogle Scholar
Kechris, A. S., Löwe, B., and Steel, J. R. (eds.), Games, Scales, and Suslin Cardinals: The Cabal Seminar, vol. I , Lecture Notes in Logic, vol. 31, Association for Symbolic Logic and Cambridge University Press, Chicago and Cambridge, 2008.CrossRefGoogle Scholar
Kechris, A. S., Löwe, B., and Steel, J. R. (eds.), Wadge Degrees and Projective Ordinals. The Cabal Seminar, vol. II , Lecture Notes in Logic, 37, Cambridge University Press, Cambridge, 2012.Google Scholar
Kechris, A. S., Löwe, B., and Steel, J. R. (eds.), Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. III , Lecture Notes in Logic, vol. 43, Cambridge University Press, Cambridge, 2016. Including reprinted papers from the Caltech-UCLA Cabal seminars held in Los Angeles, CA.CrossRefGoogle Scholar
Kechris, A. S., Martin, D. A., and Moschovakis, Y. N. (eds.), Cabal Seminar 77–79 , Lecture Notes in Mathematics, vol. 839, Springer, Berlin, 1981.CrossRefGoogle Scholar
Kechris, A. S., Martin, D. A., and Moschovakis, Y. N. (eds.), Cabal Seminar 79–81 , Lecture Notes in Mathematics, vol. 1019, Springer, Berlin, 1983.CrossRefGoogle Scholar
Kechris, A. S., Martin, D. A., and Steel, J. R. (eds.), Cabal Seminar 81–85 , Lecture Notes in Mathematics, vol. 1333, Springer, Berlin, 1988.CrossRefGoogle Scholar
Kechris, A. S. and Moschovakis, Y. N. (eds.), Cabal Seminar 76–77 , Lecture Notes in Mathematics, vol. 689, Springer, Berlin, 1978.CrossRefGoogle Scholar
Larson, P. B., The Stationary Tower , University Lecture Series, vol. 32, American Mathematical Society, Providence, 2004. Notes on a course by W. Hugh Woodin.Google Scholar
Martin, D. A. and Steel, J. R., Iteration trees . Journal of the American Mathematical Society , vol. 7 (1994), no. 1, pp. 1–73.Google Scholar
Neeman, I., Inner models in the region of a Woodin limit of Woodin cardinals . Annals of Pure and Applied Logic , vol. 116 (2002), nos. 1–3, pp. 67–155.CrossRefGoogle Scholar
Sargsyan, G., Descriptive inner model theory, this Journal, vol. 19 (2013), no. 1, pp. 1–55.Google Scholar
Sargsyan, G., Hod Mice and the Mouse Set Conjecture , Memoirs of the American Mathematical Society, vol. 236(1111), American Mathematical Society, Providence, 2015.Google Scholar
Sargsyan, G., Generic generators, to appear.Google Scholar
Sargsyan, G., Announcement of recent results in descriptive inner model theory. Available at http://www.grigorsargis.net.Google Scholar
Sargsyan, G. and Trang, N., Sealing from iterability, Transactions of the American Mathematical Society , 2019, to appear. Available at math.unt.edu/~ntrang.Google Scholar
Sargsyan, G. and Trang, N., A core model induction past the Largest Suslin Axiom, in preparation.Google Scholar
Sargsyan, G. and Trang, N., The exact consistency strength of generic absoluteness for universally Baire sets, in preparation.Google Scholar
Sargsyan, G. and Trang, N., The largest Suslin axiom, submitted. Available at math.rutgers.edu/~gs481/lsa.pdf.Google Scholar
Steel, J. R., Core models with more Woodin cardinals , The Journal of Symbolic Logic , vol. 67 (2002), no. 3, pp. 1197–1226.CrossRefGoogle Scholar
Steel, J. R., Local  ${\mathrm{K}}^{\mathrm{c}}$  constructions , The Journal of Symbolic Logic , vol. 72 (2007), no. 3, pp. 721–737.CrossRefGoogle Scholar
Steel, J. R., The derived model theorem , Logic Colloquium 2006 (S. B. Cooper, H. Geuvers, A. Pillay, and J. Vänäänen, editors), Lecture Notes in Logic, vol. 32, Association of Symbolic Logic, Chicago, 2009, pp. 280–327.CrossRefGoogle Scholar
Steel, J. R., An outline of inner model theory , Handbook of Set Theory (M. Forman and A. Kanamori, editors), Springer, Dordrecht, 2010, pp. 1595–1684.CrossRefGoogle Scholar
Steel, J. R., Normalizing iteration trees and comparing iteration strategies. Available at math.berkeley.edu/~steel/papers/Publications.html.Google Scholar
Hugh Woodin, W., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal , revised ed., De Gruyter Series in Logic and Its Applications, vol. 1, Walter de Gruyter GmbH, Berlin, 2010.CrossRefGoogle Scholar
Hugh Woodin, W., In search of ultimate-L: The 19 th Midrasha mathematicae lectures, this Journal, vol. 23 (2017), no. 1, pp. 1–109.Google Scholar