Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-21T18:01:08.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Reverse Mathematics and Π12 Comprehension

Published online by Cambridge University Press:  15 January 2014

Carl Mummert  and
Stephen G. Simpson
Carl Mummert
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, State College, PA, 16802, USA, E-mail: [email protected], URL: http://www.math.psu.edu/mummert/, E-mail: [email protected], URL: http://www.math.psu.edu/simpson/
Stephen G. Simpson
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, State College, PA, 16802, USA, E-mail: [email protected], URL: http://www.math.psu.edu/mummert/, E-mail: [email protected], URL: http://www.math.psu.edu/simpson/
Get access Rights & Permissions [Opens in a new window]

Abstract

We initiate the reverse mathematics of general topology. We show that a certain metrization theorem is equivalent to Π12 comprehension. An MF space is defined to be a topological space of the form MF(P) with the topology generated by {Np ∣ p ϵ P}. Here P is a poset, MF(P) is the set of maximal filters on P, and Np = {F ϵ MF(P) ∣ p ϵ F }. If the poset P is countable, the space MF(P) is said to be countably based. The class of countably based MF spaces can be defined and discussed within the subsystem ACA0 of second order arithmetic. One can prove within ACA0 that every complete separable metric space is homeomorphic to a countably based MF space which is regular. We show that the converse statement, “every countably based MF space which is regular is homeomorphic to a complete separable metric space,” is equivalent to . 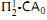The equivalence is proved in the weaker system 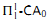. This is the first example of a theorem of core mathematics which is provable in second order arithmetic and implies Π12 comprehension.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 11 , Issue 4 , December 2005 , pp. 526 - 533
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Harrington, Leo A., Kechris, Alexander S., and Louveau, Alain, A Glimm-Effros dichotomy for Borel equivalence relations, Journal of the American Mathematical Society, vol. 3 (1990), pp. 903-928.CrossRefGoogle Scholar
[2] Heinatsch, Christoph and Möllerfeld, Michael, The determinacy strength of Π1 2 comprehension, Preprint, 11 pages, 02 10, 2005, submitted for publication.Google Scholar
[3] Kechris, Alexander S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, Springer, 1985.Google Scholar
[4] Kechris, Alexander S. and Louveau, Alain, The classification of hypersmooth Borel equivalence relations, Journal of the American Mathematical Society, vol. 10 (1997), pp. 215-242.Google Scholar
[5] Kelley, John L., General Topology, Van Nostrand, 1955.Google Scholar
[6] Ko, K., Nerode, A., Pour-El, M. B., Weihrauch, K., and Wiedermann, J. (editors), Computability and complexity in analysis, Informatik-Berichte, vol. 235, Fernuniversität Hagen, 08 1998.Google Scholar
[7] Kunen, Kenneth, Set Theory, an Introduction to Independence Proofs, Studies in Logic and the Foundations of Mathematics, North-Holland, 1980.Google Scholar
[8] Mummert, Carl, On the Reverse Mathematics of General Topology, Ph.D. thesis, The Pennsylvania State University, 2005.Google Scholar
[9] Mummert, Carl, Reverse mathematics of MF spaces, In preparation, 2005.Google Scholar
[10] Schröder, Matthias, Effective metrization of regular spaces, In Ko et al. [6], pp. 63-80.Google Scholar
[11] Simpson, Stephen G., Subsystems of Second Order Arithmetic, Perspectives in Mathematical Logic, Springer, 1999.Google Scholar
[12] Simpson, Stephen G. (editor), Reverse Mathematics 2001, Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, 2005.Google Scholar