Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Adams, Scot
and
Kechris, Alexander
2000.
Linear algebraic groups and countable Borel equivalence relations.
Journal of the American Mathematical Society,
Vol. 13,
Issue. 4,
p.
909.
Clemens, John D.
Gao, Su
and
Kechris, Alexander S.
2001.
Polish Metric Spaces: Their Classification and Isometry Groups.
Bulletin of Symbolic Logic,
Vol. 7,
Issue. 3,
p.
361.
JACKSON, S.
KECHRIS, A. S.
and
LOUVEAU, A.
2002.
COUNTABLE BOREL EQUIVALENCE RELATIONS.
Journal of Mathematical Logic,
Vol. 02,
Issue. 01,
p.
1.
Hirschfeldt, Denis R.
Khoussainov, Bakhadyr
Shore, Richard A.
and
Slinko, Arkadii M.
2002.
Degree spectra and computable dimensions in algebraic structures.
Annals of Pure and Applied Logic,
Vol. 115,
Issue. 1-3,
p.
71.
Кановей, Владимир Григорьевич
Kanovei, Vladimir Grigor'evich
Реекен, М
and
Reeken, M
2003.
Некоторые новые результаты о борелевской несводимости отношений эквивалентности.
Известия Российской академии наук. Серия математическая,
Vol. 67,
Issue. 1,
p.
59.
Tsirelson, Boris
2004.
Nonclassical stochastic flows and continuous products.
Probability Surveys,
Vol. 1,
Issue. none,
Kanovei, V. G.
and
Lyubetsky, V. A.
2006.
A confinal family of equivalence relations and Borel ideals generating them.
Proceedings of the Steklov Institute of Mathematics,
Vol. 252,
Issue. 1,
p.
85.
Ferenczi, Valentin
and
Galego, Elói Medina
2006.
Some equivalence relations which are borel reducible to isomorphism between separable banach spaces.
Israel Journal of Mathematics,
Vol. 152,
Issue. 1,
p.
61.
Tsirelson, Boris
2006.
Brownian local minima, random dense countable sets and random equivalence classes.
Electronic Journal of Probability,
Vol. 11,
Issue. none,
Kanovei, V. G.
Lyubetskii, V. A.
and
Reeken, M.
2007.
Reducibility of monadic equivalence relations.
Mathematical Notes,
Vol. 81,
Issue. 5-6,
p.
757.
Кановей, Владимир Григорьевич
Kanovei, Vladimir Grigor'evich
Любецкий, Василий Александрович
Lyubetskii, Vasilii Aleksandrovich
Реекен, М
and
Reeken, M
2007.
О сводимости монадических отношений эквивалентности.
Математические заметки,
Vol. 81,
Issue. 6,
p.
842.
Friedman, Sy-David
and
Kanovei, Vladimir
2008.
Some natural equivalence relations in the Solovay model.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 78,
Issue. 1,
p.
91.
Fokina, Ekaterina B.
and
Friedman, Sy-David
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
198.
Fokina, Ekaterina B.
Friedman, Sy-David
and
Törnquist, Asger
2010.
The effective theory of Borel equivalence relations.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
837.
Kanovei, Vladimir
2010.
A weak dichotomy below E1×E3.
Topology and its Applications,
Vol. 157,
Issue. 8,
p.
1465.
Hjorth, Greg
2010.
Handbook of Set Theory.
p.
297.
Fokina, Ekaterina B.
Friedman, Sy-David
Harizanov, Valentina
Knight, Julia F.
Mccoy, Charles
and
Montalbán, Antonio
2012.
Isomorphism relations on computable structures.
The Journal of Symbolic Logic,
Vol. 77,
Issue. 1,
p.
122.
Fokina, Ekaterina B.
and
Friedman, Sy‐David
2012.
On Σ11 equivalence relations over the natural numbers.
Mathematical Logic Quarterly,
Vol. 58,
Issue. 1-2,
p.
113.
Doberkat, Ernst-Erich
2012.
Lattice properties of congruences for stochastic relations.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 8,
p.
1016.
FOUCHÉ, WILLEM L.
2015.
Kolmogorov complexity and the geometry of Brownian motion.
Mathematical Structures in Computer Science,
Vol. 25,
Issue. 7,
p.
1590.
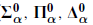 sets). After this come the projective sets, obtained by starting with the Borel sets and closing under the operations of complementation and projection, and the corresponding projective hierarchy (
sets). After this come the projective sets, obtained by starting with the Borel sets and closing under the operations of complementation and projection, and the corresponding projective hierarchy (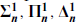 sets).
sets).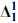 ), analytic (
), analytic (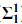 ) and coanalytic (
) and coanalytic ( ) sets.
) sets.