Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T13:22:31.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Mass Problems and Randomness

Published online by Cambridge University Press:  15 January 2014

Stephen G. Simpson
Stephen G. Simpson*
Affiliation:
Department of Mathematics, Pennsylvania State University, State College, PA 16802, USAE-mail: [email protected], URL: http://www.math.psu.edu/simpson/
Get access Rights & Permissions [Opens in a new window]

Abstract

A mass problem is a set of Turing oracles. If P and Q are mass problems, we say that P is weakly reducible to Q if every member of Q Turing computes a member of P. We say that P is strongly reducible to Q if every member of Q Turing computes a member of P via a fixed Turing functional. The weak degrees and strong degrees are the equivalence classes of mass problems under weak and strong reducibility, respectively. 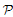We focus on the countable distributive lattices ω and 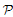s of weak and strong degrees of mass problems given by nonempty subsets of 2ω. Using an abstract Gödel/Rosser incompleteness property, we characterize the subsets of 2ω whose associated mass problems are of top degree in 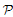ω and 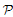s, respectively Let R be the set of Turing oracles which are random in the sense of Martin-Löf, and let r be the weak degree of R. We show that r is a natural intermediate degree within 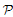ω. Namely, we characterize r as the unique largest weak degree of a subset of 2ω of positive measure. Within 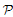ω we show that r is meet irreducible, does not join to 1, and is incomparable with all weak degrees of nonempty thin perfect subsets of 2ω. In addition, we present other natural examples of intermediate degrees in 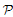ω. We relate these examples to reverse mathematics, computational complexity, and Gentzen-style proof theory.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 11 , Issue 1 , March 2005 , pp. 1 - 27
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ambos-Spies, K., Müller, G. H., and Sacks, G. E. (editors), Recursion theory week, Lecture Notes in Mathematics, no. 1432, Springer-Verlag, 1990.Google Scholar
[2] Ambos-Spies, Klaus, Kjos-Hanssen, Björn, Lempp, Steffen, and SlaMan, Theodore A., Comparing DNR and WWKL, The Journal of Symbolic Logic, vol. 69 (2004), pp. 1089–1104.Google Scholar
[3] Binns, Stephen, The Medvedev and Muchnik lattices of classes, Ph.D. thesis , Pennsylvania State University, 08 2003.Google Scholar
[4] Binns, Stephen, A splitting theorem for the Medvedev and Muchnik lattices, Mathematical Logic Quarterly, vol. 49 (2003), pp. 327–335.Google Scholar
[5] Binns, Stephen, Small classes, Archive for Mathematical Logic, (2004), preprint, 10 2003, 22 pages, accepted for publication.Google Scholar
[6] Binns, Stephen and Simpson, Stephen G., Embeddings into the Medvedev and Muchnik lattices of classes, Archive for Mathematical Logic, vol. 43 (2004), pp. 399–414.Google Scholar
[7] Brown, Douglas K., Giusto, Mariagnese, and Simpson, Stephen G., Vitali's theorem and WWKL, Archive for Mathematical Logic, vol. 41 (2002), pp. 191–206.Google Scholar
[8] Bruscoli, P. and Guglielmi, A. (editors), Summer school and workshop on proof theory, computation and complexity, Dresden, 2003, Electronic Notes in Theoretical Computer Science, Elsevier, 2004, to appear.Google Scholar
[9] Cenzer, Douglas and Hinman, Peter G., Density of the Medvedev lattice of classes, Archive for Mathematical Logic, vol. 42 (2003), pp. 583–600.Google Scholar
[10] Cenzer, Douglas and Remmel, Jeffrey B., classes in mathematics, In Ershov, et al. [20], Volumes 1 and 2, pp. 623–821.Google Scholar
[11] Cholak, Peter, Coles, Richard, Downey, Rod, and Herrmann, Eberhard, Automorphisms of the lattice of classes; perfect thin classes and ANC degrees, Transactions of the American Mathematical Society, vol. 353 (2001), pp. 4899–4924.CrossRefGoogle Scholar
[12] COMP-THY e-mail list, http://listserv.nd.edu/archives/comp-thy.html, 09 1995 to the present.Google Scholar
[13] Cooper, S. B., Slaman, T. A., and Wainer, S. S. (editors), Computability, enumerability, unsolvability: Directions in recursion theory, London Mathematical Society Lecture Notes, no. 224, Cambridge University Press, 1996.CrossRefGoogle Scholar
[14] Demuth, Oswald, A notion of semigenericity, Commentationes Mathematicae Universitatis Carolinae, vol. 28 (1987), pp. 71–84.Google Scholar
[15] Downey, Rodney G., Jockusch, Carl G. Jr., and Stob, Michael, Array nonrecursive sets andmultiplepermitting arguments, In Ambos-Spies, et al. [1], pp. 141–174.Google Scholar
[16] Downey, Rodney G., Jockusch, Carl G. Jr., and Stob, Michael, Array nonrecursive degrees and genericity, In Cooper, et al. [13], pp. 93–105.CrossRefGoogle Scholar
[17] Drake, F. R. and Truss, J. K. (editors), Logic colloquium '86, Studies in Logic and the Foundations of Mathematics, North-Holland, 1988.Google Scholar
[18] Ebbinghaus, H.-D., Fernandez-Prida, J., Garrido, M., Lascar, D., and Artalejo, M. Rodriguez (editors), Logic colloquium '87, Studies in Logic and the Foundations of Mathematics, North-Holland, 1989.Google Scholar
[19] Ebbinghaus, H.-D., Müller, G. H., and Sacks, G. E. (editors), Recursion theory week, Lecture Notes in Mathematics, no. 1141, Springer-Verlag, 1985.CrossRefGoogle Scholar
[20] Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B. (editors), Handbook ofrecursive mathematics, Studies in Logic and the Foundations of Mathematics, North-Holland, 1998, Volumes 1 and 2.Google Scholar
[21] Fenstad, J.-E., Frolov, I. T., and Hilpinen, R. (editors), Logic, methodology and philosophy ofscience VIII. Proceedings of the 8th international conference on logic, methodology and philosophy of science, Moscow, 1987, Studies in Logic and the Foundations of Mathematics, North-Holland, 1989.Google Scholar
[22] FOM e-mail list, http://www.cs.nyu.edu/mailman/listinfo/fom/, 09 1997 to the present.Google Scholar
[23] Giusto, Mariagnese and Simpson, Stephen G., Located sets and reverse mathematics, The Journal of Symbolic Logic, vol. 65 (2000), pp. 1451–1480.Google Scholar
[24] Gruska, J., Rovan, B., and Wiedermann, J. (editors), Mathematical foundations of computer science, Lecture Notes in Computer Science, no. 233, Springer-Verlag, 1986.Google Scholar
[25] Jockusch, Carl G. Jr., Degrees offunctions with no fixed points, In Fenstad et al. [21], pp. 191–201.Google Scholar
[26] Jockusch, Carl G. Jr. and Soare, Robert I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 35–56.Google Scholar
[27] Kautz, Steven M., Degrees of random sets, Ph.D. thesis , Cornell University, 1991.Google Scholar
[28] Kurtz, Stuart A., Randomness and genericity in the degrees of unsolvability, Ph.D. thesis , University of Illinois at Urbana-Champaign, 1981.Google Scholar
[29] Kučera, Antonín, Measure, classes and complete extensions of PA, In Ebbinghaus et al. [19], pp. 245–259.Google Scholar
[30] Kučera, Antonín, An alternative, priority-free, solution to Post's problem, In Gruska et al. [24], pp. 493–500.Google Scholar
[31] Kučera, Antonín, On the role of 0′ in recursion theory, In Drake and Truss [17], pp. 133–141.Google Scholar
[32] Kučera, Antonín, On the use of diagonally nonrecursive functions, In Ebbinghaus et al. [18], pp. 219–239.Google Scholar
[33] Kučera, Antonín, Randomness and generalizations of fixed point free functions, In Ambos-Spies et al. [1], pp. 245–254.Google Scholar
[34] Kučera, Antonín, On relative randomness, Annals of Pure and Applied Logic, vol. 63 (1993), pp. 61–67.Google Scholar
[35] Kučera, Antonín and Terwijn, Sebastiaan A., Lowness for the class of random sets, The Journal of Symbolic Logic, vol. 64 (1999), pp. 1396–1402.Google Scholar
[36] Lerman, Manuel, Degrees of unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, 1983.CrossRefGoogle Scholar
[37] Li, Ming and Vitányi, Paul, An introduction to Kolmogorov complexity and its applications, 2nd ed., Graduate Texts in Computer Science, Springer-Verlag, 1997.Google Scholar
[38] Martin, Donald A. and Pour-El, Marian B., Axiomatizable theories with few ax-iomatizable extensions, The Journal of Symbolic Logic, vol. 35 (1970), pp. 205–209.Google Scholar
[39] Martin-Löf, Per, The definition of random sequences, Information and Control, vol. 9 (1966), pp. 602–619.Google Scholar
[40] Medvedev, Yuri T., Degrees of difficulty of mass problems, Doklady Akademii Nauk SSSR, N.S., vol. 104 (1955), pp. 501–504, In Russian.Google Scholar
[41] Muchnik, A. A., On strong and weak reducibilities of algorithmic problems, Sibirskii Matematicheskii Zhurnal, vol. 4 (1963), pp. 1328–1341, In Russian.Google Scholar
[42] Odifreddi, Piergiorgio, Classical recursion theory, Studies in Logic and the Foundations of Mathematics, no. 125, North-Holland, 1989.Google Scholar
[43] Odifreddi, Piergiorgio, Classical recursion theory, volume 2, Studies in Logic and the Foundations of Mathematics, no. 143, North-Holland, 1999.Google Scholar
[44] Post, Emil L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.Google Scholar
[45] Rogers, Hartley Jr., Theory of recursive functions and effective computability, McGraw-Hill, 1967.Google Scholar
[46] Sacks, Gerald E., Degrees of unsolvability, Annals of Mathematics Studies, no. 55, Princeton University Press, 1963.Google Scholar
[47] Simpson, Stephen G., FOM: natural r.e. degrees; Pi01 classes, FOM e-mail list [22], 08 13, 1999.Google Scholar
[48] Simpson, Stephen G., FOM: priority arguments; Kleene-r.e. degrees; Pi01 classes, FOM e-mail list [22], 08 16, 1999.Google Scholar
[49] Simpson, Stephen G., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, 1999.Google Scholar
[50] Simpson, Stephen G., Medvedev degrees of nonempty Pi^0_1 subsets of 2 ^ omega, COMP-THY e-mail list [12], 06 9, 2000.Google Scholar
[51] Simpson, Stephen G., sets and models of WKL0, [54], preprint, 04 2000, 29 pages, to appear.Google Scholar
[52] Simpson, Stephen G., Mass problems,In Bruscoli and Guglielmi [8], preprint, 05 24, 2004, 24 pages, to appear.Google Scholar
[53] Simpson, Stephen G., An extension of the recursively enumerable Turing degrees, preprint, 08 10, 2004, 15 pages, submitted for publication, 2004.Google Scholar
[54] Simpson, Stephen G. (editor), Reverse mathematics 2001, Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, 2004, to appear.Google Scholar
[55] Simpson, Stephen G. and Slaman, Theodore A., Medvedev degrees of , subsets of 2ω , preprint, 07 2001, 4 pages, in preparation.Google Scholar
[56] Soare, Robert I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, 1987.CrossRefGoogle Scholar
[57] Sorbi, Andrea, The Medvedev lattice of degrees of difficulty, In Cooper et al. [13], pp. 289–312.CrossRefGoogle Scholar
[58] Terwijn, Sebastiaan A., The Medvedev lattice of computably closed sets, Archive for Mathematical Logic, (2004), preprint, 06 2004, 22 pages, to appear.Google Scholar
[59] Turing, Alan M., On computable numbers, with an application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, vol. 42 (1936), pp. 230–265.Google Scholar
[60] Wainer, Stanley S., A classification of the ordinal recursive functions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 13 (1970), pp. 136–153.Google Scholar
[61] Yu, Xiaokang and Simpson, Stephen G., Measure theory and weak Königs lemma, Archive for Mathematical Logic, vol. 30 (1990), pp. 171–180.Google Scholar