Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-09T06:34:29.265Z Has data issue: false hasContentIssue false
  • English
  • Français

GOODSTEIN SEQUENCES BASED ON A PARAMETRIZED ACKERMANN–PÉTER FUNCTION

Part of: Proof theory and constructive mathematics Computability and recursion theory

Published online by Cambridge University Press:  02 July 2021

TOSHIYASU ARAI ,
STANLEY S. WAINER  and
ANDREAS WEIERMANN
TOSHIYASU ARAI
Affiliation:
UNIVERSITY OF TOKYOTOKYO, JAPANE-mail: [email protected]
STANLEY S. WAINER
Affiliation:
UNIVERSITY OF LEEDSLEEDS, UKE-mail: [email protected]
ANDREAS WEIERMANN
Affiliation:
UNIVERSITY OF GHENTGHENT, BELGIUME-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Following our [6], though with somewhat different methods here, further variants of Goodstein sequences are introduced in terms of parameterized Ackermann–Péter functions. Each of the sequences is shown to terminate, and the proof-theoretic strengths of these facts are calibrated by means of ordinal assignments, yielding independence results for a range of theories: PRA, PA, 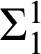$\Sigma ^1_1$ -DC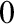 $_0$ , ATR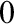 $_0$ , up to ID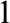 $_1$ . The key is the so-called “Hardy hierarchy” of proof-theoretic bounding finctions, providing a uniform method for associating Goodstein-type sequences with parameterized normal form representations of positive integers.

Keywords

proof-theoretic ordinalsfast-growing functionsHardy hierarchyindependence results

MSC classification

Primary: 03F15: Recursive ordinals and ordinal notations
Secondary: 03F25: Relative consistency and interpretations 03F30: First-order arithmetic and fragments 03F35: Second- and higher-order arithmetic and fragments 03D55: Hierarchies
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 27 , Issue 2 , June 2021 , pp. 168 - 186
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrusci, V. M., Girard, J.-Y., and Van de Wiele, J., Some uses of dilators in combinatorial problems, part I, Logic and Combinatorics (Simpson, S. G., editor), Contemporary Mathematics, vol. 65, American. Mathematical Society, Providence, RI, 1987, pp. 25–53.CrossRefGoogle Scholar
Aguilera, J. P., Freund, A., Rathjen, M., and Weiermann, A., Ackermann and Goodstein go functorial, preprint, 2020, math. arXiv:2011.03439, under submission.Google Scholar
Arai, T., Some results on cut-elimination, provable well-orderings, induction and reflection. Annals of Pure and Applied Logic, vol. 95 (1998), pp. 93–184.CrossRefGoogle Scholar
Arai, T., Grzegorczyk sequences, preprint, 2020, math. arXiv:1811.09958.Google Scholar
Arai, T., Ordinal Analysis with an Introduction to Proof Theory, Springer, New York, 2020.CrossRefGoogle Scholar
Arai, T., Fernández-Duque, D., Wainer, S. S., and Weiermann, A., Predicatively unprovable termination of the Ackermannian Goodstein process. Proceedings of the American Mathematical Society, vol. 148 (2020), no. 8, pp. 3567–3582.CrossRefGoogle Scholar
Buchholz, W., Cichon, E. A., and Weiermann, A., A uniform approach to fundamental sequences and hierarchies. Mathematical Logic Quarterly, vol. 40 (1994), pp. 273–286.CrossRefGoogle Scholar
Buchholz, W. and Wainer, S. S., Provably computable functions and the fast growing hierarchy, Logic and Combinatorics (Simpson, S. G., editor), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 179–198.CrossRefGoogle Scholar
Cantini, A., On the relation between choice and comprehension principles in second order arithmetic. Journal of Symbolic Logic, vol. 51 (1986), pp. 360–373.CrossRefGoogle Scholar
Cichon, E. A., A short proof of two recently discovered independence proofs using recursion theoretic methods. Proceedings of the American Mathematical Society, vol. 87 (1983), pp. 704–706.CrossRefGoogle Scholar
Cichon, E. A. and Wainer, S. S., The slow-growing and the Grzegorczyk hierarchies. Journal of Symbolic Logic, vol. 48 (1983), pp. 399–408.Google Scholar
Fairtlough, M. and Wainer, S. S., Hierarchies of provably recursive functions, Handbook of Proof Theory (Buss, S. R., editor), Studies in Logic and Foundations of Mathematics, vol. 137, Elsevier, London, 1998, pp. 149–207.CrossRefGoogle Scholar
Feferman, S., Systems of predicative analysis II. Journal of Symbolic Logic, vol. 33 (1968), pp. 193–220.Google Scholar
Goodstein, R. L., On the restricted ordinal theorem. Journal of Symbolic Logic, vol. 9 (1944), pp. 33–41.Google Scholar
Kirby, L. A. S. and Paris, J. B., Accessible independence results for Peano arithmetic. Bulletin of the London Mathematical Society, vol. 14 (1982), pp. 285–293.CrossRefGoogle Scholar
Rathjen, M., Goodstein’s theorem revisited, Gentzen’s Centenary: The Quest for Consistency (Kahle, R. and Rathjen, M., editors), Springer, London, 2015, pp. 229–242.CrossRefGoogle Scholar
Schwichtenberg, H. and Wainer, S. S., Proofs and Computations, ASL Perspectives in Logic, Cambridge University Press, Cambridge, 2012.Google Scholar
Weiermann, A., Classifying the provably total functions of PA, this Journal, vol. 12 (2006), pp. 177–190.Google Scholar
Weiermann, A., An independence result for ID ${}_1$ via Arai style Goodstein sequences, unpublished notes, 2019.Google Scholar
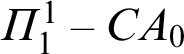Wilken, G. and Weiermann, A., Goodstein sequences for prominent ordinals up to the ordinal of ${\varPi}_1^1-{\mathsf{\mathit{CA}}}_0$ . Annals of Pure and Applied Logic, vol. 164 (2013), pp. 1493–1506.Google Scholar