Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-31T13:53:27.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry, Calculus and Zil'ber's Conjecture

Published online by Cambridge University Press:  15 January 2014

Ya'acov Peterzil  and
Sergei Starchenko
Ya'acov Peterzil
Affiliation:
Department of Mathematics and Computer Science, Haifa University, Haifa, Israel.E-mail: [email protected]
Sergei Starchenko
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN 37240, USA.E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

§1. Introduction. By and large, definitions of a differentiable structure on a set involve two ingredients, topology and algebra. However, in some cases, partial information on one or both of these is sufficient. A very simple example is that of the field ℝ (or any real closed field) where algebra alone determines the ordering and hence the topology of the field:

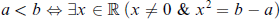
In the case of the field ℂ, the algebraic structure is insufficient to determine the Euclidean topology; another topology, Zariski, is associated with the ield but this will be too coarse to give a diferentiable structure.

A celebrated example of how partial algebraic and topological data (G a locally euclidean group) determines a differentiable structure (G is a Lie group) is Hilbert's 5th problem and its solution by Montgomery-Zippin and Gleason.

The main result which we discuss here (see [13] for the full version) is of a similar flavor: we recover an algebraic and later differentiable structure from a topological data. We begin with a linearly ordered set ⟨M, <⟩, equipped with the order topology, and its cartesian products with the product topologies. We then consider the collection of definable subsets of Mn, n = 1, 2, …, in some first order expansion ℳ of ⟨M, <⟩.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 2 , Issue 1 , March 1996 , pp. 72 - 83
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Hrushovski, E., The Mordell-Lang conjecture for function fields, preprint.Google Scholar
[2] Hrushovski, E., Contributions to stable model theory, Ph.D. thesis , Berkeley, 1986.Google Scholar
[3] Hrushovski, E., A new strongly minimal set, Annals of Pure and Applied Logic, vol. 62 (1993), pp. 147–166.Google Scholar
[4] Hrushovski, E. and Pillay, A., Weakly normal groups, Logic Colloquium, vol. 85.Google Scholar
[5] Hrushovski, E. and Pillay, A., Groups definable in local fields and pseudo-finite fields, Israel Journal of Mathematics, vol. 85 (1994), pp. 203–262.Google Scholar
[6] Hrushovski, E. and Zil'ber, B., Zariski geometries, to appear.Google Scholar
[7] Hrushovski, E. and Zil'ber, B., Zariski geometries, Bulletin (New Series) of the AMS, vol. 28 (1993), no. 2, pp. 315–323.Google Scholar
[8] Knight, J., Pillay, A., and Steinhorn, C., Definable sets in ordered structures II, Transactions of the AMS, vol. 295 (1986), pp. 593–605.Google Scholar
[9] Loveys, J. and Peterzil, Y., Linear o-minimal structures, Israel Journal of Mathematics, vol. 81 (1993), pp. 1–30.Google Scholar
[10] Marker, D., Peterzil, Y., and Pillay, A., Additive reducts of real closed fields, Journal of Symbolic Logic, vol. 57 (1992), no. 1, pp. 109–117.Google Scholar
[11] Peterzil, Y., Constructing a group-interval in o-minimal structures, Journal of Pure and Applied Algebra, vol. 94 (1994), pp. 85–100.Google Scholar
[12] Peterzil, Y., Pillay, A., and Starchenko, S., A classification of simple groups in o-minimal structures, in preparation.Google Scholar
[13] Peterzil, Y. and Starchenko, S., A trichotomy theorem for o-minimal structures, preprint.Google Scholar
[14] Pillay, A., An introduction to stability theory, Clarendon Press, Oxford, 1983.Google Scholar
[15] Pillay, A. and Steinhorn, C., Definable sets in ordered structures I, Transactions of the AMS, vol. 295 (1986), pp. 565–592.Google Scholar
[16] Rabinovich, E., Definability of a field in sufficiently rich incidence systems, Maths Notes 14, Queen Mary and Westfield College, University of London, 1986.Google Scholar
[17] van den Dries, L., Tame topology and o-minimal structures, preliminary version, 1991.Google Scholar
[18] Wilkie, A., Model completeness results for expansions of the real field II: The exponential function, to appear.Google Scholar
[19] Zil'ber, B., Structural properties of models of ℵ1-categorical theories, Logic methodology and philosophy of science VII (Marcus, R. Barcon et al., editors), North Holland, Amsterdam, 1986, pp. 115–128.Google Scholar