Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T14:11:58.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Counterexamples of the 0-1 Law for Fragments of Existential Second-Order Logic: an Overview

Published online by Cambridge University Press:  15 January 2014

Jean-Marie Le Bars
Jean-Marie Le Bars*
Affiliation:
Informatique, Greyc, Université De Caen Caen, FranceE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

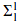We propose an original use of techniques from random graph theory to find a Monadic (Minimal Scott without equality) sentence without an asymptotic probability. Our result implies that the 0-1 law fails for the logics 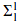(FO2) and] 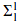(Minimal Gödel without equality). Therefore we complete the classification of first-order prefix classes with or without equality, according to the existence of the 0-1 law for the corresponding 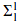fragment. In addition, our counterexample can be viewed as a single explanation of the failure of the 0-1 law of all the fragments of existential second-order logic for which the failure is already known.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 6 , Issue 1 , March 2000 , pp. 67 - 82
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bollobás, B., Graph theory, an introduction course, Springer-Verlag, 1979.Google Scholar
[2] Bollobás, B., Random graphs, Academic Press, 1985.Google Scholar
[3] Bollobás, B. and Erdös, P., Cliques in random graphs, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 80 (1976), pp. 419–427.CrossRefGoogle Scholar
[4] Chvatal, V., On the computational complexity of finding a kernel, Technical report, Report NO CRM-300, 1973, Universite de Montréal, Centre de Recherches Mathématiques.Google Scholar
[5] Creignou, N., The class of problems that are linearly equivalent to satisfiability or a uniform method for proving NP-completeness, Theoretical Computer Science, vol. 145 (1995), pp. 111–145.CrossRefGoogle Scholar
[6] Dreben, D. and Goldfarb, W. D., The decision problem: Solvable classes of quantificational formulas, Addison-Wesley, 1979.Google Scholar
[7] Erdös, P. and Rényi, A., On the evolution of random graphs, Publ. Math. Inst. Hungar. Acad. Sci., vol. 7 (1960), pp. 17–61.Google Scholar
[8] Erdös, P. and Spencer, J., Probabilistic method in combinatorics, A Series of Monographs and Textbooks, Academic Press, 1974.Google Scholar
[9] Fagin, R., Generalized first-order spectra and polynomial time recognizable sets, Complexity of computations (Karp, R., editor), SIAM-AMS Proceedings, vol. 7, American Mathematical Society, Providence, RI, 1974, pp. 43–73.Google Scholar
[10] Fagin, R., Probabilities on finite models, The Journal of Symbolic Logic, vol. 41 (1976), pp. 50–58.CrossRefGoogle Scholar
[11] De La Vega, W. Fernandez, Kernel on random graphs, Discrete Mathematics, vol. 82 (1990), pp. 213–217.CrossRefGoogle Scholar
[12] Flum, J., Problems in finite model theory collected in Oberwolfach, 1994.Google Scholar
[13] Glebskii, Y. V., Kogan, D.I., Liogonki, M. I., and Talanov, V. A., Range and degree of realizability of formulas in the restricted predicate calculus, Cybernetics, vol. 5 (1969), pp. 142–154.CrossRefGoogle Scholar
[14] Goldfarb, W. D., The Gödel class with identity is unsolvable, Bulletin of the American Mathematical Society, vol. 10(1) (01 1984), pp. 113–115.CrossRefGoogle Scholar
[15] Kaufmann, M., Counterexample to the 0-1 law for existential monadic second-order logic, Technical report, CLI Internal Note 32, Computational Logic Inc., 12 1987, paper available at ftp://ftp.informatik.rwth-aachen.de/pub/FMT/jurek/kaufmann.ps.Google Scholar
[16] Kaufmann, M. and Shelah, S., On random models of finite power and monadic logic, Discrete mathematics, vol. 54 (1985), pp. 285–293.CrossRefGoogle Scholar
[17] Kolaitis, PH. G. and Vardi, M. Y., The decision problem for the probabilities of higherorder properties, Proceedings of the 19th ACM Symposium on Theory of Computing, STOC'87, 1987, pp. 425–435.Google Scholar
[18] Kolaitis, PH. G. and Vardi, M. Y., 0-1 laws and decisions problems for fragments of second-order logic, Information and Computation, vol. 87 (1990), pp. 302–338.CrossRefGoogle Scholar
[19] Kolaitis, PH. G. and Vardi, M. Y., 0-1 laws for fragments of second-order logic: an overview, Logic from computer science (Proceedings of Workshop, 1989) (Moschovakis, Y.N., editor), 1992, pp. 265–286.CrossRefGoogle Scholar
[20] Bars, J-M. Le, Fragments of existential second-order logic without 0-1 laws, Proceedings of the 13th IEEE Symposium on Logic in Computer Science, 1998.Google Scholar
[21] Bars, J-M. Le, Probabilités asymptotiques et pouvoir d'expression des fragments de la logique du second ordre, Ph.D. thesis , University of Caen, 1998.Google Scholar
[22] Mortimer, M., On languages with two variables, Zeischrift für Mathematische Logik und Grundlagen der Mathematik, vol. 21 (1975), pp. 135–140.CrossRefGoogle Scholar
[23] Pacholski, L. and Szwast, W., Asymptotic probabilities of existential second-order Gödel sentences, The Journal of symbolic logic, vol. 56 (1991), pp. 427–438.CrossRefGoogle Scholar
[24] Pacholski, L. and Szwast, W., A counterexample to the 0-1 law for the class of existential second-order minimal Gödel sentences with equality, Information and Computation, vol. 107 (1993), pp. 91–103.CrossRefGoogle Scholar
[25] Palmer, E. M., Graphical evolution: An introduction to the theory of random graphs, Wiley, 1985.Google Scholar
[26] Tendera, L., A note on asymptotic probabilities of existential second-order minimal classes: the last step, Fundamenta Informaticae, vol. 20 (1994), pp. 277–285.CrossRefGoogle Scholar
[27] Vedø, A., Asymptotic probabilities for second-order existential Kahr-Moore-Wang sentences, The Journal of Symbolic Logic, vol. 62 (03 1997), pp. 304–319.CrossRefGoogle Scholar