Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-23T00:30:35.406Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORICAL QUANTIFICATION

Part of: Model theory Proof theory and constructive mathematics General logic Philosophical aspects of logic and foundations

Published online by Cambridge University Press:  24 January 2024

CONSTANTIN C. BRÎNCUŞ Open the ORCID record for CONSTANTIN C. BRÎNCUŞ [Opens in a new window]
CONSTANTIN C. BRÎNCUŞ*
Affiliation:
FACULTY OF PHILOSOPHY UNIVERSITY OF BUCHAREST BUCHAREST 060024, ROMANIA INSTITUTE OF PHILOSOPHY AND PSYCHOLOGY, ROMANIAN ACADEMY BUCHAREST 050731, ROMANIA E-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Due to Gödel’s incompleteness results, the categoricity of a sufficiently rich mathematical theory and the semantic completeness of its underlying logic are two mutually exclusive ideals. For first- and second-order logics we obtain one of them with the cost of losing the other. In addition, in both these logics the rules of deduction for their quantifiers are non-categorical. In this paper I examine two recent arguments—Warren [43] and Murzi and Topey [30]—for the idea that the natural deduction rules for the first-order universal quantifier are categorical, i.e., they uniquely determine its semantic intended meaning. Both of them make use of McGee’s open-endedness requirement and the second one uses in addition Garson’s [19] local models for defining the validity of these rules. I argue that the success of both these arguments is relative to their semantic or infinitary assumptions, which could be easily discharged if the introduction rule for the universal quantifier is taken to be an infinitary rule, i.e., non-compact. Consequently, I reconsider the use of the 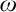$\omega $-rule and I show that the addition of the 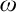$\omega $-rule to the standard formalizations of first-order logic is categorical. In addition, I argue that the open-endedness requirement does not make the first-order Peano Arithmetic categorical and I advance an argument for its categoricity based on the inferential conservativity requirement.

Keywords

categoricityinferentialismopen-endednesslocal modelsω-rule

MSC classification

Primary: 03A05: Philosophical and critical 03B10: Classical first-order logic 03B35: Mechanization of proofs and logical operations 03C35: Categoricity and completeness of theories 03C62: Models of arithmetic and set theory 03F03: Proof theory, general
Type
Article
Information
Bulletin of Symbolic Logic , Volume 30 , Issue 2 , June 2024 , pp. 227 - 252
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Belnap, N. D., Tonk, plonk and plink . Analysis , vol. 22 (1962), pp. 130–134.CrossRefGoogle Scholar
Bonnay, D. and Speitel, S. G. W., The ways of logicality: Invariance and categoricity, The Semantic Conception of Logic: Essays on Consequence, Invariance, and Meaning (G. Sagi and J. Woods, editors), Cambridge University Press, Cambridge, 2021, pp. 55–79.Google Scholar
Bonnay, D. and Westerståhl, D., Compositionality solves Carnap’s problem . Erkenntnis , vol. 81 (2016), no. 4, 721–739.CrossRefGoogle Scholar
Brandom, R., Articulating Reasons: An Introduction to Inferentialism , Harvard University Press, Cambridge, 2001.Google Scholar
Brîncuş, C. C., Are the open-ended rules for negation categorical? Synthese , vol. 198 (2021), pp. 7249–7256.CrossRefGoogle Scholar
Brîncuş, C. C., Inferential quantification and the omega rule, Perspectives on Deduction (A. P. d’Aragona, editor), Synthese Library Series, Springer, Gewerbestrasse, Switzerland, 2024.Google Scholar
Buldt, B., On RC 102-43-14 , Carnap Brought Home: The View from Jena (S. Awodey and C. Klein, editors), Open Court, Chicago and LaSalle, 2004, pp. 225–246.Google Scholar
Carnap, R., Logical Syntax of Language , K. Paul, Trench, Trubner, London, 1937.Google Scholar
Carnap, R., Introduction to Semantics , Harvard University Press, Cambridge, 1942.Google Scholar
Carnap, R., Formalization of Logic , Harvard University Press, Cambridge, 1943.Google Scholar
Chang, C. C. and Jerome, K., Model Theory , third ed., Dover Publications, Mineola, 2012.Google Scholar
Church, A., Review of Carnap 1943 . The Philosophical Review , vol. 53 (1944), no. 5, pp. 493–498.CrossRefGoogle Scholar
Dummett, M., The Logical Basis of Metaphysics , Harvard University Press, Cambridge, 1991.Google Scholar
Dunn, J. M. and Hardegree, G. M., Algebraic Methods in Philosophical Logic , Oxford University Press, Oxford, 2001.CrossRefGoogle Scholar
Fraenkel, A. A., Bar-Hillel, Y., and Levy, A., Foundations of Set Theory , second ed., Studies in Logic and the Foundations of Mathematics, vol. 67, Elsevier, Amsterdam, 1973.Google Scholar
Frazén, T., Transfinite progressions: A second look at completeness, this Journal, vol. 10 (2004), no. 3, pp. 367–389.Google Scholar
Garson, J., Categorical semantics , Truth or Consequences (J. M. Dunn and A. Gupta, editors), Springer, Dordrecht, 1990.Google Scholar
Garson, J., What Logics Mean: From Proof-Theory to Model-Theoretic Semantics , Cambridge University Press, Cambridge, 2013.CrossRefGoogle Scholar
Hardegree, G. M., Completeness and super-valuations , Journal of Philosophical Logic , vol. 34 (2005), pp. 81–95.CrossRefGoogle Scholar
Henkin, L., The completeness of the first-order functional calculus . The Journal of Symbolic Logic , vol. 14 (1949), no. 3, pp. 159–166.CrossRefGoogle Scholar
Hjortland, O. T., Speech acts, categoricity and the meaning of logical connectives . Notre Dame Journal of Formal Logic , vol. 55 (2014), no. 4, pp. 445–467.Google Scholar
Koslow, A., Carnap’s problem: What is it like to be a normal interpretation of classical logic? Abstracta , vol. 6 (2010), no. 1, pp. 117–135.Google Scholar
LeBlanc, H., Roeper, P., Thau, M., and Weaver, G., Henkin’s completeness proof: Forty years later . Notre Dame Journal of Formal Logic , vol. 32 (1991), no. 2, pp. 212–232.CrossRefGoogle Scholar
McGee, V., Everything , Between Logic and Intuition (G. Sher and R. Tieszen, editors), Cambridge University Press, Cambridge, 2000.Google Scholar
McGee, V., There’s a rule for everything , Absolute Generality (A. Rayo and G. Uzquiano, editors), Oxford University Press, Oxford, 2006, pp. 179–202.CrossRefGoogle Scholar
McGee, V., The categoricity of logic , Foundations of Logical Consequence (C. R. Caret and O. T. Hjortland, editors), Oxford University Press, Oxford, 2015.Google Scholar
Murzi, J., Classical harmony and separability . Erkenntnis , vol. 85 (2020), pp. 391–415.CrossRefGoogle ScholarPubMed
Murzi, J. and Hjortland, O. T., Inferentialism and the categoricity problem: Reply to Raatikainen . Analysis , vol. 69 (2009), no. 3, pp. 480–488.CrossRefGoogle Scholar
Murzi, J. and Topey, B., Categoricity by convention . Philosophical Studies , vol. 178 (2021), pp. 3391–3420.CrossRefGoogle ScholarPubMed
Peregrin, J., Rudolf Carnap’s inferentialism , The Vienna Circle in Czechoslovakia (R. Schuster, editor), Vienna Circle Institute Yearbook, vol. 23, Springer, Cham, 2020.CrossRefGoogle Scholar
Potter, M., Reason’s Nearest Kin: Philosophies of Arithmetic from Kant to Carnap , Oxford University Press, Oxford, 2000.CrossRefGoogle Scholar
Raatikainen, P., On rules of inference and the meanings of logical constants . Analysis , vol. 68 (2008), no. 300, pp. 282–287.CrossRefGoogle Scholar
de Rouilhan, P., Carnap on logical consequence for languages I and II , Carnap’s Logical Syntax of Language (P. Wagner, editor), Palgrave Macmillan, New York, 2009, pp. 121–146.CrossRefGoogle Scholar
Rumfitt, I., Yes and no . Mind , vol. 109 (2000), pp. 781–823.CrossRefGoogle Scholar
Scott, D., On engendering an illusion of understanding . The Journal of Philosophy , vol. 68 (1971), no. 21, pp. 787–807.CrossRefGoogle Scholar
Shoenfield, J. R., On a restricted $\omega$ -rule, L’Académie polonaise des sciences . Bulletin Série des Sciences Mathématiques, Astronomiques et Physiques , vol. 7 (1959), pp. 405–407.Google Scholar
Shoesmith, D. J. and Smiley, T. J., Multiple-Conclusion Logic , Cambridge University Press, Cambridge, 1978.CrossRefGoogle Scholar
Skolem, T., Über die nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen . Fundamenta Mathematicae , vol. 23 (1934), no. 1, pp. 150–161.CrossRefGoogle Scholar
Skolem, T., Peano’s axioms and models of arithmetic , Mathematical Interpretation of Formal Systems (T. Skolem, G. Hasenjaeger, G. Kreisel, A. Robinson, H. Wang, L. Henkin, and J. Łoś, editors), North-Holland, Amsterdam, 1955, pp. 1–14.Google Scholar
Smiley, T. J., Rejection . Analysis , vol. 56 (1996), no. 1, pp. 1–9.CrossRefGoogle Scholar
Smith, P., An Introduction to Gödel’s Theorems , 2nd edn. Cambridge: Cambridge University Press, 2013.CrossRefGoogle Scholar
Smullyan, R. M., First-Order Logic , Dover Publications, New York, 1968/1995.CrossRefGoogle Scholar
Warren, J., Shadows of Syntax: Revitalizing Logical and Mathematical Conventionalism , Oxford University Press, Oxford, 2020.CrossRefGoogle Scholar
Warren, J., Infinite reasoning . Philosophy and Phenomenological Research , vol. 103 (2021), no. 2, pp. 385–407.CrossRefGoogle Scholar