Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-21T18:28:10.405Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INTRODUCTION TO THE SCOTT COMPLEXITY OF COUNTABLE STRUCTURES AND A SURVEY OF RECENT RESULTS

Part of: Model theory Computability and recursion theory

Published online by Cambridge University Press:  15 November 2021

MATTHEW HARRISON-TRAINOR
MATTHEW HARRISON-TRAINOR*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MICHIGAN EAST HALL ANN ARBOR, MI 48109, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Every countable structure has a sentence of the infinitary logic 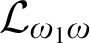$\mathcal {L}_{\omega _1 \omega }$ which characterizes that structure up to isomorphism among countable structures. Such a sentence is called a Scott sentence, and can be thought of as a description of the structure. The least complexity of a Scott sentence for a structure can be thought of as a measurement of the complexity of describing the structure. We begin with an introduction to the area, with short and simple proofs where possible, followed by a survey of recent advances.

Keywords

computable structure theoryScott rank

MSC classification

Primary: 03D45: Theory of numerations, effectively presented structures
Secondary: 03C57: Effective and recursion-theoretic model theory 03C70: Logic on admissible sets
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 28 , Issue 1 , March 2022 , pp. 71 - 103
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvir, R., Greenberg, N., Harrison-Trainor, M., and Turetsky, D., Scott complexity of countable structures. The Journal of Symbolic Logic, 2021, DOI: 10.1017/jsl.2021.4.Google Scholar
Alvir, R., Knight, J. F., and McCoy, C., Complexity of Scott sentences . Fundamenta Mathematicae, vol. 251(2020), no. 2, pp. 109–129.Google Scholar
Ash, C., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures . Annals of Pure and Applied Logic, vol. 42(1989), no. 3, pp. 195–205.CrossRefGoogle Scholar
Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , vol. 144, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 2000.Google Scholar
Baldwin, J. T., Friedman, S. D., Koerwien, M., and Laskowski, M. C., Three red herrings around Vaught’s conjecture . Transactions of the American Mathematical Society, vol. 368(2016), no. 5, pp. 3673–3694.Google Scholar
Becker, H., Strange structures from computable model theory . Notre Dame Journal of Formal Logic, vol. 58(2017), no. 1, pp. 97–105.CrossRefGoogle Scholar
Becker, H., Assigning an isomorphism type to a hyperdegree . The Journal of Symbolic Logic, vol. 85(2020), no. 1, pp. 325–337.CrossRefGoogle Scholar
Calvert, W., The isomorphism problem for classes of computable fields . Archive for Mathematical Logic, vol. 43(2004), no. 3, pp. 327–336.Google Scholar
Calvert, W., Fokina, E., Goncharov, S. S., Knight, J. F., Kudinov, O., Morozov, A. S., and Puzarenko, V., Index sets for classes of high rank structures . The Journal of Symbolic Logic, vol. 72(2007), no. 4, pp. 1418–1432.Google Scholar
Calvert, W., Harizanov, V. S., Knight, J. F., and Miller, S., Index sets of computable models . Algebra i Logika, vol. 45(2006), no. 5, pp. 538–574, 631–632.Google Scholar
Calvert, W. and Knight, J. F., Classification from a computable viewpoint. this Journal, vol. 12(2006), no. (2), pp. 191–218.Google Scholar
Calvert, W., Knight, J. F., and Millar, J., Computable trees of Scott rank $\ {\omega}_1^{CK}$ , and computable approximation . The Journal of Symbolic Logic, vol. 71(2006), no. 1, pp. 283–298.CrossRefGoogle Scholar
Carson, J., Harizanov, V., Knight, J., Lange, K., McCoy, C., Morozov, A., Quinn, S., Safranski, C., and Wallbaum, J., Describing free groups . Transactions of the American Mathematical Society, vol. 364(2012), no. 11, pp. 5715–5728.CrossRefGoogle Scholar
Chan, W., The countable admissible ordinal equivalence relation . Annals of Pure and Applied Logic, vol. 168(2017), no. 6, pp. 1224–1246.CrossRefGoogle Scholar
Chan, W., Bounds on Scott ranks of some Polish metric spaces. Journal of Mathematical Logic, vol. 21 (2021), no. 1, Paper No. 2150001, 23 pp.Google Scholar
Chan, W. and Chen, R., Bounds on continuous Scott rank . Proceedings of the American Mathematical Society, vol. 148(2020), no. 8, pp. 3591–3605.CrossRefGoogle Scholar
Chisholm, J., Effective model theory vs. recursive model theory . The Journal of Symbolic Logic, vol. 55(1990), no. 3, pp. 1168–1191.CrossRefGoogle Scholar
Cholak, P., Goncharov, S., Khoussainov, B., and Shore, R. A., Computably categorical structures and expansions by constants . The Journal of Symbolic Logic, vol. 64(1999), no. 1, pp. 13–37.CrossRefGoogle Scholar
Doucha, M., Scott rank of Polish metric spaces . Annals of Pure and Applied Logic, vol. 165(2014), no. 12, pp. 1919–1929.CrossRefGoogle Scholar
Doucha, M.. Erratum to: “Scott rank of Polish metric spaces” [Ann. Pure Appl. Logic 165 (12) (2014) 1919–1929] . Annals of Pure and Applied Logic, vol. 168(2017), no. 7, p. 1490.CrossRefGoogle Scholar
Downey, R. G., Kach, A. M., Lempp, S., Lewis-Pye, A. E. M., Montalbán, A., and Turetsky, D. D., The complexity of computable categoricity . Advances in Mathematics, vol. 268(2015), pp. 423–466.CrossRefGoogle Scholar
Freer, C. E., Models with high Scott rank , Ph.D. thesis, Harvard University, ProQuest LLC, Ann Arbor, MI, 2008.Google Scholar
Gao, S., Complexity ranks of countable models . Notre Dame Journal of Formal Logic, vol. 48(2007), no. 1, pp. 33–48.CrossRefGoogle Scholar
Gončarov, S. S., The number of nonautoequivalent constructivizations . Algebra i Logika, vol. 16(1977), no. 3, pp. 257–282, 377.Google Scholar
Gončarov, S. S. and Dzgoev, V. D., Autostability of models . Algebra i Logika, vol. 19(1980), no. 1, pp. 45–58, 132.Google Scholar
Harrison, J., Recursive pseudo-well-orderings . Transactions of the American Mathematical Society, vol. 131(1968), pp. 526–543.CrossRefGoogle Scholar
Harrison-Trainor, M., Scott ranks of models of a theory . Advances in Mathematics, vol. 330(2018), pp. 109–147.CrossRefGoogle Scholar
Harrison-Trainor, M., Describing finitely presented algebraic structures, preprint, 2020, http://www-personal.umich.edu/∼matthhar/papers/finitely-presented-structures.pdf.Google Scholar
Harrison-Trainor, M. and Ho, M.-C., On optimal Scott sentences of finitely generated algebraic structures . Proceedings of the American Mathematical Society, vol. 146(2018), no. 10, pp. 4473–4485.Google Scholar
Harrison-Trainor, M. and Ho, M.-C., Finitely generated groups are universal among finitely generated structures . Annals of Pure and Applied Logic, vol. 172(2021), no. 1, p. 102855.Google Scholar
Harrison-Trainor, M., Igusa, G., and Knight, J. F., Some new computable structures of high rank . Proceedings of the American Mathematical Society, vol. 146(2018), no. 7, pp. 3097–3109.CrossRefGoogle Scholar
Hirschfeldt, D. R., Khoussainov, B., and Shore, R. A., A computably categorical structure whose expansion by a constant has infinite computable dimension . The Journal of Symbolic Logic, vol. 68(2003), no. 4, pp. 1199–1241.CrossRefGoogle Scholar
Ho, M.-C., Describing groups . Proceedings of the American Mathematical Society, vol. 145(2017), no. 5, pp. 2223–2239.Google Scholar
Kleene, S. C.. On the forms of the predicates in the theory of constructive ordinals. II . American Journal of Mathematics, vol. 77(1955), pp. 405–428.CrossRefGoogle Scholar
Knight, J., Montalbán, A., and Schweber, N., Computable structures in generic extensions . The Journal of Symbolic Logic, vol. 81(2016), no. 3, pp. 814–832.CrossRefGoogle Scholar
Knight, J. F. and McCoy, C., Index sets and Scott sentences . Archive for Mathematical Logic, vol. 53(2014), nos. 5–6, pp. 519–524.CrossRefGoogle Scholar
Knight, J. F. and Millar, J., Computable structures of rank $\ {\omega}_1^{CK}$ . Journal of Mathematical Logic, vol. 10(2010), nos. 1–2, pp. 31–43.CrossRefGoogle Scholar
Knight, J. F. and Saraph, V., Scott sentences for certain groups . Archive for Mathematical Logic, vol. 57(2018), nos. 3–4, pp. 453–472.CrossRefGoogle Scholar
Larson, P. B., Scott processes , Beyond First Order Model Theory (José Iovino, editors), CRC Press, Boca Raton, FL, 2017, pp. 23–76.CrossRefGoogle Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas . Fundamenta Mathematicae, vol. 57(1965), pp. 253–272.CrossRefGoogle Scholar
Makkai, M., An example concerning Scott heights . The Journal of Symbolic Logic, vol. 46(1981), no. 2, pp. 301–318.Google Scholar
Marker, D., An analytic equivalence relation not arising from a Polish group action . Fundamenta Mathematicae, vol. 130(1988), no. 3, pp. 225–228.CrossRefGoogle Scholar
Marker, D., Bounds on Scott rank for various nonelementary classes . Archive for Mathematical Logic, vol. 30(1990), no. 2, pp. 73–82.CrossRefGoogle Scholar
Marker, D.. Model Theory: An Introduction , vol. 217 , Graduate Texts in Mathematics, Springer-Verlag, New York, 2002.Google Scholar
Marker, D.. Lectures on Infinitary Model Theory , volume 46, Lecture Notes in Logic, Association for Symbolic Logic, Chicago, IL; Cambridge University Press, Cambridge, 2016.Google Scholar
McCoy, C. and Wallbaum, J., Describing free groups, Part II: $\ {\varPi}_4^0 $ hardness and no $ {\varSigma}_2^0$ basis . Transactions of the American Mathematical Society, vol. 364(2012), no. 11, pp. 5729–5734.CrossRefGoogle Scholar
Melnikov, A. G. and Nies, A., The classification problem for compact computable metric spaces , The Nature of Computation , vol. 7921 (Paola Bonizzoni, Vasco Brattka and Benedikt Löwe, editors), Lecture Notes in Computer Science, Springer, Heidelberg, 2013, pp. 320–328.Google Scholar
Millar, J. and Sacks, G. E., Atomic models higher up . Annals of Pure and Applied Logic, 155(2008), no. 3, pp. 225–241.CrossRefGoogle Scholar
Miller, A. W., On the Borel classification of the isomorphism class of a countable model . Notre Dame Journal of Formal Logic, vol. 24(1983), no. 1, pp. 22–34.CrossRefGoogle Scholar
Miller, D. E., The invariant $ {\varPi}_{\alpha}^0 $ separation principle . Transactions of the American Mathematical Society, vol. 242(1978), pp. 185–204.Google Scholar
Montalbán, A., A computability theoretic equivalent to Vaught’s conjecture . Advances in Mathematics, vol. 235(2013), pp. 56–73.CrossRefGoogle Scholar
Montalbán, A., A robuster Scott rank . Proceedings of the American Mathematical Society, vol. 143(2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Montalbán, A., Effectively existentially-atomic structures , Computability and Complexity (A. Day, M. Fellows, N. Greenberg, B. Khoussainov, A. Melnikov, and F. Rosamond, editor), Springer, Cham, 2017, pp. 221–237.CrossRefGoogle Scholar
Montalbán, A., Computable Structure Theory: Beyond the Arithmetic, Draft.CrossRefGoogle Scholar
Morley, M., The number of countable models . The Journal of Symbolic Logic, vol. 35(1970), pp. 14–18.CrossRefGoogle Scholar
Nadel, M., Scott sentences and admissible sets . Annals of Mathematics Logic, vol. 7(1974), pp. 267–294.CrossRefGoogle Scholar
Nies, A., Describing groups. this Journal, vol. 13(2007), no. 3, 305–339.Google Scholar
Paolini, G., Computable Scott sentences for quasi-Hopfian finitely presented structures, preprint, 2020, arXiv:2010.13167.Google Scholar
Sacks, G. E.. On the number of countable models , Southeast Asian Conference on Logic (Singapore, 1981), vol. 111 (Chi Tat Chong and Malcolm John Wicks, editors), Studies in Logic and the Foundations of Mathematics. North-Holland, Amsterdam, 1983, pp. 185–195.CrossRefGoogle Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Sacks, G. E., Bounds on weak scattering . Notre Dame Journal of Formal Logic, vol. 48(2007), no. 1, pp. 5–31.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , Theory of Models (Proceedings of the 1963 International Symposium at Berkeley) (J. W. Addison, Leon Henkin, Alfred Tarski, editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Silver, J. H., Counting the number of equivalence classes of Borel and Coanalytic equivalence relations . Annals of Mathematical Logic, vol. 18(1980), no. 1, pp. 1–28.CrossRefGoogle Scholar
Turetsky, D., Coding in the automorphism group of a computably categorical structure . Journal of Mathematical Logic, vol. 20(2020), p. 2050016.Google Scholar
Vaught, R. L.. Denumerable models of complete theories , Infinitistic Methods (Proceedings of the Symposium on Foundations of Mathematics. Warsaw, 2–9 September 1959), Pergamon, Oxford; Państwowe Wydawnictwo Naukowe, Warsaw, 1961, pp. 303–321.Google Scholar
Wadge, W. W., Reducibility and determinateness on the Baire space , Ph.D. thesis, University of California, Berkeley, ProQuest LLC, Ann Arbor, MI, 1983.Google Scholar
Yaacov, I. B., Doucha, M., Nies, A., and Tsankov, T., Metric Scott analysis . Advances in Mathematics, vol. 318(2017), pp. 46–87.CrossRefGoogle Scholar