Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T06:01:38.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Accessible Recursive Functions

Published online by Cambridge University Press:  15 January 2014

Stanley S. Wainer
Stanley S. Wainer*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UkE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The class of all recursive functions fails to possess a natural hierarchical structure, generated predicatively from “within”. On the other hand, many (proof-theoretically significant) sub-recursive classes do. This paper attempts to measure the limit of predicative generation in this context, by classifying and characterizing those (predictably terminating) recursive functions which can be successively defined according to an autonomy condition of the form: allow recursions only over well-orderings which have already been “coded” at previous levels. The question is: how can a recursion code a well-ordering? The answer lies in Girard's theory of dilators, but is reworked here in a quite different and simplified framework specific to our purpose. The “accessible” recursive functions thus generated turn out to be those provably recursive in (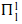 –CA)0.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 5 , Issue 3 , September 1999 , pp. 367 - 388
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Arai, T., A slow growing analogue of Buchholz' proof, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 101–120.Google Scholar
[2] Buchholz, W., An independence result for ( – CA) + (BI), Annals of Pure and Applied Logic, vol. 32 (1987), pp. 131–155.Google Scholar
[3] Buchholz, W., Cichon, E. A., and Weiermann, A., A uniform approach to fundamental sequences and subrecursive hierarchies, Mathematical Logic Quarterly, vol. 40 (1994), pp. 273–286.Google Scholar
[4] Buchholz, W., Feferman, S., Pohlers, W., and Sieg, W., Iterated inductive definitions and subsystems of analysis, Lecture Notes in Mathematics, no. 897, Springer-Verlag, Berlin, 1981.Google Scholar
[5] Fairtlough, M. and Wainer, S. S., Hierarchies of provably recursive functions, Handbook of proof-theory (Buss, S., editor), Studies in Logic, no. 137, North-Holland, Amsterdam, 1998, pp. 149–207.Google Scholar
[6] Feferman, S., Three conceptual problems that bug me, to appear in the Proceedings of the 7th Scandinavian Logic Symposium, Uppsala 1996.Google Scholar
[7] Girard, J-Y., -logic, Part I: Dilators, Annals of Mathematical Logic, vol. 21 (1981), pp. 75–219.Google Scholar
[8] Kadota, N., On Wainer's notation for a minimal subrecursive inaccessible ordinal, Mathematical Logic Quarterly, vol. 39 (1993), pp. 217–227.Google Scholar
[9] Rathjen, M., How to develop proof-theoretic ordinal functions on the basis of admissible ordinals, Mathematical Logic Quarterly, vol. 39 (1993), pp. 47–54.CrossRefGoogle Scholar
[10] Schmidt, D., Built-up systems of fundamental sequences and hierarchies of number-theoretic functions, Arkiv für Math. Logic und Grundlagenforschung, vol. 18 (1976), pp. 47–53.Google Scholar
[11] Vauzeilles, J., Functors and ordinal notations IV: The Howard ordinal and the functorΛ, this Journal, vol. 50 (1985), pp. 331–338.Google Scholar
[12] Wainer, S. S., Slow growing vs. fast growing, this Journal, vol. 54 (1989), pp. 608–614.Google Scholar
[13] Wainer, S. S., Accessible segments of the fast growing hierarchy, Proceedings of logic colloquium 95, Haifa (Makowsky, J. and Ravve, E., editors), Lecture Notes in Logic, no. 11, Springer-Verlag, Berlin, 1998, pp. 339–348.Google Scholar