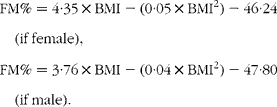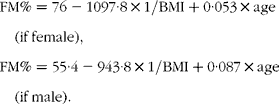The relative contribution of fat-free mass (FFM) and fat mass (FM) to body weight is a relevant indicator for major public health issues(Reference Snijder, van Dam and Visser1, Reference Bender, Trautner and Spraul2). Due to the accumulation of excess fat tissue, the worldwide increase in the prevalence of obesity contributes to a high risk of metabolic disorders such as CVD and type 2 diabetes(Reference Flegal and Graubard3). In addition, FFM loss in ageing populations and its progression towards sarcopenia increase morbidity and mortality(Reference Gallagher, Ruts and Visser4–Reference Rolland, Czerwinski and Abellan Van Kan6). Accurate measurements of body composition can be obtained from reference methods, such as underwater weighing, dilution techniques and dual-energy X-ray absorptiometry (DXA). Although the use of such methods is widespread, their application is time consuming and expensive, and as a result, they are not relevant for use as a part of routine clinical examinations or population studies. Bioelectrical impedance has often been considered to be a convenient tool for body composition analysis. However, the recorded bioelectrical values (resistance and reactance) must be used in equations that are body shape specific, and accurate FFM and FM assessments require adjustments with a gold standard method(Reference Janssen, Heymsfield and Baumgartner7–Reference Kyle, Bosaeus and De Lorenzo10).
In contrast, simple anthropological measurements, such as body weight or BMI, cannot give a reliable quantification of body composition, although they are of predictive interest at a population level(Reference Flegal and Graubard3, Reference Gallagher, Heymsfield and Heo11–Reference Duggleby, Jackson and Godfrey13). Models that provide reliable predictions of body composition from very simple covariables are still needed. Because increasingly more information on body composition analysis is available, either directly from large surveys (e.g. National Health and Nutrition Examination Survey; NHANES) or indirectly through scientific publications, we investigated the potential of a non-parametric model derived from a Bayesian network (BN) to predict body composition. A BN provides a global joint probability distribution over a set of random variables(Reference Carlin and Louis14, Reference Albert, Grenier and Denis15). The ability to combine variables and the growing capabilities of computer calculations have made these models increasingly popular. Indeed, they have become of great use in quantitative risk assessment(Reference Albert, Grenier and Denis15–Reference Jeanpierre and Charpillet17). However, to our knowledge, such models have not been used for body composition analysis. Assuming a direct influence of sex, age, body weight and height on body composition(Reference Ellis18–Reference Jackson, Ellis and McFarlin21), we hypothesised that it might be possible to assess the body composition of any subject by selecting an adjusted FFM value from a DXA measurement database (DXA, 1999–2004 NHANES) with easily accessible covariables (sex, age, height and weight). The present study aims to present this new calculation concept and to validate BN predictions for FFM and FM against DXA measurements obtained from an independent sample of French subjects. A comparison with previously published linear models(Reference Gallagher, Heymsfield and Heo11, Reference Jackson, Stanforth and Gagnon22) was also performed.
Method
Reference database used for body composition analysis
All FFM values used for body composition predictions were extracted from the NHANES website (http://www.cdc.gov/nchs/about/major/nhanes/) for the 1999–2004 period (n 10 402). Subjects were characterised from the covariables (sex, age, height and weight) included in the model irrespective of ethnicity (Table 1).
Table 1 Population description in the databases used as the reference (National Health and Nutrition Examination Survey (NHANES)), for model adjustment (CHU-fit) and for validation (CHU-valid)
(Mean values and standard deviations)

CHU, Clermont-Ferrand University Hospital Centre; FFM, fat-free mass; FM, fat mass.
* Mean values were significantly different between NHANES and CHU (valid or fit) within a sex group (P < 0·001).
† Mean values were significantly different between CHU-fit and CHU-valid (P < 0·001).
For the current purpose, only subjects having a valid scan were included, and the mean value of five DXA measurements (Hologic QDR-4500) was considered. Lean mass values were increased by 5 % to overcome the initial reduction imposed on the entire NHANES database, as explained in the user guide (http://www.cdc.gov/nchs/nhanes/dxx/dxa.htm)(Reference Schoeller, Tylavsky and Baer23).
Independent body composition database for model fitting and validation
A database of 1140 French subjects (aged between 20 and 79 years and with BMI between 18·5 and 40 kg/m2) who had their body composition measured by DXA (Hologic QDR-4500) during routine examination at the Radiology Department of the Clermont-Ferrand University Hospital Centre (CHU) between 1998 and 2008 was used. From this database, two different subsets were defined to adjust parameters for FFM estimates (CHU-fit: 380 subjects), and the second was used to cross-validate model responses (CHU-valid: 760 subjects) (Table 1). Subsets were matched for sex and BMI distributions.
Fat-free mass adjustments
For each subject in the CHU-fit database, a subset of candidates was selected in the NHANES database using a BN equation, which included the age, body weight and height of the subject to predict.
A distance was computed from the covariables using the following formula:
where d a, d h, d w are the absolute values of the difference for age, height and weight, respectively, between the CHU subject to predict and the NHANES subjects of similar sex, and w a, w h, w w are associated weighting parameters for age, height and weight, respectively. A maximal distance (D m) was defined as the maximal selection limit. Only the NHANES subjects with D < D m were retained as candidates for prediction. When the closest NHANES subject was at a distance greater than D m, the predictive subset was empty, and no prediction was proposed.
For some combination of parameters (w a, w h, w w, D m), the coefficient of determination between FFM predictions and the corresponding DXA measurements, the standard error of prediction (SEP) and the prediction rate (ratio of the predicted individuals to the total number of individuals to predict) were simultaneously computed and used as criteria to estimate the quality of adjustment. Weighting parameters varying from 0·05 to 0·2 (age in years), 0·2 to 0·4 (height in cm) and 0·7 to 0·9 (weight in kg) were tested, with D m varying from 0·005 to 0·015 (arbitrary units). From a selected subset of candidates, the one having the median FFM value was used for prediction, and his/her FFM value was attributed to the CHU subject. Prediction was supported by the subject having the median FFM value of the subset of candidates instead of using the mean FFM value, which did not correspond to any particular subject. Increasing the number of candidates within the predictive subset extended the calculation process without producing a gain on the quality of prediction; thus, when the number of candidates exceeded fifty, only the fifty closest were kept. FM was then determined, assuming FM = body weight − FFM.
Extreme anthropometric situations were discarded, and model predictions were limited to subjects with BMI values between 18·5 and 40 kg/m2. In addition, model predictions were limited to subjects above 20 years of age to avoid growth influences on body composition analysis and below 79 years of age due to the weak representation of older subjects in the reference database. These restrictions were applied to the French databases (CHU-fit and CHU-valid) but not to the NHANES database. A candidate could be selected outside these limits when his/her covariables gave a distance below D m.
Comparisons with other predictive models
Predictions of the percentage of body fat (FM%) on CHU subjects were compared when obtained with either BN or multiple regression models. Two equations were considered as follows:
A predictive equation including sex and BMI(Reference Jackson, Stanforth and Gagnon22)
(1)
A predictive equation including sex, BMI and age(Reference Gallagher, Heymsfield and Heo11)
(2)
This last formula was proposed with an ethnic correction for Asian subjects, which was not used here. These equations were developed to predict FM%. Using a two-compartment model, they were applied to body weight to deduce FM and, consequently, FFM.
Statistical computations and analyses
Underlying calculations were processed using the Rebastaba package(Reference Denis, Delignette-Müller and Pouillot24) written in R (R Development Core Team, 2009), a language and environment for statistical computing (R Foundation for Statistical Computing, Vienna, Austria; ISBN 3-900051-07-0, URL http://www.R-project.org), which is available at http:/r-forge.r-project.org/projects/riskassessments/
The quality of prediction was globally assessed on both CHU-fit and CHU-valid databases by the SEP, which is defined as follows:

where n is the number of subjects in the corresponding database.
Differences between population characteristics were analysed with Student's t test (XLstat 2008). Correlations between variables were calculated with Pearson's formula.
Results
Model parameter adjustments
The NHANES and CHU (fit and valid) subjects were significantly different for all variables (P < 0·001) with the exception of height (except for CHU-valid, where women were taller than those in the other groups). The NHANES subjects had greater body weight, BMI and FM than the French subjects. The CHU subjects had a slightly but significantly higher FFM (not significant for CHU-fit women) than the NHANES subjects. CHU-valid women had higher FFM values than the other female groups (Table 1). Therefore, BN prediction was analysed for subjects very distinct from the NHANES population.
Numerous combinations of weighting coefficients and D m were first considered. Among them, 125 effective combinations were scrutinised for the SEP and rate of prediction for the subjects belonging to the CHU-fit database. As expected, there were interactions between the SEP and the rate of prediction. The SEP decreased with D m until a minimum corresponding to the optimal fit between FFM predictions and DXA measurements, and then increased again with larger D m values (Fig. 1(a)). Decreasing D m led to an increase in the number of empty predictive subsets and consequently worsened the prediction rate. Reaching a predictive rate of 100 % was possible but reduced the quality of fit (SEP approximately 3 kg; Fig. 1(b)). The retained combination provided a compromise between the two criteria, with an SEP of 2·84 kg and a prediction rate of 99·21 %. The corresponding weighting parameters were as follows:
with D m set at 0·0075.

Fig. 1 Variation of the standard error of prediction (SEP) over the tested combinations of parameters: (a) when varying the maximal distance (D m) used in the Bayesian network prediction (arbitrary units) and (b) its covariation with the rate of prediction.
Using these weighting parameters, the correlation between FFM predicted by the BN equation and FFM measured by DXA for the CHU-fit subjects was highly significant (R 2 0·94, P < 0·001). This combination of parameters was used in all subsequent calculations.
Accuracy of model prediction
The BN equation was cross-validated on the CHU-valid subjects. The subjects' repartition was fairly balanced between the CHU-fit and CHU-valid groups. No difference was observed for variables from men from the two databases. However, CHU-valid women were slightly taller and had higher FFM values than CHU-fit women. The covariables (age, height and weight) of the NHANES subjects selected as predictors were similar to those of the CHU subjects, and no difference was observed between the groups (Table 2).
Table 2 Population description for the CHU-valid subjects (n 760) and the National Health and Nutrition Examination Survey (NHANES) subjects used as predictors (n 760)*
(Mean values and standard deviations)

CHU, Clermont-Ferrand University Hospital Centre.
* There were no significant differences between groups stratified by sex (P>0·001).
The FFM, FM and FM% values of the predictors were plotted against their respective experimental DXA counterparts (Fig. 2). Accuracy of BN prediction was compared with the two linear models, equations 1 and 2. The quality of fit was excellent in women for FFM (SEP 2·71 kg, R 2 0·86) and was superior to those obtained with equation 1 (SEP 3·64 kg, R 2 0·82) or equation 2 (SEP 3·73 kg, R 2 0·83). Similar trends were found for males; however, discrepancies between the three models were less pronounced for males than for females. All correlations were highly significant (Table 3). Because FM was deduced from FFM, the SEP was equivalent for FFM and FM. Correlations were still highly significant for FM%, although predictions were less closely fit to their experimental counterparts, and the SEP remained lower for BN prediction than those obtained with linear models.

Fig. 2 Scatter plots of Bayesian network prediction for fat-free mass (FFM) (a), fat mass (FM) (b) and the percentage of FM (FM%) (c) in terms of their experimental counterparts derived from dual-energy X-ray absorptiometry measurements on CHU-valid men (●) and women ( × ). The first bisectors are drawn (- - -).
Table 3 Quality of fit between fat-free mass (FFM) and the percentage of fat mass (FM%) as measured by dual-energy X-ray absorptiometry with the CHU-valid subjects and their counterparts predicted by the Bayesian network (BN), equation 1(Reference Jackson, Stanforth and Gagnon22) and equation 2(Reference Gallagher, Heymsfield and Heo11) for men and women*

CHU, Clermont-Ferrand University Hospital Centre; SEP, standard error of prediction.
* All R 2 values were significant (P < 0·001).
When FM% was expressed in terms of BMI, a large inter-individual variability was observed with experimental measurements for both males and females. This variability was better described by the BN predictions than with other models (Fig. 3). The variability observed with equation 2 was introduced by the age effect, which was not sufficient by itself to describe the inter-individual variability. In contrast, the well-known sex difference in FM% in terms of BMI was well described by the three predictive models.

Fig. 3 Relationship between BMI and fat mass (FM), expressed as a percentage of body weight (FM%) measured by (a) dual-energy X-ray absorptiometry on CHU-valid men (●) and women ( × ) and the corresponding predictions for (b) the Bayesian network, (c) equation 1(Reference Jackson, Stanforth and Gagnon22) and (d) equation 2(Reference Gallagher, Heymsfield and Heo11). CHU, Clermont-Ferrand University Hospital Centre.
Discussion
The main objective of the present study was to investigate the potential use of a non-parametric equation derived from a BN to assess body composition with easily accessible covariables. BN are particularly useful in predicting events in a population when only part of the information is available or eventually provided as aggregated information. However, in the present study, BN prediction was validated in a context where all the covariables needed for prediction were known. It was shown that the BN enabled the precise prediction of the FFM of the French subjects (CHU) from body composition values recorded in the US population (NHANES). The first requirement in developing such a model was to have a validated database of body composition measurements. DXA is one of the gold standard methods for assessing body composition(Reference Heymsfield, Lohman and Wang25). The NHANES database, to our knowledge, is the largest database of DXA body composition measurements available for downloading. It offers a good reliability, with five replicates per subject recorded under validated procedures. The second requirement was to have a database of body composition analysis for a population similar to the population of interest. We were particularly interested in describing a French European population. Therefore, we used a French dataset to adjust the parameters of the BN equation. However, the equation could have been adjusted or applied to any other population. It is interesting to note that the NHANES database could be used to describe the body composition of a population of interest that differed in many aspects (age, weight and BMI). To predict the body composition of a subject, the BN equation returned an adjusted subset of candidates from which the one having the median FFM value was the predictor. His/her FFM value was attributed to the subject to predict, and FM was directly deduced as the body weight minus FFM. It would have been possible to do similar adjustments from any body compartment (fat, lean or bone mass). However, FFM was the most important body compartment, and the one most closely adjusted to the BN covariables(Reference Ellis18–Reference Deurenberg20). FM was then considered to be the adjusting variable. Bone mineral content represents the smallest compartment (about 3·5 % of weight). It was not considered to be a specific compartment but was included in FFM.
The potential outcomes associated with a reliable predictive model for body composition have been highlighted(Reference Snijder, van Dam and Visser1), and many attempts to describe body composition, particularly body fat, using linear models with simple variables have been proposed. They usually included BMI, and occasionally, age or ethnicity(Reference Deurenberg20, Reference Heymsfield, Lohman and Wang25, Reference Larsson, Henning and Lindroos26). It was thus interesting to compare the fit obtained with BN prediction and with linear predictive models when applied to the same population. Two robust and clearly described equations were used for comparison. Equation 1(Reference Jackson, Stanforth and Gagnon22) included a quadratic form of BMI that was irrespective of age, while equation 2(Reference Gallagher, Heymsfield and Heo11) included BMI, age and ethnicity, both with sex specificities. When applied to the CHU-valid subjects, the quality of FM% adjustments was very similar to those obtained in the original population context(Reference Gallagher, Heymsfield and Heo11, Reference Jackson, Stanforth and Gagnon22). For equation 2, the quality of fit varied from R 2 0·81, with SEP 4·31 %, in the original population to R 2 0·81, with SEP 4·01 %, for the CHU-valid subjects. For equation 1, when stratified by sex, the quality of fit varied from R 2 0·78, with SEP 4·63 %, in the original population to R 2 0·67, with SEP 4·73 %, for CHU-valid females and from R 2 0·68, with SEP 4·90 %, to R 2 0·59, with SEP 4·12 %, for CHU-valid males. The similarity of fit obtained with these two models in different populations confirms their robustness. For both body compartments (FFM and FM), BN prediction resulted in a better fit than linear models, especially for FFM, which was the adjusted compartment.
It is noteworthy that BN prediction was obtained without considering ethnicity. At first, ethnicity was included as a putative variable in the network due to its possible impact on FFM(Reference Gasperino, Wang and Pierson27, Reference Aloia, Vaswani and Feuerman28) and on fat deposition(Reference Lear, Humphries and Kohli29, Reference Kagawa, Kerr and Uchida30). In calculations not shown here, the quality of fit was analysed using either white, non-Hispanic subjects alone (as defined in the NHANES database) or all subjects, irrespective of ethnicity. Although the French population to predict (CHU) was mostly Caucasian, the best fit was obtained when the entire database was used (SEP 2·84 kg) rather than limited to white, non-Hispanic subjects (SEP 3·11 kg). The influence of ethnicity was, therefore, not included in the final model adjustment.
Sex differences observed in the relationships between BMI and FM% were similar to those previously described(Reference Jackson, Ellis and McFarlin21, Reference Flegal, Shepherd and Looker31). In contrast to other predictive linear models, BN prediction provided a stochastic picture of inter-individual variability, as illustrated by the relationship between BMI and FM% and could be useful to depict biological variability in any population of interest.
The BN equation is not a ready-to-use tool for straight application; instead, it should be considered as a new concept in the field of body composition assessments that can be improved in further releases. The applicability and accuracy of model predictions directly depend on the quality and quantity of the available information in the NHANES database. The predictive subset size varied from zero to fifty subjects. An empty subset meant that it was not possible to find a candidate in NHANES having the requested age, height and weight within the constraints imposed by the BN equation This prediction failure was rather low, and only four subjects out of 760 were not predicted. When the subset size equalled one, the FFM prediction was deduced from a single candidate with a higher risk of poor adjustment. These types of situations were more frequently found for extreme anthropometric values. Of the five predicted subjects with a subset of one (all female), two were taller than 180 cm, and two were shorter than 148 cm. Excluding subjects predicted from only one candidate, the quality of fit was slightly better for FFM (SEP 2·76 kg instead of 2·84 kg) but with a decreased rate of prediction (from 99·2 to 98·54 %). In contrast, a NHANES subject can be selected as a predictor for different CHU-valid subjects (six NHANES subjects were selected three times; sixty-seven were selected twice and 604 were involved in a single prediction). The number of replicates of a predictor depended on the covariable distribution of the population to predict. Retaining different model limits to avoid rare anthropometric situations could be a possible way to improve the model.
The quality of FFM predictions obtained with the BN model were similar to those obtained with bioelectrical impedance equations, where SEP varied from 2 to 3·6 kg(Reference Kushner32), suggesting that BN predictions could offer an interesting alternative to bioelectrical impedance measurements, usually considered as a convenient field measurement(Reference Lukaski, Johnson and Bolonchuk8). An additional interesting aspect of such a model derived from BN is the possibility of adding/removing variables. Waist circumference has a significant relationship with body fat(Reference Flegal, Shepherd and Looker31, Reference Boardley and Pobocik33). Thus, it might be worth considering its inclusion to improve the BN prediction of body composition.
Acknowledgements
The authors are grateful to Dr Ristori from the Radiology Department of the CHU for providing DXA data from the CHU database. The authors' responsibilities were as follows: L. M. was responsible for physiological statements, database collection and for writing the first draft of the manuscript. J.-B. D. and C. B. were responsible for model computations and statistics. L. M. and J.-B. D. designed the hypotheses. None of the authors had any conflict of interest regarding the manuscript. The present study was supported by a grant (ANSSD) from the INRA Human Nutrition Department, France.