A resurgence of interest has occurred in ‘Newton's method of approximation’ for deriving the roots of equations, as its repetitive and mechanical character permits ready computer use. If x = α is an approximate root of the equation f(x) = 0, then the method will in most cases give a better approximation as
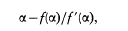
where f′(x) is the derivative of the function into which α has been substituted. Older books sometimes called it ‘the Newton–Raphson method’, although the method was invented essentially in the above form by Thomas Simpson, who published his account of the method in 1740. However, as if through a time-warp, this invention has migrated back in time and is now matter-of-factly placed by historians in Newton's De analysi of 1669. This paper will describe the steps of this curious historical transposition, and speculate as to its cause.