An idle student wandering the halls of the Sorbonne during the late 1840s, who just happened to enter the classroom of French geometer Michel Chasles (1793–1880), would have most likely stumbled upon chalkboards covered not only in figures, theorems and equations, but also in dates, quotations in Greek or Latin from ancient treatises, and various other historical remarks pertaining to the topic of the leçon du jour. If, their curiosity piqued, this student followed Chasles home, they would find the mathematician's abode to boast a labyrinthine library, its tortuous shelves covering wall upon wall with not only hundreds of mathematical treatises and journals, but also theological compendia, historical tomes on all subjects, and a plethora of rare manuscripts and autographs – valuable pieces whose attraction for Chasles, it is known, would later result in a misfortune most damaging to his international reputation.Footnote 1 If, finally, this student pored over the various papers scattered on Chasles's desk – ranging from brief notes hastily sketched at the back of a wedding invitation to carefully penned transcriptions of past public communications, destined to be printed by the publisher of the Académie des sciences – there again they would find those new equations whose construction Chasles had made the cornerstone of his new geometry side by side with puzzling attempts to trisect the angle or duplicate the cube, two classical problems from ancient Greece which, by no stretch of the imagination, could be deemed active research problems for a leading geometer of Chasles's time.
Chasles was hardly the first to bring historical narratives into the classroom or into mathematical treatises. In fact, many of the savants who designed and first taught at the new schools of the French Republic, including the École polytechnique where Chasles trained between 1812 and 1814, participated in this trend, and this was especially so amongst mathematicians. The academicians-turned-professors who populated these budding institutions shared a common epistemic ideal, perhaps most clearly theorized by Sylvestre Lacroix: the bounty of methods and concepts in their possession was not suited for teaching unless they first reorganized them in a natural and rational order and around a minimal set of general principles.Footnote 2 The case of mathematics was of particular importance to these savants: as Joan Richards has convincingly suggested, a conception of mathematics as the paradigmatic expression of l'esprit humain, stemming from Enlightenment philosophy, underlay Lacroix's treatises – and mathematical practice more widely in late eighteenth-century France.Footnote 3 And so many mathematicians, like Joseph-Louis Lagrange, incorporated historical discussions in their teaching. Beyond dates and bibliographical elements, the past thus mobilized by Lagrange was procured via what Amy Dahan-Dalmedico has called ‘a “deconstruction” of methods’, viz. epistemological analyses of past mathematical results and techniques aiming at uncovering the aforementioned rational order underlying them.Footnote 4 So great was the importance of these historical studies for Lagrange that he actively pushed for new editions and translations of ancient sources such as Diophantus’ Arithmetica.Footnote 5
Though Chasles was heir to this tradition, he pursued it in the context of newly emerging archival practices, and with his own mathematical and epistemological stakes in mind. First, Chasles held a strong commitment to the notion that the worth of a scientific method should be measured not just by the celerity with which it answers a given question, but by the clarity it brings to it – a goal for which, Chasles claimed, it was often useful (and sometimes necessary) to keep the most modern and expeditious methods at bay, and instead return to the insights of the more pedestrian geometry of the Ancients. Furthermore, all through his scientific career, Chasles sought to endow ‘pure geometry’ with inferential and expressive resources comparable in strength, fruitfulness and generality to those of ‘analysis’; that is to say, to make direct geometrical reasoning on figures alone as powerful as that couched in the language of Cartesian equations and algebraic computations – a programme he inherited from the students of Gaspard Monge, whose teaching of descriptive geometry at the École polytechnique was still extremely influential.Footnote 6 To demonstrate this claim and to carry out this programme, Chasles engaged continuously and jointly in both mathematics, viz. the rejuvenation of geometry, and historiography, viz. the writing of a long-term history of geometry aiming at highlighting the gradual shaping and progress of geometrical methods.
This essay explores a whole range of ways of gathering, enhancing and producing knowledge, collectively labelled ‘epistemic techniques’, all pertaining to the construction and ordering of the past, honed by Chasles through his historical writings, and then inventively mobilized in his geometrical treatises. In so doing, it shows that the development of Chasles's modern geometry crucially hinged upon a creative interweaving of archival, historical and mathematical work. Indeed, Chasles's historical research was not limited to the comfort of his vast library, nor to the meditation of commonly available treatises. It was often messy work, requiring frequent visits to archives, libraries and obscure Parisian booksellers and antiquarians, in a frantic hunt for lost treatises and rare sources. The fruit of these searches, we shall argue, can be directly observed in Chasles's mathematical output, thereby inviting a broadening of our understanding of the locales, modes of embodiment and tools of mathematical activity.
Practitioners of mathematics do not seem to belong in essential ways to any of such clearly identifiable sites of socially legitimate science, as laboratories, field stations, observatories, museums, botanical gardens and so on that have been thoroughly studied in recent years.Footnote 7 A more detailed approach, however, reveals that locality is no less central to the mathematical endeavour. Chasles's geometrical work will be shown to depend on circulations within a specific network of variously qualified spaces, viz. his own private study crammed with old books as a self-serving repository of printed culture, the Paris Royal Library and a few others across Europe for ancient manuscripts, the Académie des sciences and the Sorbonne for the purposes of exposition to different audiences.Footnote 8 In line with recent historical work focusing on the ways unnoticed, although pervasive, embodied processes underwrite knowledge making, all the more so efficiently when they thus contribute to creating allegedly disembodied knowledge, this paper will also portray how Chasles's work emerged from the entrenched heart-fluttering emotions in which Gaspard Monge saw the clear sign of a geometer's vocation, and the ‘archive fever’ that many of Michelet's contemporaries shared.Footnote 9 Furthermore, Chasles's apparently immaterial reworking of geometry required a great expenditure of unpublicized material toil in manuscript hunting and collecting first printed editions, sharp-eyed reading, collating, to-and-fro comparing, sequencing and organizing patiently excerpted data, reminiscent of older periods.Footnote 10 All these practices may help enlarge the historians’ view of the tools of knowledge beyond observation and measuring instruments, specimens and collections, or calculating and recording devices of all sorts. Eschewing ruinous divides between the scientific and the humanistic, this paper thus depicts a specific mathematical ‘life form’ predicated on the interweaving of the ancient and the modern, of traces of the past with promises for the future, an endeavour which thus fully constitutes a form of ‘science in the archives’.Footnote 11
Historiography as an epistemic technique: periodization and circulation
Chasles's first book, the 1837 Aperçu historique sur l'origine et le développement des méthodes en géométrie, was an avowedly teleological account of the development of some of the recent methods at the heart of ‘pure geometry’.Footnote 12 By retracing the inception of these ‘recent methods’, Chasles sought to display their capacity to ‘bring, in all the parts of the science of extension, a new facility and the means to reach a generalization theretofore unknown of all geometrical truths; which was also the proper character of Analysis, when it was applied to geometry’.Footnote 13 In other words, Chasles's surveying – and, indeed, use – of the past was intended for argumentative purposes removed from purely historical interests, something which appears clearly from the context for the writing of this book. Initially conceived as a response to a question posed in 1829 by the Royal Academy of Brussels regarding ‘the philosophical examination of the different methods of modern geometry’, Chasles's winning entry was then solely composed of two mathematical memoirs.Footnote 14 By 1837, these two memoirs had become the last third of a much more ambitious volume: its first third was the titular survey of geometrical methods proper, while its central section was composed of some twenty-six notes expanding on various technical aspects thereof – by way of either mathematical details, philosophical discussions or historical precisions. The transfigured scope and form of this book, and the lengthy period of time it took Chasles to compile and read sources in order to write it, point to an activity that cannot be explained away as the insatiable humanistic curiosity of a wealthy and independent savant. This labour was, in fact, fully directed toward improving the geometrical knowledge imparted by the proofs and theorems his memoirs already contained.
Within this labour, we shall distinguish two related epistemic techniques which grew out of the Lagrangian practice of method deconstruction, namely ‘periodization’ and ‘circulation’. Periodization refers here to the construction of a progressive sequence of historical stages, characterized by qualitative increases in abstraction and generality, while circulation refers to the practice of moving between historically important theorems identified as part of one same theory. Both techniques served to illustrate and guide the progress of geometrical methods in different ways: the first by uncovering the principles and forces driving scientific progress, and the second by ordering the various theorems and methods pertaining to a common geometrical figure, thereby yielding insight into the central principle of its theory.
Much like Condorcet's posthumous Esquisse d'un tableau historique des progrès de l'esprit humain, Chasles's historical narrative is constructed as a succession of ‘epochs’ (époques), the first of which being that of ancient (Greek) geometry, and the last that of early nineteenth-century reformers of pure geometry, beginning with Gaspard Monge. By constructing this narrative of epistemic progress, Chasles emphasized the upward trajectory of pure geometry, its increasing ability to rival analysis in terms of computational strength and generality, and its untapped resources for which the works of geometers past provided ample evidence.Footnote 15
It should be noted, however, that the progression depicted in Chasles's historical reconstruction is not entirely linear. For instance, the introduction of algebraic techniques into geometry by medieval Islamic authors is presented by Chasles as a temporary loss of abstraction (since their algebraic expressions refer to concrete lengths and not to abstract magnitudes like those allegedly manipulated by Greek geometers), but a loss that was deemed a historical necessity.Footnote 16 Furthermore, the succession of these epochs is not strictly chronological, in that they present important overlaps. For instance, whereas the third epoch opens with Descartes's 1637 Géométrie and ‘the application of algebra to the theory of curves’, the previous epoch covered the introduction of new geometrical approaches including Pascal's and Desargues's projective methods, which are all either contemporary or slightly posterior to Descartes's treatise.Footnote 17
Noticing these breaks in the chronological progression of Chasles's historical narrative, the Italian refugee and member of the Paris Académie des sciences Guglielmo Libri pounced on the occasion to attack what he viewed as a ‘somewhat arbitrary division’.Footnote 18 A historian of mathematics in his own right, Libri nonetheless approached the subject with radically different objectives: he sought to show that ‘the intellectual state of peoples is always linked to their moral and political state’.Footnote 19 When viewed through such historiographical lenses, the backward motions of Chasles's historical narrative could only appear as a sign of imprecision, viz. a failure to weave the temporality of scientific progress, with all its vagaries, into the presumably unyielding way of the political world. Chasles's organization of the past, by contrast, was indifferent to social or military history: it served first and foremost the identification of the epistemological and mathematical breaks that brought forth new levels of abstraction and generality.
His second epoch, for instance, describes a historical moment during which various European early modern mathematicians, ignoring algebra, nonetheless strove to introduce in pure geometry conceptions endowed with a degree of generality theretofore unseen. For instance, Chasles notes, whereas the application of Archimedes’ method of exhaustion ‘becomes, in each particular case, a wholly new question’, Roberval's method for the construction of tangents does not rely on the individual consideration of any specific curve.Footnote 20 Collectively, the geometers grouped in this second epoch enabled ‘a passage from concrete ideas to abstract ideas’ in a variety of geometrical questions.Footnote 21 Chasles's third epoch, in turn, focused on Descartes's introduction of the algebraic ‘instrument’ in the theory of curves; an epistemological and mathematical transformation radically different from that surveyed in the previous epoch for many reasons. Chasles famously contended that ‘no germ of Descartes's doctrine can be found in the writings of ancient geometers’, but also, and more importantly, that the gain in ‘universality’ that Descartes's invention brought into geometry differed in essence from that provided by Roberval's method.Footnote 22 By deriving properties from the equation of a curve, Chasles explained, Descartes could ‘establish, in a single formula, general properties of entire families of curves’.Footnote 23 In other words, Chasles mobilized a deconstruction à la Lagrange of Archimedes’, Roberval's, and Descartes's methods to identify two independent breaks in the history of geometry, both of which resulted in new kinds of generality.
The other epistemic technique at play in Chasles's historiography can be observed in his discussion of the geometry of conics in Notes XV and XVI. In each of these notes, Chasles focused on the ‘anharmonic property’ of, respectively, the points and the tangents of a conic. Proving the truth of these properties was easy enough for Chasles, who did so in but a few lines. The rest of these notes, however, was devoted to another task: that of proving their centrality and fruitfulness. Chasles's goal, here as in other parts of the Aperçu historique, was to highlight the importance of the concept of ‘anharmonic ratio’, both as a historical factor of mathematical progress and as a notion around which modern geometrical theories ought to be constructed. To that end, Chasles set out to show how all general theorems on conics can be obtained effortlessly as transformations of these dual anharmonic properties. The proof of his meta-mathematical claim came by way of a second epistemic technique, namely the circulation between and ordering of various historical results on these curves.
In Note XV, for instance, Chasles begins with what he understood to be Desargues's theorem on the involution of six points on a conic. The configuration associated with this theorem is that of a conic in which a quadrilateral ABCD is inscribed (viz. whose four vertices lie on the conic), and of a transversal line passing through a fixed point P (see Figure 1). Let us denote X and Y the two points at which this transversal intersects the conic. From two opposite vertices of the quadrilateral (for instance, B and D), Chasles drew the two straight lines passing through X and Y. Through both points D and B pass four lines, namely BA, BC, BX, BY and DA, DC, DX, DY. Each of these quadruplets of lines intersects the transversal at four points, namely F, G, X, Y and M, N, X, Y, thereby making for a total of six distinct points on the transversal. Desargues's involution theorem, as read by Chasles, states that the ‘anharmonic ratio’ of the first four points is equal to that of the four others, i.e.
$$\displaystyle{{FX} \over {FY}}\colon \displaystyle{{GX} \over {GY}} = \displaystyle{{MX} \over {MY}}\colon \displaystyle{{NX} \over {NY}}.$$
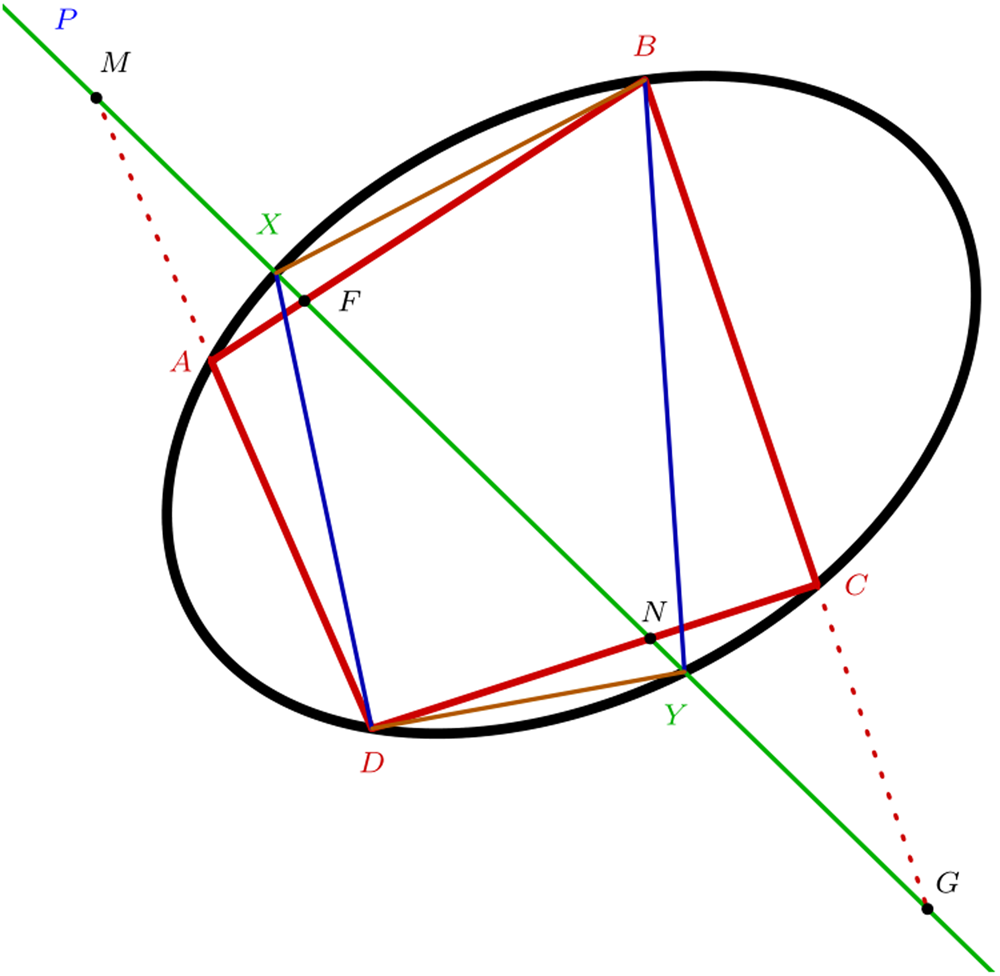
Figure 1. Desargues's involution (authors’ own drawing).
Having constructed the figure and the theorem corresponding to Desargues's theorem, Chasles then altered his viewpoint on them. Instead of the construction of six points on a transversal, between which a certain relation holds, Figure 1 can be viewed as the representation of a conic constructed by the intersection of the lines of two pencils. In other words, Chasles suggests considering the four lines passing through B and D as the lines of two pencils, between which a natural one-to-one correspondence exists: the rays that intersect on the conic (viz. BX and DX, BF and DM etc.) correspond to one another. Viewed in such a manner, the figure illustrates another property of conic sections, namely:
When two pencils of four lines are in a one-to-one correspondence, if the anharmonic ratio of the first four is equal to that of the four others, then the lines of a pencil will respectively meet the corresponding lines at four points, all of which will be on a conic section passing through the two bases of these pencils.Footnote 24
This new, general theorem, Chasles comments, is merely a reformulation of Desargues's, but one that has tremendous epistemic advantages over the latter. In particular, from this reformulation follows ‘an infinity of manners to generate conics via the intersection of two lines turning about two fixed points’.Footnote 25 In the rest of the note, Chasles goes over a collection of well-known historical results on conics, each of which appeared to be a mere transformation of that core result, thereby displaying in concreto the latter's central status in the theory of conics.
Newton's organic description of these curves, for instance, consisted in the rotation of two constant angles about two fixed points such that two paired legs of both these angles constantly intersect alongside a fixed straight line. The other two legs, Newton had shown, would then always intersect alongside a conic, on which the two fixed points lay. As Chasles demonstrated, this generation could simply be viewed as a particular case of the theorem stated above, obtained by transporting the two pencils into a specific configuration. And similarly, Pappus’ ad quatuor lineas theorem, a highly important result in the history of analytic geometry, as well as Pascal's ‘mystical hexagram’, could be obtained as two of the many forms that Chasles's general theorem could adopt.Footnote 26
Reading anew the texts of Pappus, Descartes or Newton revealed the fruitfulness of the concept of anharmonic ratio as a basis for the reorganization of all theorems about conics. These theorems, whilst equivalent from a logical standpoint, can all be derived with great ease from one of them, namely that expressed in terms of an equality between anharmonic ratios. Chasles's contention, as summarized by Karine Chemla, is that ‘equivalent formulations of the same fact … do not have the same generality’.Footnote 27
As the common source for a multitude of other results on conics, the theorem singled out by Chasles stands at the ‘centre’ of the theory of these curves, and therefore must be taken as its starting point.Footnote 28 At the beginning of this note, Chasles had given a ‘direct proof’ of this theorem in but a few lines.Footnote 29 To prove its centrality, however, Chasles had had to resort to a form of historical writing distinct from periodization, viz. a back-and-forth circulation between historical results. This historiographical practice was a key epistemic technique to obtain the sort of (geometrical) knowledge that Chasles actively sought. At various points in the Aperçu historique, Chasles put forth the notion that it is not enough to have theoretical instruments for the derivation of truths, so long as these do not provide explanations regarding the order of these truths.Footnote 30 As a result, Chasles's research practice consisted not only in deriving theorems, but also in reflecting about how to structure a theory, viz. searching for its fundamental principles, core concepts and methods. And in the conduct of this very search, this form of historical navigation proved to be an invaluable epistemic technique.
A material history of algebra
In a series of communications presented to the Académie des sciences between May and September 1841, Chasles extended the domain of his deconstructive techniques by applying them to the historiography of algebra.Footnote 31 This was essentially new ground for him, for he had only incidentally touched upon this subject in his Aperçu historique. The opportunity for this fresh line of enquiries had been provided by what he considered hasty and erroneous assertions recurrently made by Libri on Leonardo Pisano, also known as Fibonacci, and Viète. Chasles and Libri were rivals in both mathematical scholarship and expertise in ancient manuscripts, and so the matters of contention between them were many. Ever since the late 1830s, they had engaged in an indirect exchange of views by means of extended notes added to their respective main opuses, in which each of them took into account and mostly opposed the other's tenets. With respect to the history of algebra, they disagreed on two main scores. Whereas Libri averred that contrary to a common view, Diophantus should be denied any part in prefiguring this science, for the Indians alone should be credited with its invention, Chasles concurred with Lagrange in acknowledging Diophantus’ Arithmetica as one of the due sources of algebra.Footnote 32 More central to our present purpose, they also disagreed about the very nature of algebraic notations and operations, and hence the proper assessment of Fibonacci's and Viète's respective contributions to the history of algebra.
In an extended note to the second volume of his Histoire des mathématiques en Italie, Libri had provided the first Latin edition of what he presented as Fibonacci's algebra; that is, the fifteenth chapter of the Liber Abaci (1202), which he had transcribed from an Italian manuscript kept in Florence.Footnote 33 However, on the basis of this editorial work on the primary sources, Libri drew conclusions which Chasles found ill-conceived and misguided:
Mathematically speaking, [Chasles claimed,] it is quite inexact to say that Fibonacci performed algebraic operations upon letters, absolutely in the same way as it is done at present; this is mixing up two essentially different things, viz. the reasoning upon letters, and the calculation carried out upon or symbolized by these letters; it is mixing up numerical algebra, the only one cultivated by Fibonacci, with specious or literal algebra, invented by Viète and in use at present.Footnote 34
Chasles's central insight amounted to fully acknowledging this difference, which in return provided him with a criterion for applying his deconstructive techniques of periodization and circulation to the historiography of algebra. In this way, not only were historical stages discernible, but such enhanced historical understanding would also prove an effective driving force for pursuing geometry.
In order to counter Libri's contention, Chasles explained what Fibonacci really did, which, properly speaking, included no hint of ‘algebraic operations’. In so doing, he ventured on Libri's turf and scored points where the latter thought he reigned supreme. Arguments from authority could be met by demonstrations of better access to rare manuscripts. Libri had based his edition of the fifteenth chapter of Fibonacci's Liber Abaci on one complete manuscript kept at the Magliabechiana Library in Florence, with incidental forays in a few others, all incomplete and Florentine. In reply, Chasles mentioned three further Parisian manuscripts, kept at the Bibliothèque royale and the Mazarine Library, which he claimed were all more correct than the Magliabechian one.Footnote 35 More than a decade later, Baldassare Boncompagni compared and compiled all the extant manuscripts of Fibonacci's opus in order to yield a complete edition of the treatise, ever since deemed authoritative.Footnote 36 He would then give credit to Chasles for being the first to call attention to the three Parisian manuscripts.
The debate, however, did not exclusively revolve around ancient codices. In addition to his being able to check Libri's edition by also having direct access to the sources, Chasles essentially adduced mathematical grounds in support of his main point:
Fibonacci only knew how to perform [calculations] on numbers, as everyone did, and by no means upon letters, as is done now under the name of algebraic operations. For, while making use of letters, Fibonacci stands by the reasoning, and never let them enter into a symbolic formula [formule figurée]; he never expresses by means of the sole literal quantities that are proposed the successive operations that one would have to carry out upon these quantities to solve the question; these operations, he only knows how to describe in ordinary language, and their partial results, he represents by other auxiliary letters, foreign to the givens and to the unknowns of the question; which is essentially contrary to the spirit of Viète's algebra.Footnote 37
As an example, Chasles pointed to the way Fibonacci would prove the property which, for any two numbers a and b, would be expressed by the algebraic formula
$$a^2 + b^2 = ab\left({\displaystyle{a \over b} + \displaystyle{b \over a}} \right).$$While phrasing the procedure in ordinary language, Fibonacci symbolized neither the squares, nor the product, nor the quotients, but had recourse to fresh auxiliary letters at each and every step in the course of his reasoning. In Chasles's view, this use of letters to designate objects either wholly undetermined or connected with one another by definite relations of position, order or magnitude could be traced back to Greek geometry. Hence Fibonacci essentially belonged to the same stage (or epoch) as Euclid, Archimedes or Pappus.
Libri had wrongly discerned an essential turning point in Fibonacci's work, Chasles therefore concluded, for it lacked the very means that could permit one to symbolize algebraic operations. The ultimate meaning of what Viète had achieved in his In artem analyticem Isagoge (1591) thus required further elucidation. ‘Zetetics’, Viète had claimed, ‘no longer limited its reasoning [suam logicam] to numbers, a shortcoming of the old analysts, but worked with a newly discovered symbolic logistic [logistica speciosa] which was far more fruitful and powerful than numerical logistic for comparing magnitudes with one another’.Footnote 38 Chasles's understanding of what constituted the core of Viète's innovation grew from an incidental observation by Lacroix, whom he therefore credited for having sharply perceived the essential difference between ‘ancient algebra’ and Viète's new logistica speciosa. In Lacroix's interpretation,
Viète had felt that the reasonings serving to discover the series of operations to be carried out upon the givens of the problem could be made independent of these givens, by preventing these to mix with one another, and, so to speak, to merge into one another, by the arithmetical calculations. He extended to the designation of known quantities, the use of letters, which, so it seems, had been adopted, before him, for that of unknown quantities only.Footnote 39
Significant here is the emphasis placed on the givens and the knowns, for this shift proved decisive in setting Chasles's deconstructive reading in motion. The next step would consist in making clear how Viète introduced new notational resources in order to disentangle the series of operations from the givens and the knowns, and hence to represent the former apart from the latter by creating a symbolic language for this purpose. In Chasles's view, Libri severely distorted the meaning of Viète's invention by assuming that it was merely about notations, while completely overlooking the central issue of operations. As Chasles pointedly recalled, Diophantus already had represented the unknowns with some kind of symbols, something which Viète himself fully acknowledged. Properly conceived, however, symbols were more than mere notations, and actually supported algebraic operations. In Diophantus’ usage, operations were never severed from the givens, and to do so in the absence of a symbolic logistic, Viète commented, required a great amount of ingenuity. Chasles followed this suggestion in order to make completely explicit the essential properties which would make Viète's logistica speciosa into a fully fledged algebraic symbolism.
Viète's genuine innovation amounted to using letters for known quantities rather than for unknown ones, hence introducing undetermined coefficients with which it became possible to operate so that ‘virtual calculations’ could be symbolized by means of the composition of these coefficients. As these calculations were only registered in symbolic expressions and not actually carried out, the results of these calculations would also present themselves as ‘virtually given’.Footnote 40 This notion of virtual givenness would then prove pivotal in Chasles's deconstructive approach, in particular in his successful attempt at circulating it across domains. Detached from its original locus, viz. Viète's algebraic symbolism, this mathematical gesture would be reframed and transposed into pure geometry, historiography being the operative force in creating these new bridges.
In his protracted arm-wrestling with Libri, Chasles also adduced the judgement of the British historian Henry Hallam (1777–1859), later depicted as the initiator of a ‘Whig’ interpretation of history. Since he offered ammunition to counter Libri's glorification of the Italian algebraists at the expense of Viète, Chasles strategically made him the arbiter of their historiographical dispute.
Hallam indeed claimed that Viète should be given pride of place for being the first to apply letters as ‘general symbols of quantity’, thereby ‘forming the scattered elements of specious analysis into a system’ – a point Henk Bos recently emphasized when considering that Viète's ‘new algebra was indeed a fully abstract formal system implicitly defined by basic assumptions about magnitudes, dimensions, and scales, and by axioms concerning the operations’.Footnote 41 Chasles went further, however. Intent on tracing out epistemically significant breaks and uncovering stages underlying and punctuating the progress of science, he dug deeper. He investigated what may have laid the groundwork for Viète's innovative step, and therewith offered a paragon example of his deconstructive approach to historiography.
Hallam's emphasis on such ‘scattered material elements of specious analysis’ presumably prefiguring Viète's system was inspired by the late eighteenth-century scholar Pietro Cossali, whose subtle views Chasles partly appropriated and partly overturned. Cossali claimed that Cardano had anticipated Viète, as the so-called regula modi of his Ars magna (1545) assumedly attested.Footnote 42 Cossali referred to Cardano's suggestion that one could solve problems amounting to two linear equations in two unknowns by excerpting a sequence of computations from the reasoning with the unknowns. This sequence could be carried out upon the numerical data of the problem at hand only, and thereby would turn out briefer than the whole reasoning would have been. Cardano's problem would be clothed in an example about the cost of various combinations of green and black silk counted in feet (Figure 2).
Figure 2. Girolamo Cardano, Artis magnae sive regulis algebraicis liber unus (1545), Chapter 29, ‘De regula modi’.
In Cossali's reading, Cardano's rule was obtained from the usual way to solve a problem of the form
$$7x + 3y = 72$$
$$2x + 4y = 52$$by focusing on the sequence of computations operated upon the numerical data alone, and hence by excerpting a formula of the type
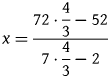$$x = \displaystyle{{72\cdot\displaystyle{4 \over 3}-52} \over {7\cdot\displaystyle{4 \over 3}-2}}$$viz. here, for instance, the formula giving the price of the green silk. With Cardano, Cossali pointed out, the way the numerical data were combined yielded a general rule for all similar questions. One could keep track of the whole sequence of operations and apply it to any other set of numerical data, so that, to a certain extent, the operations themselves were held distinct from the numerical data upon which they were performed. This was presumably in the spirit of Viète, Cossali claimed, although there was still no general expression for such sequences of operations as would later be the case with a proper algebraic formula. Chasles endorsed Cossali's notion that the ‘material elements’ of algebra pre-existed Viète's algebraic symbolism, albeit in piecemeal form, and definitely not where Cossali saw them. Cardano only dealt with numerical data, however astutely. He thus failed to use letters for known quantities; hence, in Chasles's view, he did not belong to Viète's stage, for want of a proper notation for undetermined coefficients.
This archeological gaze was part of Chasles's deconstructive approach. Guided by a now clear grasp of what a complete algebraic symbolism should be, he proceeded in a regressive way and extensively sought any traces or notational rudiments of symbolic algebra in all the extant sixteenth- and fifteenth-century algebraic treatises accessible to him. Key to his attempt at what may be labelled a ‘material’ history of algebra was his acute sense that the bits and pieces of notational technologies he was seeking were to be assessed as both the support and the vehicle of operational agency. In this perspective, notations were not to be separated from the operations of which in return they would prove to be the adequate bearers.Footnote 43 Chasles's whole undertaking was only possible owing to the wealth of first printed editions of ancient algebraic treatises he had acquired over the years and collected in his own personal library by compulsively visiting Parisian bookshops and antiquarians.Footnote 44
Chasles thus highlighted three sixteenth-century algebraists, Michael Stifel (1487–1567), Jacques Peletier du Mans (1517–82), and Jean Butéon, also known as Jean Borrel (1492–1572), for having represented the unknowns by letters, and their powers by means of specific signs which they called exponents. In his Arithmetica integra (1544), Stifel introduced the so-called cossic symbols for the powers of the unknowns, whose exponents were whole numbers, and hence stipulated that the multiplication and division operated upon these symbols were ruled by the addition and the subtraction of their respective exponents. In the case of two unknowns, the powers of the first would be represented by means of the cossic symbols alone, while those of the second unknown would require a second letter A, as for instance 1A 
for the second power of A, viz. A 2; 1A
for A 4; 1Aß for A 5; etc. Chasles deemed these notations an uncontroversial advance with respect to the Italian algebraists who continued to use words and locutions (cosa, censo, cubo, censo di censo, etc.) for the powers of the unknown. Still, he was interested in tracing back to its very source the notational technique contributed by the cossic algebraists. He remarked that Stifel often quoted the works of Christoph Rudolff (1499–1543) and Adam Ries (1492–1559), which oriented his search in this direction. He thus roamed the Bibliothèque royale and exhumed a manuscript copy made in Rome in 1540 of Rudolff's Arithmetica (1522), in which one could plainly see that not only +, −, and 
were used, but also the same symbols for the powers of the unknowns as Stifel's (Figure 3).
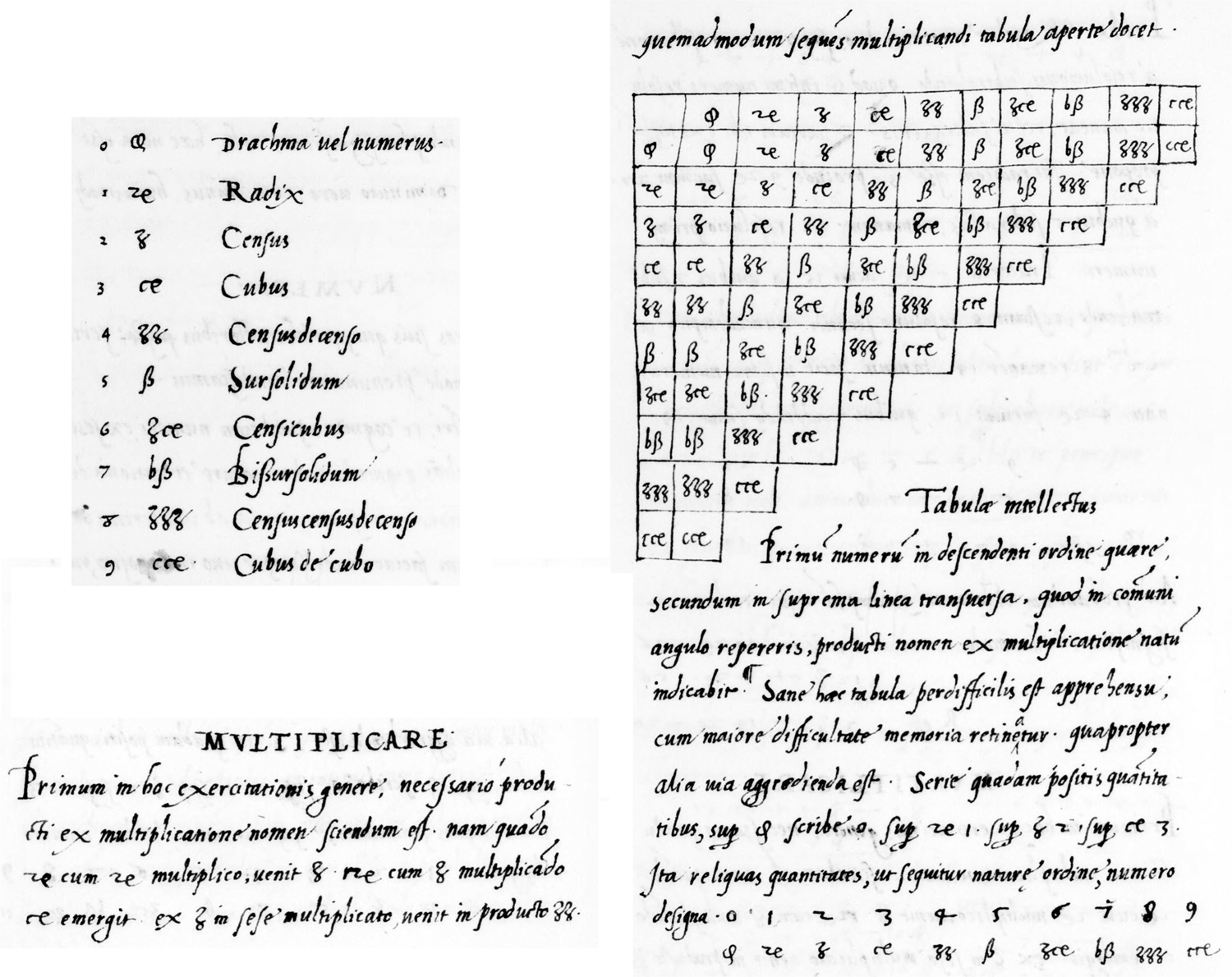
Figure 3. Chistoph Rudolff, Arithmetica (1522), BNF, Ms No. 7365, ff. 32v, 36r, 36v.
Chasles's quest, however, did not stop there. A further track would even lead back to earlier sources for the symbolization of exponentiation. Having remarked that both Jean Butéon and Guillaume Gosselin mentioned a book titled Larismethique by Estienne de la Roche, and first published in 1520, Chasles chased it and got it.Footnote 45 Hence he perused it in order to find evidence for what Butéon and Gosselin had hinted at, namely that it contained a prefiguration of the Cartesian exponential notation. Although underscoring that de la Roche's was heretofore the oldest known algebraic treatise printed in France and written in French, Chasles nevertheless did not fail to notice on folio 42 the reference to a presumably antecedent treatise by Nicolas Chuquet (Figure 4).
Figure 4. Estienne de la Roche, Larismethique novellement composée par maistre Estienne de la Roche dict Villefranche, natif de Lyon (1520), Lyon: Constantin Fradin, f. 42r.
Wondering whether the exponential notation might have been present even earlier than 1520, Chasles hoped that this latter unknown treatise would not be entirely lost. The answer came belatedly. The French scholar Aristide Marre, both a linguist and an orientalist who was also interested in the history of mathematics, found a manuscript at the Bibliothèque nationale, identified as MS 1346, which was none other than the one that Chasles had hoped for. In 1880, the year of Chasles's death, Marre edited the Triparty en la science des nombres by Nicolas Chuquet in Boncompagni's historical journal.Footnote 46 Chasles's thoughtful and productive commitment to archival practices would thus bear fruit by the next generation's standards for a more disciplinary history of mathematics. Still, by the end of the 1840s, his hunch had been confirmed. The book he had spotted had been written in 1484, so Viète's stage had been initiated long before the Italian algebraists.
Through the dispute with Libri, a new subject matter for historical scrutiny had appeared to Chasles: notations, and the operations they support. In return, this material history of algebra would provide grist for another mill. Reading and comparing ancient algebraic treatises not only led to reframing periodization; it also offered insights to create new expressive means for modern geometry. Identifying the use of letters for known quantities as the essential feature of Viète's logistica, Chasles sought to supply geometry with resources equivalent to those algebra ever since boasted and launched into shaping a new notational technology for modern geometry allowing circulations from algebra to geometry.
Geometry made abstract
Whilst he was fending off Libri's arguments at the Académie in Paris, Chasles was also distracted from his peaceful retreat in Chartres by teaching duties at the École polytechnique which he only reluctantly accepted. After the death of Félix Savary in 1841, Chasles was put in charge of the cours des machines, a subject about which he was, as he confessed, largely ignorant.Footnote 47 Chasles's move to Paris and to loftier institutional spheres was further accelerated in the second half of the 1840s. In 1846, a chair of ‘higher geometry’ (géométrie supérieure) was created specifically for Chasles at the Faculté de Paris, in part due to the lobbying of Poinsot, his constant ally in the defence of pure geometry against analysis. Five years later, Libri, already weakened in his institutional seating after a disastrous polemic in public with Liouville in 1843, was found to have stolen and mutilated manuscripts from the libraries he had been tasked to catalogue.Footnote 48 His vacant seat at the Académie was immediately given to Chasles.
The modalities of the production and circulation of Chasles's geometry changed radically after his rise within Parisian academic circles. At the Sorbonne, Chasles found himself in possession of a podium from which he could teach with a great degree of freedom. Not only was he able to teach pure geometry; he could do so whilst weaving into his courses the historiographical and epistemological reflections he had made into an essential part of his research practice. This transformation of the geographical and institutional locales in which Chasles produced his geometrical theories was not without effect on the latter. As Bruno Belhoste noted, ‘one cannot separate a priori mathematical production from the conditions of its reproduction … Teaching itself, [Belhoste continues,] constitutes one particular modality of the socialization of knowledge, wherein the receiver is in a situation of learning, which implies a didactical adaptation [mise en forme] and the invention of specific activities’.Footnote 49 And indeed, the move from his personal library in Chartres to classrooms and prestigious lecture halls in Paris would make it necessary for Chasles to adapt the modalities of the writing and communicating of his geometry.
In the Aperçu historique, Chasles had delivered an exhaustive diagnosis of the causes of the key weakness of ancient geometrical methods, namely their lack of generality. All pure geometry before Monge, according to Chasles, was ‘bristling with figures’, and this limited drastically the degree of generality to which it could aspire. Working upon a configuration consisting in a circle and a straight line, for instance, one had to distinguish between the cases where the line touches the circle, intersects it, or lies entirely outside it.Footnote 50 Similarly, if various points on a straight line entered a proposition, one had to provide different statements and proofs for the various orderings of these points, or for special cases such as that of coinciding points. That pure geometry tackled questions ‘in a concrete form, on the figure itself’, was for Chasles the result of a lack of ‘general and abstract principles’.Footnote 51 Analytical methods had overcome this epistemic barrier, but only at the cost of geometrical intuitiveness and clarity. In Chasles's 1837 narrative, the very possibility of bringing generality and abstraction into pure geometry had been demonstrated by Monge via his courses on descriptive geometry, and for that reason he was credited as the one ushering the fifth and latest epoch in the development of geometrical methods.
By the mid-1840s, Chasles had renewed his understanding of the reasons behind algebra's sweeping effect on the development of mathematics, by stressing the epistemic importance of the introduction of an equal representation of known and unknown quantities by letters and the development of an art of computing on letters. On 22 December 1846, as he delivered the inaugural discourse from his newly created chair, he reassessed his theses on the development of geometrical methods in light of his new understanding of the history of algebra. One crucial departure he made from his earlier narrative expressed in the Aperçu historique is that, to the name of Monge, he added that of Lazare Carnot. In 1837, Carnot had been merely placed amongst the followers of Monge alongside Dupin and Hachette. By 1846, he had been elevated to an equal footing with Monge as an initiator of the modernization of geometrical methods.Footnote 52 Both savants, however, were credited with different contributions.
Amongst Carnot's achievements, Chasles singled out a new solution to a problem posed by Fermat on the contact of spheres, which until then had required the consideration of ‘fourteen preliminary questions, most of which are only particular cases of the main question’.Footnote 53 By contrast, Carnot's solution took on the question in its most general form directly. A few paragraphs later, Chasles praised Carnot's research into systems of coordinates alternative to Descartes's. By circulating between representations of the same curve, Chasles analysed, Carnot had found a way to circulate between the properties thereof.Footnote 54 Carnot's title of glory throughout all these contributions, for Chasles, was to have ‘spread this way of writing Geometry, which has come to characterize modern Geometry’.Footnote 55 Carnot had not just solved geometrical problems with the appropriate level of generality, Chasles argued; he had opened the way for the writing of abstract geometrical methods without the help of algebra.
In the following years, Chasles wove together these new historiographical and epistemological insights within his geometrical practice. In the 1852 Traité de géométrie supérieure, a book borne out of his lectures at the Sorbonne, Chasles sought to introduce novel methods of proof, characterized by ‘uniformity and range of applications’.Footnote 56 And what made these methods so remarkable, for Chasles, was that ‘they partake of the specific advantages of Analysis’; in particular, they elide ‘differences in relative positions of the various parts of a figure’.Footnote 57 To transfer this epistemic strength of algebraic symbols into geometrical expressions, Chasles crafted a new, Carnot-inspired notational technology: the ‘principle of signs’.
Equations between segments and angles in pure geometry, such as the one associated with Desargues's involution (see above), had only been used to express relations between their numerical values, Chasles analysed. Reproducing within geometry the passage from numerical to literal algebra, Chasles proposed to use symbols such as ab to denote not the length of the segment between two points a and b, but the segment itself, upon which certain operations can be carried out. Most importantly, a segment can be inverted, thereby yielding the segment ba = – ba. In this way, Chasles introduced negative symbols in geometry whilst eschewing the long-lasting debates surrounding their meaning (whether empirical or formal) with which he was very familiar.Footnote 58
To illustrate the import of this notational innovation, Chasles considered four points a, b, c, d on a given straight line, and formed the rectangles ab.cd, ac.db, and ad.bc.Footnote 59 It can always be proven that one of these rectangles is equal to the sum of the other two. However, if one regards the symbols ab, cd etc. as denoting the numerical (positive) values of the lengths of the segments thereby defined, one must distinguish between various cases. If the points a, b, c, d are in this order, then the rectangle abcd is the largest of the three. If d is placed between b and c, however, the largest rectangle of the three is adbc. Not only must one separate between cases to state and prove these clearly related propositions, but the equations that translate them differ on a case-by-case basis: in the two configurations given above, they are respectively:
$$ac.bd = ab.cd + ad.bc, \hbox{ and } ad.bc = ad.dc + ac.bd$$Such equations, for Chasles, are mere ‘concrete and purely numerical relations’; one of which must be added every time a new configuration of the parts of the figure under study is considered.Footnote 60 Just as Fibonacci's use of letters to denote numbers was not enough to constitute proper algebra, denoting numerical values such as lengths or angles by symbols is insufficient to elevate geometrical propositions. Operations on geometrical symbols relying on the principle of signs, however, made possible the writing and manipulation of general and abstract propositions. In this case, Chasles could immediately provide a unified expression for all these separate propositions using this principle, namely
$$ab.cd + ac.db + ad.bc = 0$$This abstract equation, whose terms denote oriented segments, does not depend on any particular ordering of the four points. However, one can always specify said ordering, and the general equation shall then turn into one of the concrete relations above. If, for instance, the points are in the order a, b, c, d, then db is the only negative term in this last equation. Adding the negative sign before this term, and interpreting it as a numerical expression, one immediately obtains the first of the two concrete relations given above. In this sense, the principle of signs allows for the expression of ‘complete propositions’.Footnote 61
Equipped with this seemingly simple notation, Chasles would transform the entire symbolic apparatus through which to express the geometrical configurations he had studied for decades. Relying on his analysis of the material history of algebra, he operated with symbols not only for actually given or unknown points and lines, but also for virtually given ones. With these new symbols, generic equations were matched to certain fundamental configurations. Instead of the concrete relation for Desargues's theorem, which he had so expertly analysed in 1837, Chasles would characterize involutions qua configuration via the following equation:
$$\displaystyle{{am\cdot a^{\prime}m} \over {bm\cdot b^{\prime}m}} = {\rm \lambda }$$wherein m refers to a variable point; λ to a given ratio; a, b to two given points; and a′, b′ to their homologues within the figure.Footnote 62 Breaking with the received Cartesian semiotics of x's and y's opened the door for another form of historical circulation. Couched since early modern times in algebraic garb, Apollonius’ De Sectione Determinata, a classical problem of Greek geometry, could now be expressed via the principle of signs. It thus appeared to be one special case of the involution equation above and could thus be solved both geometrically and generally, its connections with the doctrines of modern geometry being made apparent.Footnote 63
This historically minded rewriting would prove decisive for the shaping of Chasles's geometry of curves. One year after the publication of the Traité, this new notational technology yielded what he would call the ‘geometrical equations’ of conics and cubics.Footnote 64 The epistemic break achieved by Descartes's Géométrie and the application of algebra to the theory of curves had been reached anew, only this time with purely geometrical means.
Conclusion
Chasles's modern geometry was not merely constructed against the backdrop of historical studies; it also illuminated them in return. Just a few years after the publication of the Traité, Chasles put forth a new ‘divination’ of the content of Euclid's lost Porisms: anharmonic ratios and his geometrical equations providing the interpretive key thereof.Footnote 65
In the wake of his death in 1880, however, Chasles's interweaving of the historiographical and the mathematical would soon be undone by a new generation of professors and historians of mathematics. In the introduction of his 1887 book La géométrie grecque, Paul Tannery carefully distanced himself from the towering legacy of Chasles's 1837 Aperçu historique. Whereas Chasles drew from the past methodological and epistemological conclusions for his own mathematical practice, Tannery's historical analyses were geared solely towards making this very past into an object of scientific enquiry per se, i.e. ‘submit[ting] sources to methodical critique and according to the principles applicable in such matters’.Footnote 66 At about same time, Gaston Darboux (who officially took over Chasles's chair at the Sorbonne in 1880) devoted no more than a few pages to a brief historical discussion in his course on geometry. History, for Darboux, was only good for the remembrance of past colleagues, and as a way to introduce students with less hurt into the study of advanced mathematics.Footnote 67
In retrospect, however, the fruitfulness of Chasles's joint pursuit of geometrical knowledge on mathematical and historical terrains should be acknowledged and reassessed. From archival visits, studies in deconstructive historiography and epistemological analyses of past methods and notations, he gathered the materials necessary for the construction of a novel theory of geometrical curves. To borrow the words of an acute observer of contemporary changes in historiographical standards and practices, for all the ‘unwisdom’ one can point to in Chasles's teleological reading and use of the past, it remained, first and foremost, ‘history in the service of [mathematical] life’.Footnote 68
Acknowledgements
Our thanks go to the two anonymous reviewers for their helpful remarks and suggestions, as well as to Trish Hatton and Amanda Rees for their careful and efficient handling of our manuscript. This research project was profoundly enriched by many discussions with Karine Chemla, to whom we are grateful.
Open access
