Article contents
‘A Less Agreeable Matter’: The Disagreeable Case of Newton and Achromatic Refraction
Published online by Cambridge University Press: 05 January 2009
Extract
There is no evidence to suggest that even as late as January 1672, when Newton was elected a Fellow of the Royal Society, anyone (except those unknown few who had in the previous years attended his Lucasian lectures at Cambridge) had any inkling of his new theory of colours. His name exploded on the scientific scene as the inventor and constructor of a new kind of telescope—what later became known as the reflector (which was somewhat misleading compared with its name during the seventeenth century: the catadioptrical telescope). Had the erudition of the London virtuosi been a little broader, they would have known that in fact he was not the inventor of the telescope, even though the precise form he gave it was his. Not only was the idea a hundred years old, during which period it was repeatedly suggested by various writers, but also Newton himself took the idea straight from the most recent of these suggestions, namely that included in James Gregory's Optica promota of 1663. The situation becomes even more ironic when we realize that the new instrument was admired for wrong reasons and on merits that were far from Newton's intentions. Nevertheless, admired it was, and there was a good reason for this: Newton's instrument was in fact the first reflector actually to be constructed and, moreover, for a few weeks (before its mirror became tarnished) it performed quite well. Several astonomers became interested because of the high magnifying power relative to its dimensions (about 7 inches long, with a magnification of 38).
- Type
- Research Article
- Information
- Copyright
- Copyright © British Society for the History of Science 1975
References
1 Newton was proposed for membership by Ward, Seth on 21 12 1671Google Scholar. See Birch, T., A history of the Royal Society of London (4 vols., London, 1756–1757), iii. 3Google Scholar; also The correspondence of Isaac Newton, ed. Turnbull, H. W. (Cambridge, 1959-in progress), i. 73Google Scholar: Oldenburg, to Newton, , 2 01 1672Google Scholar, notifying him also of the efforts made in the Royal Society to secure him the priority of the invention by drawing up a description of it and by sending ‘a Solemne letter to Paris to M. Hugens, thereby to prevent the arrogation of … strangers’. Newton, with some show of warmth, wrote back: ‘I am very sensible of the honour done me … in proposing me candidate & which I hope will bee further conferred upon mee by my Election into the Society’ (ibid., p. 80). Five days later he was elected.
2 Newton, erudite scholar that he already was, was acquainted with Gregory's book well before he started building his own instrument:
‘For when I first applyed my selfe to try the effects of reflections, MrGregory, 's Optica Promota (printed in ye yeare 1663)Google Scholar being fallen into my hands, where there is an instrument described (pag. 94) … I had thence an occasion of considering that sort of constructions, & found their disadvantages so great yt I saw it necessary before I attempted any thing in Practique to alter the design of them’; Newton, to Oldenburg, , 4 05 1672Google Scholar, in Correspondence of Newton, op. cit. (1), i. 153.Google Scholar
See also the earliest evidence of Newton's actual construction of the telescope in his letter of 23 February 1669, where he refers to his having ‘promoted optics’ by the new instrument, an expression which may be plausibly interpreted as an echo of Gregory's Optica promota.
3 On first being informed of Newton's instrument by Collins, Flamsteed wrote back urgently asking for its specifications. He was particularly excited by the possibilities for observational astronomy implied by this ‘short telescope … made to perform as much as a long one, which you say that Mr Newton has not only proved by demonstration but [by] fact’; see Rigaud, S. J. (ed.), Correspondence of scientific men of the 17th century (2 vols., London, 1841), ii. 93Google Scholar. Oldenburg's preliminary annoucement of the new instrument to Huygens on 1 January 1672 concentrated on its having a focal length of only 6 inches but a magnifying power nine times greater than a normal refractor of 25 inches focal length; see Correspondence of Newton, op. cit. (1), 1. 72Google Scholar. The formal account later sent to him in the Philosophical transactions of the Royal Society, vii (1672), 4004Google Scholar (see Correspondence of Newton, op. cit. [i], i. 74–6Google Scholar) is similarly worded. Huygens, in his answer, is similarly impressed by the ingenuity of the idea of using a concave mirror to contract the telescope's length while increasing its magnification relative to a standard refractor (ibid., i. 90). Flamsteed wrote to Collins again on 31 January 1672, after Newton's reflector had been submitted to the Royal Society, asking once more for the specifications of ‘this prodigy of art’ and venturing a guess that it ‘cannot augment ye representation so extraordinarily as is related’ by mere reflections but must presumably employ a concave mirror (ibid., i. 88). And again, on 17 April, he implored Collins to inform him ‘at what rates they [Newton's reflectors made by Cox] are valued and with what effect they perform. I mean how I may buy one of about 2½ feet and whether it will be as well as a long one of 30 feet’ (ibid., i. 146).
4 Correspondence of Newton, op. cit. (1), i. 83.Google Scholar
5 Ibid., i. 92–102. For its published form, see Philosophical transactions, vi (1671–1672), 3075–87.Google Scholar
6 Correspondence of Newton, op. cit. (1), i. 95.Google Scholar
7 As usual, this was declared only in the published papers, but the detailed mathematical theorems proving it had already been expounded in Newton's Lectiones opticae. The February paper was in fact only a popular article. Newton probably felt that in it he should not enter into any mathematical detail, since he was then preparing for publication the Lectiones, where it would be given in full. The failure to include a rigorous mathematical framework in this unfortunate paper was the principal cause of the ensuing disputes over its content and purpose, which in turn, by a cruel twist, led Newton to abandon his intention of publishing the Lectiones.
8 On the background of Oldenburg's suppression of certain paragraphs in Newton's first paper and later answer, see Cohen, I. B., ‘Versions of Isaac Newton's first published paper’, Archives internationales d'histoire des sciences, xi (1958), 357–75Google Scholar. I have developed this in Bechler, Z., ‘Newton's disputes of 1672: a study in the grammar of dissent in science’, in Elkana, Y. (ed.), Chapters in the interaction between science and philosophy (New York: Humanities Press, 1974), pp. 115–42Google Scholar; I argue there that the main theme of the optical dispute of 1672—with Hooke, Pardies, and Huygens—was, in fact, this disputed claim to necessity. Newton thereby broke the contemporary rules of sane and scientific style. See also Bechler, Z., ‘Newton's efforts to reduce his optics to mechanics—the failure of one philosophy of scientific procedure’ (Hebrew University of Jerusalem Ph.D. thesis, 1972)Google Scholar, where the reaction to this revolutionary style is set in the general context of the scientific problems of the early 1670s.
9 On 23 February 1672 Collins sent Gregory a letter containing a transcript of Newton's earliest mention of his new telescope; see Newton, 's letter to Collins, , 23 02 1669Google Scholar, in Correspondence of Newton, op. cit. (1), i. 3Google Scholar, and Collins's comments thereon. Collins first quoted Hooke's note in the Record Book from memory, then later verified it and transcribed the actual version—the one I have quoted—in his covering letter; see Turnbull, H. W. (ed.), James Gregory tercentenary memorial volume (London, 1939), p. 29Google Scholar. Gregory, who was the only scientist we know actually to have undertaken the polishing of a reflector (the attempt failed for lack of an adequate reflecting material and through a failure to realize the adequacy of spherical surfaces for the purpose), remained silent for a long time; see King, H. C., The history of the telescope (London, 1955), pp. 71–2.Google Scholar
10 Philosophical transactions, i (1665–1666). 67.Google Scholar
11 Ibid., p. 203.
12 ‘I provided me a Tube of Brass, … into the smaller end of this I fixt with Wax a good piano convex Object Glass, with the convex side towards the Object, and into the bigger end I fixt also with Wax a pretty large plano convex Glass, with the convex side towards my eye, then by means of the small hole by the side, I filled the intermediate space between these glasses with very clear Water, and with a screw stopp'd it in; then putting on a Cell for the Eye, I could perceive an Object more bright then I could when the intermediate space was only fill'd with Air, but this, for other inconveniences, I made but little use of.’; Hooke, R., Micrographia (London, 1665), Preface, p. 11.Google Scholar
13 The London plague of 1665 played its role in determining the course of the development of English optics. But while it smiled on Newton, it frowned on Hooke who ‘affirmed coram multis that in the year 1664 he made a little Tube of about an Inch long, to put in his fobb, which performs more than any Tellescope of 50 foot long made after the common manner; but the Plague happening wch caused his absence, & the fire whence rebounded profitable employments about the Citty, he neglected to prosecute the same, being unwilling the Glasse grinders should known any thing of the Secret.’; see Gollins, 's letter to Gregory, , 23 02 1672Google Scholar, in Correspondence of Newton, op. cit. (1), i. 4.Google Scholar
14 Ibid.
15 The essay ‘Of refractions’ was first described by Hall; see Hall, A. R., ‘Sir Isaac Newton's notebook 1661–65’, Cambridge historical journal, ix (1948), 239–50CrossRefGoogle Scholar. The refraction table of f. 33v is reproduced from Collins's inaccurate contemporary copy in Correspondence of Newton, op. cit. (1), i. 103Google Scholar. The texts, together with a detailed mathematical analysis, of the passages on the compound lens and spherical aberration ‘errors’ are now available, reordered into a logical sequence, in Whiteside, D. T. (ed.), The mathematical papers of Sir Isaac Newton (Cambridge, 1967-in progress), i. 572–6Google Scholar. The pages containing them, which were afterwards torn out of the notebook, are now in private possession.
16 Using his derived expressions for the principal focus distance f of a spherical surface of radius r, which separates two media with the relative refractive index n—namely (n-1)/r=1/f—Newton obtains (n/m—1) 1/BF = 1/BE for the simple lens, and (e/d—1) 1/AC = 1/AF for the water-glass interface. Again, using (nα—1) 1/r = 1/fe for the conjugate focus fe, where α is the measure of the inclintion of the incident ray to the main axis, and putting α = DF/BF, r = BD, he obtains for the glass-air interface [(d/f)DF/BF-1] 1/BD = 1/BE. This is equivalent to the better-known expression (n1/q) — (n2/p) = (n1–n2)/R, where q = BE, p = BF, n1 = d, n2 = f.
17 Cambridge University Library (henceforth cited as U.L.C.), Add. 3970, f. 445r (all manuscript quotations hereafter refer to this Add., unless specifically stated otherwise); also in Philosophical transactions, lxxxviii (1672), 116.Google Scholar
18 Ibid.
19 Ibid.
20 See f. 433r.
21 The opening of version A was:
‘Sr, I am much pleased that so ingenious & experienced a person as Mr Hook hath taken my discourse about refractions & colors into consideration, & I desire that my thanks bee returned to him for his observations, & more especially for his confirmation of the experiments.’ (f. 433r).
Newton crossed this out in version B and went on to pen the opening which was finally published, followed by this singularly aggressive sentence, which he crossed out and omitted in all subsequent versions:
‘For the whole discourse consists in ascribing an Hypothesis to me wch is not mine, in asserting an Hypothesis of his own wch as to the principal parts of it is not against me, & in denying some things the truth of which would have soon appeared by prosecuting that method of experiments wch I insinuated.’ (f. 447r).
The next sentence he did not cross out, but he omitted it from subsequent versions as well: ‘Yet I must confess that at the first reading of those considerations I was a little troubled to find a person so much concerned for an Hypothesis from whom in particular I most expected an unconcerned & indifferent examination of wt I proposed.
22 Ibid.
23 f. 445r.
24 f. 433r.
25 Ibid.
26 Ibid.
27 See Hooke, , op. cit. (12), pp. 58–9.Google Scholar
28 f. 443r.
29 Ibid.
30 Ibid.
31 ff. 443r - 444r.
32 Put I1, I2, R1, and R2 for the angles of incidence and refraction of the extreme ‘blue’ and ‘red’ rays at the glass-water interface, and i1, i2, r1; and r2 as the corresponding angles of the water-air interface, so that n1 = sin r1/sin i1, n2 = sin r2/sin i2, N1 = sin R1/sin I1, N2 = sin R1/sin I2; then, given that I1 = I2 = I (since the incident ray is white), the condition for achromaticity in this compound prism will be r1 = r2 = r. It follows that n1/n2 = sin i1/i2 and N1/N2 = sin R1/R2. Since i1 + R1= i2+R2 = 180 — a (where a is the angle of inclination of the glasswater and air-water interfaces), the parallelism of the emerging ray to the incident ray will require I + r = i1 + R1 = 180 — a. Hence a necessary condition for an emerging (non-parallel) refracted ray to be white will be I + r < 180 — α.
33 Whiteside, , op. cit. (15), iii. 526–9.Google Scholar
34 Ibid. iii, 527. In Figure 3 let X be the mirror's centre, so that ![]() Pdx =
Pdx = ![]() QdX and (by the second condition)
QdX and (by the second condition) ![]() SdX =
SdX = ![]() RdX, whence
RdX, whence ![]() QdR =
QdR = ![]() PdS, or, as Newton puts it, ‘the image's angular translation from Q to R will be as much as it is from P to S.’
Now, the first condition is expressed by
PdS, or, as Newton puts it, ‘the image's angular translation from Q to R will be as much as it is from P to S.’
Now, the first condition is expressed by
![]() where n is the refractive index of the mirror's glass coating, and R1, R2 its two radii. The second condition is expressed by 1/ES + 1/ER = 2/R2, while the refraction of the parallel ray at the primary lens gives 1/BO = (n — 1) (1/r1 + 1/r2), where r1, r2 are the radii of its convex faces, and its refractive index is assumed to be the same as that of the mirror's glass coating. Substituting (n — 1) gives
where n is the refractive index of the mirror's glass coating, and R1, R2 its two radii. The second condition is expressed by 1/ES + 1/ER = 2/R2, while the refraction of the parallel ray at the primary lens gives 1/BO = (n — 1) (1/r1 + 1/r2), where r1, r2 are the radii of its convex faces, and its refractive index is assumed to be the same as that of the mirror's glass coating. Substituting (n — 1) gives
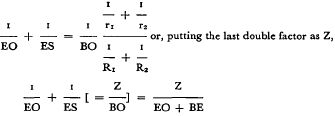
35 f. 445r.
36 f. 447v.
37 Whiteside, , op. cit. (15), iii. 511–13.Google Scholar
38 Newton, I., Principia, translated by Motte, A., revised by Cajori, F. (Berkeley: University of California Press, 1962), p. 233.Google Scholar
39 Newton, I., Opticks (London, 1704), p. 74.Google Scholar
40 Ibid.
41 Ibid., p. 94.
42 The following may be a plausible suggestion: As has been shown, the relation, which could well have been known to Newton, giving the principal focal length f of a compound twomedia lens, is (n1 — 1) K — (n2 — 1) L = 1/f (where K and L are expressions in the lenses' radii). Hence, for f = ∞, which means that the emerging rays are unrefracted, or parallel to the axis, we obtain (n1 — 1)/(n2 — 1) = K/L. On the other hand, the condition for the achromaticity of this lens is dn1/dn2 = K/L; and I have earlier suggested that this relation could well have been known to Newton at least since his ‘Delineatio’. Now, experiment 8 posits that such achromaticity implies an infinite focus, and hence there follows dn1/dn2 = (n1 — 1)/ (n2 — 1).
The second route that could indicate Newton's source for his dispersion theorem is to compute the expression for the deviation of a ray after refraction in a compound prism of the sort described in his earlier experiment 9 and the present experiment 8. The deviation angle of the emerging ray relatively to the incident ray is given (for thin prisms of small refracting angles a1, a2, etc., and small angles of incidence, corresponding to the thin lenses and the rays parallel to the axis in the above expression for compound lenses) by
Δ = (n1 — 1) a1 — (n2 — 1) a2 + (n3 — 1) a3 —…
Since, in experiment 8, n1 = n3, the condition for zero refraction, namely
Δ = o, gives (n1 — 1)/(n2 — 1) = a2/(a1 + a3), while the condition for achromaticity, namely
(n1R —1) (a1 + a3) — (n2n — 1) a2 = (n1B — 1) (a1 + a3) — (n2B — 1) a2, gives
(n1a — n1B)/(n2B — n2B) = dn1/dn2 = a2/(a1 + a3). If these two conditions are equivalent, as experiment 8 claims, then the relationship dn1/dn2 = (n2—1)/(n2—1) follows at once.
43 Newton, , op. cit. (39), p. 96.Google Scholar
44 Priestley, J., The history and present state of discoveries relating to vision, light and colours (London, 1772), p. 475.Google Scholar
- 16
- Cited by


