3.1. Classes of Stakeholders

Figure 1 shows the participants in the longevity risk transfer market. In this section, we examine the various classes of stakeholders in this market.

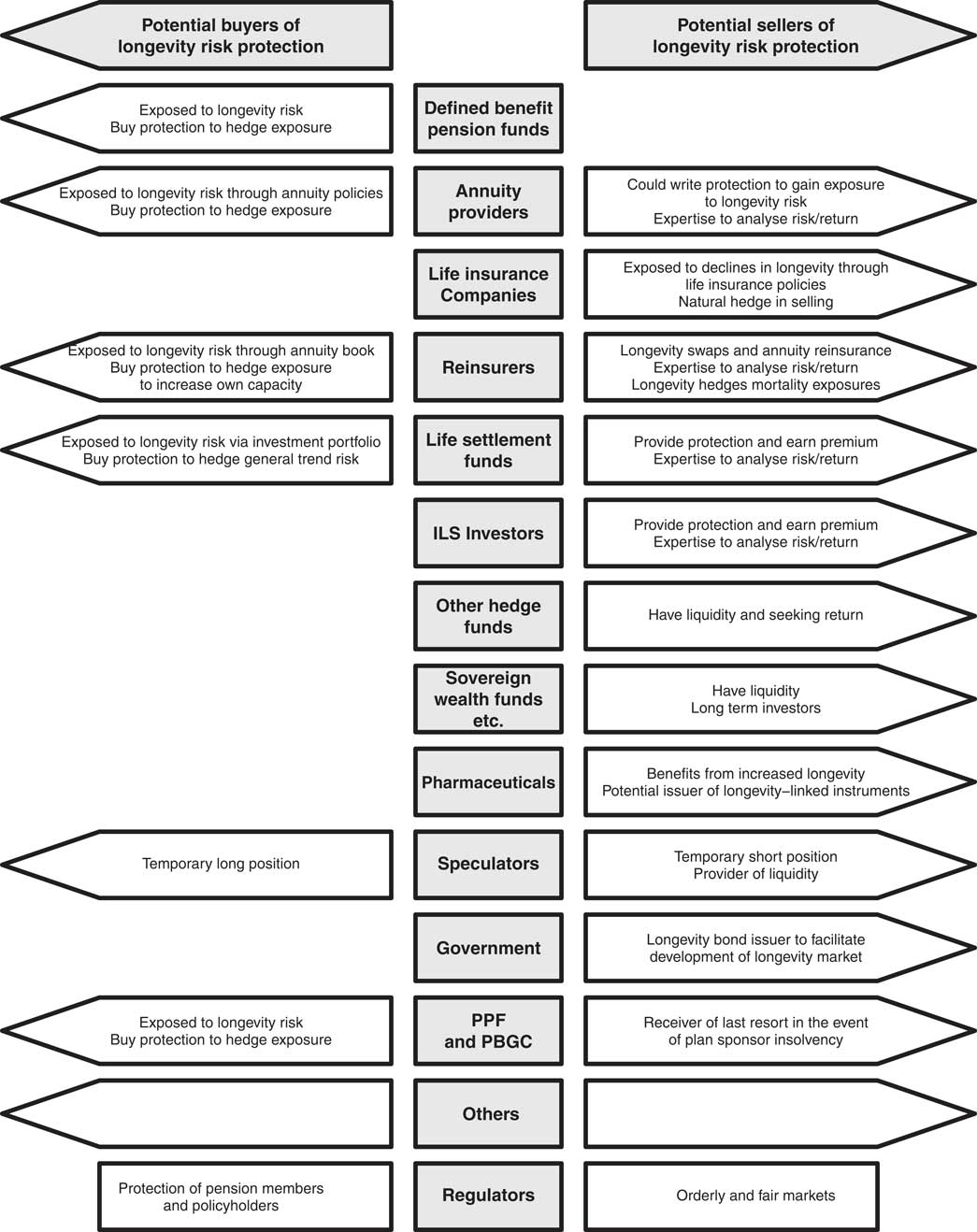
Figure 1 Participants in the Longevity Risk Transfer Market

Source: Adapted from Loeys et al. (Reference Loeys, Panigirtzoglou and Ribeiro2007, Chart 10); PPF, Pension Protection Fund, PBGC, Pension Benefit Guaranty Corporation.

3.2. Hedgers

3.2.1. One natural class of stakeholders are hedgers, those who have a particular exposure to longevity risk and wish to lay off that risk. For example, defined benefit (DB) pension funds and annuity providers stand to lose if mortality improves by more than anticipated, while life insurance companies stand to gain, and vice versa. These offsetting exposures imply that annuity providers and life assurers, for example, can hedge each other’s longevity risks.Footnote ¹¹ Alternatively, parties with unwanted exposure to longevity risk might pay other parties to lay off some of their risk. For instance, a life office might hedge its longevity risk using a reinsurer or by selling it to capital market institutions.

3.2.2. As another possibility, pharmaceutical companies benefit if people live longer, since they (and the health service) need to spend more on medicines as they get older, especially for those in poor health. Also there is a continuous stream of new medical treatments that prolong life. The pharmaceutical companies could potentially issue longevity-linked debt to finance their research and development programmes which, if sufficiently attractive for pension funds to hold, could be issued at a lower cost than conventional fixed maturity debt. In other words, pharmaceutical companies benefit if longevity increases and could put on a counterbalancing position by issuing longevity bonds.Footnote ¹² While they have been approached about this possibility, no pharmaceutical company has yet issued such debt. The principal reasons appear to be that the finance directors have not been made sufficiently aware of the potential benefits of such an issue – and in any case are more concerned that the millions of dollars being spent on drug trials will bring a sufficient return to shareholders – and because, in practice, the short-term correlation between company profits and longevity is probably not strong enough to persuade finance directors to issue longevity bonds.

3.3. Specialist and General Investors

There are specialist investors in this market, such as life settlementFootnote ¹³ investors, premium finance investors,Footnote ¹⁴ and insurance-linked securities (ILS) investors.Footnote ¹⁵ Depending on their existing exposures, these investors could either buy longevity protection or sell it and earn a premium. General investors include short-term investors, such as hedge funds and private equity investors and long-term investors, such as sovereign wealth funds, endowments and family offices. Provided expected returns are acceptable, such investors might be interested in acquiring an exposure to longevity risk, since it has a low correlation with standard financial market risk factors. The combination of a low beta and a potentially positive alpha should therefore make mortality-linked securities attractive investments in diversified portfolios.

3.4. Speculators and Arbitrageurs

A market in longevity-linked securities might attract speculators: short-term investors who trade their views on the direction of individual security price movements. The active involvement of speculators is important for creating market liquidity as a by-product of their trading activities, and is in fact essential to the success of traded futures and options markets. However, liquidity also depends on the frequency with which new information about the market materialises and this is currently sufficiently low that there is negligible speculator interest in the longevity market at the present time. Arbitrageurs seek to profit from any pricing anomalies in related securities. For arbitrage to be a successful activity, it is essential that there are well-established pricing relationships between the related securities: periodically, prices get out of line which creates profit opportunities which arbitrageurs exploit.Footnote ¹⁶ However, the longevity market is currently not sufficiently well developed for arbitrage opportunities to exist.

3.5. Governments

3.5.1. Governments have many potential reasons to be interested in markets for longevity-linked securities. They might wish to promote such markets and assist financial institutions that are exposed to longevity risk (e.g. they might issue longevity bonds that can be used as instruments to hedge longevity risk).Footnote ¹⁷

3.5.2. Governments might also be interested in managing their own exposure to longevity risk. They are a significant holder of this risk in their own right via pay-as-you-go state pensions, pensions to former public sector employees and their obligations to provide health care for the elderly. At a higher level, governments are affected by numerous other economic factors, some of which partially offset their own exposure to longevity risk (for example income tax on private pensions continues to be paid as people live longer).

3.6. Regulators

3.6.1. Financial regulators have two main stated aims: (i) the enhancement of financial stability through the promotion of efficient, orderly and fair markets and (ii) ensuring that retail customers get a fair deal.Footnote ¹⁸ The two financial regulators in the UK responsible for delivering on these aims are the Prudential Regulatory Authority (PRA) and the Financial Conduct Authority (FCA).

3.6.2. The PRA has a duty to ensure that the financial system is protected against systemic risks and longevity risk is a potential example of such a risk. This, in turn, requires that carriers of such risks, such as life insurance companies, issue sufficient regulatory capital to protect themselves from insolvency with a high degree of probability. The FCA’s duty is to ensure that customers get competitive and fairly priced annuity products, for example, and that becomes more difficult if providers of these products cannot easily or economically hedge the longevity risk contained in them.Footnote ¹⁹

3.6.3. Another interested regulator is The Pensions Regulator (TPR) which acts as gatekeeper to the UK’s pension lifeboat, the Pension Protection Fund (PPF).Footnote ²⁰ TPR wants to reduce the probability that large companies (in particular) are bankrupted by their pension funds (Harrison & Blake, Reference Harrison and Blake2016). As “insurer of last resort,” the Government is also potentially the residual holder of this risk in the event of default by the PPF. The PPF and Government have a strong incentive to help companies hedge their exposure to longevity risk, which would reduce the likelihood of claims on the PPF. The PPF faces the systematic risk that longevity projections go up generally for plans (without diversifying away between plans), which (i) pushes some plans into the PPF and (ii) increases existing PPF liabilities.Footnote ²¹

3.7. Other Stakeholders

Other domestic stakeholders include healthcare providers and insurers, providers of equity release (or reverse or lifetime) mortgages and securities managers and organised exchanges, all of which would benefit from a new source of fee income. Members of both DB and defined contribution (DC) plans have an interest in protecting their current and future pension entitlements, although the risks in the two types of plan are different. In the case of DB, the security of the plan itself is at stake, with the member facing the risk of lower (e.g. PPF) benefits if the plan sponsor becomes insolvent. In the case of DC, the member is exposed either to the vagaries of the individual annuities market or to the risk of drawing down benefits too quickly and surviving longer than expected. Finally, individuals with state pensions are ultimately not immune from increases in the government’s budget deficit that arise from increases in life expectancy: (i) state pensions could fall (in real terms) for current pensioners, (ii) the state pension age could increase even further than currently planned for future pensioners and (iii) all current and future generations of tax payers are ultimately liable for the increased cost. Longevity risk is a global phenomenon, so there will be similar stakeholders in other countries where this problem is prevalent.

4.1. Overview

The traditional solution for dealing with unwanted longevity risk in a DB pension plan or an annuity book is to sell the liability via an insurance or reinsurance contract. This is known as a pension buy-out (or pension termination) or, in an insurance context, a group/bulk annuity transfer. More recently, pension buy-ins and longevity insurance (the insurance term for a longevity swap) have been added to the list of insurance-based solutions for transferring longevity risk. Insurance solutions are generally classified as “customised indemnification solutions,” since the insurer fully indemnifies the hedger against its specific risk exposure. These solutions can also be thought of as “at-the-money” hedges, since the hedge provider is responsible for any increase in the liability above the current best estimate assumption on a pound-for-pound basis.

4.2. Pension Buy-outs

4.2.1. The most common traditional solution for DB pension plans is a full pension buy-out, implemented by a regulated life assurer. The procedure can be illustrated using the following simple example.

4.2.2. Consider Company ABC with pension plan assets (A) of 85 and pension plan liabilities (L) of 100, valued on an “ongoing basis”Footnote ²² by the plan actuary; this implies a deficit of 15. ABC approaches life assurer XYZ to effect a pension buy-out. On a full “buy-out basis,” the insurer values the pension liabilities at 120, a premium of 20 to the plan actuary’s valuation, implying a buy-out deficit of 35. The insurer, subject to due diligence, offers to take on both the plan assets A and plan liabilities L provided the company contributes 35 from its own resources (or from borrowing) to cover the buy-out deficit. Following the acquisition, the insurer implements an asset transition plan which involves exchanging certain assets, e.g. cash or equities for bonds or loans, and implementing interest rate and inflation swaps to hedge the interest-rate and inflation risk associated with the pension liabilities.Footnote ²³

4.2.3. The advantages to the company are that the pension liabilities are completely removed from its balance sheet. In the case where the company does not have the cash resources to pay the full cost of the buy-out, the pension deficit (on a buy-out basis) is often replaced by a loan which, unlike fluctuating pension liabilities, is an obligation that is readily understood by investment analysts and shareholders. The company avoids volatility in its profit and loss account coming from the pension plan,Footnote ²⁴ the payment of levies to the PPF, administration fees on the plan and the potential drag on its enterprise value arising from the pension plan. The advantage of a buy-out to the pension trustees and plan members is that pensions are now secured in full (subject to the credit risk of the life assurer).

4.2.4. There is a potential disadvantage in terms of timing. Once a buy-out has taken place, it cannot generally be renegotiated if circumstances change and the buy-out price is lower in the future, say, because an increase in long-term interest rates leads to the discount rate used to value pension liabilities also increasing. There is also a potential risk that the buy-out company itself becomes insolvent in which case the pensioners would have no recourse to the PPF. However, since buy-out companies are established as insurance companies with solvency capital requirements,Footnote ²⁵ this risk should, in practice, be very low in countries like the UK.

4.3. Pension Buy-ins

4.3.1. Buy-ins are insurance transactions that involve the bulk purchase of annuities by the pension plan to hedge the risks associated with a subset of the plan’s liabilities, typically associated with retired members. The annuities become an asset of the plan and cover the specific mortality characteristics of the plan’s membership in terms of age, gender and pension amount – but the individual members do not receive annuity certificates.

4.3.2. Buy-ins are often part of the journey to a full buy-out. They can be thought of as providing a “de-risking” of the pension plan in economic terms. If purchased in phases, they enable the plan to smooth out annuity rates over time and avoid a spike in pricing at the time it decides to proceed directly to a full buy-out. Buy-ins also offer the sponsor the advantage of full immunisation of a portion of the pension liabilities for a lower up-front cash payment relative to a full buy-out – although the recent introduction of deferred premium payments for both buy-ins and buy-outs has helped to spread costs for both types of product.Footnote ²⁶

4.3.3. Since the annuity contract purchased in a buy-in is an asset of the pension plan, rather than an asset of the plan member, the pension liability remains on the balance sheet of the sponsor. Plan members are therefore still exposed to the risk of sponsor insolvency if the plan is in deficit and (indirectly) to the risk of insurance company insolvency unless the buy-in deal has been fully collateralised.

4.4. Longevity Insurance or Insurance-Based Longevity Swaps

4.4.1. The third successful solution is the longevity insurance contract or insurance-based longevity swap. This is effectively an insurance version of the capital-markets-based longevity swap (discussed in the next section), which transfers longevity risk only.Footnote ²⁷ A typical structure involves the buyer of the swap paying a pre-agreed fixed set of cash flows to the swap provider and receiving in exchange a floating set of cash flows linked to the realised mortality experience of the swap buyer, the latter being used to pay the pensions for which the swap buyer is liable. No assets are transferred and the pension plan typically retains the investment risks associated with the asset portfolio. Longevity swaps have the advantage that they remove longevity risk without the need for an upfront payment by the sponsor and allow the pension plan trustees to retain control of the asset allocation.

4.4.2. The first publicly announced longevity swap took place in April 2007 between Swiss Re and Friends’ Provident, a UK life insurer. It was a pure longevity risk transfer and was not tied to another financial instrument or transaction. The swap was based on Friends’ Provident’s £1.7bn book of 78,000 pension annuity contracts written between July 2001 and December 2006. Friends’ Provident retains administration of policies. Swiss Re makes payments and assumes longevity risk in exchange for an undisclosed premium.

4.4.3. In any longevity swap, the hedger of longevity risk (e.g. a pension plan or insurer) receives from the longevity swap provider the actual paymentsFootnote ²⁸ it must pay to pensioners and, in return, makes a series of fixed payments to the hedge provider.Footnote ²⁹ In this way, if pensioners live longer than expected, the higher pension amounts that the pension plan must pay are offset by the higher payments received from the provider of the longevity swap. The swap therefore provides the pension plan with a long-maturity, customised cash flow hedge of its longevity risk.

4.4.4. Figure 2 shows the set of cash flows in a typical longevity swap involving a pension plan wishing to hedge its longevity risk exposure. The plan makes a set of pre-agreed fixed payments (each payment is based on an amount-weighted survival rate (Dowd et al., Reference Dowd, Blake, Cairns and Dawson2006; Dawson et al., Reference Dawson, Blake, Cairns and Dowd2010)) and receives the actual pension payments it needs to make (these will be based on its realised longevity experience).

Figure 2 A longevity swap involves the regular exchange of actual realised pension cash flows and pre-agreed fixed cash flows

Source: Coughlan (Reference Coughlan2007a).

5.1. Overview

In this section, we analyse the small number of capital market securities that have been successfully launched since 2006: longevity-spread bonds, longevity swaps, q-forwards, S-forwards and tail-risk protection (or longevity bull call spreads). The key feature of these is that most are index rather than customised solutions.Footnote ³⁰

5.2. Longevity-Spread Bonds

5.2.1. In December 2010, Swiss Re issued an 8-year catastrophe-type bond linked to longevity spreads. To do this, it used a special purpose vehicle, Kortis Capital, based in the Cayman Islands.Footnote ³¹ The Kortis bond is designed to hedge Swiss Re’s own exposure to longevity risk.Footnote ³² It had a very small nominal value of just $50 m, which clearly meant that it was designed to test the water for a new type of capital market instrument.

5.2.2. The bond holders received quarterly coupons equal to 3-month LIBOR plus a margin. In exchange, they were exposed to the risk that the difference between the annualised mortality improvement in English & Welsh males aged 75–85 over a period of 8 years and the corresponding improvement in US males aged 55–65 is significantly larger than anticipated. The mortality improvements were measured over 8 years from 1 January 2009 to 31 December 2016. The bonds matured on 15 January 2017,Footnote ³³ although there was an option to extend the maturity to 15 July 2019. The principal was at risk if the Longevity Divergence Index Value (LDIV) exceeded the attachment point or trigger level of 3.4% over the risk period. The exhaustion point, at or above which there would be no return of principal, is 3.9%. The principal would be reduced by the principal reduction factor (PRF) if the LDIV lies between 3.4% and 3.9%.

5.2.3. The LDIV is derived as follows. Let m ^y (x,t) be the male death rate at age x and year t in country y. This is defined as the ratio of deaths to population size for the relevant age and year. Annualised mortality improvements over n years are defined as:

(1) $$Improvement_{n}^{y} \left( {x,t} \right){\equals}1{\minus}\left[ {{{m^{y} \left( {x,t} \right)} \over {m^{y} \left( {x,t{\minus}n} \right)}}} \right]^{{{1 \over n}}} $$

The annualised mortality improvement index for each age group is found by averaging the annualised mortality improvements across ages x ₁ to x ₂ in the group:

(2) $$Index\left( y \right){\equals}{1 \over {1{\plus}x_{2} {\minus}x_{1} }}\mathop{\sum}\limits_{x{\equals}x_{1} }^{x{\equals}x_{2} } {Improvement_{n}^{y} \left( {x,t} \right)} $$

In the case of the Kortis bond, n is equal to 8 years. The LDIV is defined as:

(3) $$LDIV{\equals}Index\left( {y_{2} } \right){\minus}Index\left( {y_{1} } \right)$$

where y ₂ is the England & Wales population aged 75–85 and y ₁ is the US population aged 55–65. The PRF is calculated as follows:

(4) $$PRF{\equals}{{LDIV{\minus}Attachment\,point} \over {Exhaustion\,point{\minus}Attachment\,point}}$$

with a minimum of 0% and a maximum of 100%.

5.2.4. Proceeds from the sale of the bond were deposited in a collateral account at the AAA-rated International Bank for Reconstruction and Development (i.e. the World Bank). If there is a larger-than-expected difference between the mortality improvements of 75–85 year old English & Welsh males and those of 55–65 year old US males, part of the collateral will be sold to make payment to Swiss Re and, as a consequence, the principal of the bond would be reduced. The exposure that Swiss Re wished to hedge comes from two different sources. For example, Swiss Re is the counterparty in a £750 m longevity swap with the Royal County of Berkshire Pension Fund which was executed in 2009, and so is exposed to high-age English & Welsh males living longer than anticipated. It has also reinsured a lot of US life insurance policies and is exposed to middle-aged US males dying sooner than expected. The longevity-spread bond provided a partial hedge for both tail exposures.

5.2.5. Standard & Poor’s rated the bond BB+ which took into account the possibility that investors would not receive the full return of their principal. This rating was determined using two models developed by RMS which was appointed as the calculation agent for the bonds.Footnote ³⁴

5.2.6. Table 1 shows estimated loss probabilities for the bond using the RMS models. Figure 3 presents a fan chart of the projected LDIV showing the 98% confidence interval.

Table 1 Estimated Loss Probabilities for the Swiss Re Longevity-Spread Bond

Note: ⁽¹⁾attachment probability; ⁽²⁾exhaustion probability.

Source: Standard and Poor’s (2010) Presale information: Kortis Capital Ltd. Tech. Report.

Figure 3 Fan chart of the projected LDIV showing the 98% confidence interval

Source: Hunt & Blake (Reference Hunt and Blake2015, Figure 8).

5.2.7. This was the first time that the risk of individuals living longer than expected has been traded in the form of a bond. Investors had been reluctant to hold longevity risk long term, but short-term bonds might make bearing the risk more acceptable. The bond therefore represented a significant breakthrough for capital market solutions. Nevertheless, there appears to have been very little trading in the bond and no further examples of the bond have so far been issued.

5.3. Capital-Markets-Based Longevity Swaps

5.3.1. The first capital-markets-based longevity swap took place in July 2008 between J. P. Morgan and Canada Life in the UK (Trading Risk, 2008). The contract was a 40-year maturity £500 m longevity swap that was linked to the actual mortality experience of the 125,000-plus annuitants in the annuity portfolio that was being hedged. This transaction brought capital markets investors into the longevity market for the very first time, as the longevity risk was passed from Canada Life to J. P. Morgan and then directly on to investors.

5.3.2. This has become the archetypal longevity swap upon which other transactions are based. Insurance companies, such as Rothesay Life, have adapted its structure and collateralisation terms to an insurance format.

5.3.3. It is important to note that the J. P. Morgan – Canada Life swap was a customised swap, since it was linked to the actual mortality experience of the hedger. All insurance-based longevity swaps in the UK have also been customised swaps to date. However, such swaps are harder to priceFootnote ³⁵ and are potentially more illiquid than index-based swaps which are based on the mortality experience of a reference population, such as the national population. Most longevity swaps sold into the capital markets are index-based. These issues are discussed in more detail in section 8.

5.4. q-Forwards (or Mortality Forwards) and S-Forwards (or Survivor Forwards)

5.4.1. A mortality forward rate contract is referred to as a “q-forward” because the letter “q” is the standard actuarial symbol for a mortality rate. It is the simplest type of instrument for hedging longevity (and mortality) risk (Coughlan et al., Reference Coughlan, Epstein, Sinha and Honig2007b).Footnote ^{36 ,} Footnote ³⁷

5.4.2. The first capital markets transaction involving a q-forward took place in January 2008. The hedger was buy-out company Lucida (Lucida, 2008; Symmons, Reference Symmons2008). The q-forward was linked to a longevity index based on England & Wales national male mortality for a range of different ages. The hedge was provided by J. P. Morgan and was novel not just because it involved a longevity index and a new kind of product, but also because it was designed as a hedge of value rather than a hedge of cash flow. In other words, it hedged the value of an annuity liability,Footnote ³⁸ not the actual individual annuity payments.

5.4.3. Formally, a q-forward is a contract between two parties in which they agree to exchange an amount proportional to the actual realised mortality rate of a given population (or sub-population), in return for an amount proportional to a fixed mortality rate that has been mutually agreed at inception to be payable at a future date (the maturity of the contract). In this sense, a q-forward is a swap that exchanges fixed mortality for the realised mortality at maturity, as illustrated in Figure 4. The variable used to settle the contract is the realised mortality rate for that population in a future period. In the case of hedging longevity risk in a pension plan using a q-forward, the plan will receive the fixed mortality rate and pay the realised mortality rate (and hence, over the term of the contract, locks in the future mortality rate it has to pay whatever happens to actual rates). The counterparty to this transaction, typically an investment bank, has the opposite exposure, paying the fixed mortality rate and receiving the realised rate.

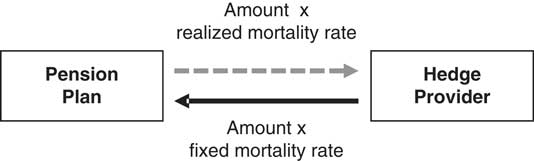
Figure 4 A q-forward exchanges fixed mortality for realised mortality at the maturity of the contract

Source: Coughlan et al. (Reference Coughlan, Epstein, Sinha and Honig2007b, Figure 1)

5.4.4. The fixed mortality rate at which the transaction takes place defines the “forward mortality rate” for the population in question. If the q-forward is fairly priced, no payment changes hands at the inception of the trade, but at maturity, a net payment will be made by one of the two parties (unless the fixed and actual mortality rates happen to be the same). The settlement that takes place at maturity is based on the net amount payable and is proportional to the difference between the fixed mortality rate (the transacted forward rate) and the realised reference rate. If the reference rate in the reference year is below the fixed rate (implying lower mortality than predicted), then the settlement is positive, and the pension plan receives the settlement payment to offset the increase in its liability value. If, on the other hand, the reference rate is above the fixed rate (implying higher mortality than predicted), then the settlement is negative and the pension plan makes the settlement payment to the hedge provider, which will be offset by the fall in the value of its liabilities. In this way, the net liability value is hedgedFootnote ³⁹ regardless of what happens to mortality rates. The plan is protected from unexpected changes in mortality rates.

5.4.5. Table 2 presents an illustrative term sheet for a q-forward transaction, based on a reference population of 65-year-old males from England & Wales. The q-forward payout depends on the value of the LifeMetrics Index for the reference population on the maturity date of the contract. The particular transaction shown is a 10-year q-forward contract starting on 31 December 2008 and maturing on 31 December 2018. It is being used by ABC Pension Fund to hedge its longevity risk over this period; the hedge provider is J. P. Morgan. The hedge is a “directional hedge” and will help the pension fund hedge its longevity risk so long as the mortality experience of the pension fund and the index change in the same direction.

Table 2 An Illustrative Term Sheet for a Single q-forward to Hedge Longevity Risk

Source: Coughlan et al. (Reference Coughlan, Epstein, Sinha and Honig2007b, Table 1).

5.4.6. On the maturity date, J. P. Morgan (the fixed-rate payer or seller of longevity risk protection) pays ABC Pension Fund (the floating-rate payer or buyer of longevity risk protection) an amount related to the pre-agreed fixed mortality rate of 1.2000% (i.e. the agreed forward mortality rate for 65-year-old English & Welsh males for 2018). In return, ABC Pension Fund pays J. P. Morgan an amount related to the reference rate on the maturity date. The reference rate is the most recently available value of the LifeMetrics Index. Settlement on 31 December 2018 will therefore be based on the LifeMetrics Index value for the reference year 2017, on account of the 10-month lag in the availability of official data. The settlement amount is the difference between the fixed amount (which depends on the agreed forward rate) and the floating amount (which depends on the realised reference rate).

5.4.7. Table 3 shows the settlement amounts for four realised values of the reference rate and a notional contract size of £50 m. If the reference rate in 2017 is lower than the fixed rate (implying lower mortality than anticipated at the start of the contract), the settlement amount is positive and ABC Pension Fund receives a payment from J. P. Morgan that it can use to offset an increase in its pension liabilities. If the reference rate exceeds the fixed rate (implying higher mortality than anticipated at the start of the contract), the settlement amount is negative and ABC Pension Fund makes a payment to J. P. Morgan which will be offset by a fall in its pension liabilities.

Table 3 An Illustration of q-Forward Settlement for Various Outcomes of the Realised Reference Rate

Source: Coughlan et al. (Reference Coughlan, Epstein, Sinha and Honig2007b, Table 1): A positive (negative) settlement means the hedger pays (receives) the net settlement amount.

5.4.8. It is important to note that the hedge illustrated here is structured as a “value hedge,” rather than as a “cash flow hedge.” A value hedge aims to hedge the value of the hedger’s liabilities at the maturity date of the swap. So although the swap has a duration of only 10 years, it nevertheless hedges that portion of the longevity risk in the hedger’s cash flows beyond 10 years that are reflected in mortality rates at time 10. This is achieved by exchanging a single payment at maturity. By contrast, a cash flow hedge hedges the longevity risk in each one of the hedger’s cash flows and net payments are made period by period as in Figure 2. The J. P. Morgan-Canada Life longevity swap is an example of a cash flow hedge, while the J. P. Morgan-Lucida q-forward is an example of a value hedge. The capital markets are more familiar with value hedges, whereas cash flow hedges are more common in the insurance world. Value hedges are particularly suited to hedging the longevity risk of younger members of a pension plan, since it is much harder to estimate with precision the pension payments they will receive when they eventually retire. The world’s first swap for non-pensioners (i.e. involving deferred members) took place in January 2011 when J. P. Morgan executed a value hedge in the form of a 10-year q-forward contract with the Pall (UK) pension fund.

5.4.9. The importance of q-forwards rests in the fact that they form basic building blocks from which other more complex, life-related derivatives can be constructed. When appropriately designed, a portfolio of q-forwards can be used to replicate and to hedge the longevity exposure of an annuity or a pension liability, or to hedge the mortality exposure of a life assurance book. We now provide an example.

5.4.10. A series of q-forward contracts, with different ages and maturities, can be combined to hedge a longevity swap. Initially assume that there is a complete market in these contracts for all ages and maturities. Suppose the contract involves swapping at time t a fixed cashflow, $\tilde{S}(t)$ , for the realised survivor index, S(t,x), where x is the age of the group being hedged at the inception of the swap. The fixed leg can be hedged using zero-coupon fixed-income bonds. The floating leg can be hedged approximately as follows. First, note that we can approximate the survivor index by expanding the cashflow in terms of the fixed legs of a set of q-forwards and their ultimate net payoffs (see Cairns et al., Reference Cairns, Blake and Dowd2008):

$$\eqalignno{ & S\left( {t,x} \right){\equals}\left( {1{\minus}q\left( {0,x} \right)} \right){\times}\left( {1{\minus}q\left( {1,x{\plus}1} \right)} \right){\times}...{\times}\left( {1{\minus}q\left( {t{\minus}1,x{\plus}t{\minus}1} \right)} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\equals}\prod\limits_{i{\equals}0}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,i,x{\plus}i} \right){\minus}\Delta \left( {i,x{\plus}i} \right)} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\approx\,\prod\limits_{i{\equals}0}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,i,x{\plus}i} \right)} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\minus}\mathop{\sum}\limits_{i{\equals}0}^{t{\minus}1} {\Delta \left( {i,x{\plus}i} \right)} \prod\limits_{j{\equals}0,j\,\ne\,i}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,j,x{\plus}j} \right)} \right)} $$

where Δ(i, x + i)=q(i, x + i)−q _F (0, i, x + i) and q _F (0, i, x + i)=q-forward mortality rate (the fixed rate). Here, Δ(i, x + i) is the net payoff on the q-forward per unit at time i + 1.

5.4.11. It follows that an approximate hedge (assuming interest rates are constant and equal to r per annum) for S(t, x) can be achieved by holding:

• ∙ $${\minus}\left( {1{\plus}r} \right)^{{{\minus}(t{\minus}1)}} \prod\nolimits_{j{\equals}0,\,j\,\ne\,1}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,j,x{\plus}j} \right)} \right)} $$ units of the 1-year q-forward;

• ∙ $${\minus}\left( {1{\plus}r} \right)^{{{\minus}(t{\minus}2)}} \prod\nolimits_{j{\equals}0,\,j\,\ne\,1}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,j,x{\plus}j} \right)} \right)} $$ units of the 2-year q-forward;

• ∙ …

• ∙ $${\minus}\prod\nolimits_{j{\equals}0,\,j\,\ne\,t{\minus}1}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,j,x{\plus}j} \right)} \right)} $$ units of the t-year q-forward.

5.4.12. In calculating these hedge quantities, we take account of the fact that, for example, the payoff at time 1 on the 1-year q-forward will be rolled up to time t at the risk-free rate of interest. Hence, the required payoff at time t needs to be multiplied by the discount factor (1 + r)^−(t−1). In a stochastic interest environment, a quanto derivative would be required. This is one that delivers a number of units, N, of a specified asset, where N is derived from a reference index that is different from the asset being delivered. In this context, N equals $${\minus}\Delta \left( {i,x{\plus}i} \right)\prod\nolimits_{j{\equals}0,\,j\,\ne\,i}^{t{\minus}1} {\left( {1{\minus}q_{F} \left( {0,j,x{\plus}j} \right)} \right)} $$ , and we deliver, at time i+1, N units of the fixed-interest zero-coupon bond maturing at time t, with a price P(i + 1,t) at time i + 1 per unit.

5.4.13. In the real world, a complete market in q-forward contracts does not exist and the hedge would have to be constructed from q-forward contracts with a more limited range of reference ages (e.g. 10-year age buckets) and maturities (e.g. out to 20 years at most). Nevertheless, the complete market hedge serves as a benchmark against which we can measure the effectiveness of hedges using a smaller number of q-forwards.

5.4.14. A related contract is the “S-forward” or “survivor” forward contract, which is based on the survivor index, S(t, x), which itself is derived from the more fundamental mortality rates. An “S-forward” is the basic building block of a longevity (survivor) swap first discussed in Dowd (Reference Dowd2003). A longevity swap is composed of a stream of S-forwards with different maturity dates. It could be used, for example, for covering early cashflows, in conjunction with a q-forward at time 10 to (partially) cover the later cashflows.Footnote ⁴⁰

5.5. Tail-Risk Protection (or Longevity Bull Call Spread)

5.5.1. To date there have been at least five publicly announced deals involving tail risk protection. The first two involved Aegon: one in 2012 was executed by Deutsche Bank and another in 2013 by Société Générale. The second two involved Delta Lloyd and Reinsurance Group of America (RGA Re) in 2014 and 2015, respectively. The most recent occurred in December 2017 between NN Life and Hannover Re and is similar to the Société Générale deal discussed below.

5.5.2. Société Générale’s tail risk protection structure was described in Michaelson & Mulholland (Reference Michaelson and Mulholland2014).Footnote ⁴¹ It is an index-based hedge using national population mortality data, but with minimal basis risk,Footnote ⁴² and is designed around the following set of principles (pp.30–31):

5.5.3. Basis risk will reduce hedge effectiveness and this will, in turn, reduce the allowable regulatory capital relief.Footnote ⁴³ However, basis risk with this product can be minimised if the hedger can customise three features of the hedge exposure:

• ∙ The hedger is able to select the age and gender of the “cohorts” (also known as model points) they want in the reference exposure. For example, the hedger selects an exposure totalling 70 cohorts – males and females aged 65–99 – to cover all the retired lives in the pension plan.

• ∙ The hedger is able to choose the “exposure vector,” i.e. the “relative weighting” of each cohort over time. This will equal the anticipated annuity payments for each cohort in each year of the risk period (see Table 4 for an example).

• ∙ The hedger is able to select an “experience ratio matrix,” based on an experience study of its underlying book of business. For each cohort, in each year of the risk period, a fixed adjustment is applied to the national-population mortality rate to adjust for anticipated differences between the mortality profile of the hedger’s book of business and the corresponding reference population. So if the hedger’s underlying lives are healthier than the general population, they will assign experience ratios of less than 100% to “scale down” the mortality rate applied in the payout (see Table 5 for an example).

Table 4 Exposure Vector: Relative Weighting of Cohorts Over Time

Source: Michaelson & Mulholland (Reference Michaelson and Mulholland2014, Exhibit 1).

Table 5 Experience Ratio Matrix

Source: Michaelson & Mulholland (Reference Michaelson and Mulholland2014, Exhibit 2).

5.5.4. A risk exposure period of 55 years – as shown in Tables 4 and 5 – is unattractive to capital markets investors for a number of reasons. Liquidity in this market is still low and would be completely absent at these horizons. The maximum effective investment horizon is no more than 15 years. Just as important, the risks are too great. The likely advances in medical science suggest that the range of outcomes for longevity experience will be very wide for an investment horizon of more than half a century.

5.5.5. To accommodate both an “exposure period” of 55 years or more and a “risk period” (or transaction length) of 15 years, the hedge programme uses a “commutation function” to “compress” the risk period. As explained in Michaelson & Mulholland (Reference Michaelson and Mulholland2014, pp. 32–33):

• ∙ Selecting an appropriate longevity risk model and establishing the initial parameterisation of the model using publicly available historical mortality data that exist as of the trade date. For a basic longevity model, the parameters that may be established, on a cohort-by-cohort basis, are (i) the current rate of mortality; (ii) the expected path of mortality improvement; and (iii) the variability in the expected path of mortality improvement.

• ∙ “Freezing” the longevity risk model, with regard to the related structure; but also defining, in advance, an objective process for updating the model’s parameters based on the additional mortality experience that will be reported over the risk period. A determination needs to be made as to which parameters are subject to updating, as well as the relative importance that will be placed on the historical data versus the data received during the risk period.

• ∙ Re-parameterising the longevity model by incorporating the additional mortality data reported over the life of the trade. This occurs at the end of the transaction risk period, once the mortality data for the final year in the risk period have been received.

• ∙ Calculating the present value of the remaining exposure using the re-parameterised version of the initial longevity model. This is done by projecting future mortality rates, either stochastically or deterministically, and then discounting the cash flows using forward rates determined at the inception of the transaction.

5.5.6. The benefit of this approach to the hedger is that “roll risk”Footnote ⁴⁴ is reduced, since, by taking account of actual mortality rates over the risk period, there will be a much more reliable estimate at the end of the risk period of the expected net present value of the remaining exposure than if only historical mortality rates prior to the risk period were used. The benefit to the investor is that the longevity model is known and not subject to change, so the only source of cash flow uncertainty in the hedge is the realisation of national population mortality rates over the risk period – see Figure 5.

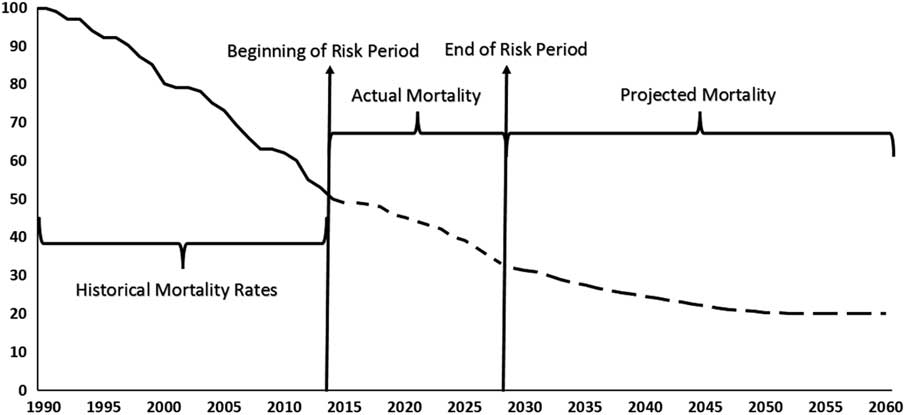
Figure 5 Mortality rates before, during and after the risk period

Note: Projected mortality rates are calculated using experience data available at end of the risk period.

Source: Michaelson & Mulholland (Reference Michaelson and Mulholland2014, Exhibit 3).

5.5.7. The hedge itself is structured using a long out-of-the money call option bull spread on future mortality outcomes. The spread has two strike prices or, using insurance terminology, an attachment point and an exhaustion point.Footnote ⁴⁵ These strikes are defined relative to the distribution of “final index values” calculated using the agreed longevity model. The final index value will be a combination of:

• ∙ The “actual” mortality experience of the hedger throughout the risk period which is calculated by applying the reported national population mortality rates to the predefined “exposure vector” and “experience ratio matrix” for each cohort in each year of the risk period, and accumulating with interest, using forward interest rates defined on the trade date.

• ∙ The “commutation calculation” that estimates the expected net present value of the remaining exposure at the end of the risk period, calculated using the re-parameterised version of the initial longevity model.

5.5.8. Given the distribution of the final index, the attachment and exhaustion points are selected to maximise the hedger’s capital relief, taking into account the investors’ (i.e. risk takers’) wish to maximise the premium for the risk level assumed. Investors might also demand a “minimum premium” to engage in the transaction. The intermediary – e.g. the investment bank – therefore needs to carefully work out the optimal amount of risk transfer, given both the hedger’s strategic objectives and investor preferences.

5.5.9. The hedger then needs to calculate the level of capital required to cover possible longevity outcomes with a specified degree of confidence. For example, if the “best estimate” of the longevity liability is $1bn, the (re)insurer may actually be required to issue $1.2bn, $200 m of which is reserve capital to cover the potential increase in liability due to unanticipated longevity improvement with 99% confidence.

5.5.10. The (re)insurer may then decide to implement a hedge transaction with a maximum payout of $100 m. This transaction would begin making a payment to the hedger in the event the attachment point is breached, and then paying linearly up to $100 m if the longevity outcome meets or exceeds the exhaustion point. This hedge provides a form of “contingent capital” from investors (up to $100 m of the $200 m required), enabling the hedger to reduce the amount of regulatory capital it must issue – see Figure 6.

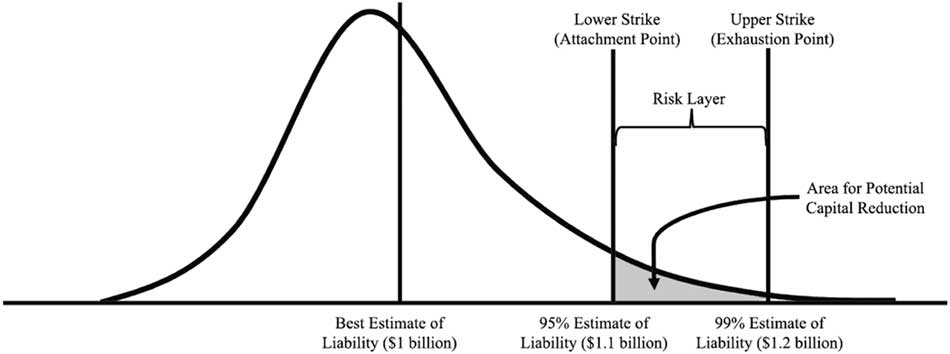
Figure 6 Distribution of the final index value and the potential for capital reduction

Source: Michaelson & Mulholland (Reference Michaelson and Mulholland2014, Exhibit 4) – not drawn to scale.

5.5.11. Tail risk protection was actually discussed in Living with Mortality in section 6.4 entitled “Geared Longevity Bonds and Longevity Spreads,” which we reproduce here. The geared longevity bond enables holders to increase hedging impact for any given capital outlay.

5.5.12. One way to construct such a bond would be as follows. Looking ahead from time 0, the payment on each date t can in theory range from 0 to 1 (times the initial coupon). However, again looking ahead from time 0, we can also suppose that the payment at time t (the survivor index, S(t,x); see paragraph 5.4.10 above) is likely to fall within a much narrower band, say S(t, x)∈[S _l (t), S _u (t)]. For example, if we are using a stochastic mortality model we could let S _l (t) and S _u (t) be the 2.5% and 97.5% percentiles of the simulated distribution of S(t, x). These simulated confidence limits become part of the contract specification at time 0.

5.5.13. We now set up a special purpose vehicle (SPV) at time 0 that holds S _u (t)−S _l (t) units of the fixed interest zero-coupon bond that matures at time t for each t=1,…,T (or its equivalent using floating-rate debt and an interest-rate swap). Suppose the SPV is financed by two investors A and B. At time t, the SPV pays: (i) S(t,x)−S _l (t) to A with a minimum of 0 and a maximum of S _u (t)−S _l (t); and (ii) S _u (t)−S(t,x) to B with a minimum of 0 and a maximum of S _u (t)−S _l (t).

5.5.14. The minimum and maximum payouts at each time to A and B ensure that the payments are always non-negative and can be financed entirely from the proceeds of the fixed-interest zero-coupon bond holdings of the SPV.

5.5.15. The payoff at t to A can equivalently be written as

$$\left( {S\left( {t,x} \right){\minus}S_{l} (t)} \right){\plus}max\left\{ {S_{l} \left( t \right){\minus}S\left( {t,x} \right),0} \right\}{\minus}max\left\{ {S\left( {t,x} \right){\minus}S_{u} \left( t \right),0} \right\}$$

that is, a combination of a long forward contract, a long put option on S(t, x) (or a “floorlet,” with a strike price that is lower than the at-the-money forward rate), and a short call on S(t, x) (or a “caplet” with a strike price that is higher than the at-the-money forward rate). The bond as a whole, therefore, is a combination of forwards, floorlets and caplets. Continuing with the option terminology, we can also observe that the payoff to investor A is often referred to as a long “bull call spread,” and for this reason we refer to the payoff in the current context as a long “longevity bull call spread.”

5.5.16. Let us suppose that, for each t, S _l (t) and S _u (t) have been chosen so that the value of the floorlet and the caplet are equal. In this case, the price payable at time 0 by investor A is equal to the sum of the prices of the T forward contracts paying S(t, x)−S _l (t) at times t=1,…,T. This is equal to (i) the price for the longevity bond paying S(t, x) at times t=1,…,T, minus (ii) the price for the fixed-interest bond paying S _l (t) at times t=1,…,T. This structure therefore gives investors a similar exposure to the risks in S(t, x) for a lower initial price. For this reason, we describe the collection of longevity bull spreads as a geared longevity bond.

5.5.17. As an alternative, S _u (t) might be set to 1, meaning that the caplet has zero value (S(t, x) cannot be bigger than 1). With this structure, investor A has full protection against unanticipated improvements in longevity, but gives away any benefits from poorer longevity than anticipated.

5.5.18. It is important to note in the above construction that there is a smooth progression in the division of the coupon payments between the counterparties over the range of S(t, x). This is preferable to a contract that has a jump in the amount of the payment as S(t, x) crosses some threshold: as often happens with such contracts as barrier options, arguments can often arise as to whether the particular threshold was crossed or not. Such difficulties are avoided with the smooth progression.

5.5.19. The bond described here is a variation on the Société Générale structure where the payoff at T depends only on the single survivor index S(T, x). In the more general case, the payoff depends on the values of S(1, x),…,S(T, x) and the forecast values at T of S(T + 1, x),S(T + 2, x),….

6.1. Overview

Lucida and Canada Life implemented two very different kinds of capital markets longevity hedges in 2008. Lucida executed a standardised hedge linked to a population mortality index, whereas Canada Life executed a customised hedge linked to the actual mortality experience of a population of annuitants. Aegon’s hedges with Deutsche Bank in 2012 and with Société Générale in 2013 were also index hedges, but they were designed to minimise the basis risk involved.Footnote ⁴⁶ It is important to understand the differences between index and customised hedges. It is also important to understand, measure and manage the basis risk in index hedges. This, in turn, will have implications for regulatory capital relief.

6.2. Index Versus Customised Hedges

6.2.1. Standardised index-based longevity hedges have some advantages over the customised hedges that are currently more familiar to pension funds and annuity providers. In particular, they have the advantages of simplicity, cost and greater potential for liquidity. But they also have obvious disadvantages, principally the fact that they are not perfect hedges and leave a residual basis risk (see Table 6) that requires the index hedge to be carefully calibrated.

Table 6 Standardised Index Hedges Versus Customised Hedges

Source: Coughlan (Reference Coughlan2007a).

6.2.2. Coughlan et al. (Reference Coughlan, Epstein, Sinha and Honig2007b) show that a liquid, hedge-effective market could be built around just eight standardised q-forward contracts with:

• ∙ a specific maturity (e.g. 10 years);

• ∙ two genders (male, female);

• ∙ four age buckets (50–59, 60–69, 70–79, 80–89).

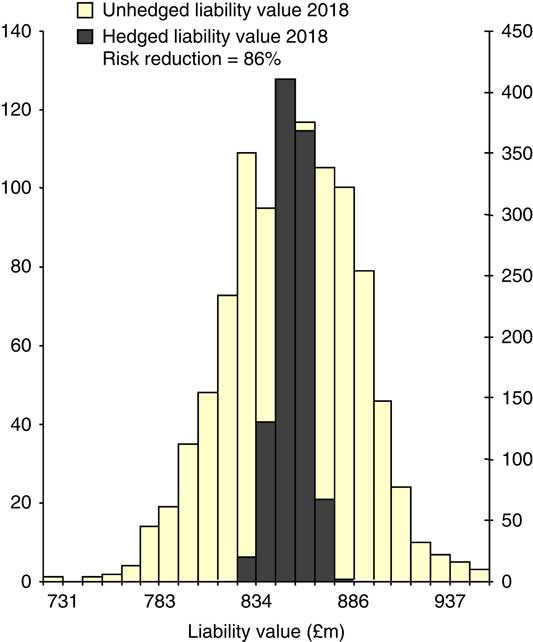
6.2.3. Figure 7 presents the mortality improvement correlations within the male 70–79 age bucket which is centred on age 75 (Coughlan et al., Reference Coughlan, Epstein, Ong, Sinha, Hevia-Portocarrero, Gingrich, Khalaf-Allah and Joseph2007c). These figures show that the correlations (based on graduated mortality rates) are very high. Consequently, a tailored hedge using, say, 10 q-forwards on ages 70–79 will be only marginally more effective than a single q-forward using a standard 70–79 age bucket. Coughlan (Reference Coughlan2007a) estimates that the hedge effectiveness (of a value hedge) is around 86% (i.e. the standard deviation of the liabilities is reduced by 86%, leaving a residual risk of 14%) for a large and well-diversified pension plan or annuity portfolio: see Figure 8.Footnote ⁴⁷

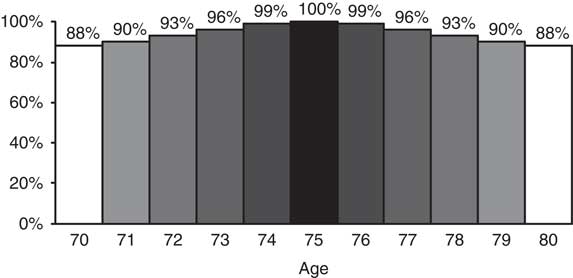
Figure 7 Five-year mortality improvement correlations with England & Wales males aged 75

Source: Coughlan et al. (Reference Coughlan, Epstein, Ong, Sinha, Hevia-Portocarrero, Gingrich, Khalaf-Allah and Joseph2007c, Figure 9.6).

Figure 8 The hedge effectiveness of q-forwards

Source: Coughlan (Reference Coughlan2007a).

6.2.4. In order to keep the number of contracts to a manageable level, individual contracts use the average (or “bucketed”) mortality across 10 ages rather than single ages. This averaging has positive and negative effects. On the one hand, the averaging reduces the basis risk that arises from the non-systematic mortality risk that is present in crude mortality rates, even at the population level.Footnote ⁴⁸ On the other hand, it introduces some basis risk depending on the specific age-structure of the population being hedged. This we now discuss in more detail.

6.3. Basis Risk

6.3.1. Basis risk is the residual risk associated with imperfect hedging where the movements in the underlying exposure are not perfectly correlated with movements in the hedging instrument. Basis risk and its quantification have recently attracted the attention of both academics and practitioners (e.g. Li & Hardy, Reference Li and Hardy2011; Cairns et al., Reference Cairns, Blake, Dowd and Coughlan2014; Longevity Basis Risk Working Group, 2014; Villegas et al., Reference Villegas, Haberman, Kaishev and Millossovich2017; Li et al., Reference Li, Tickle, Tan and Li2017; Cairns & El Boukfaoui, Reference Cairns and El Boukfaoui2018).

6.3.2. Within the context of longevity risk hedging, a number of sources of basis risk arise: population basis risk; base-table risk; structural risk; restatement risk; and idiosyncratic risk.

6.3.3. Population basis risk is, perhaps, the form of basis risk that most readily comes to mind when considering an index based longevity hedge. Specifically, a hedger might choose to use a hedging instrument that is linked to a different population from its own population that it wishes to hedge. This is most common where the hedging instrument is linked to an index based on national mortality rates, while the hedger’s own population is a distinctive sub-population with different characteristics from the national average. As a consequence, underlying mortality rates might not just be at a different level from that of the national population, but rates of improvement in both the short and long term might not be perfectly correlated. Modelling and understanding the differences between two populations is an active and rapidly developing subject of research.Footnote ⁴⁹

6.3.4. Base-table risk concerns how accurately hedgers and also receivers of longevity risk are able to assess the mortality base table for both the hedger’s own population and the national population. Whether or not base-table risk contributes to residual risk for the hedger then depends on the nature of the longevity hedge. At one end of the spectrum, from the perspective of the hedger, a customised longevity swap leaves the hedger with no base-table risk, while the receiver is exposed and should charge a higher price to reflect this extra risk. In contrast, for an index-based hedge, base-table risk will be relevant. Base-table risk will then make a more significant contribution to total basis risk if the hedger’s own population is small or the time horizon of the hedge is short.

6.3.5. Structural risk relates to the design of the hedging instrument, and it can arise even if there is no population basis risk or base-table risk:

• ∙ The hedging instrument might have a non-linear payoff as a function of the underlying risk. This includes contracts with an option-type payoff structure such as the bull call spread in Michaelson & Mulholland (Reference Michaelson and Mulholland2014) and Cairns & El Boukfaoui (Reference Cairns and El Boukfaoui2018), leaving residual risk both below and above the attachment and exhaustion points. It also includes q-forwards: these do not include any optionality, but liability cashflows are typically non-linear combinations of the underlying mortality rates.

• ∙ The hedging instrument might have a finite maturity, meaning that the longevity risk that emerges after the maturity date is a residual risk that cannot be hedged.

• ∙ The reference ages embedded in the hedging instruments might not allow exact matching of the ages in the hedger’s population.

• ∙ The number of units of the hedging instrument (i.e. the hedge ratio) might not be optimal (i.e. might not minimise residual risk). This might be either unavoidable or unintentional (e.g. through the use of a poorly calibrated model).

• ∙ Hedging instruments might not incorporate an inflation linkage and so might not match well with realised pension plan or annuity benefit increases.

In general, structural risk can be adjusted, for example, through the choice of: attachment and exhaustion points; the maturity date; the reference ages; the number of q- or S-forwards; and careful calibration and optimisation using the chosen stochastic mortality model.

6.3.6. Restatement risk concerns the possibility that official estimates of the national population or death counts might be revised up or down, with potential impacts on index-based hedge payoffs (Cairns et al., Reference Cairns, Blake, Dowd and Kessler2016). Restatements will often impact on previously stated mortality rates (especially following a decennial census). Index-based longevity hedges will probably link contractually to the first announcement of a mortality rate, meaning that the restatement of past mortality rates will not alter past payments and hence introduce an additional risk. However, restatements will also have an impact on future estimated population numbers and consequent mortality rates. The future risks and impacts of such restatements can be assessed through use of the same methodology for identifying phantoms proposed in Cairns et al. (Reference Cairns, Blake, Dowd and Kessler2016).

6.3.7. Idiosyncratic riskFootnote ⁵⁰ is primarily linked to sampling variation and its financial impact within the hedger’s population. As with some other examples of basis risk, the impact of idiosyncratic risk will depend on the nature of the hedge (indemnity versus other forms). Given the evolution of the systematic risk in the underlying mortality rates, individuals will either die or survive independently of each other. Proportionately, this risk is larger for smaller pension funds. The level of idiosyncratic risk is also dependent on the heterogeneity in pension amounts (leading to concentration risk): for example, a 1,000-member pension plan in which 10% of the members are directors (or “big cheeses”) who generate 90% of the liabilities will be more risky than a 1,000-member plan with equal pensions.

6.3.8. Finally, as remarked in Cairns (Reference Cairns2014), accurate assessment of basis risk is one part of the process of choosing the best hedge. First, one needs to identify the different options for hedging.Footnote ⁵¹ Second, the risk appetite of the hedger needs to be properly assessed. Third, there needs to be an accurate assessment of the basis risk under each hedge. Fourth, prices need to be established for each hedge. Fifth, the combination of price, basis risk and risk appetite then point to a best choice out of all of the options available to the hedger.Footnote ⁵² Cairns (Reference Cairns2014) also highlights that no single hedging option is best for all pension plans. Everything else being equal, customised hedges are more likely to be preferred to index hedges by: smaller pension plans rather than larger (due to the greater idiosyncratic risk); and pension plan sponsors that are more risk averse. Also, certain hedging options (e.g. longevity swaps) are currently only available to pension plans with sufficiently large liabilities.

6.4. Other Types of Basis Risk

Other forms of basis risk might arise if a pension plan seeks to hedge the longevity risk associated with a group of active or deferred members, rather than retired members. These groups bring additional risks, including member options (such as lump sum commutation, trivial commutation, early/late retirement, increasing a partner’s benefits at the expense of the member’s benefits, and pension increase exchanges), partner status at retirement or member death and salary risk. The plan’s quantum of exposure to longevity risk depends on how these risks turn out, a risk that itself is not hedgeable.

7.1. Overview

Another risk in Table 6 is counterparty credit risk. This is the risk that one of the counterparties to, say, a longevity swap contract defaults owing money to the other counterparty. When a swap is first initiated, both counterparties might expect a zero excess profit or loss.Footnote ⁵³ But over time, as a result of realised mortality rates deviating from the rates that were forecast at the time the swap started, one counterparty’s position will be showing a profit and the other will be showing an equivalent loss. The insurance industry addresses this issue via regulatory capital and the capital markets deal with it via collateral.

7.2. Regulatory Capital

7.2.1. The regulatory regime covering insurance companies domiciled in the UK is governed by the Solvency II Directive which came into effect in January 2016 and is used to set regulatory capital requirements.

7.2.2. Regulatory capital is the level of capital or Own Funds required by an insurer’s regulatory authority, the PRA in the UK. Solvency II begins with a calculation of the insurer’s liabilities, known as technical provisions, which comprises a “best estimate” of the liabilities plus a risk margin – in the case where the liability cannot be reliably measured and/or suitably hedged. The sum of the best estimate and risk margin can be thought of as the market consistent value or fair value. On top of this, insurers must issue additional risk-based capital to meet first the Minimum Capital Requirement (MCR) and then the Solvency Capital Requirement (SCR).

7.2.3. A major objective of Solvency II is to value all assets and liabilities on a market-consistent basis and to ensure that the regulatory capital that insurance companies issue reflects all the unhedged risks on their balance sheets. The capital should be sufficient to ensure that an insurance company can either (i) survive the next 12 months with a 99.5% probability or (ii) survive a set of prescribed stress tests. The amount required can be determined using either a stochastic internal model or through the use of the standard stress test, which in the case of longevity risk is a sudden 20% reduction in mortality rates across all ages. For a 65-year old UK male, this corresponds approximately to a 1.5-year increase in life expectancy or a 7% increase in pension liabilities.

7.2.4. A consequence of any market-consistent approach is that both assets and liabilities are prone to market volatility. Insurance companies invest in long-term illiquid assets, like infrastructure, real estate and equity release mortgages, to reduce asset price volatility, and in corporate bonds to benefit from the credit and illiquidity premia embodied in their higher returns compared with government bonds.

7.2.5. In the case of long-term liabilities, such as annuities and buy-outs, short-term asset price volatility can be partially offset by “matching adjustments” (MAs). MAs are part of Solvency II regulations that depart from a market-consistent approach, by allowing insurersFootnote ⁵⁴ to estimate the illiquidity premium – inherent in the asset portfolio if it contains such illiquid assets – to be added to the risk-free rate for the purposes of discounting liabilities. To do this, the insurer needs to allocate a specific pool of assets to the liability, where the assets are selected to match the cash-flow characteristics of the liability. The assets need to be matched for the entire term of the liability, in which case the liability can be valued using the higher but less volatile MA-adjusted discount rate. Because both the level and volatility of the liability calculated using this approach are now lower, lower levels of Own Funds and hence SCR are needed. However, because of longevity risk and the dearth of long-maturity longevity-linked assets available to hold in the portfolio, the asset match can never be perfect. The higher MA-adjusted discount rate is reduced somewhat to allow for this and the level of Own Funds correspondingly raised. A particular example is non-pensioner members of pension plans who have both greater longevity risk and more optionality than pensioner members. Both these factors lower the MA-adjusted discount rate and, by raising the level of Own Funds, increase the cost of providing deferred annuities to the pension plan or buying out this segment of the pension plan. Insurers also make use of reinsurance to reduce the volatility of liabilities and this will again have an effect on Own Funds.

7.2.6. One possible implication of Solvency II is that insurers might migrate away from the current cash-flow hedging paradigm towards the value-hedging paradigm. Specifically, insurers might aim to hedge their liability in one year’s time as a way to reduce their SCR under Solvency II. This requires comparison of liability and hedge instrument values one year ahead.

7.2.7. Despite Solvency II, some pension plans considering de-risking remain concerned about the financial strength of some insurers, which is why consultants, such as Barnett Waddingham, have launched an insurer financial strength review service, providing information on an insurer’s structure, solvency position, credit rating and key risks in their business model.

7.2.8. Regulatory capital deals principally with the credit risk of the insurer.Footnote ⁵⁵ Conversely, the insurer faces credit risk from the pension plan in the case of, say, a longevity swap, and collateral would need to be posted to deal with this.

7.3. Collateral

7.3.1. The role of collateral is to reduce if not entirely eliminate counterparty credit risk in both capital market transactions and insurance contracts.

7.3.2. Collateral in the form of high-quality securities needs to be posted by the loss-making counterparty to cover such losses. However, the collateral needs to be funded and the funding costs will depend on the level of interest rates. Further, the quality of the collateral and the conditions under which a counterparty can substitute one form of collateral for another need to be agreed. This is done in the credit support annex (CSA) to the ISDAFootnote ⁵⁶ Master Agreement that establishes the swap. The CSA also specifies how different types of collateral will be priced.

7.3.3. All these factors are important for determining the value of the swap at different stages in its life. Biffis et al. (Reference Biffis, Blake, Pitotti and Sun2016) use a theoretical model to show that the overall cost of collateralisation in mortality or longevity swaps is similar to or lower than those found in the interest-rate swaps market on account of the diversifying effects of interest rate and longevity risks – which are to a first order uncorrelated risks. In practice, agreeing the value of the collateral involves an iterative process. Valuing the fixed leg is generally straightforward, but there can be differences of opinion in valuing the floating leg. It is typical in reinsurance contract negotiations for both sides to recommend a basis. If the difference is too far apart, both sides agree to bring in either one or two external experts. If only one is used, both sides are bound by their assessment. If two are used and they are close, both sides agree to split the difference: if they are still too far apart, both sides will allow the experts to appoint an agreed third expert.

9.1. Overview

It is clear from the solutions we have described above that mortality models play a critical role in their design and pricing (see, e.g. Figures 3 and 6). There are three classes of stochastic mortality model in use (with some models straddling more than one class):

• ∙ extrapolative or time series models;

• ∙ process-based models – which examine the biomedical processes that lead to death;

• ∙ explanatory or causal models – which use information on factors which are believed to influence mortality rates such as cohort (i.e. year of birth), socio-economic status, lifestyle, geographical location, housing, education, medical advances and infectious diseases.

Most of the models currently in use are in the first of these classes and we will concentrate on these in this section.

9.2. Extrapolative or Time Series Models – Single Population Variants

9.2.1. There are four classes of time-series-based mortality model in use. First is the Lee-Carter class of models (Lee & Carter, Reference Lee and Carter1992), which makes no assumption about the degree of smoothness in mortality rates across adjacent ages or years. Second is the Cairns–Blake–Dowd (CBD) class of models (Cairns, Blake & Dowd, Reference Cairns, Blake and Dowd2006), which builds in an assumption of smoothness in mortality rates across adjacent ages in the same year (but not between years).Footnote ⁵⁹ Third is the P-splines model (Currie et al., Reference Currie, Durban and Eilers2004) which assumes smoothness across both years and ages.Footnote ⁶⁰ Finally, there is the Age-Period-Cohort (APC) model which has its origins in medical statistics (Osmond, Reference Osmond1985; Jacobsen et al., Reference Jacobsen, Keiding and Lynge2002), and was first introduced in an actuarial context by Renshaw & Haberman (Reference Renshaw and Haberman2006). Other features have also jumped from one class to another with the resulting genealogy mapped out in Figure 9. The first two classes of models have also been extended to allow for a cohort effect.Footnote ⁶¹ All these models were subjected to a rigorous analysis in Cairns et al. (Reference Cairns, Blake, Dowd, Coughlan, Epstein, Ong and Balevich2009, 2011a) and Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan, Epstein and Khalaf-Allah2010b, 2010c). The models were assessed for their goodness of fit to historical data and for both their ex-ante and ex-post forecasting properties.

Figure 9 A genealogy of stochastic mortality models

Source: Adapted from Cairns (Reference Cairns2014)

9.2.2. Cairns et al. (Reference Cairns, Blake, Dowd, Coughlan, Epstein, Ong and Balevich2009) used a set of quantitative and qualitative criteria to assess each model’s ability to explain historical patterns of mortality: quality of fit, as measured by the Bayes Information Criterion (BIC); ease of implementation; parsimony; transparency; incorporation of cohort effects; ability to produce a non-trivial correlation structure between ages; and robustness of parameter estimates relative to the period of data employed. The study concluded that a version of the CBD model allowing for a cohort effect was found to have the most robust and stable parameter estimates over time using mortality data from both England & Wales and the US. This model (usually referred to as “M7”) is now the keystone of one of the two approaches recommended by the Life and Longevity Markets Association (LLMA)Footnote ⁶² (Longevity Basis Risk Working Group, 2014, Villegas et al., Reference Villegas, Haberman, Kaishev and Millossovich2017, and Li et al., Reference Li, Tickle, Tan and Li2017).

9.2.3. Cairns et al. (Reference Cairns, Blake, Dowd, Coughlan, Epstein and Khalaf-Allah2011a) focused on the qualitative forecasting properties of the modelsFootnote ⁶³ by evaluating the ex-ante plausibility of their probability density forecasts in terms of the following qualitative criteria: biological reasonableness;Footnote ⁶⁴ the plausibility of predicted levels of uncertainty in forecasts at different ages; and the robustness of the forecasts relative to the sample period used to fit the models. The study found that while a good fit to historical data, as measured by the BIC, is a promising starting point, it does not guarantee sensible forecasts. For example, one version of the CBD model allowing for a cohort effect produced such implausible forecasts of US male mortality rates that it could be dismissed as a suitable forecasting model. This study also found that the Lee-Carter model produced forecasts at higher ages that were “too precise,” in the sense of having too little uncertainty relative to historical volatility. The problems with these particular models were not evident from simply estimating their parameters: they only became apparent when the models were used for forecasting. The other models (including the APC model) performed well, producing robust and biologically plausible forecasts.

9.2.4. It is also important to examine the ex post forecasting performance of the models. This involves conducting both backtesting and goodness-of-fit analyses. Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan, Epstein and Khalaf-Allah2010b), undertook the first of these analyses. Backtesting is based on the idea that forecast distributions should be compared against subsequently realised mortality outcomes and if the realised outcomes are compatible with their forecasted distributions, then this would suggest that the models that generated them are good ones, and vice versa. The study examined four different classes of backtest: those based on the convergence of forecasts through time towards the mortality rate(s) in a given year; those based on the accuracy of forecasts over multiple horizons; those based on the accuracy of forecasts over rolling fixed-length horizons; and those based on formal hypothesis tests that involve comparisons of realised outcomes against forecasts of the relevant densities over specified horizons. The study found that the Lee-Carter model, the APC model and the CBD model (both with and without a cohort effect) performed well most of the time and there was relatively little to choose between them. However, another version of the Lee-Carter model allowing for a cohort effect repeatedly showed evidence of instability.Footnote ⁶⁵

9.2.5. Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan, Epstein and Khalaf-Allah2010c) set out a framework for evaluating the goodness of fit of stochastic mortality models and applied it to the same models considered by Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan, Epstein and Khalaf-Allah2010b). The methodology used exploited the structure of each model to obtain various residual series that are predicted to be independently and identically distributed (iid) standard normal under the null hypothesis of model adequacy. Goodness of fit can then be assessed using conventional tests of the predictions of iid standard normality. For the data set considered (English & Welsh male mortality data over ages 64–89 and years 1961–2007), there are some notable differences amongst the various models, but none of the models performed well in all tests and no model clearly dominates the others. In particular, all the models failed to capture long-term changes in the trend in mortality rates. Further development work on these models is therefore needed. It might be the case that there is no single best model and that some models work well in some countries, while others work well in other countries.

9.2.6. The CBD model appears to work well in England & Wales for higher ages, and Figures 10–12 present three applications of the model using ONS data for England & Wales.

Figure 10 Longevity fan chart for 65-year-old English & Welsh males

Source: Own calculations.

Figure 11 Cohort survivor fan chart for 65-year-old English & Welsh males

Source: Own calculations.

Figure 12 Cohort mortality fan chart for 65-year-old English & Welsh males

Source: Own calculations.

9.2.7. The first (Figure 10) is a longevity fan chart (Dowd et al, Reference Dowd, Blake and Cairns2010a), which shows the increasing funnel of uncertainty concerning future life expectancies out to 2052 of 65-year-old males from England & Wales.Footnote ⁶⁶ By 2047, life expectancy from age 65 is centred around 23 years, shown by the dark central band: an increase of 4 years on the expectation for the year 2017. The different bands within the fan correspond to 5% bands of probability with the lower and upper boundaries at the 5% and 95% quantiles. Adding these together, the whole fan chart shows the 90% confidence interval for the forecast range of outcomes. We can be 90% confident that by 2047, the life expectancy of a 65-year-old English & Welsh male will lie between 21.3 and 24.3. This represents a huge range of uncertainty. Since every additional year of life expectancy at age 65 adds around 4–5%Footnote ⁶⁷ to the present value of pension liabilities, the cost of providing pensions in 2060 could be 7–8% higher than the best estimate for 2047 made in 2017.

9.2.8. The second is a survivor fan chart (Blake et al., Reference Blake, Cairns and Dowd2008), which shows the 90% confidence interval for the survival rates of English & Welsh males who reached 65 at the end of 2016. Figure 11 shows that there is relatively little survivorship risk before age 75: a fairly reliable estimate is that 20% of this group will have died by age 75.Footnote ⁶⁸ The uncertainty increases rapidly after 75 and reaches a maximum just after age 90, when anywhere between 27% and 38% of the original cohort will still be alive. We then have the long “tail” where the remainder of this cohort dies out some time between 2042 and 2062.

9.2.9. The third is a mortality fan chart which shows the 90% confidence interval for 65-year old English & Welsh males who reached 65 at the end of 2016. Figure 12 shows that there is an increasingly low probability of surviving year to year at very high ages, even with predicted mortality improvements.

9.2.10. By building off a good mortality forecasting model estimated using data from an objective, transparent and relevant set of mortality indices, fan charts provide a very useful tool for both quantifying and visually understanding longevity, survivor and mortality risks.

9.2.11. One key problem that extrapolative models have is their difficulty in differentiating between a genuine change in the trend of mortality rates and a temporary blip in mortality rates until some time after the change has occurred. In 2016, the UK Office for National Statistics reported that longevity improvements rates at very high ages have slowed down since 2011; but it is not yet clear whether this is a genuine change in the long-term trend, a short-term austerity-driven adjustment, or just the result of a purely random deviation from the previous trend.Footnote ⁶⁹ Nevertheless, it prompted a debate in the UK in 2016 about the reliability of life expectancy projections. Mortality improvements in UK males averaged 0.6% p.a. over the preceding four years, compared with 3.2% p.a. in the decade before and 1.5–2% between 1995 and 2000.Footnote ⁷⁰ In response to a possible trend change, the UK Continuous Mortality Investigation (CMI) has lowered its estimate of both male and female life expectancy at age 65 over 4 consecutive years, as Table 7 shows.

Table 7 UK Life Expectancy at Age 65

Source: Continuous Mortality Investigation.

9.2.12. In October 2016, Tim Gordon, head of longevity at Aon Hewitt, said: “This is the most extreme reversal in mortality improvement trends seen in the past 40 years. What was initially assumed by many actuaries to be a blip is increasingly looking more like an earlier-than-expected fall-off in mortality improvements. The industry is currently trying to digest all the implications of this emerging information and – inevitably – it is taking time to feed through into insurance and reinsurance pricing.” Others say that this could just be “noise.” Matt Wilmington, director of pension risk transfer at Legal & General (L&G), points out that: “Two years doesn’t make a trend – it’s very volatile from year to year. If we had another five years where we saw far fewer deaths than expected, then we might start to see fairly significant changes, but where we are now, there’s not enough to persuade us – or many of the pension plans we work with – that there’s a vast reversal in trend in terms of life expectancy just yet.” Despite this, Aon Hewitt said that there was sufficient dislocation in the pricing of longevity swaps that pension plans should consider delaying transactions until the market corrects. By the middle of 2017, Aon Hewitt reported that the longevity market was back in sync.Footnote ⁷¹ However, Tim Gordon also warned against attempts to time the market: “Timing the longevity market in the same way you would time an equity market is extremely difficult, and plans could be in danger of missing opportunities now if they did that.” The difference in mortality improvement rates before and after 2011 is equivalent to a difference in liabilities of 1% or 4 months of pension payments for every retiree: UK pension liabilities would be £25bn lower if the future mortality improvement rate were 1% rather than 3%.Footnote ⁷²

9.2.13. Consultant Barnett Waddingham has put forward the suggestion that higher health and social care spending between 2000 and 2010 (which grew at an average annual real rate of 4%) may have caused a blip in longevity estimates by accelerating improvements. Since 2009, health spending has grown at just 1% per annum in real terms, social care spending has fallen in real terms, and there have been lower mortality improvements – although this correlation does not imply causation.Footnote ⁷³

9.3. Extrapolative or Time Series Models – Multi-Population Variants

9.3.1. There are a number of reasons why it might be appropriate or desirable to model two or more populations simultaneously. First, a pension plan might often be relatively small in relation to the national population; it might have a relatively short run of data (e.g. relatively limited coverage of ages, or only a few calendar years of observations) or simply have a lot of sampling variation. In contrast, many national populations have a much longer run of data. By modelling the two populations in tandem and exploiting the correlations between the two, it might be possible to achieve better quality forecasts for the pension plan. Second, the use of multiple population mortality models enables more accurate modelling of the relationships between two or more groups that are directly of interest (e.g. males and females; assured lives and annuitants in a life insurer’s book of business; life insurance portfolios in different countries, etc.). This will lead to better consistency in forecasts as well as, for example, an assessment of the diversification benefits of having less-than-perfectly correlated groups of lives. Third, multi-population modelling is essential for any institution seeking to hedge its exposure to longevity risk using index-based hedging instruments: the model is required to assess the level of basis risk in the transaction.

9.3.2. The development of multi-population mortality models has lagged single population modelling quite considerably partly due to a lack of good quality sub-population datasets (the CMI assured lives dataset being a notable exception). The Human Mortality Database (HMD) has data for many countries and offers a useful starting point, but sub-population data present particular challenges that are often not present in international data (e.g. shorter runs of data, smaller population sizes, etc.). In the demography literature, Li and Lee (Reference Li and Lee2005) laid out some key foundations: in particular, the principle of coherence. The ratio of mortality rates in two populations can and will vary over time. However, the principle of coherence requires that this ratio should not diverge over time towards zero or infinity.Footnote ⁷⁴ In the actuarial literature, key early contributions have been made by Cairns et al. (Reference Cairns, Blake, Dowd, Coughlan, Epstein and Khalaf-Allah2011b), Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan and Khalaf-Allah2011), Li and Hardy (Reference Li and Hardy2011) and Börger et al. (Reference Börger, Fleischer and Kuksin2013).Footnote ⁷⁵ More recently, Villegas et al. (Reference Villegas, Haberman, Kaishev and Millossovich2017) carried out an extensive review of both existing and potential new multi-population models. Despite the general popularity of the Li & Lee (Reference Li and Lee2005) model, their model has been found to be quite unsuitable for some actuarial applications by both Villegas et al. (Reference Villegas, Haberman, Kaishev and Millossovich2017) and Enchev et al. (Reference Enchev, Kleinow and Cairns2017). Specifically, applications that require a stochastic assessment of longevity risk (e.g. measurement of basis risk or diversification benefits) require models that have a plausible correlation term structure: the Li and Lee model fails on this criterion.Footnote ⁷⁶

9.3.3. To satisfy the principle of coherence, Cairns et al. (Reference Cairns, Blake, Dowd, Coughlan, Epstein and Khalaf-Allah2011b) make use of a mean-reverting stochastic spread that allows for different trends in mortality improvement rates in the short-run, but parallel improvements in the long run. This study uses a Bayesian framework that allows the estimation of the unobservable state variables that determine mortality and of the parameters of the stochastic processes that drive those state variables to be combined into a single step. The key benefits of this include a dampening of the impact of Poisson variation in death counts,Footnote ⁷⁷ full allowance for parameter uncertainty, and the flexibility to deal with missing data.

9.3.4. Dowd et al. (Reference Dowd, Cairns, Blake, Coughlan and Khalaf-Allah2011) employ a “gravity” model to achieve coherence using an iterative estimation procedure.Footnote ⁷⁸ The larger population is modelled independently (similar to the approach recommended by Villegas et al., Reference Villegas, Haberman, Kaishev and Millossovich2017), but the smaller population is modelled in terms of spreads (or deviations) relative to the evolution of the larger population. To satisfy the principle of coherence, the spreads in the period and cohort effects between the larger and smaller populations depend on gravity or spread reversion parameters for the two effects. The larger the two gravity parameters, the more strongly the smaller population’s mortality rates move in line with those of the larger population in the long run.

9.3.5. In their comprehensive comparison of two-population models, Villegas et al. (Reference Villegas, Haberman, Kaishev and Millossovich2017) find that two models satisfy best their criteria for a good two-population model: the common age effect model (Kleinow, Reference Kleinow2015) with a cohort effect added; and a variant of the CBD family labelled as M7-M5.Footnote ⁷⁹ Additionally, they offer useful guidance on the minimum quality of data for the sub-population: a minimum annual exposure of 20,000–25,000 lives over at least 8–10 years,Footnote ⁸⁰ although Bayesian methods offer the potential to relax these criteria somewhat (e.g. Chen et al., Reference Chen, Cairns and Kleinow2017, Cairns et al., Reference Cairns, Blake, Dowd, Coughlan, Epstein and Khalaf-Allah2011b, Reference Cairns, Kallestrup-Lamb, Rosenskjold, Blake and Dowd2017a).

9.4. Process-Based and Causal Models

9.4.1. Until recently, these classes of models were not widely used, since the relationships between biomedical and causal factors and underlying death rates were not sufficiently well understood and because the underlying data needed to build the models were unreliable. This has begun to change.

9.4.2. In 2012, RMS launched a series of mortality indices and models via a platform called RMS LifeRisks. The platform allows life insurance companies and pension funds in the UK, the USA, France, Germany, Holland and Canada to model and manage their exposure to longevity and mortality risks, taking into account recent medical research and social change projections. There are two principal models.Footnote ⁸¹

9.4.3. The first model is the RMS longevity risk model. This is the base model used to project mortality and variations in mortality during normal conditions when there are no extreme mortality events. The projections depend on a number of so-called “vitagion categories” or individual sources of mortality improvement (see Figure 13). The five categories used by RMS are: lifestyle trends, including smoking prevalence; health environment; medical intervention; regenerative medicine, such as stem cell research, gene therapy and nanomedicine; and the retardation of ageing, including telomere shortening and caloric restriction.

Figure 13 Timeline into the future

Note: Structural modelling of medical-based mortality improvement explores the timing, magnitude and impact of different phases of new medical advances on the horizon.

Source: RMS (2010) “Longevity Risk.”

9.4.4. The second model is the RMS infectious diseases model. This is used to estimate the additional mortality arising from the outbreak of certain infectious diseases, e.g. pandemic influenza. Both models were used in pricing the Kortis bond (see section 5.2) and an outbreak of something like influenza would be the most likely reason for the attachment point being reached during the life of the bond.

9.4.5. Academic researchers have recently begun experimenting with the introduction of causal variables in their mortality models (e.g. Hanewald, Reference Hanewald2011; Gaille & Sherris, Reference Gaille and Sherris2011; Alai et al., Reference Alai, Arnold (-Gaille) and Sherris2014a; Villegas & Haberman, Reference Villegas and Haberman2014; Gourieroux & Lu, Reference Gourieroux and Lu2015; Cairns et al., Reference Cairns, Kallestrup-Lamb, Rosenskjold, Blake and Dowd2017a). Practitioners also started to use post code as a measure of socio-economic class (SEC) in their proprietary mortality models, especially for pricing annuities. An early example is Richards (Reference Richards2008).

9.4.6. In 2008, Club Vita, a UK longevity data and analytics company, was set up with the express purpose of improving the socio-economic modelling of mortality data, allowing the segmentation of projections by SEC. To illustrate, cancer mortality related to smoking (such as larynx, oropharynx, oral cavity and lung) is more commonly associated with the lowest SEC, while cancer mortality related exposure to the sun (malignant melanoma) is more commonly associated with the highest SEC. Segmented longevity trend models have improved in recent years as a result of new insights from medical science and a greater understanding of cause of death for each SEC. The benefits of this to a pension plan have been an improved (and sometimes lower) best estimate of life expectancy (due to a more accurate socio-economic breakdown of the plan’s membership) with less uncertainty in the base table. The benefits to an insurer seeking new business have been refined pricing, better assessment of diversification, more effective risk selection, and increased competitiveness (Baxter & Wooley, Reference Baxter and Wooley2017). However, there is still an ongoing debate around using trend assumptions by SEC. For example, Jon Palin of Barnett Waddingham argues: “The evidence is less clear on the level of historical mortality improvements in pension schemes and other segments of the population, and to what extent a different assumption should be made for them.”Footnote ⁸²

9.4.7. The emergence of new multi-population datasets with socio-economic subdivisions is also beginning to offer much greater potential for the development of reliable and robust multi-population models. For example, Cairns et al. (Reference Cairns, Kallestrup-Lamb, Rosenskjold, Blake and Dowd2017a) make use of Danish population data subdivided using a measure of affluence that combines wealth and income, and utilising this data, they develop a 10-population CBD-type stochastic model over the age range 55–94. With ten sub-populations to analyse, they avoid excessive model complexity by assuming a relatively simple model for correlations between sub-populations. A Bayesian framework is exploited to dampen the effect of sampling variation that is inherent in the ten relatively small sub-populations. It is anticipated that in the near future this and other datasets will become publicly available to allow researchers to develop alternative models, as well as further road-testing existing models.

10.1. Overview

In this section, we introduce some applications of the extrapolative mortality models introduced in the previous section: practical implementation of stochastic mortality models; determination of the longevity risk premium; estimating regulatory capital relief with a hedge in place; and comparison of alternative longevity risk management options. We begin by considering different types of users of these models.

10.2. Users of Stochastic Mortality Models

10.2.1. The following are potential users (directly or indirectly) of stochastic mortality models: insurers and reinsurers; regulators (e.g. the PRA); pension plans; specialist and general investors; actuaries and actuarial consultants; and software providers (e.g. Longevitas).

10.2.2. Insurers and reinsurers have a variety of reasons for using stochastic mortality models. Arguably, the principal reason is that they form part of an overall package of good enterprise risk management alongside stochastic models for other major risks, all augmented by a range of appropriate stress and scenario tests. Insurers can then use stochastic models to assess their economic capital requirements. Closely linked to this, many insurers are moving towards the use of stochastic models to assess regulatory capital requirements. For example, the PRA strongly encourages the use of stochastic mortality models with the standard one-year horizon under Solvency II (Prudential Regulatory Authority, 2015, 2016). Multi-population models also offer the potential for insurers to assess the diversification benefits resulting from exposure to different portfolios of lives (males/females, smokers/non-smokers, assurances/annuities, multi-country, etc.), with subsequent reductions, for example, in regulatory capital. Lastly, insurers might wish to use stochastic models to compare different options for the management of longevity risk. Depending on in-house capability, insurers might develop their own suite of stochastic mortality models, or use external expertise. This might come in the form of ready-to-use mortality software that is employed in-house by appropriately trained staff, or by contracting external consultants to perform stochastic analyses.

10.2.3. Regulators will not, typically, be direct users of stochastic mortality models. However, they do need to be sufficiently knowledgeable in their use (including awareness of the assumptions and limitations of each model) in order to be able to assess how they are being used by life insurers. Additionally, they need to be able to give periodic guidance on the use of stochastic models, including which models are, or are not, acceptable (see, for example Prudential Regulatory Authority, 2015, 2016).

10.2.4. The acceptance of systematic longevity risk will, in general, form part of the core risk taking activity of an insurer up to a level that is consistent with its overall risk appetite. In contrast, acceptance of longevity risk is not generally part of the core business of the typical sponsor of an occupational pension plan (nor indeed is investment and interest-rate risk). Nevertheless, systematic longevity risk is present and therefore requires careful attention. Large pension plans have the resources to assess their exposure to longevity risk through the use of both stochastic modelling and deterministic scenarios: again as part of a wider programme of integrated risk management. As with insurers, this might be done in-house, but more often this would be a service provided by the plan’s actuarial advisers. Smaller pension plans are less likely to have the financial resources to carry out a full stochastic assessment of longevity risk. However, there is the potential for the longevity risk research community to develop a small range of deterministic longevity scenarios (expressed as adjustments to the preferred best estimate forecast) that capture the essence of realistic extreme stochastic scenarios. On the other hand, consultancies now tend to have fairly streamlined processes for running off stochastic projections in order to illustrate the magnitude of each element of the longevity risk; these would typically be based on simplified pension benefits but would additionally reflect the most important aspects of the scheme, such as membership age, gender, and pension amounts. Such scenarios and projections should contrast favourably with the poorly formulated 20% stress test required under Solvency II (see Cairns & El Boukfaoui, Reference Cairns and El Boukfaoui2018). Models, therefore, can help plans determine appropriate target funding levels and contribution rates, as well as assess the risks associated with meeting these targets. Finally, as remarked earlier, use of stochastic models is recommended as a way to help choose between alternative longevity risk management options (including retention of the risk).

10.2.5. Pension plans also need to assess the potential future funding levels that might result from future uncertain investment returns, interest rate changes and changes in longevity. Stochastic mortality models can be used as part of a larger internal modelling exercise to assess uncertainty in funding levels. Larger plans will have the resources to carry out such an exercise. For smaller plans, stochastic models can again be used by actuarial consultants to generate a small number of deterministic extreme scenarios that can be applied to a range of smaller pension plans.

10.2.6. Specialist and general investors in longevity risk (e.g. ILS investors, hedge funds, private equity investors, sovereign wealth funds, endowments and family offices) and other receivers of longevity risk (e.g. reinsurers) are only likely to invest in this risk if it offers an acceptable risk premium, taking into account the low correlation between longevity risk and financial market risks and hence the potential diversification benefits from including longevity-linked products in an investment portfolio. This will be reflected in the price of the transaction at the outset relative to a best estimate or expected value. A rigorous approach to this requires a set of stochastic models to assess how much risk there is around the expected payoff.Footnote ⁸³ In a competitive market, the size of the risk premium will reflect each potential investor’s other exposures: for example, a reinsurer might be satisfied with a lower risk premium for longevity risk if they have offsetting life assurance exposures.

10.3. Practical Implementation of Stochastic Mortality Models

10.3.1. It is common practice in the UK to use different methodologies for setting central forecasts and for risk assessment around that central forecast. For example, life insurers might use the CMI_2016 model (formally known as the CMI mortality projection model, calibrated using data up to 2016) to frame their central forecast and calculate best estimate liabilities. They then follow PRA guidelines (Prudential Regulatory Authority, 2015, 2016) and use stochastic mortality models to assess, proportionately, how much risk there is around that best estimate (Cairns et al., Reference Cairns, Blake and Dowd2017b). The use of CMI_2016 allows users some control over future improvement rates and, in key elements, requires the exercise of sound judgement (e.g. in setting the long-term rate of improvement). This contrasts with the more objective statistical approach prevalent in stochastic mortality modelling. Under the stochastic approach, the central forecast is determined by: the choice of model; the choice of time series model (or equivalent) for forecasting period and cohort effects; and the historical calibration period. These elements are ones that can be chosen objectively using standard statistical methods (see, for example Cairns et al., Reference Cairns, Blake, Dowd, Coughlan, Epstein, Ong and Balevich2009; Richards et al., Reference Richards, Currie, Kleinow and Ritchie2017). No further judgement is required once these selections have been made.

10.3.2. Current research is attempting to close the gap between the two approaches. For example, Richards et al. (Reference Richards, Currie, Kleinow and Ritchie2017) focus on the Age Period Cohort Improvements (APCI) model that underpins the historical calibration of the CMI_2016 model, and propose a coherent stochastic approach for forecasting. On the other hand, Cairns et al. (Reference Cairns, Blake and Dowd2017b) discuss an approach that closes the gap between the CMI central forecast and the mean trajectory under the objective statistical approach. This involves giving the user some control over setting the short and long term central trends in the period and cohort effects in a stochastic model. With some minor constraints applied to the historical calibration of the CMI model, the adapted stochastic model and the CMI_2016 projections can produce consistent central forecasts, allowing users to place greater reliance on the outputs of the stochastic model.

10.4. Determining the Longevity Risk Premium

10.4.1. As just discussed, the provider of any longevity hedge requires a premium to assume longevity risk. This means that the forward rate agreed at the start of any q-forward contract will be below the anticipated (expected) mortality rate on the maturity date of the contract. Similarly, the implied forward life expectancy in any longevity swap will be higher than the anticipated (expected) life expectancy. Figure 14 shows a typical relationship between the expected and forward mortality rate curves and the risk premium for a particular cohort currently aged 65.Footnote ⁸⁴ Figure 15 shows the same for a particular age (in this case 65-year-old English & Welsh males) for years 2005–2025: the further into the future, the more uncertainty there is in the mortality rate and the bigger the risk premium.

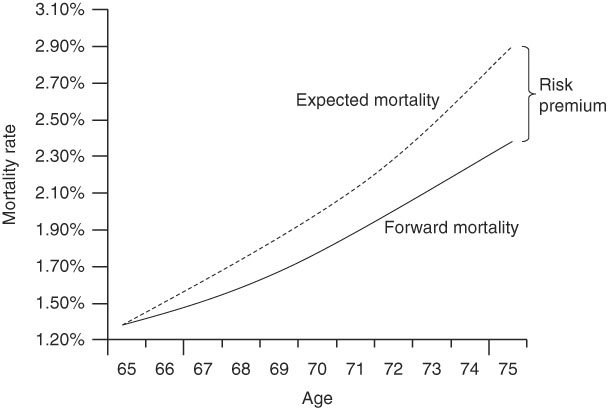
Figure 14 Cohort expected and forward mortality rate curves for a cohort currently aged 65 and q-forward maturity at age 75

Note: Lines are illustrative only.

Source: Adapted from Loeys et al. (Reference Loeys, Panigirtzoglou and Ribeiro2007, Chart 9).

Figure 15 Expected and forward mortality rate curves for 65-year-old English & Welsh males, 2005–2025

Note: Lines are illustrative only.

Source: Adapted from Coughlan (Reference Coughlan2007a).

10.4.2. As remarked above, a stochastic model can be used to assess how much uncertainty there is in the underlying hedge instrument, and then this information can be used to determine an appropriate risk premium. There are different approaches to setting the price, for example: discounting the expected payoff at an appropriate risk-adjusted discount rate that reflects the assessed level of risk; or calculating a risk-adjusted expected payoff prior to discounting at the risk-free rate. When applied to the pricing of multiple contracts, not all frameworks will produce consistent prices over a range of contracts and maturities. However, the method of risk adjustment proposed by Cairns et al. (Reference Cairns, Blake and Dowd2006) using an explicit market price of risk for each period effect and for each year is one that does guarantee pricing consistency. This can be used to determine what might be thought of as mid-market prices, around which participants in the market can set buying and selling prices that reflect the degree of market illiquidity.

10.5. Estimating Regulatory Capital Relief

10.5.1. In section 7.2 above, we discussed regulatory capital. Under Solvency II, an insurer’s regulatory capital can be reduced if its liabilities are appropriately hedged.

10.5.2. This necessitates bringing the relevant regulatory authority on board sooner rather than later, as experience in the Netherlands shows. The Dutch financial regulator, the Dutch National Bank (DNB), assesses longevity hedges on a case-by-case basis. A particular case is insurance, pensions and investments firm Delta Lloyd’s two index-based longevity hedges.Footnote ⁸⁵ Delta Lloyd had its Solvency II capital ratio reduced by 14 percentage points at the end of 2015 following “intense discussions.” This was due to a disagreement with the DNB about the inclusion of risk margin relief on the two longevity hedges beyond the duration of the hedges. The DNB treats an index-based hedge as a financial instrument, whereas it treats a customised hedge as a reinsurance contract. It wanted the index-based hedges to be restructured to “ensure reinsurance treatment,” otherwise Delta Lloyd faced a further 7 percentage points deduction from its Solvency II ratio.

10.5.3. In June 2016, the DNB clarified its position. It agreed that for an index-based swap, capital relief will be proportional to the risk transfer. However, it felt that some previous index-based deals had been of too short duration, too out-of-the-money and not a good match for actual liabilities.Footnote ⁸⁶

10.5.4. A detailed account of how to calculate regulatory capital relief in a longevity hedge can be found in Cairns and El Boukfaoui (Reference Cairns and El Boukfaoui2018).Footnote ⁸⁷ They describe a flexible framework that blends practical issues with current academic modelling work. Key elements include careful assessment of basis risk, subdivided into population basis risk and other sources. They then consider a specific longevity hedge with a call option spread payoff structure and analyse the impact on regulatory capital. A key conclusion is that the balance between population basis risk and other sources of basis risk (especially structural basis risk) is highly dependent on the exhaustion point of the underlying option. For example, in a Solvency II setting, if the exhaustion point is close to the 99.5% quantile of the underlying risk, the recognition of population basis risk can have a significant effect on the regulatory capital required. In contrast, if the exhaustion point is somewhat below the 99.5% quantile (e.g. 95%), then population basis risk has a negligible impact on the amount of regulatory capital relief.Footnote ⁸⁸ In the latter case, therefore, the index-based hedge acts in a very similar way to a reinsurance arrangement with similar attachment and exhaustion points in terms of its impact on regulatory capital. The authors conclude that hedgers need to consider carefully the terms of an index-based hedge (in the case considered, the attachment and exhaustion points and the maturity date), to ensure the best outcome. Further, in light of the evidence in the previous two paragraphs, insurers should discuss their plans with their local regulator before proceeding with a hedge. Bearing this in mind, Cairns & El Boukfaoui (Reference Cairns and El Boukfaoui2018) outline a clear set of steps that can be used to document regulatory capital relief calculations with the recommendation that these steps be followed as a way to facilitate discussions with local regulators. This includes a requirement to document clearly the structure of the two-population stochastic mortality model, how this is calibrated, how death rates get extrapolated to high ages, and how central forecasts will be determined at future valuation dates incorporating new information up to that valuation date.

10.6. Comparison of Risk Management Options

Good risk management practice includes consideration of a variety of viable options for reducing exposure to longevity risk, and stochastic models have a key quantitative role, alongside qualitative criteria, in the process that leads to choosing one option over another. Cairns (Reference Cairns2014) outlines some of the issues. The stochastic model can be used in a consistent way to evaluate a hedger’s longevity risk profile with and without each of the hedging options in place. The range of options itself might be constrained by the size of the liability to be hedged (for example customised longevity swaps have typically been restricted to larger pension plans) but should, in the first instance, include both customised and index-based hedges. Any analysis should also take into account a hedger’s exposure to idiosyncratic risk. Once residual risk has been evaluated, the hedger is then in a position to compare the different options. This should take into account the hedger’s general risk appetite as well as the underlying premium for a hedge (section 10.4) and future requirements for adjustments to the hedge (e.g. a buy-in used prior to a full buy-out). Cairns (Reference Cairns2014) discusses, in a stylised fashion, how these multiple inputs can result in different final decisions: one size does not fit all.Footnote ⁸⁹

12.1. Overview

A number of potential solutions were suggested in the 2006 Living with Mortality paper:

• ∙ Longevity bond types (e.g. zero-coupon longevity bonds, deferred longevity bonds, principal-at-risk longevity bonds and longevity spread bonds).

• ∙ Mortality, longevity and annuity futures.

• ∙ Mortality options, longevity caplets and floorlets.

• ∙ Mortality swaptions.

These were direct translations from already existing capital market instruments, but so far none of these, apart from a single longevity spread bond (i.e. Kortis) and a few longevity bull call spreads constructed using longevity caplets and floorlets (e.g. the 2013 Aegon deal with Société Générale), have been introduced in the longevity risk transfer market. In this section, we look at two potential new solutions that might have a greater chance of being introduced in the near term.

12.2. Potential New Solution: Longevity-Linked Securities

12.2.1. A perceived problem with the EIB/BNP Paribas longevity bond was that the reference index might not be sufficiently highly correlated with a hedger’s own mortality experience (as a result of population basis risk). An alternative instrument – denoted a longevity-linked security (LLS)Footnote ¹⁴⁹ – deals, at least partly, with this problem. The concept was inspired by the design of mortgage-backed securities.

12.2.2. The LLS is built around a special purpose vehicle. Individual hedgers on one side of the contract (e.g. a pension plan or an annuity provider) arrange longevity swaps with the SPV using their own mortality experience at rates that are negotiated with the SPV manager. The swapped cashflows are then aggregated and passed on to the market. Bondholders gain if mortality is heavier than anticipated.

12.2.3. It might be felt that the aggregate cashflows themselves lack transparencyFootnote ¹⁵⁰ in which case the SPV might link cashflows to an accepted reference index. The difference between this and the aggregated swap cashflows is a basis risk that is borne by the SPV manager.

12.2.4. This type of arrangement is illustrated in Figure 17 where the intermediary in this case is a reinsurer, which transacts customised longevity swaps with a set of hedgers. In this example, there are three hedgers, A, B and C (but there could, of course, be many more). Hedger A wishes to swap the risky longevity-linked cashflows L _A (t) for a series of pre-determined cashflows. The agreement with the SPV manager is to swap floating L _A (t) for fixed $\tilde{L}_{A} (t)$ for t=1,…,T, with the fixed leg set at a level that results in the swap initially having zero value at time 0. Similarly, hedger B swaps floating L _B (t) for fixed $\tilde{L}_{B} (t)$ , and hedger C floating L _C (t) for fixed $\tilde{L}_{C} (t)$ . The SPV itself invests in AAA-rated, fixed-interest securities of appropriate duration or uses floating rate notes plus an interest-rate swap.

Figure 17 Cash flows under a LLS

12.2.5. The LLS bond holders pay an initial premium that is used to buy the fixed-interest securities and to pay an initial commission to the SPV manager. The bond holders in return receive coupons and, possibly, a final repayment of principal that is linked to a reference index, X(t), that matchesFootnote ¹⁵¹ as closely as possible the combined cashflows, rather than to L _A (t), L _B (t) or L _C (t). Any differences accrue to or are paid by the SPV manager. The bond holders will not normally be hedgers themselves, so they will expect a fair premium over market fixed-interest rates in return for assuming the longevity risk.

12.2.6. Finally, the LLS might take the form of a catastrophe (or cat) bond (similar to the Kortis bond). In this case, the repayment of principal would be determined by the value of an index-based underlying, with appropriate attachment and exhaustion points.

12.2.7. To be more concrete, the underlying index X(t) that the LLS makes reference to is derived from, e.g. national population mortality rates, and is constructed in a way to achieve the optimal balance between hedge effectiveness for the reinsurer, within the cat bond structure, and the risk-return profile to investors. For a cat bond with attachment and exhaustion points AP and EP, the payoff at maturity will be the full bond nominal, N, if X(T) < AP, N(1−(X(T)−AP)/(EP−AP)) if AP≤X(T) < EP, and 0 if EP≤X(T).

12.2.8. The hedge is most likely to be effective if the reinsurer takes on a balanced and well diversified group of transactions with the primary hedgers (A, B and C above). For example, if the primary reinsurance transactions are wholly with blue collar pension plans, then an index-based LLS will be much less effective for the reinsurer. A low level of population basis risk turns out not to require exact matching of the national population (e.g. the aggregation of A, B and C). For example, Cairns et al. (Reference Cairns, Kallestrup-Lamb, Rosenskjold, Blake and Dowd2017a) demonstrate that an aggregated portfolio that covers 80% of the population but is also heavily skewed in value terms towards wealthier and healthier people can have a correlation with the national population that is well above 95%.

12.2.9. The marketing of LLS to ILS investors has great potential, following the introduction of comprehensive UK regulations for ILS in 2017, particularly if it takes the cat bond structure familiar to such investors, according to consultants Hymans Robertson. This is because longevity risk is becoming better understood and its volatility and correlation with other asset classes is low. Hymans Robertson argues that “Bulk annuity insurers could use [ILS] to provide additional capital to finance large deals (particularly where reinsurance is expensive or difficult to obtain) or to optimise their capital positions by rebalancing the risks on their balance sheets.” With the ILS investor base broadening all the time and an increasing amount of capital flowing into the market from other sophisticated investor sources, there is a growing pool of capital for which longevity or bulk-annuity linked risks might be attractive.Footnote ¹⁵²

12.3. Potential New Solution: Reinsurance Sidecars

12.3.1. Another potential solution is the reinsurance sidecar – which is a way to share risks with new investors when the latter are concerned about the ceding reinsurer having an informational advantage.

12.3.2. Formally, a reinsurance sidecar is a financial structure established to allow external investors to take on the risk and benefit from the return of specific books of insurance or reinsurance business. It is typically set up by existing (re)insurers that are looking to either partner with another source of capital or set up an entity to enable them to accept capital from third-party investors (Kessler et al., Reference Kessler, Bugler, Nicenko and Gillis2016).

12.3.3. It is established as a SPV, with a maturity of 2–3 years. It is capitalised by specialist insurance funds, usually by preference shares, though sometimes in the form of debt instruments. It reinsures a defined pre-agreed book of business or categories of risk. Liability is limited to assets of the SPV and the vehicle is unrated.

12.3.4. The benefit to insurers is that sidecars can provide protection against exposure to peak longevity risks,Footnote ¹⁵³ help with capital management by providing additional capacity without the need for permanent capital, and can provide an additional source of income by leveraging underwriting expertise. The benefit to investors is that they enjoy targeted non-correlated returns relating to specific short-horizon risks and have an agreed procedure for exiting; investors can also take advantage of temporary price hikes, but without facing legacy issues that could affect an investment in a typical insurer.

12.3.5. Figure 18 shows a typical sidecar structure.

Figure 18 Typical sidecar structure

Source: PFI.

12.3.6. There are a number of challenges to the use of sidecars in the longevity risk transfer market. There is the tension between the long-term nature of longevity risk and investor preference for a short-term investment horizon. There are also regulatory requirements on cedants, affecting their ability to generate a return. These include: the posting of prudent collateral, the underlying assets in the SPV must generate matching cash flows, the risk transfer must be genuine, and the custodian/trustee must be financially strong. There is also a risk to cedants of losing capital relief if regulatory requirements are not met or they change.

12.4. Why Could These Potential Solutions Be Successful Now?

The principal reason why these solutions might be more successful now in a way that they were not a decade ago is the capacity constraint in the (re)insurance industry – it does not have the capital or experienced personnel to take on unlimited longevity risk. The only long-term solution to this capacity constraint is to bring in new investors from the capital markets (i.e. to transfer the risk to the capital markets). These investors will include ILS investors, hedge funds, private equity investors, sovereign wealth funds, endowments, family offices and other investors seeking asset classes that have low correlation with existing financial assets. However, two issues need to be resolved. First, the hedger needs assurance that the solution sold to these investors provides an effective hedge. Second, these investors need some assurance that they are not going to be sold a “lemon.”Footnote ¹⁵⁴ There have been many attempts over the last decade to provide both types of assurance – without any real success. This time it might be – and certainly needs to be – different. An early sign of success for the reinsurance sidecar structure came at the beginning of 2018 when RGA Re and RenaissanceRe, announced a new start-up named Langhorne Re, which will target in-force life and annuity business. The new company has secured $780 m of equity capital from RGA, RenaissanceRe and third-party sidecar investors, including pension funds and other life companies.Footnote ¹⁵⁵