One of the more surprising things a sixteenth-century owner of an expensive folio volume might do was to take a sharp knife and cut it to pieces. John Blagrave's 1585 The Mathematical Jewel, in fact, demands nothing less. This book, which introduced an elaborate instrument of Blagrave's design for performing astronomical calculations, included woodcuts that were specifically intended to be cut out and used as surrogates for the brass original: ‘get very fine pastboord … and then spred your paste very fine thereon, & quickly laying on this picture & clappe it streight into a presse’.Footnote 1 ‘This picture’ refers to the full-page diagram printed near the front of the book, which can, as Blagrave says, be compiled with other diagrams to make a functioning instrument. In one surviving copy this has been done in a rather idiosyncratic manner: the plates have been cut out, pasted onto card and then pasted back into the inside of the book's front cover (Figure 1).Footnote 2

Figure 1. A copy of John Blagrave's The Mathematical Jewel (London, 1585), with the plates removed, carefully cut out, pasted onto board and mounted inside the book's front cover. Cambridge University Library, LE.28.5. By permission of the Syndics of Cambridge University Library.
We have long known that early modern readers were active in their approach to texts, bringing social, political and practical ambitions to bear on their reading and annotating practices.Footnote 3 But the case of Blagrave's cut-out Jewel takes things one step further. The book demands not ‘readers’ but ‘users’ – or perhaps better ‘practitioners’.Footnote 4
If, instead of attacking Blagrave's book, we settle down to read it instead, the impression that this is a fundamentally practical treatise deepens.Footnote 5 In addition to suggesting that the Jewel might be made by cutting out the diagram, Blagrave also includes instructions for making the instrument in wood or brass. Even to engage with Blagrave's text is to be taken into the world of craft and technique.
No sooner have the categories of practice and practitioners been introduced than it is necessary to call them into question. Sure enough, the owner of the paper instrument shown in Figure 1 could carry out many of the functions of the Jewel – a purportedly novel instrument that was in fact a modification of a type of astrolabe popularized in Europe earlier in the sixteenth century.Footnote 6 Blagrave's title page boasts that the instrument could solve problems in ‘Astronomy, Cosmography, Geography, Topography, Navigation, Longitudes of Regions, Dyalling, Sphericall triangles, Setting figures, and briefely of whatsoever concerneth the Globe or Sphere’. But was the Jewel really intended for use while travelling, or for making astronomical observations, or in day-to-day time telling? Perhaps the intention was instead to teach the disciplines themselves through instrumental practice?
In short, the case of Blagrave's Jewel raises fundamental questions about teaching, learning and practice, and how these relate to printed material, especially instrument manuals and treatises on the mathematical arts, which contain a variety of graphical tools, and often give instructions on the manufacture of complex devices.
In what follows I develop the argument that books were sites for mathematical practice. I mean this quite literally: advanced work in a range of disciplines could be carried out in the margins and between the covers of books, and geometrical tools could be transferred onto separate sheets and into commonplace books. Just as instruments themselves could be studied and ‘read’ as if they were texts, instrument books could be ‘used’ as functional devices.Footnote 7 In both cases, however, we need to be specific about context and intention. The textual analogy for instruments works when we know who approached instruments in this way, and to what end they were studied. Medieval armillary spheres, for instance, were useful to illustrate the ‘doctrine of the sphere’ in university classes.Footnote 8 When and how, then, did books become instrumentalized? This paper is an attempt to answer that question, focusing on the English case in the period during which the trade in instruments developed, roughly c.1570–c.1670.
Through the linked techniques of scale drawing, trigonometry and projective geometry, the mathematical (or mathematicized) world could be inscribed in two dimensions; pop-ups and volvelles supplied depth and movement, and diagrams could be worked on or transferred off the page onto solid supports to be taken out into the field or on board ship. While institutions for the promotion and teaching of practical mathematics were either non-existent or in their infancy, books provided an informal syllabus: a means by which individuals from a range of backgrounds could take part in a political/technological project that promised a new relationship between individual learning and state power.Footnote 9 My particular focus here is ‘instrument books’ – texts that are either substantially dedicated to describing the use of instruments, or that were designed to accompany some specific device. These were hybrid texts, and they created hybrid users. Books had certain kinds of functionality built in to them, and the mathematical arts developed in ways that were amenable to the development of paper technologies.
As a contribution to the study of manuals and handbooks, my intention is to bring together three areas of scholarship: the history of practical mathematics, the bibliography of early modern science and recent trends in the study of the material text. For the first of these we now have sophisticated accounts of the ways in which practitioners used diagrams, models and working instruments to bind together a loosely connected set of disciplines including cosmography, astronomy, astrology, geography, surveying, navigation and gunnery.Footnote 10 From the beginning of research in this area books have played a central role, as in the pioneering bio-bibliographic work of E.G.R. Taylor and Francis Johnson.Footnote 11 Recent studies have focused in particular on the role of images and diagrams, and the way that these can function practically and imaginatively, for instance as ‘geometrical tools’.Footnote 12 Finally, book history has turned to the ‘material text’ and the sociology of reading, and these developments offer much for historians of science.Footnote 13
In order to construct my argument about paper and practice I first offer a definition of instrument books: here the thorny issue of ‘making’ is crucial to the establishment of the genre. Offering instructions for practice was a well-established topos in how-to manuals, but this should not be taken at face value; conversely, however, there are reasons to believe that texts and images played an important role in the workshop. I then turn to the materiality of paper and the central importance of certain kinds of diagrammatic representation, especially projective geometry, the technique underlying Blagrave's instrument. Here the use of texts becomes a hybrid activity, making instruments of books and artisans of scholars. Distinctions are not wholly collapsed, however. Once we understand the ways in which mathematical practice could be conducted on paper we can read instrument books anew, with attention paid to the precise role of description, construction and use in the way they are arranged. This allows us to appreciate variety and complexity in a largely unexplored corpus of texts.
Of instrument books
John Blagrave's ‘Jewel’ – which refers both to the book and to the instrument – and Peter Apian's self-classifying Instrument-Buch (1533) notwithstanding, the genre that I am discussing here requires some explanation. Like Blagrave's work, the earliest manuscript and printed instrument books on the Continent had been dedicated to the astrolabe; these were supplemented in the early sixteenth century by separate treatises on sundials, and descriptions of instruments of various kinds in texts like Gregor Reisch's Margarita philosophica (first published in 1496).Footnote 14 From the beginning, two important trends were set: the inclusion of workable instruments in textbooks, as in Regiomontanus's 1474 Calendarium, which concludes with a group of paper instruments,Footnote 15 and the description of the making of instruments in materials other than paper, as in Johann Stöffler's influential Elucidatio fabricae ususque astrolabii (first published in 1513).Footnote 16
In England – a latecomer to practical mathematics – the Continental pattern was reversed.Footnote 17 The first texts to deal with instruments were not specific treatises or manuals, but were instead works that advocated the mathematical arts in general, or included instruments in reforms to a specific discipline like surveying or navigation. Only following Blagrave's intervention in 1585 did a group of instrument-specific texts appear, most of them written by the London lecturer Thomas Hood.Footnote 18 Thomas Fale's 1592 Horologiographia is another important milestone as this was, belatedly, the first text dedicated to sundials published in the English language.
By the end of the sixteenth century these and other areas of practice – and even such apparently non-mathematical pursuits as medicine and horticulture – were all incorporated into the project of practical mathematics, and in each case instruments played a central role.Footnote 19 Hence in Blagrave's imagery we can see that the embodiments of the disciplines are given representative instruments (see Figure 1, corners of the woodcut): Geometry has dividers and geometrical solids, Astronomy has a cross-staff and armillary sphere, Navigation depicts a man using a cross-staff on board ship, and Cosmography has a celestial globe and plumb line. Instruments were also central to the pedagogy of practical mathematics. Armillary spheres and astrolabes taught the principles of positional astronomy and cosmography.Footnote 20 Celestial and terrestrial globes served the same purpose, adding a particular focus on navigation as a part of cosmography, and came to symbolize the interconnection of worldly power and celestial harmony. Even the construction and use of sundials went far beyond the simple functions of time telling, as we shall see below.
For historians of the early modern period, instrument books have been of interest primarily as sources for the development of the mathematical arts, and, more narrowly, for the development of the trade in mathematical instruments.Footnote 21 Attempts to make use of instrument books for broader historical purposes have so far been tentative, raising useful questions but providing few answers. Adam Mosley, for instance, relates the difficulty of discerning the purposes of instrument books to the more general problem of interpreting instruments themselves.Footnote 22 For Mosley, local cultures of learning and practice supervene on generic considerations, so the task is to define contexts and plot their development and interaction. A different approach is taken by Mario Biagioli, who briefly discusses instrument books in his essay on patenting activity in the early instrument trade. The issue that detains Biagioli is that by teaching the making and use of instruments, manuals ‘defy assumptions about both artisanal secrecy and economic logic’.Footnote 23 For Blagrave the case is particularly acute, as he was writing at precisely the time that the first generation of instrument-makers opened shops in London. Did the model of openness not compromise the nascent trade? Biagioli's answer is no: books provided so much general support for the mathematical arts that giving up craft secrets was a small price to pay.
Whether or not this proposition is borne out, by focusing on the presence of instructions for making instruments Biagioli has, in my view, hit upon the central issue in the instrument-book genre. Whatever the local context of production and reception of an instrument book, the meaning of the text was moderated by what could and could not be made.
How (not) to make a mathematical instrument
Ignoring for now the paper instrument shown above, how easy would it have been to make Blagrave's Jewel in brass, as he advises elsewhere in the text?
Wherefore for your mater if you will haue your Iewel in mettall and take no great paines in working, … get faire new lattyn brasse somewhat thicke for it is a great fault if your Iewel be too light in taking altitudes, because euery small winde will stirre him and other causes also.Footnote 24
It turns out we have a means of answering this question quite definitely, because an example of Blagrave's Jewel was made in brass by the master craftsman Charles Whitwell in 1595. Gerard Turner has provided a close examination of Whitwell's Jewel, noting in particular the complexities of creating the fretted rete (i.e. the complex circular part, with star-pointers in the lower half and a grid in the top half, rotated to about 35º in Figure 1): ‘It is clear that Whitwell had trouble making this instrument. Cutting the fretwork must have been exceedingly difficult; several bars were miss-cut and needed repair.’Footnote 25 Turner concludes his analysis by stating that ‘Blagrave's design was, in fact, unrealizable’. Even Whitwell's instrument remained unfinished, and is one of only two known examples of the Jewel made in a material other than paper.Footnote 26 Whitwell was perhaps the finest craftsman of his generation: he was trained by the map-engraver and instrument-maker Augustin Ryther, himself a skilled artisan who made a wide range of instruments, only a handful of which survive. Whitwell's output has fared better: some twenty-six instruments survive, including finely crafted astronomical compendia, the earliest surviving English globe, and a group of seven instruments taken to Italy by the nobleman Robert Dudley in 1606.Footnote 27
Further evidence that Blagrave's Jewel was only even attempted in metal by trained artisans comes from an unusual source: an annotation to the title page of Gabriel Harvey's copy of the book. Harvey, a scholar, poet, courtier and controversialist, is well known as a copious annotator of his books, and the marks he made have been analysed in terms of their social as well as their personal meaning.Footnote 28 On the title page of Harvey's copy of Blagrave he has made a revealing comment: ‘The Instrument itself, made & sold by M. Kynvin, of London, neere Powles. A fine workman, & mie kinde friend: first commended unto me bie M. Digges, & M. Blagrave himself.’Footnote 29 So Blagrave himself advised Harvey to go to James Kynvyn, who may well have fared no better than Whitwell in constructing the Jewel (not to mention that there are no surviving examples by Kynvyn).
Two other sources of evidence for the difficulty of making Blagrave's Jewel are to be found in the other published descriptions of the instrument, first the abbreviated version printed as part of Thomas Blundeville's Exercises in 1594, and then the 1658 edition of Blagrave's text, which contains substantial editorializing by the astronomer John Palmer. Blundeville omits all mention of the physical construction of the astrolabe, and does not advise his readers to attempt to make their own, instead offering a ‘description’ of the instrument, i.e. its lines and parts, and then a series of uses.Footnote 30 Palmer, more than half a century later, notes that the ‘Artificer’ Matthew Hill of Bedford ‘did cut out two of [the Jewel's] Reets so exactly and truely, as I think the like hath not been done in Metall before’.Footnote 31 Even with the grain of salt that should accompany this statement, it indicates that long after instrument-making was established in England the rete of the Jewel was considered a difficult work to execute, believed by Palmer never to have been undertaken even around the time Blagrave was writing.Footnote 32
Given what we know about the manufacture of instruments, we can also remark on what is not included in Blagrave’s text. The most obvious omission in Blagrave’s work (and indeed all other instrument books) is any information regarding the sourcing, preparation and working qualities of brass, which was the principal material used in instrument-making. True, a number of publications on the Continent in the sixteenth century explained some of the process of making brass, but these are not referred to in instrument manuals and there is no evidence that they were known to mathematical practitioners; the earliest sustained account in English was published in 1662. None of this marks out Blagrave's Jewel as atypical. Pamela Smith has explored the general case of ‘how-to’ books in the early modern period, concluding that in the vast quantity of cases, practice was not possible on the basis of reading alone.Footnote 33 What, then, was the purpose of including instructions for making the Jewel? Here we have to distinguish between Blagrave's (or any author's) own intentions, the community that worked to bring books to print, and the uses to which books were put.
To take Blagrave himself first: like others who turned to print in order to advance themselves in a novel pursuit in the early modern period, Blagrave alludes to recent setbacks in his prefatory addresses.Footnote 34 The details are not relevant, but clearly for Blagrave becoming an authority on practical mathematics was intended to address straitened circumstances and personal misfortune. We get a little closer to the specifics of making if we consider the dedicatee of Blagrave's Jewel, William Cecil (Lord Burghley), who was one of the most important members of the Elizabethan court and well known as an enthusiastic supporter of practical mathematics.Footnote 35 In light of Cecil's approval of the use of instruments, especially in surveying and navigation, and his eagerness to advance the manufacture of useful devices, Blagrave was wise to position himself as someone who could explain and promote the making of (apparently) new instruments that would perform both practical and pedagogical feats. Revealing trade secrets was a part of many addresses to noble patrons, and sure enough Blagrave describes and illustrates a device to perform the most difficult of all engraving tasks: the delineation of extremely shallow curves.Footnote 36 Eric Ash has drawn attention to the way in which the minor gentry attempted to position themselves as uniquely placed to mediate between artisans and the patrons of private and state projects, and a book like The Mathematical Jewel was intended to serve just this kind of end.Footnote 37
Inside the workshop
Moving beyond authorial intention, to context and reception, we can gain a fuller picture of the significance of Blagrave's book and its instructions for making the Jewel. Recall that Blagrave's Jewel was published in 1585. It was in that decade that mathematical instruments were first offered for sale in shops near St Paul's (Humfrey Cole, James Kynvyn), the Royal Exchange (John Bull), Hosier Lane (John Reade, Christopher Paine), Dowgate (James Lockerson), Tower Hill (John Reynolds) and Leadenhall (Augustin Ryther).Footnote 38 This impressive coverage of all major areas of the City of London had occurred quite suddenly, with only two identifiable instrument-makers practising in London a generation before (Cole and, prior to him, Thomas Gemini). Blagrave was clearly participating in this period of rapid change in the market for instruments. Aside from his dedicatee William Cecil, Gabriel Harvey can be imagined as Blagrave's ideal reader. We can see from Harvey's annotations that he attended closely to the text, though his interest was really in the world of craft to which the book could act as a key. Like many of his contemporaries, Harvey was keen to extract information from mathematical books, and to become conversant in the language of practical learning – though not perhaps in the complexities of mathematical practice itself.Footnote 39
But it is all too easy to forget that the instrument-makers themselves constituted an audience for new texts. There is no reason to doubt, for instance, that Whitwell worked from Blagrave's instructions in The Mathematical Jewel. This idea takes us inside the workshop, and relates to the second sense of making that I wish to describe: the intertextuality of craftsmanship within the trade.
It is becoming increasingly clear that books, manuscripts and images served as models for artisans seeking new designs of instrument, either to offer in the name of the inventor or to appropriate as their own. Examples are not hard to find. Humfrey Cole and others borrowed from published calendars and latitude tables.Footnote 40 Images, too, served as templates. As Samuel Gessner has shown, texts and images played an important role in the renowned Arsenius workshop at Louvain, with the scholar Gemma Frisius acting as intermediary between scholarly and artisanal spaces.Footnote 41 In London, two nautical hemispheres, made by Humfrey Cole and Charles Whitwell, can be identified with specific texts and images: Martin Cortes's Breve Compendio de la Sphera y de la Arte Navegar, which appeared in English with the title The Arte of Navigation in 1561 and again in 1572, and Michel Coignet's Nieuwe Onderwijsinghe op de principaelste Puncten der Zeeuaert (New Instructions on the Principal Points of Navigation) (1580).Footnote 42
Instrument-makers’ workshops were spaces filled with tools and wood and metal – and also paper. Manuscript descriptions of instruments circulated widely, as did records of instruments printed directly from the finished product. There are now around twenty examples of these ‘reverse-printed’ paper instruments in existence, almost all dating from the middle of the seventeenth century and associated with the workshop of Elias Allen and his craft descendants (Figure 2).Footnote 43 Allen's shop at St Clement's was a clearing house of information and a rich source of books and manuscripts.Footnote 44 By the middle of the seventeenth century numerous go-betweens took over the role of mediating between instrument-makers, printers and scholars. Samuel Hartlib, John Pell and John Collins, for example, collected up documents relating to instruments in order to form a kind of storehouse of devices that could measure any quantity, calculate any figure and enhance any sense.Footnote 45 The large number of practical treatises and instrument books listed in William London's 1657 Catalogue of the Most Vendible Books in England is merely the public record, as it were, of a whole world of paper tools, descriptions and documents that facilitated the success and perpetuation of a bustling trade in instruments.Footnote 46
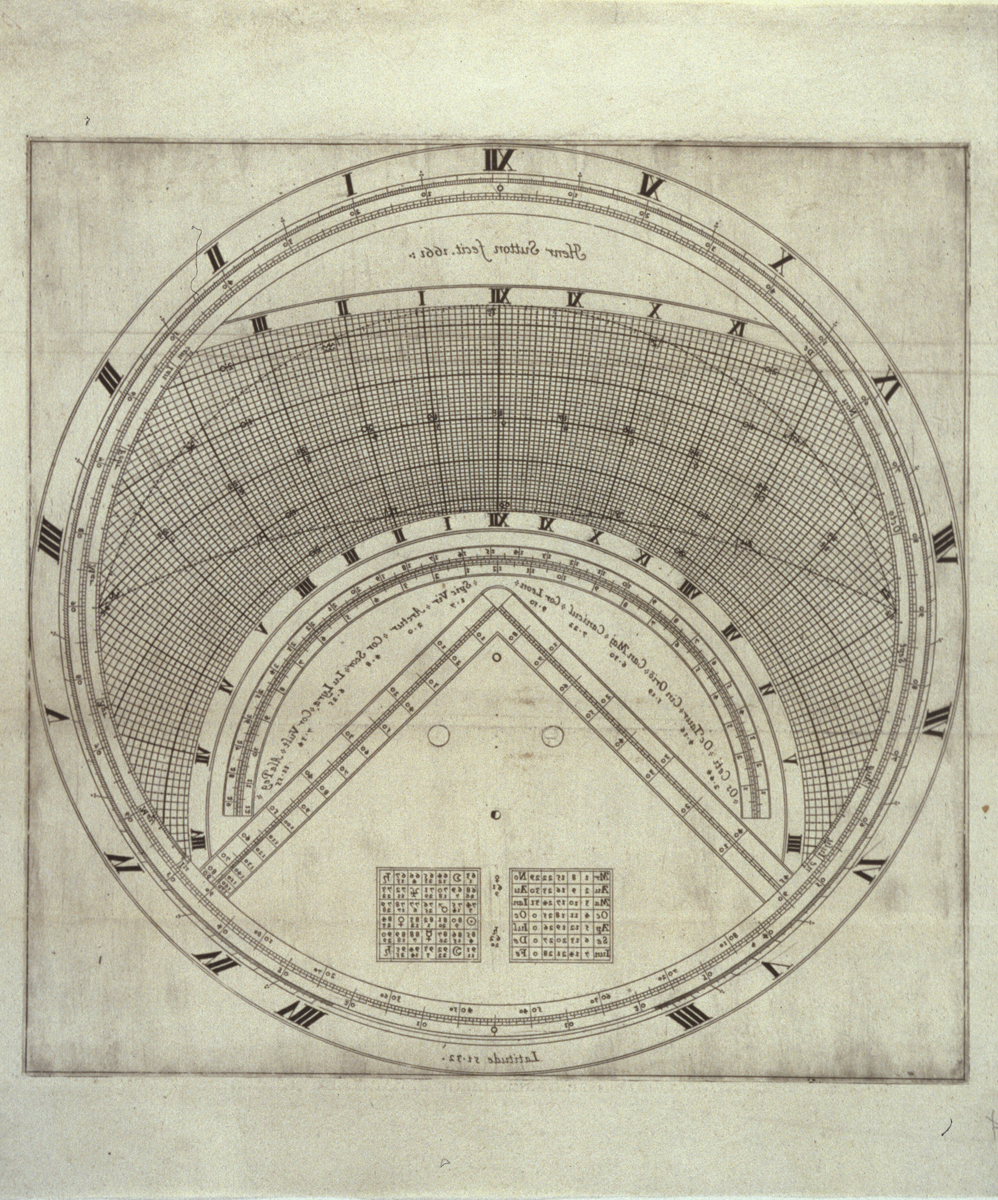
Figure 2. Printed horizontal instrument by Henry Sutton. The instrument is latitude-specific, and the outer circle represents the viewer's horizon (hence the name). The section engraved with celestial coordinates is bounded by the Tropics of Cancer and Capricorn, and shows the apparent path of the sun throughout the year. Note that this example has been ‘reverse printed’ from an instrument (rather than from a printing plate). A single counterproof could have been pulled from this print, making a working paper instrument. See Boris Jardine, ‘Reverse-printed paper instruments’, Bulletin of the Scientific Instrument Society (2016) 128, pp. 36–42, for this practice. Reproduced by permission of the British Library (MS add.4473.f10).
By attending to social and economic context it is possible to understand invocations to craft in instrument books as at once a rhetorical and a deeply practical move. This is to appeal to gentleman practitioners on the one hand and artisans on the other. Through the first half of the seventeenth century, other audiences opened up for authors with knowledge of new devices and techniques. The circulation of paper within the instrument trade has its parallel in the circulation of paper instruments amongst self-taught and commercially instructed surveyors, notaries, architects, scholars, gunners, customs officials, clerks and sailors. For these new readerships the role of making in textbooks meant something different. Alongside practical instruction in the use of wooden and brass instruments there was a world of practice that could be explored on and with paper. Here instrument books become truly hybrid, holding between their covers both the cognitive and the practical – just as far as the latter could go without requiring actual observation or use in the field. This was the kind of practice that could certainly be done by those without access to or knowledge of more recalcitrant materials, and although the evidence for paper practice is often subtle, it becomes more obvious the more we look for it.
Paper instruments
We have already seen one dramatic instance of a fully functioning paper tool in the pages of an instrument book: Blagrave's Jewel itself. There were few tasks that could be carried out with Blagrave's Jewel that were not catered for in the paper and pasteboard version that could be constructed by anyone with a knife and some patience for fine cutting. If we accept this much, it is only a short step to observing that a vast amount of mathematical ‘practice’ was done through making with paper. This should hardly be surprising – after all, more examples of Blagrave's Jewel survive in paper than in brassFootnote 47 – and yet the implications are only recently becoming apparent.
The notion of using images in books as instruments was not original to Blagrave. Many early modern texts encourage mutilation of prints and books in the service of mathematical practice. As early as 1562, for instance, Leonard Digges suggests in his Prognostication euerlasting that the reader ‘may use’ an image of a quadrant, ‘adding a plumbmet [sic] and lyne, with sightes or otherwise’.Footnote 48 Likewise Edward Worsop, in his 1582 defence of geometrical techniques in land surveying, pointed out that the book itself could become a tool of the new methods:
Every figure in this treatise is drawen according to some Scale, therfore the having of scales and compasses, and applying them to those figures, will make the demonstrations, and proofes herin very easie to the readers thereof, though they understand little or nothing in Geometrie.Footnote 49
Another writer who encouraged readers to work with images was William Gilbert, who in his De Magnete suggests at a number of points that the diagrams in the book can be cut out and pasted onto board, to be used as working instruments or, perhaps more accurately, movable demonstrations of the principles expounded in the book.Footnote 50
The experimental approach to using paper was continued by John Wybard, who was amongst the first to propose the ‘cut-and-weigh’ technique, whereby areas could be calculated by drawing them on paper, cutting and weighing them and comparing the result with a sample of the same paper of a known area.Footnote 51 Robert Hooke took this even further, turning paper into an experimental medium, as Matthew Hunter has shown.Footnote 52 It is also well known that the Billingsley Euclid of 1570 included flaps that could be cut and glued to illustrated propositions relating to solid geometry. Susanne Karr Schmidt has now added numerous examples of what she aptly calls ‘interactive and sculptural printmaking’, in the fields of theology, anatomy and practical mathematics.Footnote 53 And Margaret Schotte has explored the large variety of paper instruments – including charts, tables and manuals – that were used in navigational training and practice.Footnote 54
Although working with paper was possible in a range of areas of practice, one stands out as being particularly amenable to this particular material, namely dialling – that is, the construction of sundials. This was, as Jim Bennett has shown, a far more diverse and creative activity than we might suppose.Footnote 55 In fact even Blagrave's Jewel might be thought of as primarily a dialling instrument, albeit one with an extremely wide range of functions. In England dialling was important as a point of entry to the expansive study of cosmography – a heterogeneous subject of study that could extend from local topography to the movement of the planets. But dialling in sixteenth- and seventeenth-century England had an even wider attraction than this: it was practical enough to appeal to the new kind of civic humanism fostered amongst the gentry, but far enough removed from questions of commerce and value to risk corrupting pious disinterest. As a way to connect ordered and constrained (i.e. mathematical) study with geographical location and the regulation of daily and annual events, dialling was a route to nothing less than the modernization of time itself.
I return below to the work that could be done within instrument books – but to make clear the extent to which dialling could be done on and with paper we need to look beyond the confines of the printed page. The practice of making manuscript paper dials was specifically advocated by Joseph Moxon in his 1679 English Globe:
But before we go further let me advise you (whensoever you make a Dial of consequence, of what kind soever it be) to describe it first on Paper, and thence to mark out the Lines on your real Plane, for thereby you will not only keep your said Plane neat, and more judiciously chuse the best place for the Center of your Dial, but (besides the several conveniences which practice will show you) the Lines themselves will be more exactly drawn, by reason you can manage your Paper draught as you please.Footnote 56
Confirming that this and other similar injunctions were followed, we have extensive surviving evidence of manuscript instrument books, often made by practitioners unknown from other sources.Footnote 57 One exception to the rule of historical obscurity is Mary Evelyn, wife of diarist and educational reformer John Evelyn, who undertook a broad humanist education at Paris, including elements of mathematical practice.Footnote 58 Amongst her papers at the British Library is a series of manuscript sundials.Footnote 59
Dialling was a sophisticated art in this period, imparting the basics of geometry and cosmography, and explaining time as a function of the latter.Footnote 60 In studying and making sundials Mary Evelyn was embarking upon a path that was also followed by other more famous mathematicians, including Isaac Newton, John Flamsteed and Christopher Wren; lesser-known figures like Mark Ridley; and scholars in other disciplines like Roger North.Footnote 61 For each of these, making sundials and experimenting with projective geometry served as a way in to practical mathematics that was at once enjoyable, useful, topographically specific and universal in its implications.
We can see the relation of dialling to other disciplines – and the way that instrument books were read and digested – by considering the case of Thomas Brush (active c.1650), a self-styled mathematical practitioner now only known through the paper legacy he left behind.Footnote 62 Brush describes himself and his purpose as follows at the beginning of one of his books:
I thought good to show what use there is for Arithmitick And Geomitrie in ye making of ground plots: without wch it cannot be rightly performed as may appeare in this book … performed by Tho: Brush. Gardener &c practtisioner in ye mathamaticks &c.Footnote 63
Following this, Brush gives some general cosmographical propositions and data, a mathematically derived plot for an ornamental garden, extensive notes on the making of sundials, the projection of the sphere, arithmetic (including the use of ‘Napier's bones’), an introduction to trigonometry, advice on gauging casks, and some basic solid geometry. The section on solid geometry is of interest because, following the Billingsley Euclid, Brush constructs some folding geometrical solids out of paper. Likewise in the section on dialling, Brush, like Evelyn, makes working sundials out of his diagrams by erecting paper gnomons. And in the sections on stereographic projection he copies diagrams from textbooks by pricking the intersections of lines through onto his notebook and then either connecting them together into reworked diagrams or simply working from the dots themselves.Footnote 64
To be sure, we are now a few steps removed from considering the instrument book as a printed commodity. However, these kinds of manuscript practice – including commonplacing and paper dialling – exist on a continuum with the printed page. For one thing, as Brush shows, diagrams in books could be transferred onto separate sheets or into commonplace books. For another, the kinds of three-dimensional practice outlined here could easily be incorporated into printed books. Finally, the idea of working with or on diagrams brings together both print and manuscript.
Here the evidence of practice is more subtle, and the connection with ‘making’ more complex. From the beginning, instrument books required their readers to possess certain craft skills: not metalworking or line engraving, but geometrical drawing and the use of the compass and rule.
Projection as paperwork
While it is clear how a fully assembled astrolabe like Blagrave's could function (even if the specific functions remain complex), it is less clear how ideas of craft, technique and pedagogy apply to flat diagrams drawn or worked on with pen, compass and rule. Here it is necessary to introduce concepts recently developed by Jim Bennett, Richard Kremer, and Stephen Johnston, having to do with the way that certain images or diagrams could function as working instruments – and, by extension, the way constructing those images or diagrams could serve a pedagogical purpose in its own right. Bennett has developed the idea of ‘theorics’ – ‘geometrical construction[s] intended to contain and generalize measurements across space or across time, often employ[ing] mathematical techniques close to those involved in instrumentation’.Footnote 65 Kremer offers the related category of ‘geometrical tools’, focusing on the ‘graphical elements that allow users to solve a discrete geometrical problem’ and thereby avoiding questions of theory/practice, knowing/doing.Footnote 66 Johnston, finally, uses the term ‘graphical practice’ to describe the way in which geometrical projections ‘provide a means not only of representing but of manipulating objects in three dimensions’, thus ‘blurring ... the boundaries between instrument and diagram’.Footnote 67
In order to explore how these concepts can be incorporated into my analysis of instrument books, it will pay to focus on one specific kind of diagram, and an obvious choice is the projection in two dimensions of the celestial sphere, as this is the technique involved in Blagrave's Jewel; it also plays an important role in, for example, Brush's manuscript, and in many seventeenth-century practical mathematics texts.Footnote 68
The primary use of projection was as a kind of universal cosmographical tool, which could preface and illustrate specific tasks of spherical trigonometry, time telling, solar calculation, astrology and cartography. The mathematical collector and erstwhile author John Pell, for instance, planned around 1630 a book on the use of the astronomical quadrant for which manuscript notes survive:
it will be very convenient in the beginning of every booke to set a projection of ye sphaer in plano, representing ye particular latitude with every 5th parallel of Declination & every horary circle of <ye> Horizon or limb divided <actually> into 360 gr: which will very much help us <phansy> in conceiving ye reason of ye inequality of ye numbers in ye following tables.Footnote 69
Later writers concurred. John Aubrey, for example, conceived of a scheme (completed 1683/4) for the education of the young that included extensive mathematical training, and contained the following note: ‘Stoffler's astrolabe [a form of latitude-specific stereographic projection]. Every youth should have this in little in paper to teach him to erect a Scheme presently: wch will much delight & incourage them’.Footnote 70 And, likewise, William Leybourn's 1669 Art of Dialling proposes to teach the construction of sundials ‘geometrically’, ‘arithmetically’ and ‘instrumentally’: ‘The Geometrical Part whereof is performed by Projecting of the Sphere in Plano, upon the Plain itself, whereby not onely the Making, but the Reason also of Dials is discovered.’Footnote 71 The significance was practical and cognitive, with some authors emphasizing the former, and some the latter. One particularly striking example of this contrast is given in the competing books on the horizontal (latitude-specific) projection by William Oughtred and Richard Delamain. These two authors were engaged, in the early 1630s, in a priority dispute, in the context of which Oughtred articulated his own philosophy of mathematical learning – which emphasized sound theoretical grounding first and foremost – and attacked Delamain for making his own pupils ‘only doers of tricks, and as it were Juglers’ through over-reliance on instruments.Footnote 72 Although the dispute is relatively well known, the textbooks within which the controversy was conducted have attracted little attention, and in fact in their instructions for making paper horizontal instruments (i.e. astronomical calculating devices carrying a stereographic projection) the differences between the two teachers emerge in an unexpected way (see Figure 2).
Oughtred, in his first ‘use’ of the horizontal instrument, writes that it is possible ‘by the eye, and view only, to behold and comprehend the course of the Sunne, both for his Annuall and Diurnall motion’.Footnote 73 From the beginning of his treatment of the horizontal instrument Oughtred favours a visual/cognitive model of learning over a practical/constructive one. This is emphasized further when Oughtred comes to explain how to make a reusable paper version of the horizontal instrument:
The vse of this instrument on paper is, that lines, and arches may bee designed vpon it with a fine pennicell of blacke lead, and afterward be wiped out againe. Wherefore it will bee needfull for him that will vse this instrument, to all the purposes thereof, to get a good paire of large compasses with three points, one sharpe, another for inke, a third for blacke Lead. And I suppose it would doe well to fasten over your instrument a peice of thinne oyled paper, through which the lineaments may be conspicuous: and vpon it to trace such lines, and arches as you haue occasion to vse: that so your instrument may be kept cleane, and last longer.Footnote 74
Learning through projection is a matter of seeing and of copying, rather than of geometrical construction. Delamain, by contrast, begins with the construction of the horizontal instrument.Footnote 75 For this purpose Delamain includes a large folding sheet showing most of the construction lines that go into the making of the horizontal projection. For Delamain, teaching is done through making, and making takes place on paper.
Oughtred treats the projection as an illustration, with calculations performed on it only adding to this illustrative function. Delamain understands making itself to be a part of pedagogy, and encourages the construction of the diagram rather than its direct transfer. In this respect at least, Delamain appears to be offering a more rigorous and certainly a more difficult route to practice to his readers. While Oughtred's text meets the definitions of ‘theoric’ and ‘practique discipline’ very well, and ‘geometrical tool’ passably, it is not quite clear how we should categorize Delamain's instructions. Certainly imaginative work is being done, but the problems being solved are those of geometrical construction – as Delamain makes clear in his text, he expects his students and readers to learn through the construction of instruments. This is clearly a form of ‘graphical practice’, in which a particular technique of drawing is being taught. With the tools of the rule, compass and pen, the student of Delamain’s book will gain skills that can be carried over to a wide range of ‘mathematical arts’.
But graphical practice is not just a matter of drawing. It is also a way of approaching and working with and on diagrams themselves. This takes us back within the pages of the printed book, and back to the role of construction in pedagogy. In a copy of Gunter's Works held at Cambridge University Library, for example, another kind of universal projection has been extensively worked on, most likely using a tool known as a ‘blind stylus’, which incises paper without leaving an obvious mark (Figure 3).

Figure 3. Photograph in raking light showing extensive ‘blind-stylus’ work on an astronomical diagram in Edmund Gunter's Works (1673 edition). The blind stylus was a tool of artists and mathematical practitioners to score the page without leaving an obviously visible mark. Another technique was to oil the paper, creating a wipe-clean surface, or to prick through the diagram with a pin and trace the image onto a separate sheet. Cambridge University Library CCD.13.23. By permission of the Syndics of Cambridge University Library.
Here calculations have been carried out, and the diagram has been adjusted for a different latitude, as can be seen from the faint dotted lines. Possibly the lines have also been traced and transferred to another sheet of paper. This is perhaps the most literal sense in which mathematical practice could be conducted within an instrument book. Diagrams could be worked on with the stylus, or annotated directly. To give an example of the kind of calculation that could be carried out like this, here is Gunter's account of how to calculate the time and solar azimuth from a measurement of the sun’s altitude:
If the altitude of the Sunne be given, let a line be drawne from it parallell [sic] to the horizon; so it shall cross the parallell of the Sunne, and there shew both the azimuth and the houre of the day.Footnote 76
This ‘line’ is not necessarily an inscribed line, but an idealized one that could be brought into being by means of a ruler, piece of string or blind stylus. The lesson is a basic one leading to further propositions in astronomy, cosmography, navigation, horology and, ultimately, spherical trigonometry. It is now possible to see that ‘learning by doing’ was one of the main purposes of instrument books, and that this could happen on paper, either as well as or as a replacement for other kinds of manufacture. The case study of projection has revealed that in fact the range of kinds of practice was extensive, extending from the strictly illustrative to the strictly geometrical, via the practical.
Conclusion
The 1658 reissue of Blagrave's Mathematical Jewel – edited by John Palmer and published by Joseph Moxon – features an unusual frontispiece, which captures many of the themes discussed in this paper (Figure 4). In addition to being hybrid objects, instrument books created another kind of hybridity: the reader/user, who by ‘making’ on paper acquired knowledge that was at once theoretical and practical. In the frontispiece, note the conceit of the title displayed on a schoolroom teaching aid: the setting is undoubtedly scholarly, and the instrument's user is working through the propositions in (presumably) the book itself. This specific pose, with head resting in hand, was used in the period to indicate Melancholia, in the ‘inspired’ sense famously depicted in Albrecht Dürer's engraving of that title – an appropriate figure for our purposes.Footnote 77 The melancholic was understood to be in touch with ‘earthly’ things, in this case the practices understood to follow from learning to use the Jewel – but far from being ‘melancholy’ in our modern sense, mastery of these subjects was to lead to great moments of inspiration when the imagination, reason and intellect acted upon what was learnt through practice. Recalling the dialling manuscripts of Mary Evelyn mentioned above, we should also take the image literally, as a depiction of a young woman learning cosmography through the use of the projection.

Figure 4. Engraved frontispiece to The Catholique Planispaer, which Mr Blagrave calleth the Mathematical Jewel (London, Joseph Moxon, 1658). The portraits are of John Blagrave (left) and John Palmer (right), who edited and added to the text. The engraving is by David Loggan. © The Trustees of the British Museum.
Projections of the sphere functioned both as the basis of comprehension for a range of other tasks and techniques, and as end in themselves – this is why they were favoured in books on subjects as diverse as navigation, gunnery, surveying and (of course) astronomy. The great benefit of projection was that it could be done on paper, either from scratch or by copying. The emerging trope of using a projection as a frontispiece or a plate that could fold out and be visible while reading lies behind the thinking of the owner of Blagrave's book who mounted the assembled instrument inside its front cover (see Figure 1), thus creating a hybrid instrument/book.Footnote 78
Acknowledgements
This paper builds on work undertaken at Cambridge University Library during my tenure as Munby Fellow in Bibliography (2014–15); I am grateful to the staff at the UL for their generous support before, during and since.







