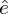Introduction
While the ecological impact of diffuse anthropogenic factors has been long recognised in ecosystem ecology (e.g. Crowe et al. Reference Crowe, Thompson, Bray and Hawkins2000), it is only comparatively recently that population conservation issues were explicitly looked at from this point of view. A number of human activities impact on animal populations at rates that are so low or in ways that are so indirect that they have for a long time implicitly been considered as innocuous or sustainable, often even going unnoticed. In fact, the impact is often translated as a rate relative to the human activity concerned, while the correct reference is the target size, i.e. the animal population.
The incidental bycatch of seabirds by fishing devices is one of the most striking examples and is seen as a major threat to some species, especially albatrosses (Croxall et al. Reference Croxall, Butchart, Lascelles, Stattersfield, Sullivan, Symes and Taylor2012) although information about the population level effect is lacking. For longline fishing, the rate of bird capture per hook is quite low, often as low as one bird caught per 50,000 to 200,000 hooks set (e.g. Gilman et al. Reference Gilman, Boggs and Brothers2003, Lewison and Crowder Reference Lewison and Crowder2003) although values up to 0.5 to 1 bird per 1,000 hooks set have been recorded (Ryan et al. Reference Ryan, Keith and Kroese2002, Lewison and Crowder Reference Lewison and Crowder2003). Such low rates give at first sight a feeling of innocuousness. However, the development of longline fisheries has led in some oceans to several million hooks being set every day (Lewison and Crowder Reference Lewison and Crowder2003). The absolute numbers caught resulting from the combination of a low rate per hook set and a huge number of hooks set are far from negligible, with estimates reaching 25,000 birds per year in the Laysan Albatross Phoebastria immutabilis in the late 1980s (Naughton et al. Reference Naughton, Romano and Zimmerman2007), and probably more than 300,000 seabirds per year at a global scale (Anderson et al. Reference Anderson, Small, Croxall, Dunn, Sullivan, Yates and Black2011). Soon after the first concerns emerged, various approaches provided evidence of a strong impact on some populations, in particular of albatrosses (e.g. Brothers Reference Brothers1991, Weimerskirch et al. Reference Weimerskirch, Brothers and Jouventin1997).
Deciphering the effects of longline fishery bycatch on seabirds has been the subject of intense activity over the last 20 years, from analysing bird behaviour to assessing the consequences on populations (see e.g. Lewison et al. Reference Lewison, Crowder, Read and Freeman2004, Arnold et al. Reference Arnold, Brault and Croxall2006), from estimating of the numbers caught by various types of fishing activities (synthesised by Anderson et al. Reference Anderson, Small, Croxall, Dunn, Sullivan, Yates and Black2011) to developing and assessing the effectiveness of various mitigation measures (Brothers et al. Reference Brothers, Gales and Reid1999, Gilman et al. Reference Gilman, Boggs and Brothers2003).
After early studies that discussed the estimated bycatch relative to the estimated population size, usually expressed as a number of breeding pairs (e.g. Ryan et al. Reference Ryan, Keith and Kroese2002), investigations of population level consequences became rapidly more and more sophisticated. The degree of sustainability of the estimated bycatch levels was approached with the help of population projection models (Weimerskirch et al. Reference Weimerskirch, Brothers and Jouventin1997, Lewison and Crowder Reference Lewison and Crowder2003, Arnold et al. Reference Arnold, Brault and Croxall2006,). Capture-mark-recapture (CMR) analyses went one step further by providing evidence for a drop in survival in correlation with bycatch (Weimerskirch et al. Reference Weimerskirch, Brothers and Jouventin1997).
In fact, even at a low rate, albatrosses are literally fished, and the population problem is thus an exploited population problem, even if exploitation is incidental. Considering the problem of seabird bycatch, as well as other conservation issues (Reynolds et al. Reference Reynolds, Mace, Redford and Robinson2001), as an exploited population problem brings decisive advantages (Lebreton Reference Lebreton2005). First, the theory of exploited populations, e.g. with measures of Catch per Unit of Effort (CPUE) (Haddon Reference Haddon2001) relates the effect of exploitation to its intensity. Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) used such an approach to show that survival in the Black-footed Albatross Phoebastria nigripes (hereafter BFAL) was directly related to covariates reflecting the intensity of fishing activity. Second, the theory of exploited populations (TEP) also predicts that survival should decrease in an approximately linear fashion with the proportion exploited (for a review see Lebreton Reference Lebreton2005). This prediction has been used in the context of conservation and management of animal species for quarry species such as ducks (Anderson and Burnham Reference Anderson and Burnham1976, Nichols Reference Nichols, Perrins, Lebreton and Hirons1991) and geese (Gauthier et al. Reference Gauthier, Pradel, Menu and Lebreton2001). The various estimates of bycatch available for seabirds have never been used to directly model and predict the change induced on survival, although doing so would bring direct evidence for the effect of bycatch, help assess its biological significance, and thus improve our ability to decipher the complexities of this low rate exploitation.
The purpose of this paper is to relate survival in the BFAL with annual estimates of total bycatch made available by Naughton et al. (Reference Naughton, Romano and Zimmerman2007). We use modern capture-recapture methodology, taking advantage of the detailed investigation by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007), simply using a CMR model with a built-in linear regression (Lebreton et al. Reference Lebreton, Burnham, Clobert and Anderson1992) constraining the survival probability to be a linear function of the estimated bycatch.
We take into account and discuss the unavoidable uncertainties and biases in bycatch estimates. On the one hand, the uncertainties in the covariate tend, as in all regression models, to bias the slope toward 0 (Barker et al. Reference Barker, Fletcher and Scofield2002), in an “error-in variable” problem. On the other hand, bycatch estimates tend without any doubt to be underestimated (Brothers et al. Reference Brothers, Gales and Reid1999, Brothers Reference Brothers2008, Anderson et al. Reference Anderson, Small, Croxall, Dunn, Sullivan, Yates and Black2011). First, various direct biases in the survey of birds hauled on board exist (Brothers Reference Brothers2008); second, the number really caught should include birds killed by the line but not hauled on board, named for short “drop-off”, that may reach 50% of the total kill (Brothers Reference Brothers2008, Brothers et al. Reference Brothers, Duckworth, Safina and Gilman2011). The latter part is the exact equivalent of the crippling loss of quarry species, consisting of animals killed by hunting activity but not retrieved by hunters, and thus not included in hunting bag surveys (e.g. Van Dyke Reference Van Dyke1981). Finally, the extrapolation to obtain overall figures is inherently fragile, as this extrapolation inevitably encompasses fleets submitted to looser regulations than those having accepted observers on board (Anderson et al. Reference Anderson, Small, Croxall, Dunn, Sullivan, Yates and Black2011). We develop predictions on the effect of these various uncertainties and biases after a description of the methods and data. We expect, by using a more directly functional covariate and a wider time window than Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007), to obtain stronger evidence for a bycatch-survival relationship in the BFAL, and more broadly, to contribute to the toolbox for understanding the effects of diffuse man-induced mortality in animal populations.
Material and methods
Data
The Black-Footed Albatross is a near-endemic of the Hawaiian archipelago. Concerns for this rare species (around 60,000 breeding pairs) have been reviewed by Cousins and Cooper (Reference Cousins and Cooper2000) and Naughton et al. (Reference Naughton, Romano and Zimmerman2007). The species is classified as “Endangered” by IUCN. We use CMR data already used by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007). The data consist of individual histories of 13,854 BFAL banded as chicks on Tern island from 1980 to 2004, and recaptured as breeders from 1997 to 2004 (see Véran et al. Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007 for further details).
Capture-recapture analysis
The data were analysed using multistate capture-recapture recruitment models (see e.g. Lebreton et al. Reference Lebreton, Hines, Pradel, Nichols and Spendelow2003), with two states, ‘Breeder’ and ‘Non-Breeder’. Individuals were marked as chicks in the ‘Non-Breeder’ state. The transition from ‘Non Breeder’ to ‘Breeder’ started at age 5. Individuals were never re-observed as Non-Breeders, i.e. the state Non-Breeder was not observable. Various constraints in relation to goodness-of-fit, parameter identifiability, and biologically relevant questions were considered, leading to several different models that were all fitted using E-Surge (Choquet et al. Reference Choquet, Rouan, Pradel, Thomson, Cooch and Conroy2009a).
The goodness-of-fit of an initial model was assessed based on the adult part of the CMR histories (i.e. reduced to breeders, following Crespin et al. Reference Crespin, Harris, Lebreton, Frederiksen and Wanless2006, Lebreton et al. Reference Lebreton, Nichols, Barker, Pradel and Spendelow2009), using program U-CARE (Choquet et al. Reference Choquet, Lebreton, Gimenez, Reboulet and Pradel2009b). Following Crespin et al. (Reference Crespin, Harris, Lebreton, Frederiksen and Wanless2006), the initial model considered time and age dependence in recruitment (with stabilisation at age 10, i.e. nearly all the information up to the first recapture as a breeder was used in this model to estimate recruitment), time dependence and two age classes for survival.
An estimate of an overdispersion coefficient reflecting heterogeneity in the data was derived from the goodness-of-fit statistics.
The basic parameters in our models were:
∙ First year survival probability
∙ After-first year survival probability
∙ Age-specific probabilities of transition from Non-Breeder to Breeder (at ages 5, 6, and 7+); the constancy of the recruitment probability from age 7 onwards together with the assumption of the same survival for breeders and non breeders of the same age are sufficient to ensure the statistical identifiability of all parameters (Gimenez et al. Reference Gimenez, Choquet and Lebreton2003, Lebreton et al. Reference Lebreton, Hines, Pradel, Nichols and Spendelow2003).
∙ Probabilities of recapture of breeders, that were non null only for occasions 17 to 25, i.e. years 1997 to 2004 (as all recaptures took place from November to January, these calendar years are those of the corresponding November and December months).
As there were no recaptures of marked individuals between the chick stage and age 5, only a compound immature survival probability from the chick stage to age 5 could indeed be estimated. As a first approximation, we assumed that survival probability was independent of age from age 1 onwards, whether the bird was a breeder or not. As this after-first year survival probability could be estimated from recaptures of breeders, one could in turn derive from the compound immature survival probability an estimate of the probability of survival from the chick stage to age 1. As this first year survival probability was estimated in an indirect fashion and concerned birds that were at sea for less than a full year, we expected it to be less sensitive to bycatch than the after-first year survival probability.
Bycatch as a covariate
According to TEP, when a proportion h of a population or a population subset such as a particular age-class with baseline survival probability S 0 is harvested, the probability of survival should approximately vary as S = S 0(1 − h) unless there is some form of compensation, that may lead to S = S 0(1 − bh) with b < 1 (see review in Lebreton Reference Lebreton2005).
Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) started from this basic relationship and investigated the relationship between survival probabilities and covariates reflecting fishing effort F, to which h is presumably proportional, as h = gF, leading thus to S = S 0(1 − gF). To protect the regression against the use of too many variables that would have biased statistical tests, they first reduced eight fishing effort covariates to three principal components, and then showed that the survival probability of adult albatross was significantly related to the second principal component (PC2), with a test level corrected for multiple testing.
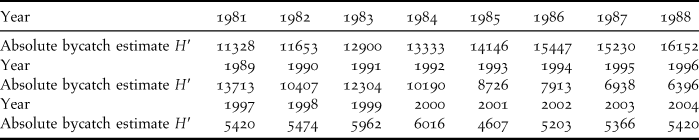
We here take advantage of the recent availability of annual estimates of the total BFAL bycatch (Figure 4 in Naughton et al. Reference Naughton, Romano and Zimmerman2007). We sampled their figure to obtain the values in Table 1 and we used these values as a covariate to model survival probabilities.
Our analysis differs from that of Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) in the following respects:
1) Thanks to the availability of the bycatch estimate we were able to use more data over more years. We used a recruitment model with 13,854 individuals from ringing as a chick to recaptures as breeders over 25 years (1980–2004) while Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) used the first capture as breeder as the initial marking and used 2,046 capture histories of breeders over the 12 years (1992–2003) for which measures of fishing effort were available.
2) As a side-effect, we were unable to use the sophisticated treatments of heterogeneity used by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) and we expect a higher overdispersion coefficient. The comparison between three types of models by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) shows that the estimates are not very sensitive to the treatment of heterogeneity. A higher overdispersion coefficient will induce a decrease in power, i.e. will be conservative relative to bycatch assessment.
3) Based on TEP, we will be able to discuss the slope value, as in the absence of bias and compensation it is expected to be equal to 1.
Table 1. Black-footed Albatross absolute bycatch estimates (denoted as H′) obtained by sampling Figure 4 of Naughton et al. (Reference Naughton, Romano and Zimmerman2007).
Predictions on the effect of bycatch
The absolute bycatch H can be converted into a relative estimate h by dividing H by an estimate of total population size N, as 
$h = {{$H$} /{$N$}}$. The ratio Population size / Number of breeding pairs in the BFAL is, as in all albatross species, close to 5 before the annual birth pulse (Cousins and Cooper Reference Cousins and Cooper2000), a value derived from the stable population structure in a matrix model. With an average population size near 60,000 pairs, we used N = 300,000. The effect of potential bias and uncertainties at this stage is discussed below.
Table 2. Initial multistate capture-recapture models for the Black-Footed Albatross data.
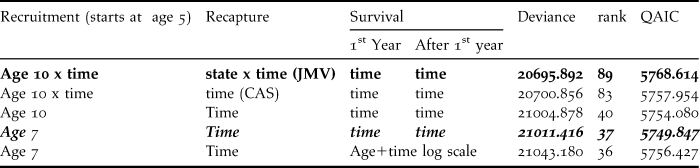
Recapture: JMV = Jolly-Move model with dependence of recapture probability on time x state of origin x state of arrival; CAS = Conditional Arnason Schwarz model with dependence of recapture probability on time x state of arrival reducing to time dependence as recaptures occur only in state “Breeder”. Recruitment: The age of stabilisation of the recruitment is given, with or without time effect depending on the model. The model in non-Italic bold is the umbrella model. Goodness-of-fit analysis of this provides an estimated overdispersion coefficient equal to 3.7019. Further analyses proceed from the model in Italic bold with minimal QAIC.
As mentioned earlier, one may ideally expect a slope b equal to 1 in S = S 0(1 − bh). It could be modified by compensation, a phenomenon of direct biological interest, and by various artefacts. While compensation is not expected to be strong in such a long-lived species (Gauthier et al. Reference Gauthier, Pradel, Menu and Lebreton2001, Lebreton Reference Lebreton2005), two main artefacts exist:
- Bias in N and H, the latter estimated as H′, inducing a bias in h. With a multiplicative expression of the bias, h′ = dh in which h is the true relative bycatch, the relationship S = S 0(1 − bh) = S 0(1 − b′h′) = S 0(1 −b′ dh) shows that the slope expected when using h′ = dh as a covariate, is
$b’ = {{b}/{d}}$. If the bycatch proportion is underestimated, i.e. d < 1, then b′ > b. The potential bias in h results first from underestimation of H by H′, a well known problem whose components are: drop-off, extrapolation to periods without observers on decks and to fleets without observers. Most experts (e.g. Brothers et al. Reference Brothers, Duckworth, Safina and Gilman2011, Moore and Zydelis Reference Moore and Zydelis2008) seem convinced each of these two main types of bias may be in the order of several times 10%. Hence, a value of d as low as 0.5 seems quite likely. The BFAL population at sea includes immature birds and is thus larger than that deduced from the number of breeding pairs, which estimates population size just before the annual birth pulse, i.e. after some mortality of these immature birds. Similarly the factor 5 retained for deriving an estimate of total population size N from the number of breeding pairs tends to underestimate total population size, compared with the value 6 proposed by Dillingham and Fletcher (Reference Dillingham and Fletcher2011). Our choices tend thus to increase the estimated relative bycatch h′ and are thus conservative relative to the sources of underestimation.- Uncertainty in h′, inducing an “error-in-variable’ problem resulting in an “attenuation” of the estimated slope towards 0. The estimated values H′ in Table 1, scaled down by a factor 10-5 have an estimated mean of 0.0975 and variance of 0.001435. In the figure of Naughton et al. (Reference Naughton, Romano and Zimmerman2007), these estimates come with confidence intervals that can be grossly converted into a coefficient of variation close to 20%. The sampling variance (still for rescaled values) can thus be grossly estimated as ς 2 ≈ 0.22 × 0.09752 = 0.000380. From var(H′) = var(H) + ς 2 = σ 2 + ς 2, and var(H′) ≈ 0.001435 we deduce σ 2 ≈ 0.001058. The error-in-variable issue is expected to “attenuate” the slope from 1 to
${{\sigma ^2 } \over {\sigma ^2 \,+\, \varsigma ^2 }} \approx 0.735$. The scaling of H′to h′ by dividing by an estimated population size and the sampling of H′ from Figure 3 in Naughton et al. (Reference Naughton, Romano and Zimmerman2007) potentially contribute also to the attenuation but were considered as second-order effects relative to the effect of uncertainty in the estimated absolute bycatch. For 1988, the only year for which a number is given by Naughton et al. (Reference Naughton, Romano and Zimmerman2007), our sampled value, 16,152, differs only by 0.4% from the actual one, 16,215. As all captures and recaptures took place between November and January, the use of calendar year bycatch estimates brings almost no further approximation or uncertainty.
For the sake of simplicity, we modelled the survival probabilities as functions of the estimated absolute bycatch H′, as S = S 0(1 − eH′), and converted to results relative to the estimated relative bycatch 
$h\prime = {{${H\prime }$} /{$N$}}$, as S 0(1
$\,- \,b’{{${H’}$}/{N}$), by using the relationship 
$\hat b’ = \hat eN$.
Results
There was strong evidence for heterogeneity with an overall goodness-of-fit statistic equal to 88.846, for 24 df. The various components gave the following ratios χ2/df: Test3.SR 27.777/6 = 4.63, Test3.SM 45.7534/9 = 5.08, Test2.CT: 14.8714/5 = 2.97, Test2.CL: 0.4441/4 = 0.11. We attribute the higher values for Test3 components to differences in recapture rates of new breeders and experienced ones as a result of the temporary emigration demonstrated by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007). We used for QAIC based model selection an overdispersion coefficient based on the overall statistic 
$\hat c = {{${88.246}$} /{${24}$}} = 3.7019$. As expected, this coefficient was higher than that obtained by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007), equal to 3.02 for a Cormack-Jolly-Seber survival model.
The first five models (Table 2) started from the initial model directly linked to the goodness-of-fit tests and explored a few reduced structures. We considered departure and arrival state dependence combined with time dependence for recapture probability, i.e. this starting point was for breeders the Jolly-Move (JMV) model (with rank = 89 for 169 parameters). The goodness-of-fit results above apply to this model as explained in the Methods section.
Applying the estimated overdispersion coefficient (
$\hat c$= 3.7019) lead to QAIC = 5768.614. The QAIC decreased when the capture probability was made dependent only on the arrival state, i.e. in the CAS counterpart of the umbrella model (QAIC = 5757.954), and when considering constancy over time in recruitment (QAIC = 5754.080). Recruitment rate could then be stabilised at age 7 (QAIC = 5749.847). This model was still clearly over-parameterised with 37 separately identifiable parameters only for a total of 59 parameters, as with few years of recapture all time-dependent survival probabilities cannot be separately estimated. As the effort in recapture was known to have varied over the years, no attempt was made to make the probability of recapture constant.
Hence, in relation to our main objective, further models (Table 3) examined various relevant structures for first year and after-first-year survival probabilities: time dependence, constancy, or linear dependence on estimated bycatch H′. While the model with constant survival did better than the time-dependent one, models with covariates did uniformly better than those with either constant or time-dependent survival. The model with different slopes for H′ for first year and after first year survival in the relation S = S 0(1 − eH′) reduced to the model with constant 1st year survival as the estimated slope for 1st year survival was 0, on the boundary of the admissible range. This model (QAIC = 5732.937) was preferable to the model with the same slope for first year and after first year survival (QAIC = 5733.437).
Table 3. Survival structure of the capture-recapture model for the Black-footed Albatross data. The absolute bycatch H′ is used to model survival probabilities according to the theory of exploited populations as S = S 0(1− b x H′)
The estimated bycatch H′ explained 59.9 % of the difference in deviance between the time dependent and constant models for after first year survival (under constant first year survival), a highly significant value (t(19) = 5.46, P = 1.4 10-5, one-tailed test accounting for overdispersion, Lebreton et al. Reference Lebreton, Choquet and Gimenez2011). The difference in deviance between the time-dependent model and the covariate model (21119.588-21073.588 = 45.495, for a difference of 33-14 = 19 in model rank) did not provide evidence for any unexplained variation in survival over time when compared to the overdispersion coefficient (F(19,24) = (45.595/19)/3.7019 = 0.6482, P = 0.831).
The estimate of the first year survival probability was 0.6536 ± 0.0512 (95 %CI: 0.5532, 0.7540). The estimate of the baseline after first year survival (S 0) was 0.9647 ± 0.0199 (95 % CI: 0.9258, 1.0036). The estimate of the slope of the after first year survival relative to the estimated absolute bycatch H′ was 1.14770 10-5 ± 0.24699 10-5 (95 % CI: 0. 64399 10-5, 1.65140 10-5). The estimated recruitment probabilities (Pr (Non Breeder → Breeder / age)) were as follows: age 5: 0.0216 ± 0.0064; age 6: 0.2904 ± 0.0255; age 7 and later: 0.5868 ± 0.0417. These estimates are quite sensible, with more than 95% of individuals (if alive) recruiting between ages 6 and 10, and comparable to recruitment patterns in other albatross species (e.g. Alderman et al. Reference Alderman, Gales, Tuck and Lebreton2011).
The baseline after 1st year survival, 0.9647 (± 0.0199) was quite comparable to those obtained in albatross populations considered as not submitted to bycatch (Véran et al. Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007; see also Alderman et al. Reference Alderman, Gales, Tuck and Lebreton2011). For the years 1997–2002, we obtained an average after-first-year survival equal to 0.904, reasonably comparable to the values 0.920 and 0.917 obtained by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) based on a model with an unobservable state to account for temporary emigration and a standard Cormack-Jolly-Seber model, respectively. The after-first-year estimated survival probability averaged over the 24 years, 0.858, is much lower as it covers the period with the higher estimated bycatch. It is 11.0% lower than the baseline survival. As all after-first-year age classes are concerned, this percentage translates into a percentage change on the population growth rate through the elasticity of the after-first year survival, 1-1/T (Lebreton and Clobert Reference Lebreton, Clobert, Perrins, Lebreton and Hirons1991), where T, the generation time is approximately equal to 25 (Cousins and Cooper Reference Cousins and Cooper2000). The resulting percent change is growth rate is 10.6%. The maximum growth rate of BFAL has been estimated to 1.059 by Niel and Lebreton (Reference Niel and Lebreton2005). Decreasing by 10.9 % the maximum growth rate of 1.059 proposed by Niel and Lebreton, one obtains fair evidence for decline, at an estimated rate slightly higher than 5% a year. Under the baseline survival probabilities, i.e. in the absence of bycatch, if each BFAL female were raising 0.8 chicks to fledging each year from age six onwards, the resulting growth rate would be 9.38% a year. Even in this optimistic and unrealistic scenario, the population would thus be unable to sustain the bycatch.
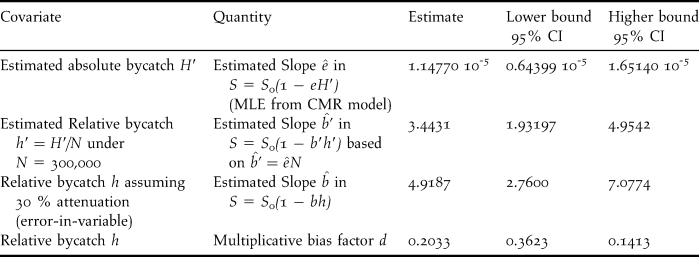
The estimated slope can then be analysed with respect to the theory of exploited population. To this effect, we converted the estimated slope 
$\hat e$ relative to the absolute bycatch H into an estimated slope 
$\hat b’$ relative to the estimated relative bycatch h′ using the conversion 
$\hat b’ = \hat eN$ (Table 4). The resulting slope estimate, 3.4431, seriously departs from 1, even more if accounting for the expected level of attenuation. Similar results were obtained under the second best model. The dominant source for such a difference can only be in the underestimation of bycatch, even if one might imagine a slight effect of heterogeneity. From the further calculations in Table 4, converting in a similar fashion the boundaries of the confidence interval of the estimated slope and exploring the effect of attenuation, it seems unavoidable to conclude that the bycatch estimate is underestimated by at least 50%.
Table 4. Estimated slopes of the linear relationship between survival and bycatch expressed in different fashions in the Black-Footed Albatross, from which one deduces minimal, “average” and maximal value of the multiplicative bias of bycatch. Even the value corresponding to the minimal bias, 0.4142, points to a strong underestimation of the bycatch, by at least 50%.
Discussion
Our study first confirms how critical is the bycatch problem for the BFAL, in two ways: first, a direct linear effect of bycatch on survival (explaining nearly 60% of the variation in after- first-year survival, a value certainly biased down by the uncertainty on the bycatch), second, a strong effect size. This strong effect size is apparent both in a strong drop in survival relative to the baseline survival, and a high slope estimate that provides fair evidence for a strong underestimation of bycatch. The slope value does not point to any form of compensation, as generally expected for long-lived species (Gauthier et al. Reference Gauthier, Pradel, Menu and Lebreton2001).
As there are few years of recapture, one should understand the relationship as follows:
For the years 1997–2004 (years 17 to 24), the drop in the after-first-year survival probability from a plausible baseline value around 0.96 to around 0.92 among 300,000 after-first year individuals at risk of by catch implies a bycatch around 0.04*300 000 = 12,000 individuals, while the mean estimated value is 5,555. Using a less conservative estimate of total population size would only tend to increase this figure, which by itself already points to the underestimation of the bycatch. The figure of 12,000 individuals exactly matches an early warning by E. Melvin (pers. comm. in Niel and Lebreton Reference Niel and Lebreton2005).
Then the rest of the data are, for the years prior to this period, characterised by high bycatch levels, compatible with even lower survival probabilities. The lack of evidence for a variation of first-year survival with bycatch estimate is easily explainable:
∙ The first year birds fledge around July (Cooper and Cousins Reference Cousins and Cooper2000) and are thus at risk for only six months;
∙ In a recruitment model such as ours, what is actually estimated is the survival from fledging to the age of first reproduction at the population level, i.e. five years. The first year survival is estimated indirectly by applying from age 2 to 5 the after-first-year survival estimated from older birds, in an assumption that cannot be tested. This parameterisation makes it possible to manipulate annual survival probabilities that can be related to annual bycatch through the TEP, but dilutes the potential effect of bycatch on first year survival.
The overall immature survival, and in our case the first year survival deduced from it, might also be modified by natal dispersal. However the high first year survival probability estimate rather points to strong philopatry, as is generally the case among albatrosses (Milot et al. Reference Milot, Weimerskirch and Bernatchez2008).
More broadly, our survival results are based on a few years of data and do not provide by themselves unequivocal evidence. However, a) the strength of the relationship, b) the robustness with respect to heterogeneity of the various models used by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) and in this paper, c) the sensible baseline survival estimates, and d) the similar average survival estimates in the last six years between our model and those by Véran et al. (Reference Véran, Gimenez, Flint, Kendall, Doherty and Lebreton2007) all make strong sense.
Our results match and confirm what is known or suspected for bycatch underestimation (Brothers Reference Brothers2008, Brothers et al. Reference Brothers, Duckworth, Safina and Gilman2011), as a result of the following biases:
1) The fleets on which observation can take place are likely the more ethical ones and a simple extrapolation may induce underestimation;
2) The observer not being continuously on deck; there is certainly some under-declaration when they are absent;
3) Drop-off and crippling loss of injured birds are not accounted for in these estimates as only birds hauled on board are counted. Brothers (Reference Brothers2008) and Brothers et al. (Reference Brothers, Duckworth, Safina and Gilman2011) estimate that only 50% of seabirds caught are hauled on board.
It seems thus that an underestimation by at least 50% should be the rule: our results bring independent confirmation for such an order of magnitude.
It seems that the strong effect of bycatch for which we got evidence did not translate into what is known of population size through monitoring of colonies, as the observed decline over the period 1990–2005 (Naughton et al. Reference Naughton, Romano and Zimmerman2007) has not reached a rate of 5% a year. Our results do not point to an imbalance of bycatch towards younger age classes, which could have explained a dampening of the bycatch effect at the population level. Delayed recruitment and a possible compensation in recruitment might explain the apparently limited impact on the number of breeders of the estimated change in survival. A more detailed assessment through a formal population projection model would be needed (see Véran and Lebreton Reference Véran and Lebreton2008).
Coming back to bycatch as a population exploitation problem, several authors (Wade Reference Wade1998, Niel and Lebreton Reference Niel and Lebreton2005) recommended including a safety margin when calculating sustainable bycatch. Our results on the underestimation of bycatch provide clear confirmation of the need for such a margin when assessing sustainability.
Finally, we wish to insist on the fact that the discussion on the underestimation of bycatch should not be taken as a criticism of the observation programmes that produce such estimates. On the contrary, it is clear that each piece in the puzzle suffers from its own shortcomings, but is essential in assembling a coherent image. We recommend that integrated monitoring programmes, combining marked individuals, bycatch assessment and population counts are developed to help produce a coherent image though integrative tools such as those brought by the theory of exploited populations.
Acknowledgements
This project was partly funded by Cooperative Agreement NA17RJ1230 between the Joint Institute for Marine and Atmospheric Research (JIMAR) and the National Oceanic and Atmospheric Administration (NOAA). The views expressed herein are those of the authors and do not necessarily reflect the views of NOAA of any of its subdivisions. We thank E. Flint and her colleagues at the US Fish and Wildlife Service, Honolulu, for providing access to invaluable data and continuing help. The field research was done on a National Wildlife Refuge by refuge staff and volunteers. We would like to thank the field workers for their hard work banding and reading bands. We thank two anonymous referees for helpful comments.
