Soit x1 ≤ x2, ≤ … ≤ xn—m + 1 ≤… ≤xn—p+1≤…≤ xn un échantillon ordonné de taille n d'une distribution dont F(x) et T(x) sont respectivement la fonction de répartition et la fonction de densité.

Nous appelons xn—m+1 la valeur de rang m de l'échantillon (x1, x2,…xn).

Pour simplifier l'écriture nous remplacerons partout l'indice n — m + I par m.

Avec cette convention nous notons la valeur caractéristique de rang m et l'intensité de rang m respectivement par um et αm [I].

Par définition on a:

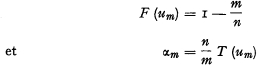
Notons enfin par Fm (x) et Tm (x) la fonction de répartition et la fonction de densité de xm pour n → ∞ et m fixe.

2.1. Avant de résumer les différents points traités dans cette note, rappelons les particularités qui caractérisent la distribution asymptotique de la plus grande valeur x1 d'un échantillon. On sait que cette distribution existe si et seulement si la fonction de répartition F(x) appartient à un des trois types suivants [2]:

a) Type I: F(x) est du type exponentiel.

Le domaine de x est illimité vers la droite et F(x) tend vers I pour x → + ∞ au moins aussi rapidement qu'une fonction exponentielle.

Tous les moments de F(x) existent.

b) Type II: F(x) est du type de Cauchy.

Le domaine de x est illiminté vers la droite.