Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T15:31:17.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Survival Probabilities Based on Pareto Claim Distributions

Published online by Cambridge University Press:  29 August 2014

Hilary L. Seal
Hilary L. Seal*
Affiliation:
Ecole Polytechnique Fédérale de Lausanne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is commonly thought that the characteristic function (Fourier transform) of the Pareto distribution has no known functional form (e.g. Seal, 1978, pp. 14, 40, 57). This is quite untrue. Nevertheless the characteristic function of the Pareto density is conspicuously absent from standard reference works even when the Pareto distribution itself receives substantial comment (e.g. Haight, 1961; Johnson and Kotz, 1970, Ch. 19; Patel, Kapadia and Owen, 1976, § 1. 5).

The Pareto density may be written

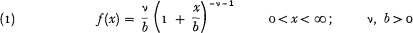
with distribution function

mean = p/(v − 1) and variance = b2v(v − 1)2(v−2). These are infinite when v≤1 and v≤2, respectively. Its Laplace transform (s= c + iu)

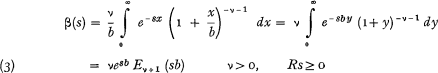
where E is the generalized exponential integral (Pagurova, 1961) and can be written in terms of incomplete gamma or confluent hypergeometric functions (Slater, 1960, Sec. 5.6). When s = − it β(s) becomes the characteristic function (see Appendix I).

As Benktander (1970) tells us, the Pareto distribution has been particularly successful at representing the distribution of the larger claim amounts. In earlier years it was employed to represent the distribution of life insurance sums assured but more recently it has been used for the claim distributions of fire and automobile insurance. Table 1 provides the v-values we have been able to locate. Note that the variance of the distribution is infinite when v≤2 and if it were not for the anomalous v-values of Andersson (1971) we would have ventured the opinion that modern claim data encourage the assumption that v>2. In our numerical work we have used v = 2.7 and smaller values might change some of the computer rules we have proposed in Appendix II.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 11 , Issue 1 , June 1980 , pp. 61 - 71
Copyright
Copyright © International Actuarial Association 1980

References

Ammeter, H. (1971). Grösstschaden-Verteilungen und ihre Anwendungen, Mitt. Verein. Schweiz. Versich.-Mathr. 71, 35–62.Google Scholar
Andersson, H. (1971). An Analysis of the Development of the Fire Losses in the Northern Countries after the Second World War, Astin Bull., 6, 25–30.CrossRefGoogle Scholar
Benckert, L. G. and Sternberg, I. (1957). An Attempt to find an Expression for the Distribution of Fire Damage Amount, Trans. XV Int. Cong. Actu. 2, 288–294.Google Scholar
Benktander, G. (1962). Notes sur la Distribution Conditionneé du Montant d'un Sinistre par Rapport à l'Hypothèse qu'il y a eu un Sinistre dans l'Assurance Automobile, Astin Bull. 2, 24–29.CrossRefGoogle Scholar
Benktander, G. (1970). Schaden Verteilung nach Grosse in der Nicht-Leben-Versicherung, Mitt. Verein. Schweiz. Ver sich.-Mathr., 70, 268–284.Google Scholar
Buckingham, R. A. (1957), Numerical Methods, Pitman, London.Google Scholar
Cramér, H. (1926). Återförsäkring och Maximum på egen Risk, Sjunde Nord. Lifförsäk-kong., Oslo, 64–83.Google Scholar
Davis, P. J. (1964). Gamma Function and Related Functions. Ch. 6 of Handbook of Mathematical Functions, Eds. Abramowitz, M. & Stegun, I. A., N.B.S., Washington, D.C.Google Scholar
Hagstroem, K. G. (1925). La Loi de Pareto et la Réassurance,Skand. Aktuar. Tidskr., 8, 65–88.Google Scholar
Hagstroem, K. G. (1960). Remarks on Pareto Distributions, Skand. Aktuar. Tidskr., 43, 59–71.Google Scholar
Haight, F. A. (1961). Index to the Distributions of Mathematical Statistics, J. Res. Nat. Bur. Stds., 65B, 23–60.Google Scholar
Henry, M. (1937). Étude sur le Cout Moyen des Sinistres en Responsabilité Civile Automobile, Bull. Trim. Inst. Actu. Franç., 43, 113–178.Google Scholar
Jeffreys, H. (1962). Asymptotic Approximations, Oxford U.P., Oxford.Google Scholar
Johnson, N. L. and Kotz, S. (1970). Distributions in Statistics: Continuous Univariate Distributions, Houghton Mifflin, Boston.Google Scholar
Kenney, J. F. and Keeping, E. S. (1951). Mathematics of Statistics, Part Two, Van Nostrand, Princeton, New Jersey.Google Scholar
Lukacs, E. (1970). Characteristic Functions, Griffin, London.Google Scholar
Meidell, B. (1912). Zur Theorie des Maximums, Sept. Cong. Inter. Actu., 1, 85–99.Google Scholar
Meidell, B. (1938). Über eine grundlegende Frage zur Feststellung des Selbstbehalts in der Lebens- und Sachversicherung, Nordisk Forsik.-tidskr., Heft 3.Google Scholar
Oberhettinger, F. (1973). Fourier Transforms of Distributions and Their Inverses, Academic Press, New York.Google Scholar
Pagurova, V. I. (1961). Tables of the Exponential Integral, Pergamon, Oxford.Google Scholar
Patel, J. K., Kapadia, C. H. and Owen, D. B. (1976). Handbook of Statistical Distributions, Dekker, New York.Google Scholar
Pellegrin, P. (1948). Tarification de l'Assurance Automobile, Bull. Trim. Inst. Actu. Franç., 47, 19–102.Google Scholar
Seal, H. L. (1964). Actuarial Note on the Calculation of Isolated (Makeham) Joint Annuity Values, Trans. Fac. Actu., 28, 91–98.CrossRefGoogle Scholar
Seal, H. L. (1969). Stochastic Theory of a Risk Business, Wiley, New York.Google Scholar
Seal, H. L. (1978). Survival Probabilities: The Goal of Risk Theory, Wiley, Chichester.Google Scholar
Slater, L. J. (1960). Confluent Hyper geometric Functions, Cambridge U.P., Cambridge.Google Scholar
Thépaut, M. (1950). Le Traité d'Excédent du Coût Moyen Relatif (ECOMOR), Bull. Trim. Inst. Actu. Franç. 61, 273–343Google Scholar