Article contents
Some statistical aspects of catastrophic risks
Published online by Cambridge University Press: 29 August 2014
Extract
1. Risks of a catastrophic nature, such as war or earthquake, can differ, in a statistical sense, from other ordinarily insured perils only in respect of the distribution of the probability function. For example, although the probability of a loss occurring may be small, its magnitude once it occurs may be very large. One reason for the latter feature is that the sum insured may itself be heavy. But still more important is the fact that there would be strong positive correlation between similar contiguously situated risks. This is the main reason for the loss taking on a catastrophic character.
2. The fact that the probability of a loss is ordinarily small, leads to the result that the expected loss and hence the pure premium for the risk is small. Equally, and for the same reason, the “loss strain at risk” is large. If the latter could be considerably reduced—which can only be done by charging impracticably high premiums—the risk becomes more easily insurable.
3. If there are n risks of this nature, 1, 2, 3 … n and νi(x) is the conditional frequency function of the ith risk we may write
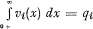
While we may imagine this as a frequency curve, the complementary probability Ϸi of a loss not occurring can be represented as a vertical line at the origin—the different methods of representation of Ϸ and q are actually convenient. With this representation, the expansion of the binomial product
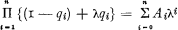
shows that the convolution of the n curves can be expressed as the sum of n + I functions
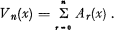
where
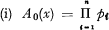
(ii) the term A1(x) comprises n separate curves of the form νi(x) each multiplied by its complementary probability, being of the form
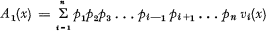
(iii) the term A2(x) comprises 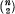 terms each consisting of the convolution of the curves taken two at a time and multiplied by the complementary probability, being of the form
terms each consisting of the convolution of the curves taken two at a time and multiplied by the complementary probability, being of the form
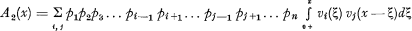
and so on.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1971
- 1
- Cited by


