When experience is insufficient to permit a direct empirical determination of the premium rates of a Stop Loss Cover, we have to fall back upon mathematical models from the theory of probability—especially the collective theory of risk—and upon such assumptions as may be considered reasonable.

The paper deals with some problems connected with such calculations of Stop Loss premiums for a portfolio consisting of non-life insurances. The portfolio was so large that the values of the premium rates and other quantities required could be approximated by their limit values, obtained according to theory when the expected number of claims tends to infinity.

The calculations were based on the following assumptions.

Let F(x, t) denote the probability that the total amount of claims paid during a given period of time is ≤ x when the expected number of claims during the same period increases from o to t. The net premium II (x, t) for a Stop Loss reinsurance covering the amount by which the total amount of claims paid during this period may exceed x, is defined by the formula

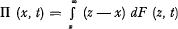
and the variance of the amount (z—x) to be paid on account of the Stop Loss Cover, by the formula

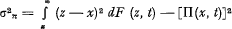
As to the distribution function F(x, t) it is assumed that

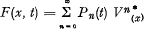
where

Pn(t) is the probability that n claims have occurred during the given period, when the expected number of claims increases from o to t,

V(x) is the distribution function of the claims, giving the conditioned probability that the amount of a claim is ≤ x when it is known that a claim has occurred, and

Vn*(x) is the nth convolution of the function V(x) with itself.

V(x) is supposed to be normalized so that the mean = I.