1. At an earlier ASTIN Colloquium participants were invited to present notes on problems which they considered as important but unsolved. There was little response to this invitation, presumably because a problem, once it is well formulated, is almost solved.

In this Note I do not present any new problems. In stead I try to outline a framework which may be useful for analysing different risk problems and seeing them in their proper perspective. In my view, a framework of this kind is urgently needed to place today's actuarial work on a sound foundation.

2. In general an insurance contract will define two stochastic processes. We lose little by assuming that the processes are discrete, and describing them in the following manner:

(i) The payment process: x0, x1 … xt …, where xt is the amount which the company pays to settle claims in period t, or at time t.

(ii) The premium process: p0, p1 … pt …, where pt is the premium which the company receives in period t, or at time t.

If the contract is concluded at time t = o, the Principle of Equivalence requires that

For the typical short-term contract with premium payable in advance (i) will reduce to

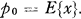
3. For a long-term insurance contract one usually requires that the inequality

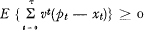
shall hold for all τ. This means that the company must never be a net creditor of its customer.