It is fantastic how the computer has changed our attitude to numerical problems. In the old days when our numerical tools were paper, pencil, desk calculator and logarithm tables we had to stay away from formulas and methods which led to too lengthy calculations. A consequence is that we have a tendency to think of numerical analysis in terms of the classical tools. If we go back to the results of earlier writers it seems, however, very likely that many results and formulas developed by them which had earlier a theoretical interest only could nowadays be applied successfully in numerical analysis.

As an example I take the ruin probability ψ(x). The Laplace transform of ψ(x) is given by the following expression

where c > 1. In fact (c — 1) is equal to the “security loading”. The function p(y) is equal to the Laplace transform of the claim distribution. We assume that the mean claim amount is equal to one, i.e. p′(0) = — 1.

In his book from 1955 [1] Cramer points out that this formula will be more easy to handle if the claim distribution is an exponential polynomial. In this case we have

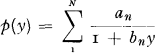
where

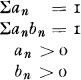
Cramér's results are given on pages 81-83 in his book. We reproduce them here with a slight change of notations only.