We will in this paper consider the risk process from the point of view of random walk in one dimension. The particle starts out at the origin. Each claim is equivalent to a step in the random walk. The length of the step is equal to the amount of the claim minus the amount of the premium which has been obtained since the preceding claim. If the difference is positive the particle advances to the right and if the difference is negative to the left. At distance U to the right from the origin there is a barrier. The problem is to find the distribution function of X, the time it takes the particle to cross the barrier for the first time.

In most practical applications of risk theory U is large in comparison to the individual steps of the particle. We will in this paper assume that U is large in comparison to the individual steps and draw certain conclusions about the risk processes from this assumption.

The individual steps of the particle have a certain distribution. The corresponding characteristic function is ϕ. For reasons which will be seen later we will consider ϕ to be a function of it = θ instead of t. This means that

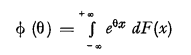
The mean value and the standard deviation of each step is equal to m and σ respectively. We now write

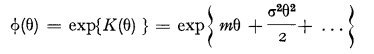
We now define two random variables X and Y.

X = time to cross the barrier for the first time

Y = X σ2/U2.