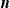1. Introduction
Reinsurance is an essential tool adopted by insurers to help mitigate risk exposure and to help stabilize business profits. It is common in the literature to design optimal reinsurance policies from the perspective of one contracting side, either insurers (i.e., reinsurance buyers) or reinsurers (i.e., reinsurance sellers); see, for example, Borch (Reference Borch1960a, Reference Borch1969) for seminal works in this area and Cai and Chi (Reference Cai and Chi2020) for a recent survey. A shortcoming of the aforementioned model is that the participation of the other side is unconditionally assumed. To address this issue, researchers adopt methods from game theory to study optimal reinsurance contracting problems, in which the interests of both contracting sides are considered. The use of game theory to model reinsurance negotiations has a long history dating back to Karl Borch. One line of research views reinsurance contracting as a cooperative game; see, Borch (Reference Borch1960b), Hürlimann (Reference Hürlimann2011), Cai et al. (Reference Cai, Fang, Li and Willmot2013, Reference Cai, Lemieux and Liu2016), and Boonen et al. (Reference Boonen, Tan and Zhuang2016), among others. Alternatively, reinsurance contracting can naturally be modeled as a non-cooperative game because insurers and reinsurers often have conflicting interests. Along this line of research, a popular formulation is a Stackelberg game (i.e., a leader–follower game), which we discuss next.
In a Stackelberg reinsurance game between an insurer and a reinsurer, the reinsurer acts as the game’s leader by offering the reinsurance premium first, the insurer acts as the game’s follower by determining the optimal indemnity in response to the given premium, and finally the reinsurer, knowing the insurer’s optimal response, chooses its optimal premium. The popularity of this model relies on the fact that the global reinsurance market is dominated by a few giant reinsurers, such as Munich Re, Swiss Re, and Hannover Re, and, thus, it is reasonable to assume that reinsurers possess more bargaining power in the contracting process and act as the leader in a Stackelberg game. The work of Chen and Shen (Reference Chen and Shen2018) is arguably the first to study such a Stackelberg reinsurance game in a continuous-time model in which both parties maximize the expected utility of their terminal surpluses. Their work is later extended in various directions, including, for instance, by Chen and Shen (Reference Chen and Shen2019) and Li and Young (Reference Li and Young2022) who consider mean-variance objectives, by Gu et al. (Reference Gu, Viens and Shen2020) and Cao et al. (Reference Cao, Li, Young and Zou2022a) who introduce model ambiguity, and by Yang et al. (Reference Yang, Zhang and Zhu2022) who incorporate information delay. The Stackelberg game model is also applied frequently in static settings, in which the reinsurance policy arising in equilibrium is called the Bowley solution; see, for example, Chan and Gerber (Reference Chan and Gerber1985) for early contributions, and Cheung et al. (Reference Cheung, Yam and Zhang2019), Li and Young (Reference Li and Young2021), Boonen et al. (Reference Boonen, Tan and Zhuang2021), Boonen and Ghossoub (Reference Boonen and Ghossoub2022), among others, for some recent developments.
All the papers mentioned in the previous paragraph consider only one reinsurer, but in practice, there usually exist multiple reinsurers in a reinsurance market, and insurers often negotiate with several reinsurers simultaneously to best suit their business objectives. There is a growing body of literature on optimal reinsurance design with multiple reinsurers in the market. See, for example, Chi and Meng (Reference Chi and Meng2014), Meng et al. (Reference Meng, Zhou and Siu2016), and (Reference Meng, Zhou and Siu2016) for studies from an insurer’s point of view, and see Asimit et al. (Reference Asimit and Boonen2018) and Boonen et al. (Reference Boonen, Tan and Zhuang2021) for papers in cooperative game settings. However, to date, the literature that applies the Stackelberg framework to model reinsurance contracting with multiple reinsurers is scarce, including, to the best of our knowledge, only Lin et al. (Reference Lin, Liu, Liu and Yu2022) and Cao et al. (Reference Cao, Li, Young and Zou2023a), despite the naturalness in formulating the problem this way. Although differing in several major aspects (see Cao et al., Reference Cao, Li, Young and Zou2023a for a summary of the differences), both papers (i.e., Lin et al., Reference Lin, Liu, Liu and Yu2022 and Cao et al., Reference Cao, Li, Young and Zou2023a) investigate reinsurance contracting between one insurer and two reinsurers, assuming the reinsurers compete for the reinsurance business, and they find that the insurer benefits from the competition. This work raises two further questions: Will the insurer, in general, benefit when the number of competing reinsurers increases? If the answer is yes, what are the fundamental reasons behind it? To address these questions, it is necessary to consider a reinsurance market consisting of n reinsurers, with
$n \ge 2$
being an arbitrary integer.
While the above questions may be answered from various perspectives, we focus on the effect of ambiguity in this paper. Ambiguity is a concept that is at least as important as risk in making reinsurance decisions. Regarding risk, finance literature supports the assumption that insurers and reinsurers are risk neutral (see, e.g., Rothschild and Stiglitz, 1986); however, they are to some extent uncertain about the underlying risk exposure due to reasons such as imperfect information and insufficient data; thus, they are ambiguity averse (see Hansen and Sargent, Reference Hansen and Sargent2001). To account for ambiguity, robust optimal reinsurance problems are studied in, for instance, Li et al. (Reference Li, Zeng and Yang2018) and Hu et al. (Reference Hu, Chen and Wang2018a,Reference Hu, Chen and Wangb). We follow the ambiguity model in Cao et al. (Reference Cao, Li, Young and Zou2023a) to study robust reinsurance contracting and competition in a reinsurance market with one primary insurer and multiple (i.e., possibly more than 2) reinsurers in a continuous-time model. The insurer negotiates reinsurance policies with all reinsurers simultaneously, leading to a tree structure, and the reinsurers compete with each other. All companies are ambiguous about the insurance risk assumed by the insurer, aiming to maximize their expected terminal surplus over a random time horizon, plus a squared-error penalty term reflecting ambiguity.
Similar to Cao et al. (Reference Cao, Li, Young and Zou2023a), and Lin et al. (Reference Lin, Liu, Liu and Yu2022), we model the reinsurance contracting problems between the insurer and reinsurers by Stackelberg differential games and the competition among reinsurers by a non-cooperative Nash game. Unlike these two papers, in which the two reinsurers are mainly distinguished by their premium principles, here we assume the reinsurers all apply the variance premium principle and are distinguished only by their ambiguity aversion parameters. There are several advantages for such a modeling choice. First, this allows us to consider the general case of n reinsurers, with an arbitrary n, and further study how the market size n affects the insurer and reinsurers’ equilibrium decisions. However, neither of these is possible, if we were to follow Cao et al. (Reference Cao, Li, Young and Zou2023a) and Lin et al. (Reference Lin, Liu, Liu and Yu2022) to differentiate reinsurers by premium principles, because only a limited number of such principles are available and the effect of adding one reinsurer on the existing players’ decisions is hard, if not impossible, to analyze. Second, we are able to isolate the impact of ambiguity on equilibrium in the setup in this paper. Note that such a task is challenging in Cao et al. (Reference Cao, Li, Young and Zou2023a) because the choice of premium principles (expected-value vs. variance) also affects the equilibrium controls.
We next discuss the main contributions of the paper. First, to the best of our knowledge, this is the first paper to study reinsurance contracting and competition in a continuous-time model with an arbitrary number of reinsurers. We obtain equilibrium strategies for all players in semi-closed form and find that the insurer buys a positive amount of proportional reinsurance from each reinsurer (see Theorem 3.3).
Second, we examine the effect of increasing the market size n and show that the premiums offered by reinsurers decrease when n increases, that is, competition drives down the reinsurance premium. Moreover, as n increases, the insurer buys more reinsurance in total. In other words, the insurer benefits from a larger reinsurance market with more intense competition and lower prices and, therefore, cedes a larger portion of risk in aggregate to the reinsurers.
Third, this paper and our previous work Cao et al. (Reference Cao, Li, Young and Zou2023a) are the only ones, to our awareness, that investigate the optimality of reinsurance structures. Here, a structure refers to the way a reinsurance market of one insurer and n reinsurers is formed; recall that the first part of our analysis assumes a priori that the reinsurance market forms a tree structure, with the insurer buying reinsurance from n reinsurers simultaneously. In the second part, we also consider an alternative structure, namely, a chain structure,Footnote 1 in which the risk of the primary insurer is shared sequentially among all n reinsurers, and we compare the tree and chain structures from the insurer’s perspective. A structure is preferred if it leads to a higher equilibrium value function for the insurer. Comparing the tree and chain structures is interesting because they represent two extreme cases, that is, the one with full competition (the tree) and the one with no competition (the chain). We first solve the n Stackelberg reinsurance games under the chain structure and obtain all equilibrium controls explicitly; see Theorem 4.1. Next, we show in Theorem 4.2 that, among all
$n!$
possible chains, the optimal chain is the one in which the reinsurers are arranged according to their ambiguity parameters in an increasing order.Footnote 2 Last, we prove that the insurer always prefers the tree structure to the chain structure, by showing the equilibrium value function under the tree structure is greater than that under the optimal chain structure; see Theorem 4.3. Note that such a definite preference result is not available in Cao et al. (Reference Cao, Li, Young and Zou2023a), in which there exist certain scenarios for which the chain structure is preferable to the tree structure.
The remainder of the paper is organized as follows. In Section 2, we formulate the robust reinsurance contracting and competition problems. In Section 3, we derive the equilibrium under the tree structure in semi-closed form and conduct a comparative statics analysis with respect to the ambiguity aversion parameters. In Section 4, we derive the equilibrium under the chain structure and subsequently show that the primary insurer prefers the tree over the chain. Section 5, then, concludes the paper. Proofs for Sections 3 and 4 are placed in Appendices A and B, respectively.
2. Reinsurance tree: model
2.1. Reinsurance market
We consider a reinsurance market consisting of
$n+1$
players, labeled by
$i =0, 1, \dots, n$
; player 0 is the primary insurer and the remaining n players are reinsurers. Throughout this paper, we assume that n is at least 2. The insurer negotiates reinsurance policies with all n reinsurers simultaneously, forming a reinsurance tree. On a fixed probability space
$\big(\Omega, \mathcal{F}, \mathbb{F} = \{\mathcal{F}(t) \}_{t \ge 0}, \mathbb{P} \big)$
, we model the insurer’s uncontrolled surplus by:
\begin{equation} \mathrm{d} U(t) = c \, \mathrm{d} t - \int_0^\infty z N(\mathrm{d} z, \mathrm{d} t),\end{equation}
in which
$c>0$
is the income rate and
$N(\cdot, \cdot)$
is a Poisson random measure whose associated Lévy measure
$\nu$
satisfies
\begin{align*} \int_0^\infty (z \vee z^2) \nu(\mathrm{d} z) < \infty.\end{align*}
Without loss of generality, assume
$\nu$
does not place all its mass at
$z = 0$
.
The primary insurer transfers part of its risk to the n reinsurers via per-claim reinsurance. For
$i = 1, 2, \dots, n$
, let
$I_i$
represent the indemnity that the insurer purchases from reinsurer i, and we assume
$I_i = I_i(z)$
is a deterministic function of the claim size z and is time-independent.Footnote 3 The insurer’s admissible indemnities are defined as follows.
Definition 2.1 (Admissible indemnities). An n-tuple of indemnities
$I\,:\!=\, (I_1, I_2, \dots, I_n)$
is admissible if (i)
$I_i$
, for
$i = 1, 2, \dots, n$
, is a nonnegative, Borel-measurable function of
$z \in \mathbb{R}_+$
, and (ii)
$\sum_{i=1}^n I_i(z) \le z$
for all
$z \in \mathbb{R}_+$
. Let
$\mathcal{I}$
denote the set of admissible I.
We assume all n reinsurers apply the variance premium principle in pricing their policies, with possibly different loadings. Specifically, reinsurer i charges premiums at a continuous rate given by:
\begin{equation*} \pi_i(I_i) = \int_0^\infty \left\{ I_i(z) + \dfrac{\eta_i}{2} \, I_i^2(z) \right\} \nu(\mathrm{d} z),\end{equation*}
in which
$\eta_i$
denotes the reinsurer i’s premium loading and is assumed to be a nonnegative constant. If
$\eta_i$
were allowed to be a deterministic function of the claim size z, then the optimal
$\eta_i$
would be a constant; see Theorem 3.2 in Cao et al. (Reference Cao, Li, Young and Zou2023a). Therefore, to simplify notation, we assume
$\eta_i$
is a constant from the outset, for all
$i = 1, 2, \dots, n$
. We also assume that each reinsurer knows the other’s premium rule, although they do not cooperate in choosing their premium loadings. Indeed, we assume the reinsurers compete with each other in choosing their premium loadings.
In the following, we write
$\vec{\eta} = (\eta_1, \eta_2, \dots, \eta_n)$
to denote the n-tuple of premium loadings for all reinsurers, and we write
$\vec{\eta}_{(i)}$
to denote the
$(n-1)$
-tuple of premium loadings that excludes
$\eta_i$
, for
$i = 1, 2, \dots, n$
.
Remark 2.1. Reinsurers can be distinguished by premium rules; see, for example, Meng et al. (Reference Meng, Siu and Yang2016) and Lin et al. (Reference Lin, Liu, Liu and Yu2022). Especially, Cao et al. (Reference Cao, Li, Young and Zou2023a) consider a reinsurance tree structure with two reinsurers, in which one reinsurer adopts the expected-value premium principle and the other adopts the variance premium principle. In certain cases, distinguishing reinsurers by premium rules is necessary to guarantee the existence of equilibrium. For example, if all reinsurers apply the expected-value premium principle, then no equilibrium exists. In that case, one can show that the Nash equilibrium dictates that all the premium loadings
$\theta$
s are equal, but that means the insurer buys
$(z - \theta/\varepsilon_0)_+$
in total, and the reinsurers are not able to find their optimal value of
$\theta$
because any allocation of
$(z - \theta/\varepsilon_0)_+$
among the reinsurers is possible.Footnote 4 However, if all the reinsurers apply the variance premium principle, an equilibrium does exist. We will see later that, in equilibrium, the insurer purchases a positive amount from each reinsurer, even though each reinsurer uses the same type of premium rule.
We further incorporate model uncertainty into the reinsurance market by assuming that all
$n+1$
players are ambiguous about the Poisson random measure N, which captures the insurer’s original risk, as given in (2.1). To that end, we introduce a probability distortion
$\phi = \phi(z)$
, and define a new probability measure
$\mathbb{Q}^\phi$
by
$\frac{\mathrm{d} \mathbb{Q}^\phi}{\mathrm{d} \mathbb{P}} \big|_{\mathcal{F}(t)} \,=\!:\, \Lambda^\phi(t)$
,Footnote 5 in which
\begin{align*} \ln \Lambda^\phi(t) &= \int_0^t \int_0^\infty \ln(1 + \phi(z)) \widetilde N^\phi(\mathrm{d} z, \mathrm{d} s) + t \int_0^\infty \big( (1 + \phi(z)) \ln(1 + \phi(z)) - \phi(z) \big) \nu(\mathrm{d} z).\end{align*}
In the above,
$\widetilde N^\phi$
is a
$\mathbb{Q}^\phi$
-compensated random measure with compensator
$(1 + \phi(z))\nu(\mathrm{d} z) \mathrm{d} t$
under
$\mathbb{Q}^\phi$
and is defined by:
\begin{equation} \widetilde N^\phi(\mathrm{d} z, \mathrm{d} t) \,:\!=\, N(\mathrm{d} z, \mathrm{d} t) - \big(1 + \phi(z) \big) \nu(\mathrm{d} z) \mathrm{d} t.\end{equation}
Definition 2.2 (Admissible probability distortions). A probability distortion
$\phi$
is admissible if (i)
$\phi$
is a nonnegative, Borel-measurable function of
$z \in \mathbb{R}_+$
and (ii)
$\phi$
satisfies the conditions:
\begin{align*}\int_0^\infty \big( (1 + \phi(z)) \ln(1 + \phi(z)) - \phi(z) \big) \nu(\mathrm{d} z) < \infty,\end{align*}
and
\begin{equation*}\int_0^\infty z \big(1 + \phi(z) \big) \nu(\mathrm{d} z) < \infty.\end{equation*}
Let
$\Phi$
denote the set of admissible probability distortions
$\phi$
.
Let
$\phi_i$
and
$X_i = \{X_{i}(t)\}_{t \ge 0}$
denote the probability distortion and the surplus process of player i, respectively, for
$i = 0, 1, 2, \dots, n$
. The dynamics of the primary insurer’s surplus
$X_0 =\{X_0(t)\}_{t \ge 0}$
under
$\mathbb{Q}^{\phi_0}$
is given by:
\begin{align} \mathrm{d} X_0(t) &= c \, \mathrm{d} t - \int_0^\infty \left\{z - \sum_{i=1}^n I_i(z) \right\} \widetilde N^{\phi_0}(\mathrm{d} z, \mathrm{d} t) - \int_0^\infty \left\{ z - \sum_{i=1}^n I_i(z) \right\} \big( 1 + \phi_0(z) \big) \, \nu(\mathrm{d} z) \mathrm{d} t \notag \\[5pt] &\quad - \int_0^\infty \left\{ \sum_{i=1}^n \left( I_i(z) + \dfrac{\eta_i}{2} \, I_i^2(z) \right) \right\} \nu(\mathrm{d} z) \mathrm{d} t.\end{align}
Next, the surplus process of reinsurer i,
$X_i = \{X_i(t)\}_{t \ge 0}$
, follows the
$\mathbb{Q}^{\phi_i}$
-dynamics:
\begin{align} \mathrm{d} X_i(t) &= - \int_0^\infty I_{i}(z) \widetilde N^{\phi_i}(\mathrm{d} z, \mathrm{d} t) + \int_0^\infty \left\{\dfrac{\eta_i}{2} \, I_i^2(z) - \phi_i(z) I_{i}(z) \right\} \nu(\mathrm{d} z) \mathrm{d} t,\end{align}
for
$i = 1, 2, \dots, n$
. In both (2.3) and (2.4),
$\widetilde N^{\phi_i}$
is defined by (2.2) under the corresponding
$\phi_i$
.
2.2. Problem formulation
Because all players are for-profit (re)insurance companies, we assume each is risk-neutral under its respective distorted probability measure, that is, player i aims to maximize its expected surplus under
$\mathbb{Q}^{\phi_i}$
, for all
$i=0,1,\dots,n$
(see Remark 2.2 in Cao et al., Reference Cao, Li, Young and Zou2023b for justifications of this objective). To account for model ambiguity, a penalty term is added to each player’s objective; here, we follow Cao et al. (Reference Cao, Li, Young and Zou2022a,Reference Cao, Li, Young and Zoub, Reference Cao, Li, Young and Zou2023a) and use squared-error divergence to measure the deviation from the reference model
$\mathbb{P}$
due to its interpretability and tractability (see Remark 2.3 in Cao et al., Reference Cao, Li, Young and Zou2022a for a detailed discussion). We formulate all reinsurance games under the same random horizon
$\tau$
, which, for instance, can be interpreted as the insurer’s next regulatory assessment time. We assume
$\tau$
is an
$\mathcal{F}$
-measurable random variable, independent of the Poisson random measure N, and has a deterministic hazard rate
$\rho(t) > 0$
, with
\begin{equation}\mathbb{P}(\tau > t) = \mathbb{Q}^{\phi}(\tau > t) = \mathrm{e}^{-\int_0^t \rho(s) \mathrm{d} s},\end{equation}
for
$t \ge 0$
and
$\phi \in \Phi$
, in which the first equality is due to the independence assumption. Finally, we assume
$\mathbb{E}^\mathbb{P}(\tau) < \infty$
.
We are now ready to present the primary insurer’s robust reinsurance problem. Given an n-tuple of premium loadings
$\vec{\eta}$
from the n reinsurers, the insurer seeks optimal indemnities
$I^*(\cdot;\, \vec{\eta})$
and optimal distortion
$\phi_0^*(\cdot;\, \vec{\eta})$
by solving
\begin{equation} \mathcal{V}_0(x_0, t;\, \vec{\eta}) = \sup \limits_{I \in \mathcal{I}} \,\inf \limits_{\phi_0 \in \Phi} \; \mathbb{E}^{\phi_0}_{x_0,t} \bigg( X_0(\tau) + \dfrac{\tau - t}{2\varepsilon_0} \int_0^\infty \phi_0^2(z) \, \nu(\mathrm{d} z) \, \bigg| \, \tau > t \bigg),\end{equation}
in which
$\mathbb{E}^{\phi_0}_{x_0, t}$
denotes conditional expectation under
$\mathbb{Q}^{\phi_0}$
given
$X_0(t^-)=x_0$
,Footnote 6
$\varepsilon_0 >0$
is the insurer’s coefficient of ambiguity aversion, and the surplus process
$X_0$
is defined by (2.3).
We next formulate the reinsurers’ robust reinsurance problems. Upon knowing the other reinsurers’ premium loadings
$\vec{\eta}_{(i)}$
, reinsurer i (for
$i = 1, 2, \dots, n$
) obtains its optimal premium loading
$\bar{\eta}_i(\vec{\eta}_{(i)})$
and optimal probability distortion
$\bar{\phi}_i(\vec{\eta}_{(i)})$
by solving
\begin{equation} \mathcal{V}_i(x_i, t;\, \vec{\eta}_{(i)}) = \sup \limits_{\eta_i \ge 0} \, \inf \limits_{\phi_i \in \Phi} \; \mathbb{E}^{\phi_i}_{x_i, t} \bigg(X_i(\tau) + \dfrac{\tau - t}{2\varepsilon_i}\ \int_0^\infty \phi_i^2(z) \, \nu(\mathrm{d} z) \, \bigg| \, \tau > t \bigg),\end{equation}
in which
$\mathbb{E}^{\phi_i}_{x_i, t}$
denotes conditional expectation under
$\mathbb{Q}^{\phi_i}$
given
$X_i(t^-)=x_i$
,
$\varepsilon_i > 0$
is the coefficient of ambiguity aversion of reinsurer i, and
$X_i$
follows the process in (2.4) with
$I_i$
replaced by the optimal indemnity
$I^*_i(\cdot;\, \vec{\eta})$
from (2.6).
We model the reinsurance contracting problem between the primary insurer and reinsurer i by a Stackelberg differential game, in which the reinsurer is the leader and the insurer is the follower. Due to this setup, the insurer’s optimal strategies from solving (2.6) are known to all reinsurers, justifying the replacement of
$I_i$
by
$I^*_i(\cdot;\, \vec{\eta})$
in (2.7). The n reinsurers compete for business from the insurer, and this competition is reflected in two places. First, the insurer’s optimal indemnity with reinsurer i,
$I^*_i(\cdot;\, \vec{\eta})$
, depends not only on the reinsurer i’s loading
$\eta_i$
but also on other reinsurers’ loadings
$\vec{\eta}_{(i)}$
; second, reinsurer i solves (2.7) to find its optimal strategies based on other reinsurers’ premium loadings
$\vec{\eta}_{(i)}$
. We formally model the reinsurance competition problem among n reinsurers by a non-cooperative Nash game. In consequence, a Nash equilibrium is achieved if
$\vec{\eta}$
is a fixed point of the mapping
$\vec{\eta} \mapsto \big( \bar{\eta}_1(\vec{\eta}_{(1)}), \bar{\eta}_2(\vec{\eta}_{(2)}), \dots, \bar{\eta}_n(\vec{\eta}_{(n)}) \big)$
, in which
$\bar{\eta}_i(\vec{\eta}_{(i)})$
is the optimizer of (2.7) for
$i=1,2,\dots,n$
. To summarize, we apply a two-layer game framework to study the reinsurance contracting and competition in a tree structure: the n parallel reinsurance contracting problems between the insurer and n reinsurers are modeled by n Stackelberg differential games, and the reinsurance competition among n reinsurers is settled by a non-cooperative Nash game. Please refer to Cao et al. (Reference Cao, Li, Young and Zou2023a) for a more detailed description of a similar game framework.
Definition 2.3 (Equilibrium). The equilibrium of the reinsurance contracting and competition games is the following collection of controls: the Nash equilibrium of premium loadings
$\vec{\eta}^*=(\eta^*_1, \eta^*_2, \dots, \eta^*_n)$
is given by
$\eta^*_i = \bar\eta_i(\vec{\eta}^{*}_{(i)}) \ge 0$
for
$i =1, 2, \dots, n$
, in which
$\bar\eta_i(\cdot)$
is obtained from solving (2.7);
$\phi^*_i = \phi^*_i(\cdot \, ;\, \vec{\eta}^{*}) \in \Phi$
for
$i = 1, 2, \dots, n$
, which achieves the infimum in (2.7);
$I^* = \big(I^*_1(\cdot \, ;\, \vec{\eta}^{*}), I^*_2(\cdot \, ;\, \vec{\eta}^{*}), \dots, I^*_n(\cdot\,;\, \vec{\eta}^{*}) \big) \in \mathcal{I}$
, which achieves the supremum in (2.6); and,
$\phi^*_0 = \phi^*_0(\cdot \, ;\, I^*, \vec{\eta}^{*}) \in \Phi$
, which achieves the infimum in (2.6). We also define the insurer’s equilibrium value function by
$V_0(x_0, t) \,:\!=\, \mathcal{V}(x_0, t;\, \vec{\eta}^*)$
and reinsurer i’s equilibrium value function by
$V_i(x_i, t) = \mathcal{V}_i(x_i, t;\, \vec{\eta}^{*}_{(i)})$
for
$i = 1, 2, \dots, n$
.
3. Reinsurance tree: equilibrium
In this section, we obtain the equilibrium controls for all the players (one insurer and n reinsurers) semi-explicitly. To improve readability, we place all the proofs of this section in Appendix A.
First, we solve the insurer’s problem in (2.6) and obtain its optimal strategies given
$\vec{\eta}$
, as summarized in the following theorem.
Theorem 3.1.
Given an n-tuple of positive premium loadings
$\vec{\eta} = (\eta_1, \eta_2, \dots, \eta_n)$
, the insurer’s optimal probability distortion equals
\begin{equation}\phi_0^*(z;\, I, \vec{\eta}) = \varepsilon_0 \left(z - \sum_{i=1}^n I_i(z;\, \vec{\eta}) \right).\end{equation}
The optimal collection of indemnities equals
$I^*(z;\,\vec{\eta}) = \big(I^*_1(z;\,\vec{\eta}), I^*_2(z;\,\vec{\eta}), \dots, I^*_n(z;\, \vec{\eta})\big)$
, in which
\begin{equation}I^*_i(z;\, \vec{\eta}) = \dfrac{\frac{\varepsilon_0}{\eta_i}}{1 + \sum_{j=1}^n \frac{\varepsilon_0}{\eta_j}} \, z.\end{equation}
Theorem 3.1 presents the solution of the insurer’s problem in (2.6) when all premium loadings are positive (that is,
$\eta_i > 0$
for all
$i=1,2,\dots,n)$
and omits the cases for which
$\eta_i = 0$
for some
$i=1,2,\dots,n$
. Note that the optimal indemnities
$I^*_i(z;\, \vec{\eta})$
in (3.2) are only well defined when all loadings are positive. If some loadings equal 0, a more involved analysis is required to derive
$I^*_i(z;\, \vec{\eta})$
, which we show in Appendix A.1. However, if
$\eta_i = 0$
were allowed, then we would find, from solving the reinsurers’ problem in (2.7), that it is never optimal for a reinsurer to offer reinsurance with a zero loading (see Proposition A.1). The optimal indemnities
$I^*_i(z;\, \vec{\eta})$
in (3.2) are of proportional type for all i and are consistent with the findings in Cao et al. (Reference Cao, Li, Young and Zou2023a), in which the insurer buys proportional reinsurance from the reinsurer who adopts a variance premium principle.
Next, we study reinsurer i’s problem (2.7) and present its solution in the following theorem.
Theorem 3.2.
Given an n-tuple of positive premium loadings
$\vec{\eta} = (\eta_1, \eta_2, \dots, \eta_n)$
, the optimal probability distortion of reinsurer i, for
$i = 1, 2, \dots, n$
, equals
\begin{equation} \phi^*_i(z;\, \vec{\eta}) = \varepsilon_i I^*_i(z;\,\vec{\eta}), \end{equation}
in which
$I^*_i(z;\, \vec{\eta})$
is given by (3.2). Moreover, given an
$(n-1)$
-tuple of positive premium loadings
$\vec{\eta}_{(i)} = (\eta_1, \dots, \eta_{i-1}, \eta_{i+1}, \dots, \eta_n)$
, the optimal premium loading
$\bar{\eta}_i (\vec{\eta}_{(i)})$
of reinsurer i, for
$i=1,2,\dots,n$
, equals
\begin{align} \bar{\eta}_i (\vec{\eta}_{(i)}) = \frac{\varepsilon_0 + 2 \varepsilon_i}{1 + \sum_{j \neq i} \frac{\varepsilon_0}{\eta_j}} . \end{align}
The reinsurance market in consideration is perfect, in the sense that reinsurer i observes other reinsurers’ loadings
$\vec{\eta}_{(i)}$
and chooses its optimal loading
$\bar{\eta}_i (\vec{\eta}_{(i)})$
by (3.4). In our formulation, the reinsurance competition among the n reinsurers is modeled by a non-cooperative Nash game, and its equilibrium
$\vec{\eta}^*$
is a fixed point of
$\eta^*_i = \bar{\eta}_i (\vec{\eta}_{(i)}^*)$
for all
$i=1,2,\dots, n$
, as stated in Definition 2.3. The next theorem finds such an equilibrium of premium loadings
$\vec{\eta}^*$
; other equilibrium controls, such as
$I_i^*$
, can be easily obtained by replacing
$\vec{\eta}$
with
$\vec{\eta}^*$
and, thus, are not stated. See Appendix A.3 for the theorem’s proof.
Theorem 3.3.
The equilibrium premium loading of reinsurer i, for
$i=1,2,\dots,n$
, equals
\begin{equation} \eta_i^* = \frac{2 \varepsilon_0 \varepsilon_i}{\varepsilon_0 + \varepsilon_i (1 + \varepsilon_0 \alpha^*) - \sqrt{ \varepsilon_0^2 + \varepsilon_i^2 (1 + \varepsilon_0 \alpha^*)^2 }}, \end{equation}
in which
$\alpha^* = \sum_{i=1}^n \, \frac{1}{\eta_i^*}$
is the unique positive zero of the function
$\mathfrak{h}$
defined by:
\begin{equation} \mathfrak{h}(\alpha) = \frac{n}{2 \varepsilon_0} + \dfrac{n-2}{2} \, \alpha + \frac{1}{2} \sum_{i=1}^n \, \left(\frac{1}{\varepsilon_i} - \sqrt{\frac{1}{\varepsilon_i^2} + \left(\frac{1}{\varepsilon_0} + \alpha \right)^2 }\right). \end{equation}
Then, the equilibrium value function of reinsurer i, for
$i = 1, 2, \dots, n$
, equals
\begin{equation*} V_i(x_i,t) = x_i + v_i(t),\end{equation*}
in which
\begin{equation*} v_i(t) = \dfrac{\eta^*_i-\varepsilon_i}{2} \left(\dfrac{\frac{\varepsilon_0}{\eta^*_i}}{1 + \sum_{j=1}^n \frac{\varepsilon_0}{\eta^*_j}}\right)^2\int_0^\infty z^2 \nu(\mathrm{d} z) \cdot \mathbb{E}( \tau - t | \tau > t ).\end{equation*}
The sum of the insurer’s equilibrium indemnities equals
\begin{align} \mathbb{I}^*(z) \,:\!=\, \sum_{i=1}^n \, I_i^*(z) = \frac{\varepsilon_0 \alpha^*}{1 + \varepsilon_0 \alpha^*} \, z.\end{align}
Moreover, the insurer’s equilibrium value function equals
\begin{align} V_0(x_0, t) = x_0 + v_0(t),\end{align}
in which
\begin{align} v_0(t) = \int_0^\infty \Big( c - z - \dfrac{\varepsilon_0}{2(1+\varepsilon_0 \alpha^*)} \,z^2\Big) \nu(\mathrm{d} z) \cdot \mathbb{E}(\tau - t| \tau >t).\end{align}
We end this section with several remarks about the equilibrium found in Theorem 3.3.
If
$\varepsilon_i = \varepsilon > 0$
for all
$i=0,1,\dots,n$
, then all reinsurers will adopt the same equilibrium loading
$\eta^*$
, which is given by: We easily see that, as the ambiguity aversion
\begin{align*} \eta^* = \frac{4 \varepsilon (n - 1)}{n - 4 + \sqrt{n^2 + 8}}. \end{align*}
$\varepsilon$
increases, the equilibrium loading
$\eta^*$
increases. If we further treat n, the number of competing reinsurers, as a variable, we find that
$\eta^*$
is a decreasing function of n. As a result, when reinsurance competition intensifies, reinsurers lower their premium loadings. From (3.7) and (3.9), we see that, when n increases, both
$\mathbb{I}^*(z)$
and
$V_0$
increase, implying that the insurer benefits from the reinsurance competition and prefers a larger reinsurance market. In the limit case, suggesting that the insurer will cede all of its risk to reinsurers.
\begin{align*} \lim_{ n \to \infty} \, \eta^* = \varepsilon \quad \text{ and } \quad \lim_{ n \to \infty} \, \mathbb{I}^*(z) = z,\end{align*}
Next, continue to assume
$\varepsilon_i = \varepsilon$
for all
$i=1,2,\dots,n$
, but allow
$\varepsilon_0$
to differ. In other words, all reinsurers have the same ambiguity aversion, but the insurer might have a different ambiguity aversion. Again, by (3.4), we conclude that all n reinsurers will have the same equilibrium loading
$\eta_i = \eta^*$
, which is the positive solution of
$\eta^2 - \big( (n-2) \varepsilon_0 - 2 \varepsilon \big) \eta - 2(n-1) \varepsilon_0 \varepsilon = 0$
and can be obtained explicitly. Given
$\varepsilon = 0.1$
, we plot in Figure 1 the graphs of the equilibrium loading
$\eta^*$
as
$\varepsilon_0$
varies over
$(0, 0.5)$
, for different values of n (here we consider
$n=3, 5, 10$
). By comparing the three curves, we see that
$\eta^*$
decreases as n increases; in consequence, the economic explanations about n that we made above apply here as well. Next, for a fixed value of n, one can show that
$\eta^*$
increases as
$\varepsilon_0$
increases. Thus, when the insurer is more ambiguity averse about the risk, all reinsurers will increase their premium loadings, and the magnitude of adjustment is more significant when n is small.Figure 1. Equilibrium loading
$\eta^*$
when
$\varepsilon_i = 0.1$
for
$i=1,2,\dots,n$
.We continue our study by assuming
$\varepsilon_i = \varepsilon$
for
$i=1,2,\dots, n - 1$
and by allowing both
$\varepsilon_n$
and
$\varepsilon_0$
to differ from
$\varepsilon$
. To understand this case, consider a reinsurance market with
$n-1$
homogeneous reinsurers, all with the same ambiguity aversion
$\varepsilon$
; then, a new reinsurer with ambiguity aversion
$\varepsilon_n$
, referred to as reinsurer n, joins the reinsurance market. In this case, the equilibrium loadings of reinsurers 1 to
$n-1$
equal, denoted by
$\eta^*$
(or
$\eta^* |_{n}$
to emphasize the market size), but reinsurer n’s equilibrium loading
$\eta^*_n$
is possibly different from
$\eta^*$
. To see how
$\varepsilon_n$
impacts the equilibrium loadings, we fix
$\varepsilon_i = 0.1$
for
$i=0,1,\dots,n-1$
with
$n = 5$
. In Figure 2, we plot the equilibrium loadings as
$\varepsilon_n$
varies over
$(0, 0.2)$
. We first consider the “original” market with
$n-1$
homogeneous reinsurers and calculate the equilibrium loading
$\eta^* |_{n=4} = 0.2449$
, which corresponds to the horizontal line in dotted black in Figure 2. Next, we consider the “new” market with reinsurer n, whose ambiguity aversion
$\varepsilon_n$
might be different from the existing reinsurers’
$\varepsilon$
. In this new market, we plot
$\eta^*_n |_{n=5}$
in blue and
$\eta_i^*|_{n=5}$
in red, for
$i = 1, 2, 3, 4$
. The most important finding is that the
$(n-1)$
existing reinsurers will always lower their equilibrium loading, regardless of the new reinsurer’s ambiguity aversion
$\varepsilon_n$
, which is a direct consequence of competition. Therefore, our earlier conclusion still holds, that is, the insurer prefers a larger reinsurance market. We also notice the intersection point at
$\varepsilon_n=0.1$
, meaning if reinsurer n shares the same ambiguity aversion as the rest
$n-1$
reinsurers, their equilibrium loadings will be the same as well. Figure 2 also shows that, when
$\varepsilon_n$
increases, both
$\eta^*_n$
and
$\eta^*$
increase, although they react at dramatically different scales.Figure 2. Equilibrium loadings
$\eta^*_n$
of reinsurer n and
$\eta_i^*$
of reinsurer i.
4. Reinsurance chain
In this section, we study the chain structure for these
$n+1$
players. The primary insurer (player 0) purchases a reinsurance policy from reinsurer 1; reinsurer 1 then acts as the ceding company and purchases a reinsurance policy from reinsurer 2; this reinsurance chain continues until the last reinsurance contract between reinsurer
$n-1$
and reinsurer n. The surplus dynamics of the primary insurer and the n reinsurers under the chain structure differs from (2.3) and (2.4) under the tree structure. For this reason, we add an overhead hat to notation under the chain structure; for example,
$\hat X_i$
denotes the surplus process of player i under the chain structure. The surplus process of the insurer
$\hat X_0 = \{X_0(t)\}_{t \ge 0}$
follows the
$\mathbb{Q}^{\phi_0}$
-dynamics:
\begin{align*} \mathrm{d} \hat X_0(t) &= c \, \mathrm{d} t - \int_0^\infty \big(z - I_1(z) \big) \widetilde N^{\phi_0}(\mathrm{d} z, \mathrm{d} t) - \int_0^\infty \big( z - I_1(z) \big) \big( 1 + \phi_0(z) \big) \, \nu(\mathrm{d} z) \mathrm{d} t \notag \\ &\quad - \int_0^\infty \left\{ I_1(z) + \dfrac{\eta_1(z)}{2} \, I_1^2(z) \right\} \nu(\mathrm{d} z) \mathrm{d} t,\end{align*}
in which
$I_1$
is the indemnity function of the first game, between the primary insurer and reinsurer 1. The surplus process of intermediate reinsurer i,
$X_i = \{X_i(t)\}_{t \ge 0}$
, for
$i = 1, 2, \dots, n-1$
, follows the
$\mathbb{Q}^{\phi_i}$
-dynamics:
\begin{align} \mathrm{d} \hat X_i(t) &= - \int_0^\infty \big(I_i(z) - I_{i+1}(z)\Big) \widetilde N^{\phi_i}(\mathrm{d} z, \mathrm{d} t) + \int_0^\infty \left\{ \dfrac{\eta_i(z)}{2} \, I_{i}^2(z) - \phi_i(z) I_{i}(z) \right\} \nu(\mathrm{d} z) \mathrm{d} t \notag\\ &\quad - \int_0^\infty \left\{ \dfrac{\eta_{i+1}(z)}{2} \, I_{i+1}^2(z) - \phi_i(z) I_{i+1}(z) \right\} \nu(\mathrm{d} z) \mathrm{d} t,\end{align}
In (4.1), reinsurer i sells indemnity
$I_i$
to (re)insurer
$i-1$
and purchases indemnity
$I_{i+1}$
from reinsurer
$i+1$
. Finally, the terminal reinsurer’s surplus process
$X_n=\{X_n(t)\}_{t\geq0}$
follows the
$\mathbb{Q}^{\phi_n}$
-dynamics:
\begin{align*} \mathrm{d} \hat X_n(t) &= - \int_0^\infty I_{n}(z) \widetilde N^{\phi_n}(\mathrm{d} z, \mathrm{d} t) + \int_0^\infty \left\{ \dfrac{\eta_n(z)}{2} \, I_n^2(z) - \phi_n(z) I_n(z) \right\} \nu(\mathrm{d} z) \mathrm{d} t. \hspace{4ex}\end{align*}
Instead of requiring
$\sum_{i=1}^n I_i(z) \le z$
for all
$z \ge 0$
as in Definition 2.1, we require that admissible indemnities in this setting satisfy
$0 \le I_n(z) \le I_{n-1}(z) \cdots \le I_2(z) \le I_1(z) \le z$
for all
$z \ge 0$
. These inequalities arise as the “intersection” of the standard indemnity conditions for n sequential reinsurance problems. Label the admissible indemnities by
$\hat {\mathcal{I}}$
.
The primary insurer’s robust optimal reinsurance problem is
\begin{equation}\hat{\mathcal{V}}_0(x_0, t;\, \eta_1) = \sup \limits_{I_1 \in \hat{\mathcal{I}}} \, \inf \limits_{\phi_0 \in \Phi} \; \mathbb{E}^{\phi_0}_{x_0,t} \bigg( \hat X_0(\tau) + \dfrac{\tau - t}{2\varepsilon_0} \int_0^\infty \phi_0^2(z) \, \nu(\mathrm{d} z) \, \bigg| \, \tau > t \bigg).\end{equation}
For
$i = 1, 2, \dots, n-1$
, intermediate reinsurer i’s robust optimal reinsurance and contracting problem is
\begin{equation}\hat{\mathcal{V}}_i(x_i, t;\, \eta_{i+1}) = \sup \limits_{I_{i+1} \in \hat{\mathcal{I}}} \sup \limits_{\eta_i \ge 0} \, \inf \limits_{\phi_i \in \Phi} \; \mathbb{E}^{\phi_i}_{x_i, t} \bigg( \hat X_i(\tau) + \dfrac{\tau - t}{2\varepsilon_i}\ \int_0^\infty \phi_i^2(z) \, \nu(\mathrm{d} z) \, \bigg| \, \tau > t \bigg),\end{equation}
Finally, the terminal reinsurer’s robust optimal contracting problem is
\begin{equation}\hat{V}_n(x_n, t) = \sup \limits_{\eta_n \ge 0} \, \inf \limits_{\phi_n \in \Phi} \; \mathbb{E}^{\phi_n}_{x_n, t} \bigg( \hat X_n(\tau) + \dfrac{\tau - t}{2\varepsilon_n}\ \int_0^\infty \phi_n^2(z) \, \nu(\mathrm{d} z) \, \bigg| \, \tau > t \bigg).\end{equation}
Next, we define equilibrium for n linked Stackelberg games under the chain structure.
Definition 4.1 (Stackelberg equilibrium under the chain structure). The Stackelberg equilibrium of the reinsurance chain is the following collection of controls:
$\hat \eta_n \in \mathcal{P}$
, which achieves the supremum in (4.4);
$\hat \phi_n = \phi_n(\cdot \, ;\, \hat \eta_n) \in \Phi$
, which achieves the infimum in (4.4). For
$i=1,2,\dots,n-1$
,
$\hat I_{i+1} = \hat I_{i+1}(\cdot \, ;\, \hat \eta_{i+1}) \in \hat{\mathcal{I}}$
, which achieves the outer supremum in (4.3);
$\hat \eta_i = \hat \eta_i(\cdot \,;\, \hat I_{i+1}, \hat \eta_{i+1}) \in \mathcal{P}$
, which achieves the inner supremum in (4.3);
$\hat \phi_i = \hat \phi_i(\cdot \, ;\, \hat I_{i+1}, \hat \eta_i, \hat\eta_{i+1}) \in \Phi$
, which achieves the infimum in (4.3).
$\hat I_1 = \hat I_1(\cdot\,;\, \hat\eta_1)\in \hat{\mathcal{I}}$
, which achieves the supremum in (4.2);
$\hat \phi_0 = \hat\phi_0(\cdot \, ;\, \hat I_1, \hat \eta_1) \in \Phi$
, which achieves the infimum in (4.2). We also define the insurer’s equilibrium value function by
$\hat V_0(x_0, t) \,:\!=\, \hat{\mathcal{V}}(x_0, t;\, \hat \eta_1)$
and intermediate reinsurer i’s equilibrium value function by
$\hat V_i(x_i, t) = \hat{\mathcal{V}}_i(x_i, t;\, \hat \eta_{i+1})$
for
$i = 1, 2, \dots, n-1$
.
Although Cao et al. (Reference Cao, Li, Young and Zou2022b) study a similar chain structure in which all reinsurers adopt a generalized mean-variance premium principle, the work in this section is not a special case of that paper because, in equilibrium, the generalized mean-variance principle reduces to a generalized expected-value principle with the loading on the variance identically zero. By contrast, the variance loading in this paper is nonzero in equilibrium because the expected-value loading is forced to be zero. We also considered Stackelberg reinsurance games under the chain structure in Cao et al. (Reference Cao, Li, Young and Zou2023a); the market therein consists of two reinsurers, one applying the expected-value premium principle and the other adopting the variance premium principle. By comparison, there are n reinsurers in this paper, and all of them apply the same variance premium principle (with differing loadings on the variance in equilibrium).
We compute the Stackelberg equilibrium under the chain structure in Theorem 4.1 below; see Appendix B.1 for its proof. Define
\begin{equation}\beta_i = \dfrac{\frac{1}{\varepsilon_i}}{ \sum_{j=0}^i \frac{1}{\varepsilon_j}},\end{equation}
for
$i =0, 1, 2, \dots, n$
. We will frequently use the fact that
$1-\beta_i = \frac{\varepsilon_i\beta_i}{\varepsilon_{i-1}\beta_{i-1}}$
.
Theorem 4.1. The equilibrium controls for all players in the Stackelberg reinsurance chain are given by the following expressions:
-
1. Equilibrium indemnity: if we define
$\hat{I}_{n+1} \equiv 0$
, then
$\hat{I}_i$
satisfies recursion: (4.6)for
\begin{equation}\hat{I}_i(z) = \dfrac{\beta_i}{2^i} \, z + \frac{\varepsilon_i\beta_i}{\varepsilon_{i-1}\beta_{i-1}} \, \hat{I}_{i+1}(z),\end{equation}
$i = 1, 2, \dots, n$
, or equivalently, (4.7)
\begin{equation}\hat{I}_i(z) = \frac{1}{\varepsilon_{i-1}\beta_{i-1}}\sum_{j=i}^n \dfrac{\varepsilon_{j-1}\beta_{j-1}\beta_j}{2^j} \, z.\end{equation}
-
2. Equilibrium premium loadings:
and for
\[\hat{\eta}_n = 2\varepsilon_n + \varepsilon_{n-1}\beta_{n-1} = \varepsilon_n \, \dfrac{2 - \beta_n}{1 - \beta_n},\]
$i = 1, 2, \dots, n-1$
, (4.8)or equivalently,
\begin{equation} \hat{\eta}_i = \dfrac{\varepsilon_{i-1}\beta_{i-1}}{\varepsilon_i + \hat{\eta}_{i+1}} \left\{\varepsilon_i + \left(\dfrac{2}{\beta_i} - 1 \right) \hat{\eta}_{i+1} \right\}, \end{equation}
(4.9)
\begin{equation} \hat{\eta}_i = \varepsilon_{i-1}\beta_{i-1}\, \left\{ \dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^{i-1}\sum_{j=i}^n \frac{\varepsilon_{j-1}\beta_{j-1}\beta_j}{2^j}} -1\right\}. \end{equation}
-
3. Equilibrium probability distortions: if we define
$\hat{\phi}_{n+1}(z) = \frac{\varepsilon_n\beta_n}{2^{n+1}}z$
, then (4.10)for
\begin{equation}\hat{\phi}_i(z) = \dfrac{\varepsilon_i\beta_i}{2^{i+1}} \, z + \hat{\phi}_{i+1}(z),\end{equation}
$i =0, 1, 2, \dots, n$
, or equivalently, (4.11)
\begin{equation}\hat{\phi}_i(z) = \left\{ \sum_{j=i}^n \dfrac{\varepsilon_j\beta_j}{2^{j+1}} + \dfrac{\varepsilon_n\beta_n}{2^{n+1}} \right\} z.\end{equation}
-
4. Equilibrium value function:
(4.12)in which
\begin{equation}\hat V_i(x_i, t) = x_i + \int_0^\infty \mathfrak{p}_i(z) \nu(\mathrm{d} z) \cdot \mathbb{E}( \tau - t | \tau >t),\end{equation}
(4.13)
\begin{equation}\mathfrak{p}_i(z) = \begin{cases} c - z - \dfrac{\hat{\phi}_0(z)}{2} \, z, &\quad i = 0, \\[9pt] \dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^{i+1}}\, \hat{I}_i(z)z = \dfrac{1}{2^{i+1}} \left(\dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^i} \, z - \hat{\phi}_i(z) \right) z, &\quad i = 1, 2, \dots, n. \end{cases}\end{equation}
In the following, we study the effect of reordering two “neighboring” reinsurers in the chain, which will help us determine the optimal chain structure. Consider two reinsurance chains, which we call chain 1 and chain 2. The ambiguity aversions in chain 1 are labeled by
$\varepsilon_{1,i}$
,
$i = 0, 1, \dots, n$
. We obtain chain 2, whose ambiguity aversions are labeled by
$\varepsilon_{2,i}$
, by switching the order of reinsurer k and reinsurer
$k+1$
in chain 1 for some
$k = 1, 2, \dots, n-1$
. Specifically,
\[\varepsilon_{1,k} = \varepsilon_{2, k+1}, \qquad \varepsilon_{1,k+1} = \varepsilon_{2,k}, \qquad \varepsilon_{1,i} = \varepsilon_{2,i}, \quad i \neq k, k+1.\]
We label the equilibrium controls and value functions similarly. For example,
$\hat V_{1,i}$
and
$\hat V_{2,i}$
denote the equilibrium value functions for player i in chain 1 and chain 2, respectively. The next proposition presents the effect of switching two reinsurers; see Appendix B.2 for its proof.
Proposition 4.1. The following statements are equivalent:
-
1.
$\varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}$
. -
2.
$\hat{\phi}_{1,i}(z) < \hat{\phi}_{2,i}(z)$
for
$i = 0, 1, \dots, k$
and
$z>0$
. -
3.
$\hat V_{1,i} > \hat V_{2,i}$
for
$i = 0, 1, \dots, k$
. -
4.
$\hat V_{1,k+1} < \hat V_{2,k+1}$
. -
5.
$\sum_{i =0}^n \hat V_{1,i} > \sum_{i = 0}^n \hat V_{2,i}.$
Moreover,
$\hat{\phi}_{1,i} = \hat{\phi}_{2,i}$
for
$i = k+1, \dots, n$
, and
$\hat V_{1,i} = \hat V_{2,i}$
for
$i = k+2, \dots, n$
.
When
$\varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}$
, player
$k-1$
in chain 2 purchases reinsurance from reinsurer k with a higher level of ambiguity aversion, compared to reinsurer k in chain 1. From (4.11), an increase in the ambiguity aversion of any player increases player i’s ambiguity
$\hat{\phi}_i$
about the Poisson random measure N for all i; thus, one expects
$\hat{\phi}_{2,k} > \hat{\phi}_{1,k}$
. This effect induces player
$k-1$
and thereby all previous players in chain 2 to adjust their ambiguity about N upward, which results in lower value functions in equilibrium. Reinsurer
$k+1$
in chain 2 has a lower ambiguity aversion but faces a customer with a higher ambiguity aversion. The combining effect on the ambiguity
$\hat{\phi}_{k+1}$
is, however, neutralized, that is,
$\hat{\phi}_{1,k+1} = \hat{\phi}_{2,k+1}$
, but the value function is increased. The results above are consistent with Proposition 4.1 in Cao et al. (Reference Cao, Li, Young and Zou2022b), in which the authors study a reinsurance chain with all reinsurers adopting the mean-variance premium principle.
The impact on reinsurer i, for
$i =k+1, \dots, n$
, depends on the premium rule adopted. Under the mean-variance premium principle, Cao et al. (Reference Cao, Li, Young and Zou2022b) show that these reinsurers in chain 2 will have a smaller ambiguity
$\phi$
and larger value functions because the switching decreases their “effective” ambiguity aversions. However, if variance premium rule is adopted, these reinsurers are indifferent before and after the switching.
In the following theorem, we allow each ceding (re)insurer to choose its accepting reinsurer in order to maximize its value function, while fixing the primary insurer, which introduces an additional choice within the linked Stackelberg games. More specifically, the primary insurer chooses a reinsurer among the set of n reinsurers. That chosen reinsurer becomes player 1; then, player 1 chooses a reinsurer among the set of
$n-1$
remaining reinsurers, and so on, until only one reinsurer remains, and that last one is the terminal reinsurer, or player n. Note that reinsurer i only has
$n-i$
reinsurers from which to choose. The next theorem determines the equilibrium order under this expanded Stackelberg game.
Theorem 4.2. The equilibrium order under the expanded Stackelberg game, in which each ceding (re)insurer chooses its accepting reinsurer from the pool of remaining reinsurers, is the one for which the ambiguity parameters are in increasing order, that is,
\begin{equation}\varepsilon_1 < \varepsilon_2 < \cdots < \varepsilon_n.\end{equation}
Proof. By Proposition 4.1, the primary insurer’s value function increases each time we switch two adjacent reinsurers so that their ambiguity aversions are in increasing order. Therefore, the order in (4.14) maximizes the value function of the primary insurer. The primary insurer only selects reinsurer 1, but
$\varepsilon_2 < \varepsilon_3 < \cdots \varepsilon_n$
also maximizes the value function of reinsurer 1 by Proposition 4.1. By continuing this argument, we deduce that all the ceding (re)insurers choose their accepting reinsurer in accordance with the order in (4.14).
The optimal structure in Theorem 4.2 is consistent with the one in Cao et al. (Reference Cao, Li, Young and Zou2022b), when all reinsurers adopt the mean-variance premium principle. In the next theorem, we evaluate which reinsurance structure – the tree or chain – maximizes the primary insurer’s objective function, because the primary insurer drives the initial demand for reinsurance by either buying from one reinsurer or from many. Please see Appendix B.3 for the proof of the theorem.
Theorem 4.3.
The primary insurer always prefers the tree over the chain. More specifically, for any
$x_0 \in \mathbb{R}$
and
$t \ge 0$
,
\[V_0(x_0, t) > \hat V_0(x_0, t).\]
Theorem 4.3 is consistent with our intuition, as well as with the remarks at the end of Section 3 that competition among reinsurers is better for the primary insurer. In the tree structure, the primary insurer negotiates reinsurance contracts with all reinsurers simultaneously. As a result, the indemnity purchased from one reinsurer depends on premiums offered by other reinsurers. Meanwhile, when setting the premium rate, the reinsurer also needs to take into account the premium loadings offered by its competitors. By contrast, in the chain structure, the primary insurer is only allowed to buy from one reinsurer, and there’s no competition embedded in the chain. Theorem 4.3 tells us that the tree structure always provides a higher value to the primary insurer, even compared to the optimal chain structure; recall that, for the tree structure, the order of ambiguity aversion does not matter, that is, there is no particular order to the reinsurers.
It is also interesting to notice that the premium rules adopted by reinsurers affect the primary insurer’s preference over different structures. When the game involves two reinsurers – one adopting the expected-value premium principle and the other, the variance premium principle – Cao et al. (Reference Cao, Li, Young and Zou2022b) show that there is no definite preference between tree and chain (in this case, there are two chains to consider due to two different premium rules). However, when all reinsurers adopt the variance premium principle, the primary insurer always prefers the tree over the chain.
5. Conclusions
We applied a game approach to study dynamic reinsurance contracting and competition problems, with the former modeled by Stackelberg differential games and the latter modeled by a non-cooperative Nash game. The reinsurance market in Section 2 consists of one insurer and n (
$n \ge 2$
) competing reinsurers, who all apply the same variance premium principle, with possibly different loadings, and who are distinguished by their ambiguity aversion levels. First, we considered the tree structure, in which the insurer negotiates reinsurance with all n reinsurers simultaneously, and we derived equilibrium strategies for all companies in (semi-)closed form. We showed that, in equilibrium, the insurer purchases a positive amount of proportional reinsurance from each reinsurer. The insurer benefits from an increasing number of competing reinsurers because it cedes a larger portion of risk in equilibrium, and its ambiguity penalty is consequently lowered. In Section 4, we considered the same
$n+1$
players in a chain structure, in which the risk of the insurer is shared sequentially among all n reinsurers, and showed that, from the perspective of the insurer, the tree structure is always preferred to the chain structure because the former requires full competition among the reinsurers (Theorem 4.3).
For future work, we will determine if Theorem 4.3 holds in other settings. For example, Chen et al. (Reference Chen, Shen and Su2020) study the chain structure under the mean-variance criterion with reinsurers who apply the variance principle. We will consider the tree structure in the same setting and compare our results to Chen et al. (Reference Chen, Shen and Su2020) to see if Theorem 4.3 holds under the mean-variance criterion, as it does for the mean-ambiguity criterion of this paper.
Furthermore, we plan to consider more general structures, such as multiple levels of reinsurers that compete at each level. The tree and chain structures are two special cases of such a general structure. In fact, one can view them as extreme special cases, with the tree embodying full competition among the reinsurers and the chain embodying monopolistic relationships. Under the mean-ambiguity criterion with each reinsurer adopting the variance premium principle, we anticipate that the insurer will prefer the tree over any other structure.
Acknowledgments
We are grateful to three anonymous reviewers for their insightful comments. Jingyi Cao and Dongchen Li acknowledge the financial support from the Natural Sciences and Engineering Research Council of Canada (grant numbers 05061 and 04958, respectively).
Competing interest
None.
A. Proofs of Section 3
A.1. Proof of Theorem 3.1
In this appendix, we apply the Hamilton–Jacobi–Bellman–Issac (HJBI) equation method to solve the insurer’s problem in (2.6); see Mataramvura and Øksendal (Reference Mataramvura and Øksendal2008) for a standard reference. We start by defining an integro-differential operator
$\mathcal{A}_0^{(I, \phi_0)}$
for the insurer. Given positive premium loadings
$\vec{\eta} = (\eta_1, \eta_2, \dots, \eta_n)$
, for any collection of indemnities
$I = (I_1, I_2, \dots, I_n) \in \mathcal{I}$
and for any probability distortion
$\phi_0 \in \Phi$
, define
$\mathcal{A}_0^{(I, \phi_0)}$
by:
\begin{align*}\mathcal{A}_0^{(I, \phi_0)} f &= \partial_t f + \left\{ c - \int_0^\infty \left\{ \sum_{i=1}^n I_i(z) + \sum_{i=1}^n \frac{\eta_i}{2} \, I_i^2(z) \right\} \nu(\mathrm{d} z)\right\} \partial_{x_0} f \notag\\&\quad + \int_{0}^{\infty} \left\{ f \bigg(x_0 - \bigg(z - \sum_{i=1}^n I_i(z) \bigg), t \bigg) - f(x_0, t) \right\} (1 + \phi_0(z)) \nu(\mathrm{d} z),\end{align*}
in which
$f \in \mathcal{C}^{1, 1}(\mathbb{R} \times \mathbb{R}_+)$
, and
$\partial_t f$
and
$\partial_{x_0} f$
denote the partial derivatives of f with respect to t and
$x_0$
, respectively. In writing
$\mathcal{A}_0^{(I_0, \phi_0)}$
, we suppress the dependence of the operator on
$\vec{\eta}$
.
Proof of Theorem 3.1. Based on a verification lemma similar to Lemma 3.1 in Cao et al. (Reference Cao, Li, Young and Zou2022a), suitably modified for the variance premium principle, if we find a smooth function that satisfies the following HJBI equation, subject to a transversality condition (see (A.4) below):
\begin{align}\sup\limits_{I \in \mathcal{I}} \, \inf \limits_{\phi_0 \in \Phi} \left\{\mathcal{A}_0^{(I, \phi_0)} V(x_0, t;\, \vec{\eta}) + \dfrac{1}{2\varepsilon_0} \int_0^\infty \phi_0^2(z) \nu(\mathrm{d} z) \right\} = \rho(t) \big(V(x_0, t;\, \vec{\eta}) - x_0 \big), \hspace{2em}\end{align}
then that solution equals the insurer’s value function
$\mathcal{V}_0$
defined by (2.6). In (A.1),
$\rho(t)$
is the deterministic hazard rate of the random horizon
$\tau$
, as defined in (2.5). To solve (A.1), we consider an ansatz
$\mathcal{V}(x_0, t;\, \vec{\eta}) = x_0 + v_0(t;\, \vec{\eta})$
, in which
$v_0$
is yet to be determined. By substituting the ansatz into (A.1), we obtain
\begin{align}v_0'(t) + c - \rho(t) v_0(t) = \inf\limits_{I} \sup \limits_{\phi_0} &\bigg[ \int_0^\infty \left\{ \sum_{i=1}^n \left(I_i + \dfrac{\eta_i}{2} \, I_i^2 \right) \right\} \nu(\mathrm{d} z) \\&\;\; + \int_0^\infty \left(z - \sum_{i=1}^n I_i \right)(1 + \phi_0) \, \nu(\mathrm{d} z) - \dfrac{1}{2\varepsilon_0} \int_0^\infty \phi_0^2 \, \nu(\mathrm{d} z) \bigg]. \notag\end{align}
We first solve the inner maximization problem over
$\phi_0$
and obtain the optimal distortion
$\phi_0^*(z;\, I, \vec{\eta})$
as stated in (3.1). Next, by substituting (3.1) into (A.2), the outer minimization problem over I is equivalent to minimizing
\begin{align}\mathfrak{f}(I_1, I_2, \dots, I_n) \,:\!=\, \sum_{i=1}^n \dfrac{\eta_i}{2} \, I_i^2 +\dfrac{\varepsilon_0}{2}\left(z - \sum_{i=1}^n I_i \right)^2.\end{align}
A straightforward calculation shows that
$I_i^*(z;\, \vec{\eta})$
in (3.2) is the unique minimizer of the above
$\mathfrak{f}$
. We directly see
$I^*_i(z;\, \vec{\eta}) > 0$
for all i and
$\sum_{i=1}^n I^*_i(z;\, \vec{\eta}) <z$
for all
$z > 0$
, which implies
$I^*(z;\, \vec{\eta}) = (I^*_1(z;\, \vec{\eta}), I^*_2(z;\, \vec{\eta}), \dots, I^*_n(z;\, \vec{\eta})) \in\mathcal{I}$
.
Lastly, substituting
$\phi^*_0(z;\, \vec{\eta})$
and
$I^*(z;\, \vec{\eta})$
into (A.2) yields
\begin{align*}v_0'(t) + c-\rho(t) v_0(t) = \int_0^\infty \left\{ \sum_{i=1}^n \dfrac{\eta_i}{2} \, (I^*_i(z))^2 + z + \dfrac{\varepsilon_0}{2} \left(z - \sum_{i=1}^n I^*_i \right)^2 \right\} \nu(\mathrm{d} z),\end{align*}
the solution to which, subject to the transversality condition:
\begin{equation}\lim_{s \to \infty}\mathbb{E}^{\phi_0}_{x_0, t} \Big[ \mathrm{e}^{-\int_t^s \rho(u) \mathrm{d} u} \, \mathcal{V}_0(X_0(s), s;\, \vec{\eta}) \Big] = 0,\end{equation}
is given by
\begin{align*}v_0(t;\, \vec{\eta}) = \left( c - \int_0^\infty \left\{ z + \sum_{i=1}^n\dfrac{\eta_i}{2} \, \big(I^*_i(z;\,\vec{\eta}) \big)^2 + \dfrac{\varepsilon_0}{2} \, \left(z - \sum_{i=1}^n I^*_i(z;\,\vec{\eta}) \right)^2 \right\} \nu(\mathrm{d} z) \right) \cdot \mathbb{E}(\tau - t|\tau > t). \end{align*}
Thus, the value function of the insurer equals
$\mathcal{V}(x_0, t;\, \vec{\eta}) = x_0 + v_0(t;\, \vec{\eta})$
, with the optimal controls as stated.
In the above analysis, we assume that
$\eta_i > 0$
for all
$i=1,2,\dots,n$
(or equivalently,
$\prod_{i=1}^{n} \, \eta_i > 0$
), which we use to find the minimizer of
$\mathfrak{f}$
in (A.3); see the paragraph following the statement of Theorem 3.1 for a detailed discussion about this assumption. In the rest of this appendix, we relax this assumption and consider the case in which some
$\eta_i$
is allowed to equal 0 (or equivalently,
$\prod_{i=1}^{n} \, \eta_i = 0$
). Define
$S_0 \,:\!=\, \{i \,:\, \eta_i = 0\}$
to mark those reinsurers whose premium loadings equal 0. Then, the function
$\mathfrak{f}$
in (A.3) equals
\[\mathfrak{f}(I_1, I_2, \dots, I_n) = \sum_{i \notin S_0}\frac{\eta_i}{2} \, I_i(z;\, \vec{\eta})^2 + \frac{\varepsilon_0}{2}\left(z - \sum_{i\in S_0} I_i (z;\, \vec{\eta}) - \sum_{i \notin S_0} I_i (z;\, \vec{\eta}) \right)^2.\]
Minimizing the above
$\mathfrak{f}$
then yields the optimal indemnity
$I^*_i(z;\,\vec{\eta})$
, for
$i=1,2,\dots,n$
: when
$\prod_{i=1}^{n} \, \eta_i = 0$
,
\begin{equation}I^*_i(z;\,\vec{\eta}) =\begin{cases}0, &\quad i \notin S_0, \\\text{any nonnegative value } s.t.\ \sum_{i \in S_0}I^*_i(z;\,\vec{\eta}) =z, &\quad i \in S_0.\end{cases}\end{equation}
A.2. Proof of Theorem 3.2
In this appendix, we solve reinsurer i’s problem in (2.7). The HJBI equation method used in Appendix A.1 is applicable here, with only minor changes. Given positive premium loadings
$\vec{\eta}$
and for a probability distortion
$\phi_i \in \Phi$
, define the integro-differential operator
$\mathcal{A}_i^{(\vec{\eta}, \phi_i)}$
for reinsurer i by
\begin{align*} \mathcal{A}_i^{(\vec{\eta}, \phi_i)} f &= \partial_t f + \int_0^\infty \left\{ I^*_i(z;\, \vec{\eta}) + \dfrac{\eta_i}{2}(I^*_i)^2 (z;\, \vec{\eta}) \right\} \nu(\mathrm{d} z) \cdot \partial_{x_i} f \notag\\ &\quad + \int_0^\infty \big\{f(x_i - I^*_i(z;\, \vec{\eta}), t) - f(x_i, t)\big\} (1 + \phi_i(z)) \nu(\mathrm{d} z),\end{align*}
in which
$f \in \mathcal{C}^{1, 1}(\mathbb{R} \times \mathbb{R}_+)$
and
$I^*_i(z;\, \vec{\eta})$
is given by (3.2), for
$i=1,2,\dots,n$
.
Proof of Theorem 3.2. Based on a verification lemma similar to Lemma 3.2 in Cao et al. (Reference Cao, Li, Young and Zou2022a), suitably modified for the variance premium principle, if we find a smooth function that satisfies the following HJBI equation, subject to a transversality condition (as in (A.4)):
\begin{equation}\sup\limits_{\eta_i > 0} \inf\limits_{\phi_i \in \Phi} \left\{\mathcal{A}_i^{(\vec{\eta}, \phi_i)} \mathcal{V}_i(x_i, t;\, \vec{\eta}_{(i)}) + \dfrac{1}{2\varepsilon_i} \int_0^\infty \phi_i^2(z) \nu(\mathrm{d} z) \right\} = \rho(t)\left(\mathcal{V}_i(x_i, t;\, \vec{\eta}_{(i)}) - x_i\right).\end{equation}
then that solution equals the value function
$\mathcal{V}_i$
defined in (2.7). We consider an ansatz in the form of
$\mathcal{V}(x_i, t;\, \vec{\eta}_{(i)}) = x_i + v_i(t;\, \vec{\eta}_{(i)})$
and insert it into (A.6) to obtain
\begin{equation}v_i'(t) + \sup_{\eta_i} \inf_{\phi_i} \int_0^\infty \left\{ \frac{\eta_i}{2} (I^*_i(z;\, \vec{\eta}))^2 - \phi_i I^*_i(z;\, \vec{\eta}) + \dfrac{\phi_i^2}{2 \varepsilon_i} \right\} \nu(\mathrm{d} z) = \rho(t) v_i(t).\end{equation}
Minimizing the above integrand over
$\phi_i$
yields the optimal distortion
$\phi^*_i(z;\, \vec{\eta})$
as stated in (3.3), which helps us simplify (A.7) to
\begin{equation}v_i'(t) + \sup_{\eta_i} \int_0^\infty \left\{ \dfrac{\eta_i - \varepsilon_i}{2}\, (I^*_i(z;\, \vec{\eta}))^2 \right\} \nu(\mathrm{d} z) = \rho(t) v_i(t).\end{equation}
By recalling
$I^*_i(z;\, \vec{\eta})$
from (3.2), the first-order condition of the above maximization problem for
$\eta_i$
is
\begin{align} 2 \left(1 - \frac{\varepsilon_i}{\eta_i} \right) \bigg(1 + \sum_{j \neq i} \frac{\varepsilon_0}{\eta_j} \bigg) = 1 + \sum_{j = 1}^n \frac{\varepsilon_0}{\eta_j},\end{align}
from which we obtain the optimal premium loading
$\bar{\eta}_i(\vec{\eta}_{(i)})$
, as stated in (3.4).
Let
$\vec{\eta}'$
denote the collection of premium loadings that is obtained from
$\vec{\eta}$
by replacing
$\eta_i$
with
$\bar{\eta}_i(\vec{\eta}_{(i)})$
. By substituting
$\bar{\eta}_i(\vec{\eta}_{(i)})$
and
$\phi^*_i(z;\, \vec{\eta}')$
into (A.6), we obtain a first-order differential equation for
$v_i(t;\, \vec{\eta}_{(i)})$
, which is easily solved when we apply the required transversality condition, as in (A.4). Thus, we have proved Theorem 3.2.
Thus far, we have solved the reinsurer’s problem in (2.7) when all premium loadings are positive, or equivalently,
$\prod_{i=1}^n \, \eta_i > 0$
. (The same assumption is also imposed in Theorem 3.1 to study the insurer’s problem.) The proposition below implies that such an assumption does not impose any restriction to the analysis.
Proposition A.1. It is never optimal for a reinsurer to offer a reinsurance contract with zero premium loading.
Proof. Fix an arbitrarily chosen reinsurer
$i = 1, 2, \dots, n$
. We have shown that, when
$\prod_{j=1}^n \, \eta_j > 0$
, the reinsurer i’s optimal loading
$\bar{\eta}_i(\vec{\eta}_{(i)})$
given by (3.4) is indeed positive. Thus, we focus on the case for which
$\prod_{j=1}^n \, \eta_j = 0$
in the rest of the proof. First, observe that, when
$\prod_{i=1}^n \, \eta_i =0$
, the reinsurer i’s optimal premium loading is still solved from the same maximization problem in (A.8), but now with
$I^*_i(z;\, \vec{\eta})$
given by (A.5). To proceed, we consider the following two scenarios:
-
(1) First, suppose all other reinsurers offer positive premium loadings, that is,
$\prod_{j\neq i}\eta_j >0$
: if reinsurer i were to offer
$\eta_i=0$
, then by (A.5),
$I^*_i = z$
and the integrand in (A.8) would be strictly negative. Therefore, any
$\eta_i > \varepsilon_i$
is preferred to
$\eta_i = 0$
. -
(2) Second, suppose there exists a reinsurer j,
$j\neq i$
, such that
$\eta_j=0$
, that is,
$\prod_{j\neq i}\eta_j =0$
: if reinsurer i were to offer
$\eta_i > 0$
, then the insurer would never purchase reinsurance from reinsurer i, that is,
$I^*_i =0$
, and the integral in (A.8) would be identically zero. However, if reinsurer i were to offer
$\eta_i =0$
, then the insurer might purchase
$I^*_i > 0$
, which would make the integral in (A.8) strictly negative, making
$\eta_i =0$
a non-optimal choice for reinsurer i.
The desired result follows because the above two scenarios are exhaustive.
A.3. Proof of Theorem 3.3
For any collection of positive premium loadings, we define
\begin{align*} y_i = \frac{1}{\eta_i}, \text{ for } i=1,2,\dots,n, \quad \text{ and } \quad \alpha = \sum_{i=1}^n \, y_i.\end{align*}
From the proof of Theorem 3.2, we know that the optimal loadings are obtained from (A.9), which can be rewritten as:
\begin{align*} 2(1-\varepsilon_i y_i) \big(1 + \varepsilon_0( \alpha - y_i)\big) = 1+\varepsilon_0\alpha.\end{align*}
Solving the above quadratic equation yields two solutions and only one of them is less than
$\alpha$
, as required, which is given by:
\begin{align*} y_i = \dfrac{\varepsilon_0 + \varepsilon_i(1 + \varepsilon_0\alpha) - \sqrt{\Delta_i(\alpha)}}{2\varepsilon_0\varepsilon_i},\end{align*}
in which
$\Delta_i(\alpha) = \varepsilon_0^2 + \varepsilon_i^2(1 + \varepsilon_0\alpha)^2 > \varepsilon_i^2\varepsilon_0^2\alpha^2$
. By taking the sum of
$y_i$
over i, and by the definition of
$\alpha$
, we show that such an
$\alpha$
, if exists, is a positive zero of the function
$\mathfrak{h}$
defined in (3.6).
Next, we show that
$\mathfrak{h}(\alpha) = 0$
has a unique positive solution, denoted by
$\alpha^*$
. First,
\begin{align*} \lim_{\alpha \to 0^+} \mathfrak{h}(\alpha) = \frac{n}{2 \varepsilon_0} + \frac{1}{2} \sum_{i=1}^n \, \left(\frac{1}{\varepsilon_i} - \sqrt{\frac{1}{\varepsilon_i^2} + \frac{1}{\varepsilon_0^2} }\right) > 0\end{align*}
and, for
$\alpha$
sufficiently large,
$\mathfrak{h}(\alpha)< 0$
. These boundary conditions, together with the continuity of
$\mathfrak{h}$
over
$(0, \infty)$
, imply there exists a positive zero of
$\mathfrak{h}$
. A straightforward calculation yields
\begin{align*} \mathfrak{h}'(\alpha) &= \frac{n-2}{2} - \frac{1}{2} \sum_{i=1}^n \frac{\frac{1}{\varepsilon_0} + \alpha}{\sqrt{\frac{1}{\varepsilon_i^2} + \left(\frac{1}{\varepsilon_0} + \alpha \right)^2 }},\end{align*}
in which the last term is an increasing function of
$\alpha$
. Thus, one of the following two statements must be true: (1)
$\mathfrak{h}'(\alpha) \le 0$
for all
$\alpha > 0$
; or (2) there exists a
$\alpha_0 \in (0, \infty)$
such that
$\mathfrak{h}'(\alpha)\ge 0$
for all
$ 0 < \alpha \le \alpha_0$
and
$\mathfrak{h}'(\alpha)< 0$
for all
$ \alpha > \alpha_0$
. In either case,
$\mathfrak{h}(\alpha)$
, as a function of
$\alpha$
, only crosses the positive horizontal axis once.
With equilibrium loadings obtained in (3.5), the remaining results in Theorem 3.3 can be verified by straightforward computation, which we leave to the interested reader as an exercise.
B. Proofs of Section 4
B.1. Proof of Theorem 4.1
For ease of notation, define
$a_i = \sum_{j=0}^{i-1}\frac{1}{\varepsilon_j}$
, for
$i =1, 2, \dots, n$
.
(1) Primary insurer: Based on Lemma 3.1 and Theorem 3.1 of Cao et al. (Reference Cao, Li, Young and Zou2022a) (and their proofs), suitably modified for the variance premium principle, we know that the primary insurer solves the following problem, in which the primary insurer buys
$I_1$
from reinsurer 1 at a premium loading of
$\eta_1$
:
\begin{equation*}\sup_{I_1}\inf_{\phi_0} \bigg[ - I_1 - \dfrac{\eta_1}{2} I_1^2 - (z-I_1)\,(1+ \phi_0) + \dfrac{\phi_0^2}{2\varepsilon_0}\bigg],\end{equation*}
whose solution is
\[\hat{\phi}_0(z;\, I_1, \eta_1) = \varepsilon_0(z- I_1),\]
and
\begin{equation}\hat{I}_1(z;\, \eta_1) = \dfrac{\varepsilon_0}{\varepsilon_0 + \eta_1} \, z = \dfrac{1}{1 + a_1\eta_1} \, z.\end{equation}
(2) Intermediate reinsurer
i
,
$i =1, 2, \dots, n-1$
: Reinsurer i sells
$I_i$
to reinsurer
$i-1$
with a premium loading of
$\eta_i$
and purchases reinsurance
$I_{i+1}$
from the next player with a premium loading of
$\eta_{i+1}$
. Therefore, based on Lemma A.1 and Theorem 3.2 of Cao et al. (Reference Cao, Li, Young and Zou2022b), suitably modified for the variance premium principle, we know that intermediate reinsurer i solves the following problem, in which
$\hat{I}_i$
is the optimal choice of indemnity of reinsurer
$i-1$
:
\begin{align}&\sup_{I_{i+1}}\sup_{\eta_i} \inf_{\phi_i} \left[ \hat{I}_i+ \dfrac{\eta_i}{2}(\hat{I}_i)^2 - I_{i+1} - \dfrac{\eta_{i+1}}{2} \, I_{i+1}^2 - (\hat{I}_i - I_{i+1})(1+\phi_i) + \dfrac{\phi_i^2}{2\varepsilon_i} \right] \notag \\&= \sup_{I_{i+1}}\sup_{\eta_i} \left[ \dfrac{\eta_i}{2}(\hat{I}_i)^2 - \dfrac{\eta_{i+1}}{2} \, I_{i+1}^2 - \dfrac{\varepsilon_i}{2}(\hat{I}_i - I_{i+1})^2 \right] \notag \\&= \sup_{\eta_i} \sup_{I_{i+1}} \left[ \dfrac{\eta_i}{2}(\hat{I}_i)^2 - \dfrac{\eta_{i+1}}{2} \, I_{i+1}^2 - \dfrac{\varepsilon_i}{2}(\hat{I}_i - I_{i+1})^2 \right].\end{align}
The second line in (B.2) follows because the optimal distortion equals
$\hat{\phi}_i(z;\, \eta_i, I_{i+1}) = \varepsilon_i(\hat{I}_i - I_{i+1})$
.
For a given value of
$\eta_i$
, maximize the expression in (B.2) with respect to
$I_{i+1}$
and obtain the optimal
$\hat{I}_{i+1}$
in terms of
$\hat{I}_i$
as follows:
\begin{equation}\hat{I}_{i+1}(z;\, \hat{I}_i, \eta_i, \eta_{i+1}) = \dfrac{\varepsilon_i}{\varepsilon_i + \eta_{i+1}} \, \hat{I}_i(z;\, \eta_i).\end{equation}
Because
$\hat{I}_1$
in (B.1) is a constant multiple of z and because the
$\varepsilon_i$
and
$\eta_i$
are constants, (B.3) implies that
$\hat{I}_i$
is a constant multiple of z for all
$i = 1, 2, \dots, n$
. Thus, the expression in (B.2) is a constant multiple of
$z^2$
, and maximizing (B.2) over
$\eta_i$
is equivalent to maximizing it when
$z = 1$
. To that end, define the function
$\mathfrak{k}_i$
and simplify it as follows:
\begin{align*}\mathfrak{k}_i(\eta_i) &= \dfrac{\eta_i}{2}(\hat{I}_i)^2 - \dfrac{\eta_{i+1}}{2} \, (\hat{I}_{i+1})^2 - \dfrac{\varepsilon_i}{2}(\hat{I}_i -\hat{I}_{i+1})^2 \; \Big|_{z=1} \\&= \left\{ \dfrac{\eta_i}{2} - \dfrac{\eta_{i+1}}{2} \left( \dfrac{\varepsilon_i}{\varepsilon_i + \eta_{i+1}} \right)^2 - \dfrac{\varepsilon_i}{2} \left(\dfrac{\varepsilon_i}{\varepsilon_i + \eta_{i+1}} - 1 \right)^2 \right\} \big(\hat{I}_i(1) \big)^2 \\&= \left\{ \dfrac{\eta_i}{2} - \dfrac{1}{2} \cdot \dfrac{\varepsilon_i \eta_{i+1}}{\varepsilon_i + \eta_{i+1}} \right\} \big(\hat{I}_i(1) \big)^2.\end{align*}
Via induction, we will showFootnote 7
\begin{equation}\hat{I}_i(z;\, \eta_i) = \dfrac{1}{2^{i-1}(1 + a_i \eta_i)} \, z.\end{equation}
Under this assumption, the expression for
$\mathfrak{k}_i$
becomes
\begin{align*}\mathfrak{k}_i(\eta_i) &= \left\{ \dfrac{\eta_i}{2} - \dfrac{1}{2} \cdot \dfrac{\varepsilon_i \eta_{i+1}}{\varepsilon_i + \eta_{i+1}} \right\} \dfrac{1}{2^{2(i-1)}(1 + a_i \eta_i)^2}.\end{align*}
By maximizing
$\mathfrak{k}_i$
with respect to
$\eta_i$
, we obtain the optimal
$\hat{\eta}_i$
as a function of
$\eta_{i+1}$
:
\begin{equation}\hat{\eta}_i(\eta_{i+1}) = \dfrac{1}{a_i} + \dfrac{2\varepsilon_i \eta_{i+1}}{\varepsilon_i + \eta_{i+1}} = \varepsilon_{i-1} \beta_{i-1} + \dfrac{2\varepsilon_i \eta_{i+1}}{\varepsilon_i + \eta_{i+1}},\end{equation}
which one can show equals the recursion in (4.8). Furthermore, from (B.3) and (B.4), we obtain
\begin{align*}\hat{I}_{i+1}(z;\, \eta_{i+1}) &= \hat{I}_{i+1}(z;\, \hat{I}_i, \hat{\eta}_i, \eta_{i+1}) = \dfrac{\varepsilon_i}{\varepsilon_i + \eta_{i+1}} \, \hat{I}_i(z;\, \hat{\eta}_i) \\[2pt]&= \dfrac{\varepsilon_i}{\varepsilon_i + \eta_{i+1}} \cdot \dfrac{1}{2^{i-1}(1 + a_i \hat{\eta}_i(\eta_{i+1}))} \, z \\[2pt]&= \dfrac{1}{2^{i}(1 + a_{i+1} \eta_{i+1})} \, z,\end{align*}
in which the last line follows from the first expression for
$\hat{\eta}_i(\eta_{i+1})$
in (B.5) and from
$a_{i+1} = a_i + \frac{1}{\varepsilon_i}$
. Thus, we have proved (B.4) for all
$i = 1, 2, \dots, n$
.
Finally, the recursion for
$\hat{I}_i$
in (4.6) follows from (B.3), (B.4), and (B.5), and the recursion for
$\hat{\phi}_i$
in (4.10) follows from the recursion for
$\hat{I}_i$
.
(3) Terminal reinsurer
n
: Based on Lemma 3.2 and Theorem 3.2 of Cao et al. (Reference Cao, Li, Young and Zou2022a) and based on Theorem 3.3 of Cao et al. (Reference Cao, Li, Young and Zou2022b), suitably modified for the variance premium principle, we know that the terminal reinsurer solves the following problem, in which the terminal reinsurer n sells reinsurance
$\hat{I}_{n} = \frac{z}{2^{n-1}(1+a_n\eta_n)}$
to reinsurer
$n-1$
:
\[\sup_{\eta_n}\inf_{\phi_n} \bigg[ \hat{I}_n+ \dfrac{\eta_n}{2} \, (\hat{I}_n)^2 - \hat{I}_n(1+\phi_n) + \dfrac{\phi_n^2}{2\varepsilon_n}\bigg] = \sup_{\eta_n} \bigg[ \frac{\eta_n - \varepsilon_n}{2} \, (\hat{I}_n)^2\bigg] \,=\!:\, \sup_{\eta_n} \mathfrak{k}_n(\eta_n).\]
in which the optimal distortion is given by
$\hat{\phi}_n(z;\, \eta_n) = \varepsilon_n\hat{I}_n$
. Specifically,
\[\mathfrak{k}_n(\eta_n) = \dfrac{\eta_n - \varepsilon_n}{2} \cdot \dfrac{z^2}{2^{2(n-1)} (1+a_n\eta_n)^2},\]
which is maximized by:
\[\hat{\eta}_n = 2 \varepsilon_n + \dfrac{1}{a_n} = 2\varepsilon_n + \dfrac{1}{\sum_{j=0}^{n-1} \frac{1}{\varepsilon_j}}.\]
(4) Equilibrium: To compute the equilibrium, substitute
$\hat{\eta}_n$
into (B.4) with
$i = n$
to obtain
\[\hat{I}_n(z) = \dfrac{1}{2^{n-1}( 1 + 2a_n\varepsilon_n + 1)}z = \dfrac{1}{2^n(1+a_n\varepsilon_n)}z= \dfrac{\beta_n}{2^n} \, z,\]
and the recursions for
$\hat{I}_i$
,
$\hat{\eta}_i$
, and
$\hat{\phi}_i$
give us the explicit expressions in (4.7), (4.9), and (4.11), respectively.
(5) Equilibrium value function: Similar to the proof of Theorem 3.4 of Cao et al. (Reference Cao, Li, Young and Zou2022b), the value functions for the primary insurer (player 0) and reinsurer i, for
$i = 1, 2, \dots, n$
, are, respectively, given by:
\begin{equation}\hat V_0(x_0, t) = x_0 + \int_0^\infty \left(c - z - \dfrac{\hat{\eta}_1}{2}\hat{I}_1^2- (z- \hat{I}_1)\hat{\phi}_0 + \dfrac{\hat{\phi}_0^2}{2\varepsilon_0} \right) \nu(\mathrm{d} z) \cdot \mathbb{E}(\tau- t| \tau>t),\end{equation}
and
\begin{equation}\hat V_i(x_i, t) = x_i + \int_0^\infty \left( \dfrac{\hat{\eta}_i}{2} \, \hat{I}_i^2 - \dfrac{\hat{\eta}_{i+1}}{2} \, \hat{I}_{i+1}^2 - (\hat{I}_i - \hat{I}_{i+1}) \hat{\phi}_i + \dfrac{\hat{\phi}_i^2}{2\varepsilon_i} \right) \nu(\mathrm{d} z) \cdot \mathbb{E}(\tau - t| \tau >t),\end{equation}
in which we define
$\hat{I}_{n+1}\equiv 0$
.
Define
$\hat{I}_0 = z$
; then, (B.1) and (B.3) imply
\begin{equation*}\hat{\phi}_i = \varepsilon_i(\hat{I}_i - \hat{I}_{i+1}) = \varepsilon_i \, \dfrac{\hat{\eta}_{i+1}}{\varepsilon_i + \hat{\eta}_{i+1}} \, \hat{I}_i = \hat{\eta}_{i+1}\hat{I}_{i+1}, \qquad i = 0, 1, \dots, n-1,\end{equation*}
and
\[\hat{\phi}_n = \varepsilon_n \hat{I}_n.\]
Therefore, for
$i=0$
, the integrand in (B.6) equals
\[c - z - \dfrac{1}{2} \left(\hat{\phi}_0\hat{I}_1 + \dfrac{\hat{\phi}_0^2}{\varepsilon_0} \right) = c - z - \dfrac{1}{2} \left(\hat{\phi}_0 \left(z - \dfrac{\hat{\phi}_0}{\varepsilon_0} \right) + \dfrac{\hat{\phi}_0^2}{\varepsilon_0} \right) = c - z - \dfrac{\hat{\phi}_0}{2} \, z \,=\!:\, \mathfrak{p}_0(z),\]
and for
$i = 1, 2, \dots, n-1$
, the integrand in (B.7) equals
\begin{align*}\dfrac{1}{2} \left( \hat{\phi}_{i-1}\hat{I}_i - \hat{\phi}_i \hat{I}_{i+1} - \dfrac{\hat{\phi}_i^2}{\varepsilon_i} \right) &= \dfrac{1}{2} \left( \left(\dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^i}\, z + \hat{\phi}_i \right)\hat{I}_i - \hat{\phi}_i \hat{I}_{i+1} - \dfrac{\hat{\phi}_i^2}{\varepsilon_i} \right) \\&= \dfrac{1}{2} \left(\dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^i}\, \hat{I}_i \, z + \hat{\phi}_i(\hat{I}_i - \hat{I}_{i+1}) - \dfrac{\hat{\phi}_i^2}{\varepsilon_i} \right) \\&= \dfrac{\varepsilon_{i-1}\beta_{i-1}}{2^{i+1}} \, \hat{I}_i \, z \,=\!:\, \mathfrak{p}_i(z),\end{align*}
in which the first equality follows from (4.10). Also, from (4.6) we have
\[\hat{I}_i = \dfrac{\beta_i}{2^i} \,z + (1-\beta_i) \hat{I}_{i+1} = \dfrac{\beta_i}{2^i} \, z + (1-\beta_i) \left(\hat{I}_i - \dfrac{\hat{\phi}_i}{\varepsilon_i} \right),\]
which, together with
$\frac{\varepsilon_i\beta_i}{\varepsilon_{i-1}\beta_{i-1}} = 1 - \beta_i$
, implies
\[\hat{I}_i = \dfrac{z}{2^i} - \dfrac{\hat{\phi}_i}{\varepsilon_i} \cdot \dfrac{1 - \beta_i}{\beta_i} = \dfrac{z}{2^i} - \dfrac{\hat{\phi}_i}{\varepsilon_{i-1}\beta_{i-1}}.\]
One can verify the case when
$i = n$
similarly. Thus, we have proved Theorem 4.1.
B.2. Proof of Proposition 4.1
In this proof, we fix
$z>0$
.
Equivalence between 1 and 2: For
$i = k+1, \dots, n$
and
$j \ge i$
,
$ \varepsilon_j\beta_j = \frac{1}{\sum_{\ell=0}^j \frac{1}{\varepsilon_\ell}}$
is unaffected by switching
$\varepsilon_k$
and
$\varepsilon_{k+1}$
. Then, (4.11) implies
$\hat{\phi}_{1,i}(z) = \hat{\phi}_{2,i}(z)$
. For
$i =k$
, by recursion (4.10),
\[\hat{\phi}_k(z) = \dfrac{\varepsilon_k\beta_k}{2^{k+1}} \, z + \hat{\phi}_{k+1}(z),\]
in which
$\varepsilon_k\beta_k = \frac{1}{\sum_{\ell=0}^k \frac{1}{\varepsilon_\ell}}$
increases in
$\varepsilon_k$
. By comparing the two chains, because
$\hat{\phi}_{1,k+1}(z) = \hat{\phi}_{2,k+1}(z)$
, it follows that
$\hat{\phi}_{1,k}(z) < \hat{\phi}_{2,k}(z)$
if and only if
$\varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}$
. For
$i =0, 1, \dots, k-1$
, because
$\varepsilon_i\beta_i = \frac{1}{\sum_{\ell=0}^i \frac{1}{\varepsilon_\ell}}$
is unaffected by switching
$\varepsilon_k$
and
$\varepsilon_{k+1}$
, the recursion in (4.10) implies
$ \hat{\phi}_{1,i}(z) < \hat{\phi}_{2,i}(z)$
if and only if
$\hat{\phi}_{1,i+1}(z) < \hat{\phi}_{2,i+1}(z)$
, which is equivalent to
$\varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}$
.
Equivalence between 1 and 3: If
$i = 1, \dots, k$
, then
$\varepsilon_{i-1}\beta_{i-1}$
is the same for both chains 1 and 2. Thus, for
$i = 0, 1, \dots, k$
, (4.13) implies
\[\hat V_{1,i} > \hat V_{2,i} \iff \hat{\phi}_{1,i} < \hat{\phi}_{2,i} \iff \varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}.\]
Equivalence between 1 and 4: Recall
$\hat{\phi}_{1,k+1}(z) = \hat{\phi}_{2,k+1}(z)$
, and clearly
$\varepsilon_k\beta_k = \frac{1}{\sum_{\ell=0}^k \frac{1}{\varepsilon_\ell}}$
increases in
$\varepsilon_k$
. Then, (4.13) implies
$\hat V_{1,k+1} < \hat V_{2,k+1}$
if and only if
$\varepsilon_{1,k} < \varepsilon_{2,k} = \varepsilon_{1,k+1}$
.
Equivalence between 1 and 5: Without loss of generality, we set
$z = 1$
. Note that
$\hat V_{1,i} = \hat V_{2,i}$
for
$i = k+2, \cdots, n$
. We have
\begin{align*}\sum_{i = 0}^n \hat V_{1,i} - \sum_{i=0}^n \hat V_{2,i} & = \hat V_{1,0} - \hat V_{2,0} + \sum_{i=1}^k (\hat V_{1,i} - \hat V_{2,i}) + \hat V_{1, k+1} - \hat V_{2,k+1}\\& = \dfrac{1}{2}(\hat{\phi}_{2,0} - \hat{\phi}_{1,0}) + \sum_{i=1}^k \dfrac{1}{2^{i+1}}(\hat{\phi}_{2,i} - \hat{\phi}_{1,i}) + \dfrac{1}{2^{2k+3}}(\varepsilon_{1,k}\beta_{1,k} - \varepsilon_{2,k}\beta_{2,k})\\& = \dfrac{1}{2^{k+1}}\Big(\dfrac{1}{2} + \sum_{i=1}^k \dfrac{1}{2^{i+1}} - \dfrac{1}{2^{k+2}}\Big) \, \Big(\varepsilon_{2,k}\beta_{2,k} - \varepsilon_{1,k}\beta_{1,k}\Big) \\& = (1- \dfrac{3}{2^{k+2}})\, \Big( \dfrac{1}{ \sum_{l=0}^{k-1} \frac{1}{\varepsilon_{2,l}} + \frac{1}{\varepsilon_{2,k}}} - \dfrac{1}{ \sum_{l=0}^{k-1} \frac{1}{\varepsilon_{1,l}} + \frac{1}{\varepsilon_{1,k}}} \Big).\end{align*}
in which to go from the first to the second line, we used that fact that
$\varepsilon_{1,i-1} = \varepsilon_{2,i-1}$
for
$i = 1, 2, \cdots, k$
and
$\hat{\phi}_{1,k+1} = \hat{\phi}_{2, k+1}$
; and the third line is due to (4.11) and the fact that
$\varepsilon_{1,i}\beta_{1,i} = \varepsilon_{2,i}\beta_{2,i}$
for
$i \neq k$
. By noting the term in the first term is positive (
$k \ge 1$
), and
$\sum_{l=0}^{k-1} \frac{1}{\varepsilon_{2,l}} =\sum_{l=0}^{k-1} \frac{1}{\varepsilon_{1,l}}$
, the equation above is positive if and only if
$\varepsilon_{1,k} < \varepsilon_{2,k}$
.
B.3. Proof of Theorem 4.3
By comparing (3.8) and (3.9) with (4.12) and (4.13), we only need to show that for any
$z>0$
,
\begin{equation}c - z - \dfrac{\varepsilon_0}{2(1+\varepsilon_0 \alpha^*)} \, z^2 > c - z - \dfrac{\hat{\phi}_0(z)}{2} \, z.\end{equation}
Because
$\hat{\phi}_0(z)$
is proportional to z, in the following we let
$z = 1$
without loss of generality. Then (B.8) is equivalent to
$\alpha^* > \frac{1}{\hat{\phi}_0} - \frac{1}{\varepsilon_0}$
. Recall that
$\alpha^*$
is the unique zero of function
$\mathfrak{h}(\alpha)$
defined in (3.6) with
$\lim_{\alpha\to 0^+} \mathfrak{h}(\alpha) >0$
and
$\mathfrak{h}(\alpha) < 0$
for
$\alpha$
sufficiently large. Therefore,
$\alpha^* > \frac{1}{\hat{\phi}_0} - \frac{1}{\varepsilon_0}$
if and only if
$\mathfrak{h} \big(\frac{1}{\hat{\phi}_0} - \frac{1}{\varepsilon_0} \big) >0$
, which, with straightforward calculation, is equivalent to
\begin{equation}\dfrac{1}{2} \, \sum_{i=1}^n \Bigg( \dfrac{\hat{\phi}_0}{\varepsilon_i} + 1 - \sqrt{ \frac{\hat{\phi}_0^2}{\varepsilon_i^2}+1} \, \Bigg) > 1 - \dfrac{\hat{\phi}_0}{\varepsilon_0}.\end{equation}
For ease of notation, define
$\gamma_i = \dfrac{\varepsilon_0}{\varepsilon_i}$
for
$i = 1, 2, \dots, n$
. Then, according to (4.11) and (4.5), we have
\begin{equation}\dfrac{\hat{\phi}_0}{\varepsilon_0} = \dfrac{1}{2} + \sum_{i=1}^{n-1} \dfrac{1}{2^{i+1}} \, \dfrac{1}{1+\sum_{j=1}^i \gamma_j} + \dfrac{1}{2^n}\, \dfrac{1}{1+\sum_{j=1}^n \gamma_j},\end{equation}
which implies
\begin{equation}\begin{aligned} 1 - \dfrac{\hat{\phi}_0}{\varepsilon_0} &= \Bigg( \sum_{i=1}^{n-1}\dfrac{1}{2^{i+1}} + \dfrac{1}{2^n} \Bigg) - \sum_{i=1}^{n-1} \dfrac{1}{2^{i+1}}\, \dfrac{1}{1 + \sum_{j=1}^i \gamma_j} - \dfrac{1}{2^n}\, \dfrac{1}{1 + \sum_{j=1}^n \gamma_j} \\ &= \sum_{i=1}^{n-1}\dfrac{1}{2^{i+1}} \, \dfrac{\sum_{j=1}^i \gamma_j}{1+\sum_{j=1}^i \gamma_j} + \dfrac{1}{2^n}\, \dfrac{\sum_{j=1}^n \gamma_j}{ 1 + \sum_{j=1}^n \gamma_j}\\ & = \sum_{i=1}^n \gamma_i \Bigg( \underbrace{ \sum_{k=i}^{n-1} \dfrac{1}{2^{k+1}}\, \dfrac{1}{1+\sum_{j=1}^k\gamma_j} + \dfrac{1}{2^n}\, \dfrac{1}{1+\sum_{j=1}^n \gamma_j} }_{\,=\!:\, D_i} \Bigg), \end{aligned} \end{equation}
in which to go from the second to the third line of (B.11), recombine terms by adding all the factors of
$\gamma_i$
. We follow the convention that the sum is zero whenever the lower index exceeds the upper index.
Next, we show that the
$i{\rm th}$
term on the left side of (B.9) is greater than the
$i{\rm th}$
term of (B.11), for
$i = 1, 2, \dots, n$
. To see this, consider function
$f(x) = x +1 - \sqrt{x^2+1}$
, which increases from 0 to 1 as x increases from 0 to
$\infty$
. Therefore, for a given constant
$c \in (0, 1)$
,
$f(x) > c$
if and only if
$x > f^{-1}(c) = \frac{c(2-c)}{2(1-c)}$
. Set
$c = 2\gamma_i D_i$
(which is less than 1); thus, we wish to show
\[\dfrac{\hat{\phi}_0}{\varepsilon_i} > \dfrac{\gamma_iD_i(2 - 2\gamma_iD_i)}{1 - 2\gamma_iD_i}.\]
From
$\frac{\hat{\phi}_0}{\varepsilon_i} = \gamma_i \frac{\hat{\phi}_0}{\varepsilon_0}$
and (B.10), this inequality is equivalent to
\[\gamma_i \Bigg( \dfrac{1}{2} + \sum_{k=1}^{i-1} \dfrac{1}{2^{k+1}} \, \dfrac{1}{1+\sum_{j=1}^k \gamma_j} + D_i \Bigg) > \dfrac{2 \gamma_iD_i(1 - \gamma_iD_i)}{1 - 2\gamma_iD_i},\]
or
\[\dfrac{1}{2} + \sum_{k=1}^{i-1} \dfrac{1}{2^{k+1}} \, \dfrac{1}{1+\sum_{j=1}^k \gamma_j} > \dfrac{D_i}{1-2\gamma_iD_i},\]
which is true because
\[2(1+\gamma_i)D_i < 2 \left(\sum_{k=i}^{n-1} \dfrac{1}{2^{k+1}} + \dfrac{1}{2^n} \right) = \dfrac{1}{2^{i-1}} \le 1,\]
which implies
$\frac{D_i}{1-2\gamma_i D_i} < \frac{1}{2}$
. This completes the proof.
Open access
