Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:58:04.563Z Has data issue: false hasContentIssue false
  • English
  • Français

The Performance of Alternative Models for Forecasting Automobile Insurance Paid Claim Costs

Published online by Cambridge University Press:  29 August 2014

J. David Cummins  and
Alwyn Powell
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When setting or modifying insurance rates on the basis of observed data, adjustments should be made for inflation between the average claim date of the observation period and the average claim date covered by policies to which the new rates will apply. In automobile insurance ratemaking in the United States, the adjustment is made as follows:

where Lα = trended losses and loss adjustment expenses incurred,

L0 = observed losses and loss adjustment expenses incurred during the experience period,

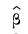= the predicted rate of inflation per quarter, and

k = the number of quarters for which losses are being trended.

The inflation coefficient, β, is an exponential growth factor that is estimated using the following equation:

where 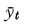= average paid claim costs for the year ending in quarter t,

t = time, in quarters, t = 1, 2, …, 12, and

εt = a random disturbance term.

The estimation period for the equation is the twelve quarters immediately preceding the first forecast period, and the estimation is conducted utilizing ordinary least squares. Annual averages of claim costs are used as the dependent variable to smooth random and seasonal fluctuations.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 11 , Issue 2 , December 1980 , pp. 91 - 106
Copyright
Copyright © International Actuarial Association 1980

References

REFERENCES

Cook, C. (1970). Trend and Loss Development Factors, Proceedings of the Casualty Actuarial Society, 52, 1–14.Google Scholar
Durbin, J. (May 1970). Testing for Serial Correlation in Least-Squares Regression When Some of the Regressors Are Lagged Dependent Variables, Econometrica, 38, no. 3, 410–421.CrossRefGoogle Scholar
Glejser, H. (1969). A New Test for Heteroskedasticity, Journal of the American Statistical Association, 64, 316–323.CrossRefGoogle Scholar
Goldfeld, S. M. and Quandt, R. E. (1965). Some Tests for Homoskedasticity, Journal of the American Statistical Association, 60, 539–547.CrossRefGoogle Scholar
Hall, B., Hall, R., and Becketti, S. (1977). Time Series Processor, Version 3.5, Privately published. Stanford, Calif.Google Scholar
Harrison, M. J. and McCabe, B. P. M. (1979). A Test for Heteroskedasticity Based on Ordinary Least Squares Residuals, Journal of the American Statistical Association, 74, 494–499.Google Scholar
Harvey, A. C. and Phillips, G. D. A. (1974). A Comparison of the Power of Some Tests for Heteroskedasticity in the General Linear Model, Journal of Econometrics, 2, 307–316.CrossRefGoogle Scholar
Klein, L. R. and Burmeister, E. (1976). Econometric Model Performance: Comparative Simulation Studies of the U.S. Economy, University of Pennsylvania Press, Philadelphia.CrossRefGoogle Scholar
Kmenta, J. (1971). Elements of Econometrics, The Macmillan Co., New York.Google Scholar
Spencer, B. G. (1975). The Small Sample Bias of Durbin's Test for Serial Correlation, Journal of Econometrics, 3, 249–254.CrossRefGoogle Scholar
Waelbroeck, J., ed. (1976). The Models of Project LINK, North-Holland Publishing Co., Amsterdam.Google Scholar