Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T13:36:11.619Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Use of Extreme Values to Estimate the Premium for an Excess of Loss Reinsurance

Published online by Cambridge University Press:  29 August 2014

Jan Jung
Jan Jung*
Affiliation:
Stockholm, Sweden
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

I. Suppose that the claims experienced by a portfolio could be represented as independent random variables with a distribution function F(x). The net premium per claim for an excess loss cover above an amount of L is then

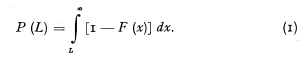
If we have no information about F(x) except a number M of independent claims, we might compute the observed “staircase” distribution function SM (x) which is for every x an unbiased estimate of F(x), and could thus compute an unbiased estimate for P(L) with the variance [7])

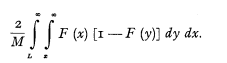
2. In real life we have some qualitative knowledge of F(x) and very limited information about the claims. In his introduction to this subject Beard treats the case where the only information about F(x) consists of the largest claim xi and the number of claims ni (i = 1, 2, …, N) observed during N periods (Reference No 2). It is known from the theory of extreme values [3] that for large ni the distribution of xi depends mainly on the parameters uni and αni( defined by

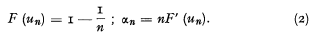
Beard further assumes that F(x) belongs to what is called by Gumbel “the exponential type” of distribution functions, which have an unlimited tail and finite moments. This class is strictly defined by Gnedenko's necessary and sufficient condition [4, p. 68]:

Type
Papers
Information
ASTIN Bulletin: The Journal of the IAA , Volume 3 , Issue 2 , August 1964 , pp. 178 - 184
Copyright
Copyright © International Actuarial Association 1964

References

REFERENCES

[1]Beard, R. E.: “Statistical Theory of Extreme Values and an Application to Excess of Loss Reinsurance.” (Mimeographed MS 1962).Google Scholar
[2]Beard, R. E.: “4th ASTIN Colloquium: Subjects for discussion.” The ASTIN Bulletin, Vol. II, part III, p. 313, 1963.Google Scholar
[3]Gumbel, E. J.: “Statistics of Extremes”. Columbia Un. Press. N.Y. 1958.CrossRefGoogle Scholar
[4]Sarhan, A. E. and Greenberg, B. G.: “Contributions to Order Statistics”. Wiley, London and N.Y. 1962.Google Scholar
[5]Franckx, Ed.: “Sur la fonction de distribution du sinistre le plus elevé”. The ASTIN Bulletin, Vol. II, part III, 1963.Google Scholar
[6]Hamlet, : Monologue on decision theory. Laggard and Blount, 1623.Google Scholar
[7]Vajda, S.: “Analytical Studies in Stop-Loss Reinsurance”. Skand. Akt. 1951, P. 158.Google Scholar