In many risk theoretical questions a central problem is the numerical evaluation of a convolution integral and much effort has been devoted over the years to mathematical and computational aspects. The paper presented to this colloquium by O. Thorin shows the subject to be topical but the present note stems from a recent paper by H. L. Seal, “Simulation of the ruin potential of non-life insurance companies”, published in the Transactions of the Society of Actuaries, Volume XXI page 563.

In this paper, amongst other topics, Seal has presented some simulations of ruin probabilities over a finite time interval. Some years ago (Journal Institute of Actuaries Students' Society, Volume 15, 1959). I pointed out that the form of ruin probability could be expressed as a successive product of values of a distribution function. To my knowledge no one has attempted to see if this product form was capable of development and the numerical values in Seal's paper prompted me to spend a little time on the problem. In the time I had available it has not been possible to do more than experiment, but the conclusions reached may be of interest to other workers in this field. They showed that calculation is feasible but laborious. However, the knowledge that it can be done may suggest methods of improving the techniques.

Seal's first simulation example is the calculation of ruin probabilities when the distribution of the interval of time between the claims is negative exponential and the individual claim distribution is also negative exponential. Instead of following Seal's method we can determine the “gain per interval” and find that if λ is the security loading the frequency function for the gain z is

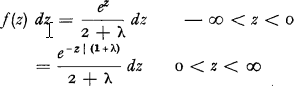
i.e. a Laplace distribution.